遞歸最小二乘循環神經網絡

趙 杰 張春元 劉 超 周 輝 歐宜貴 宋 淇

循環神經網絡(Recurrent neural networks,RNNs)作為一種有效的深度學習模型,引入了數據在時序上的短期記憶依賴.近年來,RNNs 在語言模型[1]、機器翻譯[2]、語音識別[3]等序列任務中均有不俗的表現.但是相比前饋神經網絡而言,也正因為其短期記憶依賴,RNNs 的參數訓練更為困難[4-5].如何高效訓練RNNs,即RNNs 的優化,是RNNs能否得以有效利用的關鍵問題之一.目前主流的RNNs 優化算法主要有一階梯度下降算法、自適應學習率算法和二階梯度下降算法等幾種類型.

最典型的一階梯度下降算法是隨機梯度下降(Stochastic gradient descent,SGD)[6],廣泛應用于優化RNNs.SGD 基于小批量數據的平均梯度對參數進行優化.因為SGD 的梯度下降大小和方向完全依賴當前批次數據,容易陷入局部極小點,故而學習效率較低,更新不穩定.為此,研究者在SGD的基礎上引入了速度的概念來加速學習過程,這種算法稱為基于動量的SGD 算法[7],簡稱為Momentum.在此基礎上,Sutskever 等[8]提出了一種Nesterov 動量算法.與Momentum 的區別體現在梯度計算上.一階梯度下降算法的超參數通常是預先固定設置的,一個不好的設置可能會導致模型訓練速度低下,甚至完全無法訓練.針對SGD 的問題,研究者提出了一系列學習率可自適應調整的一階梯度下降算法,簡稱自適應學習率算法.Duchi 等[9]提出的AdaGrad 算法采用累加平方梯度對學習率進行動態調整,在凸優化問題中表現較好,但在深度神經網絡中會導致學習率減小過快.Tieleman 等[10]提出的RMSProp 算法與Zeiler[11]提出的AdaDelta算法在思路上類似,都是使用指數衰減平均來減少太久遠梯度的影響,解決了AdaGrad學習率減少過快的問題.Kingma 等[12]提出的Adam 算法則將RMSProp 與動量思想相結合,綜合考慮梯度的一階矩和二階矩估計計算學習率,在大部分實驗中比AdaDelta 等算法表現更為優異,然而Keskar 等[13]發現Adam 最終收斂效果比SGD 差,Reddi 等[14]也指出Adam 在某些情況下不收斂.

基于二階梯度下降的算法采用目標函數的二階梯度信息對參數優化.最廣泛使用的是牛頓法,其基于二階泰勒級數展開來最小化目標函數,收斂速度比一階梯度算法快很多,但是每次迭代都需要計算Hessian 矩陣以及該矩陣的逆,計算復雜度非常高.近年來研究人員提出了一些近似算法以降低計算成本.Hessian-Free 算法[15]通過直接計算Hessian 矩陣和向量的乘積來降低其計算復雜度,但是該算法每次更新參數需要進行上百次線性共軛梯度迭代.AdaQN[16]在每個迭代周期中要求一個兩層循環遞歸,因此計算量依然較大.K-FAC 算法(Kronecker-factored approximate curvature)[17]通過在線構造Fisher 信息矩陣的可逆近似來計算二階梯度.此外,還有BFGS 算法[18]以及其衍生算法(例如L-BFGS 算法[19-20]等),它們都通過避免計算Hessian 矩陣的逆來降低計算復雜度.相對于一階優化算法來說,二階優化算法計算量依然過大,因此不適合處理規模過大的數據集,并且所求得的高精度解對模型的泛化能力提升有限,甚至有時會影響泛化,因此二階梯度優化算法目前還難以廣泛用于訓練RNNs.

除了上面介紹的幾種類型優化算法之外,也有不少研究者嘗試將遞歸最小二乘算法(Recursive least squares,RLS)應用于訓練各種神經網絡.RLS 是一種自適應濾波算法,具有非常快的收斂速度.Azimi-Sadjadi 等[21]提出了一種RLS 算法,對多層感知機進行訓練.譚永紅[22]將神經網絡層分為線性輸入層與非線性激活層,對非線性激活層的反傳誤差進行近似,并使用RLS 算法對線性輸入層的參數矩陣進行求解來加快模型收斂.Xu 等[23]成功將RLS 算法應用于多層RNNs.上述算法需要為每個神經元存儲一個協方差矩陣,時空開銷很大.Peter等[24]提出了一種擴展卡爾曼濾波優化算法,對RNNs 進行訓練.該算法將RNNs 表示為被噪聲破壞的平穩過程,然后對網絡的狀態矩陣進行求解.該算法不足之處是需要計算雅可比矩陣來達到線性化的目的,時空開銷也很大.Jaeger[25]通過將非線性系統近似為線性系統,實現了回聲狀態網絡參數的RLS 求解,但該算法僅限于求解回聲狀態網絡的輸出層參數,并不適用于一般的RNNs 訓練優化.

針對以上問題,本文提出了一種新的基于RLS優化的RNN 算法(簡稱RLS-RNN).本文主要貢獻如下:1)在RLS-RNN 的輸出層參數更新推導中,借鑒SGD 中平均梯度的計算思想,提出了一種適于迷你批樣本訓練的RLS 更新方法,顯著減少了RNNs 的實際訓練時間,使得所提算法可處理較大規模數據集.2)在RLS-RNN 的隱藏層參數更新推導中,提出了一種等效梯度思想,以獲得該層參數的最小二乘解,同時使得RNNs 僅要求輸出層激活函數存在反函數即可采用RLS 進行訓練,對隱藏層的激活函數則無此要求.3)相較以前的RLS優化算法,RLS-RNN 只需在隱藏層和輸出層而非為這兩層的每一個神經元分別設置一個協方差矩陣,使得其時間和空間復雜度僅約SGD 算法的3 倍.4)對RLS-RNN 的遺忘因子自適應和過擬合預防問題進行了簡要討論,分別給出了一種解決辦法.

1 背景

1.1 基于SGD 優化的RNN 算法

RNNs 處理時序數據的模型結構如圖1 所示.一個基本的RNN 通常由一個輸入層、一個隱藏層(也稱為循環層)和一個輸出層組成.在圖1 中,Xs,t∈Rm×a,Hs,t∈Rm×h和Os,t∈Rm×d分別為第s批訓練樣本數據在第t時刻的輸入值、隱藏層和輸出層的輸出值,其中,m為迷你批大小,a為一個訓練樣本數據的維度,h為隱藏層神經元數,d為輸出層神經元數;Us-1∈Ra×h,Ws-1∈Rh×h和Vs-1∈Rh×d分別為第s批數據訓練時輸入層到隱藏層、隱藏層內部、隱藏層到輸出層的參數矩陣;∈R1×h和∈R1×d分別為隱藏層和輸出層的偏置參數矩陣;τ表示當前序列數據共有τ時間步.RNNs 的核心思想是在模型的不同時間步對參數進行共享,將每一時間步的隱藏層輸出值加權輸入到其下一時間步的計算中,從而令權重參數學習到序列數據不同時間步之間的關聯特征并進行泛化.輸出層則根據實際問題選擇將哪些時間步輸出,比較常見的有序列數據的分類問題和預測問題.對序列數據預測問題,輸出層每一時間步均有輸出;對序列數據分類問題,輸出層沒有圖1 虛線框中的時間步輸出,即僅在最后一個時間步才有輸出.

圖1 RNN 模型結構Fig.1 RNN model structure

RNNs 通過前向傳播來獲得實際輸出,其計算過程可描述為

其中,1 為m行全1 列向量;φ(·) 和σ(·)分別為隱藏層和輸出層的激活函數,常用的激活函數有sigmoid 函數與tanh 函數等.為了便于后續推導和表達的簡潔性,以上兩式可用增廣矩陣進一步表示為

RNNs 的參數更新方式和所采用的優化算法密切相關,基于SGD 算法的RNNs 模型優化通常借助于最小化目標函數反向傳播完成.常用目標函數有交叉熵函數、均方誤差函數、Logistic 函數等.這里僅考慮均方誤差目標函數

式中,?為Hadamard 積,為輸出層非激活線性輸出,即

則該層參數更新規則可定義為

其中,α為學習率.

則該層參數更新規則可定義為

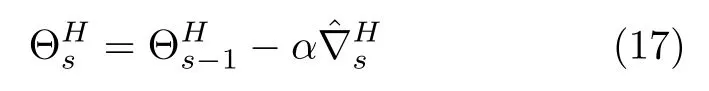
1.2 RLS 算法

RLS 是一種最小二乘優化算法的遞推化算法,不但收斂速度很快,而且適用于在線學習.設當前訓練樣本輸入集Xt={x1,···,xt},對應的期望輸出集為.其目標函數通常定義為

其中,w為權重向量;λ∈(0, 1] 為遺忘因子.

令?wJ(w)=0,可得

整理后可表示為

其中,

為了避免昂貴的矩陣求逆運算且適用于在線學習,令

將式(21)和式(22)改寫為如下遞推更新形式

由Sherman-Morrison-Woodbury 公式[27]易得

其中,

其中,gt為增益向量.進一步將式(23)、(25)和(26)代入式(20),可得當前權重向量的更新公式為

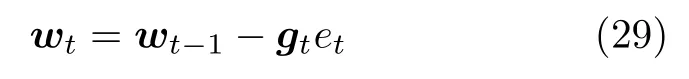
其中,

2 基于RLS 優化的RNNs 算法

RLS 算法雖然具有很快的學習速度,然而只適用于線性系統.我們注意到在RNNs 中,如果不考慮激活函數,其隱藏層和輸出層的輸出計算依舊是線性的,本節將基于這一特性來構建新的迷你批RLS 優化算法.假定輸出層激活函數σ(·)存在反函數σ-1(·),并仿照RLS 算法將輸出層目標函數定義為

其中,s代表共有s批訓練樣本;為輸出層的非激活線性期望值,即

因此,RNNs 參數優化問題可以定義為

由于RNNs 前向傳播并不涉及權重參數更新,因此本文所提算法應用于RNNs 訓練時,其前向傳播計算與第1.1 節介紹的SGD-RNN 算法基本相同,Hs,t同樣采用式(3)計算,唯一區別是此處并不需要計算Os,t,而是采用式(12)計算.本節將只考慮RLS-RNN 的輸出層和隱藏層參數更新推導.

2.1 RLS-RNN 輸出層參數更新推導

將式(35)代入式(36),得

類似于RLS 算法推導,以上兩式可進一步寫成如下遞推形式

2.2 RLS-RNN 隱藏層參數更新推導

其中,η為比例因子.理論上講,不同迷你批數據對應的η應該有一定的差別.但考慮到各批迷你批數據均是從整個訓練集中隨機選取,因此可忽略這一差別.根據式(16)可知,且將式(59)代入式(55),得

其中,

式(61)的遞歸最小二乘解推導過程類似于輸出層參數更新推導.令,同樣采用上文的近似平均求解方法,易得

綜上,RLS-RNN 算法如算法 1 所示.

3 分析與改進

3.1 復雜度分析

在RNNs 當前所用優化算法中,SGD 是時間和空間復雜度最低的算法.本節將以SGD-RNN 為參照,來對比分析本文提出的RLS-RNN算法的時間和空間復雜度.兩個算法采用一個迷你批樣本數據集學習的時間和空間復雜度對比結果如表1 所示.從第1 節介紹可知,τ表示序列數據時間步長度,m表示批大小,a表示單個樣本向量的維度,h表示隱藏層神經元數量,d表示輸出層神經元數量.在實際應用中,a和d一般要小于h,因而RLS-RNN的時間復雜度和空間復雜度大約為SGD-RNN 的3 倍.在實際運行中,我們發現RLS-RNN 所用時間和內存空間大約是SGD-RNN 的3 倍,與本節理論分析結果正好相吻合.

表1 SGD-RNN 與RLS-RNN 復雜度分析Table 1 Complexity analysis of SGD-RNN and RLS-RNN

所提算法只需在RNNs 的隱藏層和輸出層各設置一個矩陣,而以前的RLS 優化算法則需為RNNs 隱藏層和輸出層的每一個神經元設置一個與所提算法相同規模的協方差矩陣,因而所提算法在時間和空間復雜度上有著大幅降低.此外,所提算法采用了深度學習廣為使用的迷你批訓練方式,使得其可用于處理較大規模的數據集.

3.2 λ 自適應調整

眾多研究表明,遺忘因子λ的取值對RLS 算法性能影響較大[28],特別是在RLS 處理時變任務時影響更大.由于本文所提算法建立在傳統RLS 基礎之上,因而RLS-RNN 的收斂質量也易受λ的取值影響.在RLS 研究領域,當前已有不少關于λ自適應調整方面的成果[28-29],因此可以直接利用這些成果對RLS-RNN 作進一步改進.

在文獻[29]基礎上,本小節直接給出一種λ自適應調整方法.對第s迷你批樣本,RLS-RNN 各層中的遺忘因子統一定義為

其中,λmax接近于1,κ＞1 用于控制λs更新,一般建議取2,通常κ取值越小,λs更新越頻繁;ξ是一個極小的常數,防止在計算λs時分母為0;qs,和定義為

其中,μ0建議取 7/8;μ1=1－1/(?1m),通常?1≥2;μ2=1－1/(?2m),且?2＞?1.

當然,采用以上方式更新λs將會引入新的超參數,給RLS-RNN 的調試帶來一定困難.從使用RLS-RNN 的實際經驗來看,也可采用固定的λ進行訓練,建議將λ取值設置在0.99 至1 之間.

3.3 過擬合預防

傳統RLS 算法雖然具有很快的收斂速度,但也經常面臨過擬合風險,RLS-RNN 同樣面臨這一風險.類似于第3.2 節,同樣可以利用RLS 領域關于這一問題的一些研究成果來改進RLS-RNN.

Ek?io?lu[30]提出了一種L1正則化RLS 方法,即在參數更新時附加一個正則化項.對其稍加改進,則在式(50)和式(65)的基礎上可分別重新定義為

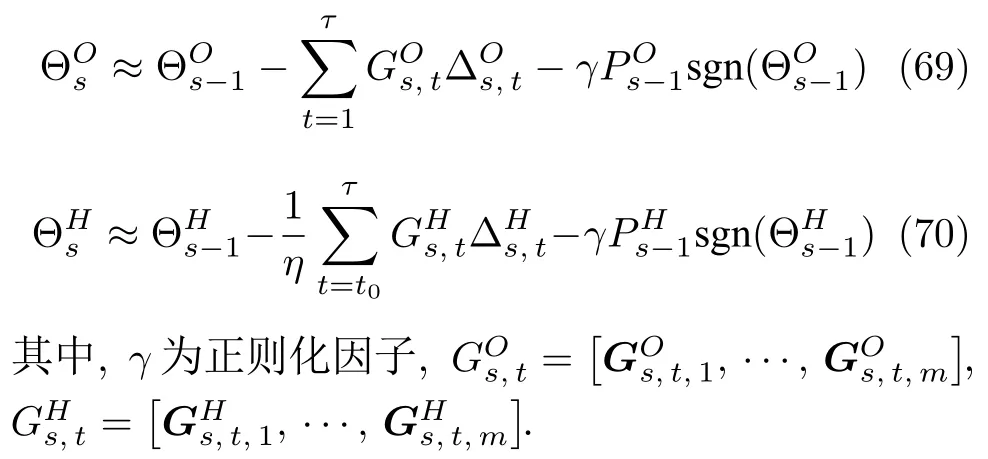
實際上,除了這種方法外,讀者也可采用其他正則化方法對RLS-RNN 作進一步改進.

4 仿真實驗

為了驗證所提算法的有效性,本節選用兩個序列數據分類問題和兩個序列數據預測問題進行仿真實驗.其中,兩個分類問題為MNIST 手寫數字識別分類[31]和IMDB 影評正負情感分類,兩個預測問題為Google 股票價格預測[32]與北京市PM2.5 污染預測[33].在實驗中,將著重驗證所提算法的收斂性能、超參數α和η選取的魯棒性.在收斂性能驗證中,選用主流一階梯度優化算法SGD、Momentum和Adam 進行對比,所有問題的實驗均迭代運行150 Epochs;在超參數魯棒性驗證中,考慮到所提算法收斂速度非常快,所有問題的實驗均只迭代運行50 Epochs.為了減少實驗結果的隨機性,所有實驗均重復運行5 次然后取平均值展示結果.此外,為了觀察所提算法的實際效果,所有優化算法在RNNs 參數更新過程均不進行Dropout 處理.需要特別說明的是:對前兩個分類問題,由于時變性不強,所提算法遺忘因子采用固定值方式而不采用第3.2節所提方式;對后兩個預測問題,所提算法遺忘因子將采用第3.2 節所提方式;所提算法對4 個問題均將采用第3.3 節所提方法防止過擬合.

4.1 MNIST 手寫數字識別分類

MNIST 分類問題的訓練集與測試集分別由55 000和10 000 幅 28×28 像素、共10 類灰度手寫數字圖片組成,學習目標是能對給定手寫數字圖片進行識別.為了適應RNNs 學習,將訓練集和測試集中的每張圖片轉換成一個28 時間步的序列,每時間步包括28 個像素輸入,圖片類別采用One-hot 編碼.

該問題所用RNN 模型結構設置如下:1)輸入層輸入時間步為28,輸入向量維度為28.2)隱藏層時間步為28,神經元數為100,激活函數為tanh(·).3)輸出層時間步為1,神經元數為10,激活函數為tanh(·).由于 tanh-1(1)和 tanh-1(－1)分別為正、負無窮大,在具體實現中,對 tanh-1(x),我們約定:若x≥0.997,則 tanh-1(x)=tanh-1(0.997);若x≤－0.997,則 tanh-1(x)=tanh-1(－0.997).RNN 模型權重參數采用He 初始化[34].

在收斂性能對比驗證中,各優化算法超參數設置如下:RLS 遺忘因子λ為0.9999,比例因子η為1,協方差矩陣初始化參數α為0.4,正則化因子γ為0.0001;SGD 學習率為0.05;Momentum 學習率為0.05,動量參數0.5;Adam 學習率0.001,β1設為0.9,β2為0.999,?設為 10-8.在超參數α和η選取的魯棒性驗證中,采用控制變量法進行測試:1)固定λ=0.9999,γ=0.0001 和η=1,依次選取α=0.01,0.1,0.2,···,1 驗證;2)固定λ=0.9999,γ=0.0001和α=0.4,依次選取η=0.1,1,2,···,10 驗證.

在上述設定下,每一Epoch 均將訓練集隨機劃分成550 個迷你批,批大小為100.每訓練完一個Epoch,便從測試集中隨機生成50 個迷你批進行測試,統計其平均分類準確率.實驗結果如圖2(a)、表2 和表3 所示.由圖2(a)可知,RLS 在第1 個Epoch 便可將分類準確率提高到95%以上,其收斂速度遠高于其他三種優化算法,且RLS 的準確率曲線比較平滑,說明參數收斂比較穩定.表2 和表3記錄了該實驗取不同的α和η時第50 Epoch 的平均分類準確率.從表2 中不難看出,不同初始化因子α在第50 Epoch 的準確率都在97.10%到97.70%之間波動,整體來說比較穩定,說明α對算法性能影響較小.從表3 中可知,不同η取值的準確率均在97.04%到97.80%之間,波動較小,η取值對算法性能的影響也不大.綜上,RLS 算法的α和η取值均具有較好的魯棒性.

圖2 收斂性比較實驗結果Fig.2 Experimental results on the convergence comparisons

表2 初始化因子 α 魯棒性分析Table 2 Robustness analysis of the initializing factor α

表3 比例因子 η 魯棒性分析Table 3 Robustness analysis of the scaling factor η

4.2 IMDB 影評情感分類

IMDB 分類問題的訓練集和測試集分別由25 000和10 000 條電影評論組成,正負情感評論各占50%,學習目標是能對給定評論的感情傾向進行識別.為了適應RNNs 學習,首先從Keras 內置數據集加載訓練集和測試集的各條評論,選取每條評論前32個有效詞構成一個時間步序列,然后對該評論中的每個有效詞以GloVe.6B 預訓練模型[35]進行詞嵌入,使得每個時間步包括50 個輸入維度,評論的正負情感類別采用One-hot 編碼.

該問題所用RNN 模型結構設置如下:1)輸入層輸入時間步為32,輸入向量維度為50.2)隱藏層時間步為32,神經元數為100,激活函數為 tanh(·).3)輸出層時間步為1,神經元數為2,激活函數為tanh(·).tanh-1(x)問題和RNN 模型權重參數的初始化按第4.1 節方式同樣處理.

在收斂性能對比驗證中,各優化算法超參數設置如下:RLS 遺忘因子λ為0.9999,比例因子η為1,協方差矩陣初始化參數α為0.4,正則化因子γ為0.001;SGD 學習率為0.05;Momentum 學習率為0.05,動量參數0.5;Adam 學習率0.0001,β1設為0.9,β2設為0.999,?設為 10-8.在超參數α和η選取的魯棒性驗證中,同樣采用控制變量法進行測試:1)固定λ=0.9999,γ=0.001 和η=1,依次選取α=0.01,0.1,0.2,···,1 驗證;2)固定λ=0.9999,γ=0.001 和α=0.4,依次選取η=0.1,1,2,···,10驗證.

在上述設定下,每一Epoch 均將訓練集隨機劃分成250 個迷你批,批大小為100.每訓練完一個Epoch,便從測試集中隨機生成50 個迷你批進行測試,統計其平均分類準確率.實驗結果如圖2(b)、表2 和表3 所示.由圖2(b)可知,SGD 與Momentum 的收斂不太穩定,波動比較大,而Adam的準確率曲線則比較平滑,這三者在訓練初期的準確率都比較低.相比之下,RLS 在訓練初期的準確率已經比較接近后期預測準確率,前期收斂速度極快,整體準確率也明顯優于其余三種優化算法.表2和表3 記錄了IMDB 實驗取不同的α和η時第50 Epoch 的平均分類準確率.由表2 易知不同α的情況下準確率浮動范圍比較小,因此不同α對算法的影響比較小.由表3 可知,采用不同η時其準確率在72.86%到73.82%之間浮動,可見η的取值對算法性能影響較小.綜上,RLS 算法的α和η取值在本實驗中同樣都具有較好的魯棒性.

4.3 Google 股票價格預測

Google 股票價格預測問題的數據源自Google公司從2010 年1 月4 日到2016 年12 月30 日的股價記錄,每日股價記錄包括當日開盤價、當日最低價、當日最高價、交易筆數及當日調整后收盤價五種數值,學習目標是能根據當日股價預測調整后次日收盤價.為了適應RNNs 學習,首先對這些數值進行歸一化處理,然后以連續50 個交易日為單位進行采樣,每次采樣生成一條5 維輸入序列數據,同時將該次采樣后推一個交易日選取各日調整后收盤價生成對應的一維期望輸出序列數據,取前1 400條序列數據的訓練集,后續200 條序列數據為測試集,并將訓練集和測試集的樣本分別隨機置亂.

該問題所用RNN 模型結構設置如下:1)輸入層輸入時間步為50,輸入向量維度為5.2)隱藏層時間步為50,神經元數為50,激活函數為 tanh(·).3)輸出層時間步為50,神經元數為1,激活函數為identity(·).RNN 模型權重參數采用高斯分布隨機初始化.

在收斂性能對比驗證中,各優化算法超參數設置如下:RLS 遺忘因子采用第3.2 節自適應方式,其參數κ=1.5,λmax=0.9999,q0=10,μ0=7/8,?1=6,?2=18,ξ=10-15,魯棒性實驗中自適應參數與此相同,RLS 的比例因子η為1,協方差矩陣初始化參數α為0.3,正則化因子γ為0.000001;SGD 學習率為0.05;Momentum 學習率為0.05,動量參數0.8;Adam 學習率0.001,β1設為0.9,β2設為0.999,?設為 10-8.在超參數α和η選取的魯棒性驗證中,采用控制變量法進行測試:1)固定γ=0.000001 和η=1,依次選取α=0.01,0.1,0.2,···,1驗證;2)固定γ=0.000001 和α=0.3,依次選取η=0.1,1,2,···,10驗證.

在上述設定下,每一Epoch 均將訓練集隨機劃分成28 個迷你批,批大小為50.每訓練完一個Epoch,便從測試集中隨機生成50 個迷你批進行測試,統計其均方誤差(mean square error,MSE).實驗結果如圖2(c)、表2 和表3 所示.由圖2(c)可知,Adam 在前期誤差較大,但是很快降低到SGD 與Momentum 的誤差之下,Momentum 則比SGD 稍強一些,RLS 則在迭代初期就幾乎收斂.表2 和表3記錄了該實驗取不同的α和η時在第50 Epoch 的平均MSE.由表2 可知,在不同α取值下,實驗結果都比較接近,波動較小,這說明α的取值對于RLS 算法性能的影響較小.由表3 可知,當η取不同值時,MSE 值變化不大,因此η對算法影響較小.綜上,RLS 算法的α和η取值在本實驗中也具有較好的魯棒性.

4.4 北京市PM2.5 污染預測

北京市PM2.5 污染預測問題的數據源自2010年1 月1 日至2014 年12 月31 日每小時的監測記錄.每條記錄由PM2.5 濃度、露點、攝氏溫度、氣壓、組合風向、累計風速、降雪量、降水量共8 個屬性值組成,學習目標是能根據當前小時的監測記錄預測兩個小時后的PM2.5 濃度值.為了適應RNNs 學習,首先對風向數據按序編碼,然后對屬性數值歸一化,接著以連續24 小時為單位進行采樣,每次采樣生成一條8 維輸入序列數據,同時將該次采樣后推兩個小時選取各小時的PM2.5 濃度值生成一條對應的一維期望輸出序列數據,并取前35 000 條序列數據為訓練集,后續8 700 條序列數據為測試集.需要說明的是,由于這一問題比較簡單且訓練集較大,所提算法和Adam 運行一個Epoch基本即可收斂,為了更好地對各算法性能進行區分,只取訓練集前7 000 條和測試集前3 700 條數據并分別隨機置亂進行訓練和測試.

該問題所用RNN 模型結構設置如下:1)輸入層輸入時間步為24,輸入向量維度為8.2)隱藏層時間步為24,神經元數為50,激活函數為 tanh(·).3)輸出層時間步為24,神經元數為1,激活函數為identity(·).RNN 模型權重參數的初始化按第4.3 節方式同樣處理.

在收斂性能對比驗證中,各優化算法超參數設置如下:RLS 遺忘因子采用第3.2 節自適應方式,其參數κ=2,λmax=0.9999,q0=10,μ0=7/8,?1=6,?2=18,ξ=10-15,魯棒性實驗中自適應參數與此相同,RLS 的比例因子η為1,協方差矩陣初始化參數α為0.4,正則化因子γ為0.000001;SGD 學習率為0.05;Momentum 學習率為0.05,動量參數0.8;Adam 學習率0.001,β1設為0.9,β2設為0.999,?設為 10-8.在超參數α和η選取的魯棒性驗證中,同樣采用控制變量法進行測試:1)固定γ=0.000001和η=1,依次選取α=0.01,0.1,0.2,···,1驗證;2)固定γ=0.000001 和α=0.4,依次選取η=0.1,1,2,···,10 驗證.

在上述設定下,每一Epoch 均將訓練集隨機劃分成140 個迷你批,批大小為50.每訓練完一個Epoch,便從測試集中隨機生成50 個迷你批進行測試,統計其均方誤差損失.實驗結果如圖2(d)、表2和表3 所示.由圖2(d)可知,SGD、Momentum、Adam 的損失初期均較大,收斂速度較緩慢;而RLS 的曲線幾乎在第1 個Epoch 就收斂完成,因此其收斂速度要優于3 個對比優化算法.表2 和表3記錄了該實驗取不同的α和η時在第50 Epoch的平均MSE.表2 中在取不同α時,其MSE 上下波動幅度較小,且沒有明顯的變化趨勢,因此我們認為α對算法性能影響較小.由表3 可知,對η取不同值時,其平均MSE 在 1.50×10-3到1.59×10-3間波動,整體來說浮動范圍較小.綜上,RLS 算法的α和η取值都具有較好的魯棒性.

5 結論與展望

在RNNs 優化訓練中,現有一階優化算法學習速度較慢,而二階優化算法和以前的RLS 類型優化算法時空復雜度又過高.為此,本文提出了一種新的RLS 優化算法.該算法吸收了深度學習中廣為應用的迷你批訓練學習模式,在推導過程中我們將研究重點放置在隱藏層和輸出層的非激活線性輸出上,通過等價梯度替換,最終得到各層權重參數的遞歸最小二乘解.所提算法只需在RNNs 的隱藏層和輸出層各添加一個協方差矩陣,解決了長期以來RLS 優化算法應用時需要為隱藏層和輸出層的每一神經元設置一個協方差矩陣的問題,極大地降低了時空復雜度,使得RLS 可以適用于較大規模的RNNs 訓練.在此基礎上,采用遺忘因子自適應調整和正則化技術對所提算法作了改進,進一步提高了所提算法的性能.4 組仿真實驗表明,所提算法在收斂性能、穩定性以及超參數選取的魯棒性等方面均要明顯優于主流一階優化算法,能夠有效加快RNNs 模型的訓練速度,降低超參數的選擇難度.此外,在實驗過程中我們還發現所提算法可緩解梯度消失導致RNNs 無法訓練的問題.如何將本算法擴展到RNNs 以外的其他深度學習網絡以及如何進一步降低所提算法的時空復雜度將是我們下一步工作的重點.