Hard-core Hall tube in superconducting circuits
Xin Guan(關欣) Gang Chen(陳剛) Jing Pan(潘婧) and Zhi-Guo Gui(桂志國)
1Department of Materials and Chemical Engineering,Taiyuan University,Taiyuan 030032,China
2State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Laser Spectroscopy,Shanxi University,Taiyuan 030006,China
3Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
4Collaborative Innovation Center of Light Manipulations and Applications,Shandong Normal University,Jinan 250358,China
Keywords: Hall tube,superconducting circuits,topological phase transition,chiral edge currents
1. Introduction
As the forefront of condensed matter physics, topological physics raised enormous attention in the past decades.Topological insulators[1–4]lie at an important position of the researches of topological state, which is beyond Landau symmetry breaking theory and is characterized by topological edge states and topological invariants. An fundamental effect in the topological insulator is the quantum Hall effect[5–9]which is induced by an external magnetic field in two-dimensional system. One of the essential models to investigate the quantum Hall physics is the Hofstader–Harper(H–H) Hamiltonian[10]which has been intensively studied both in theories and experiments.[11–14]In recent cold atom experiments, H–H Hamiltonian was demonstrated both in ladders[15,16]and cylinder[17]systems, dubbed Hall ribbons and Hall tube respectively. These two models were constructed in one dimensional optical lattice with fermion and another dimension was synthetic using the internal degrees of freedom of atoms. Chiral edge currents and topological phase are observed in Hall ribbons and tube respectively. Moreover, the topological insulator emerging in Hall tube breaks the time–reversal,particle–hole,and chiral symmetries simultaneously and is protected by an inversion symmetry,which is same as the integer quantum Hall state.Therefore,Hall tube is the simplest model without using parameter space to simulate the integer quantum Hall effects.
On the other hand, superconducting circuits as a platform with fine tunability, long coherent time and highprecision measurement[18,19]can be used for quantum computation,[20,21]quantum information,[22,23]and quantum simulation.[24–27]Especially, in recent experiments, the topological physics have been investigated in superconducting circuits. Some topological concepts have been studied in parameter[28–31]and phase[32,33]space of superconducting qubits and resonators respectively. Moreover topological magnon insulator[34]has been simulated in single superconducting qubit chain. However the Hall tube as a a minimum model to simulate the integer quantum Hall effects has not been investigated in superconducting circuits which is much easier to construct the tube geometric structure in real space compared with the other artificial systems.
In this paper we propose a scheme to realize the Hall tube with superconducting circuits and explore the topological phase transition in this model. Since the chirality is an essential character of the Hall effect,we investigate the chirality of the Hall tube. We find the topological protected chiral edge currents and discuss its robustness. Finally, we give a feasible experimental scheme to observe the topological state and topological protected chiral edge currents.
2. Hard-core Hall tube in superconducting circuits
Figure 1(a) shows our proposed three-leg superconducting circuits with transmon qubits to realize a hard-core Hall tube with an effective magnetic flux per plaquette. Along each leg, the transmon qubits are coupled with their nearestneighbor sites, while they interact with each other between legs at the same unit cell. All couplers are capacitors.Moreover,there exist both nearest-neighbor and next-nearestneighbor couplings between the transmon qubits which has been realized in experiments.[35,36]The corresponding Lagrangian is written as


To further realize a synthetic Hall tube shown in Fig.1(b),two alternating-current microwave drivings of each transmon qubit are taken into account. These microwave drivings can be achieved experimentally by the flux-bias lines.[38–40]In this case,each qubit frequency is modulated independently as
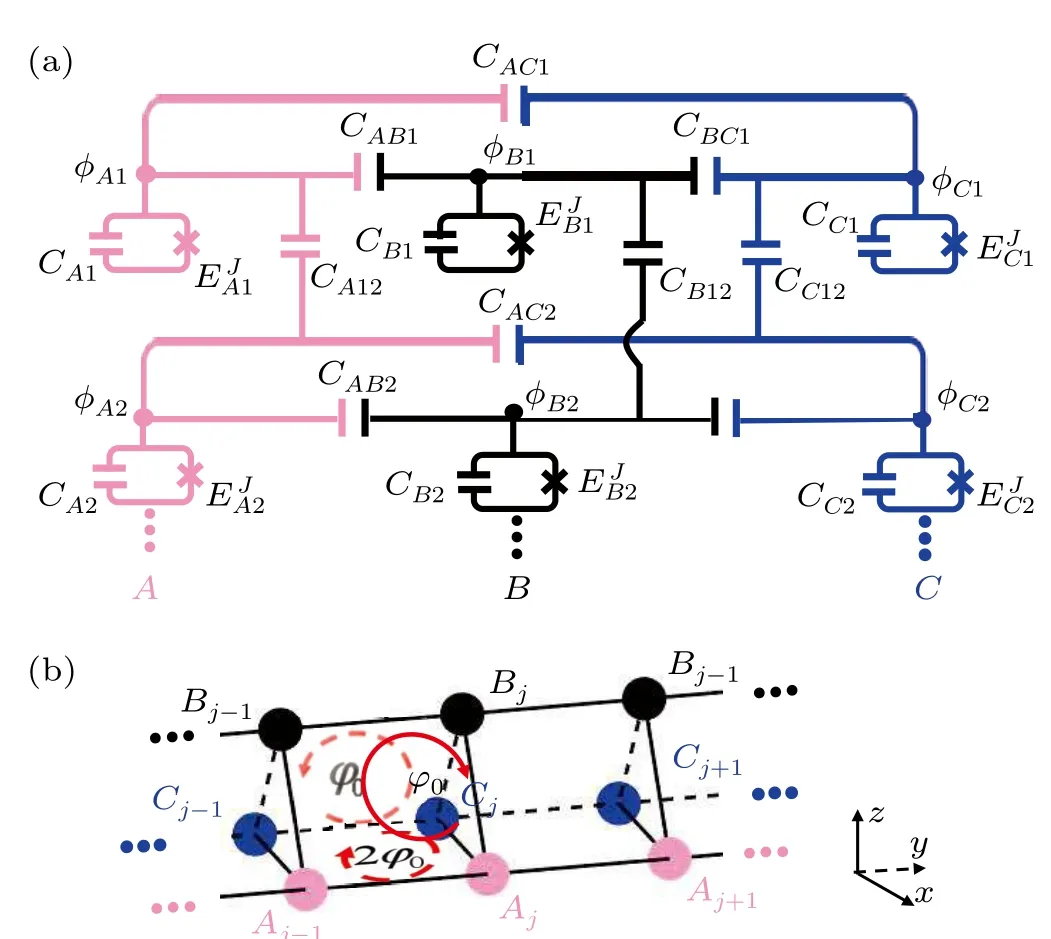
Fig. 1. (a) Three-leg (labeled respectively by A, B, and C) superconducting circuits with transmon qubits. Along each leg, the transmon qubits are coupled with their nearest-neighbor sites,while they interact with each other between legs at the same unit cell. All couplers are capacitors. Cν j and EJν j are the effective capacitance and the Josephson energy of the transmon qubit at the j-th site on the ν-th leg. Cνij and {CABj,CBC j,CCAj} are the capacitors to couple the transmon qubits at the j-th site on the ν-th leg with its nearest-neighbor sites along each leg and between the legs,respectively. φν j is the node flux. (b)Schematics of the hard-core Hall tube with an effective magnetic flux ?0 in the plaquettes A(j?1)AjBjB(j?1) and C(j?1)CjBjB(j?1)and 2?0 in the plaquette A(j?1)AjCjC(j?1). The pink, black, and blue filled circles indicate the transmon qubits in the A,B,and C legs,respectively.
3. Topological property

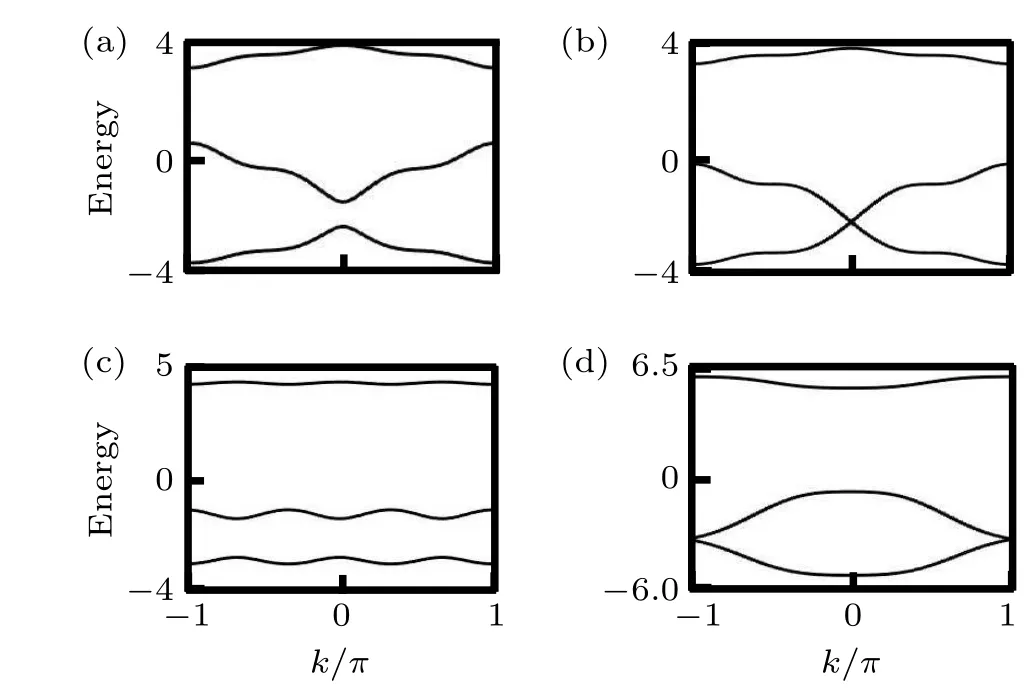
Fig.2. Energy bands as functions of the momentum k with(a)tCA=0.5,(b)tCA =1, (c)tCA =2, and (d)tCA =4. The same parameters are ?0 =2π/3 and ?t=2. Here t0 is used as the unit.
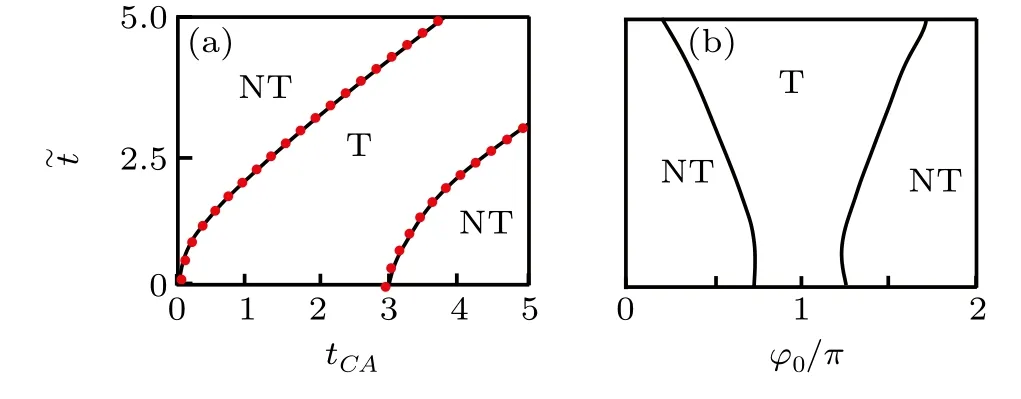
Fig. 3. Topological phase diagram in (a) tCA–?t plane with ?0 =2π/3 and(b) ?0–?t plane with tCA =2. T and NT indicate the topological nontrivial and trivial phases respectively. The black curves and red dots indicate the numerical and analytical results respectively. Here t0 is used as the unit.

whereun(k) denotes the Bloch wavefunction of then-th energy band. FortCA

3.1. Chiral edge currents
Chirality is a hallmark signature for the Hall effect.Based on the chirality, Meissner to vortex phase transition,[50–53]interaction-induced dynamical chiral currents,[54]chiral spin clusters,[55]photonic fractional topological insulators,[56–58]topological superfluid,[59–61]and superconductivity,[62]and moreover high-Tcsuperconductors[63,64]have been investigated. As a minimal model to simulate the integer Hall effect,the chirality of the Hall tube raises much interesting.
Since the Hall tube exhibits nontrivial topology,the chiral edge currents are expected to occur under the edge states.
In the topological nontrivial phase,the densities locate on the edges of the system. The interleg currents are defined as
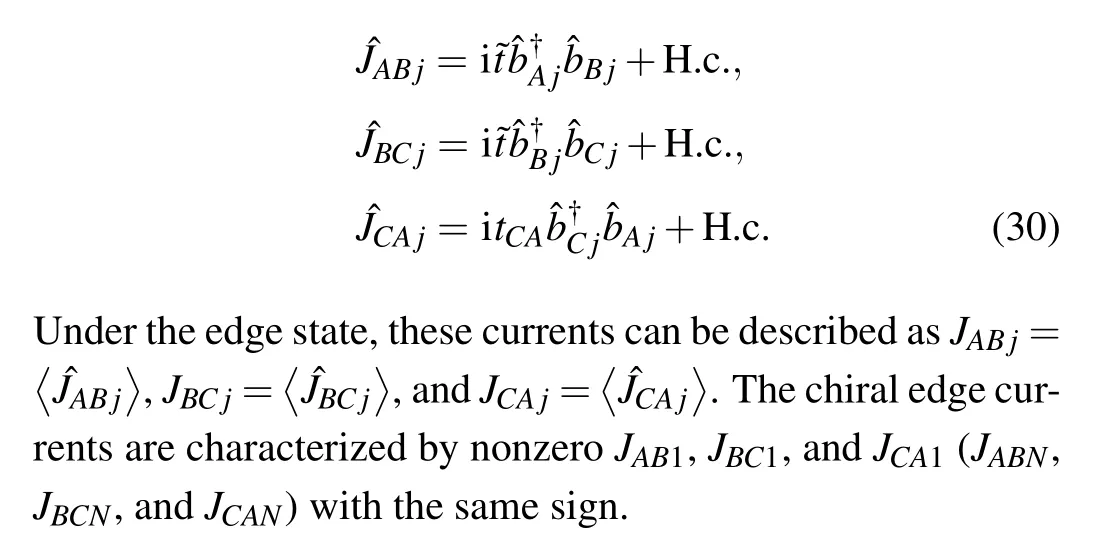
To see the chiral edge currents, we plot the currents and densities distributions in Figs. 4(a) and 4(b) with ?t=tCA=2 under theL-th and (L+1)-th eigen states of the Hamiltonian(18)respectively. It is obviously,the currents located on the edges of the tube have chirality. Moreover the currents under different states have opposite directions, which corresponds with the integer quantum Hall effects in two dimensional system. By numerical calculation, we findJAB1(JBC1)andJBCN(JACN) are always equal, which is also shown in Figs. 4(c) and 4(d). In Figs. 4(c)–4(f) we plot the phase diagrams as functions of ?tandtCA. We can see when ?t=tCA,JAB1,JBC1, andJCA1become nonzero(zero) withJABN,JBCN,andJCANbecome zero (nonzero) respectively, which means the chiral currents only locate on one edge. When ?t ?=tCA,JAB1,JBC1, andJCA1always have opposite values withJABN,JBCN, andJCANrespectively, which indicates the chiral currents have opposite direction between the edges withj=1 andj=N. Moreover,the chiral edge currents are found in the topological nontrivial phase indicated by TC in Fig.4(g).
In the practical experiments,the exact values of the coupling strength can not be tuned. Considering the influence of the imperfections in device fabrication, the imperfection Hamiltonian can be written as
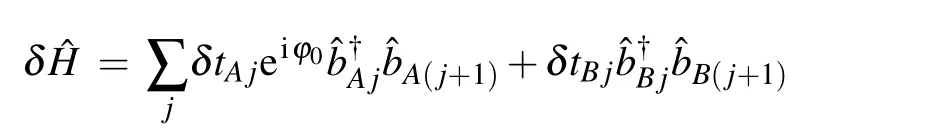
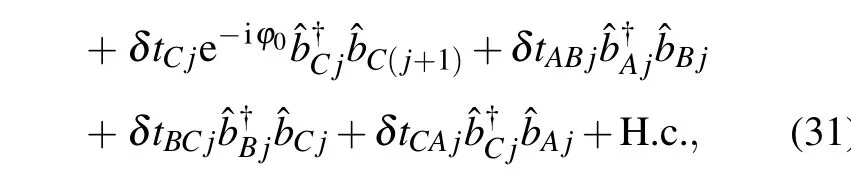
whereδtν jandδtνν′jequal toWδ.Wis the imperfection strength andδ ∈[?0.5,0.5] is a random number. The corresponding imperfection chiral edge currents also with the imperfection hopping strength. We show the imperfection influence of the chiral currents in Fig.4(h). We plot the total edge currentsJE=|JAB1|+|JBC1|+|JCA1|+|JABN|+|JBCN|+|JCAN|as a function of log10Wwith ?t=tCA=2. As log10Wincreasing,JEdecreases slowly in the case of log10W?1,JEsuddenly decreases with log10Wincreasing.This means when the strength of the imperfection is not large enough,the chiral edge currents are robust.
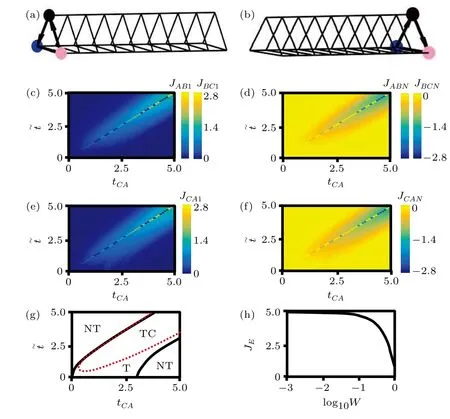
Fig.4. Chiral edge currents and densities distributions on the Hall tube with ?t=tCA=2 under(a)the L-th and(b)(L+1)-th edge states. The thicknesses of the arrows indicate their strengths. The pink,black,and blue filled circles denote the local densities on legs A,B,and C respectively. Phase diagram of(c)JAB1 and JBC1,(d)JABN and JBCN,(e)JCA1,and(f)JCAN as functions of tCA and ?t. (g) Chiral edge currents phase emerging in the topological nontrival phase is indicated by TC.(h)JE as the function of log10W with ?t=tCA=2.The same parameter is ?0=2/3π. Here t0 is used as the unit.
4. Possible experimental observation
In theoretical analysis,for showing the physical phenomena clearly we need consider large size and large parameters interval. While in experiments, to obtain the topological state [Figs. 5(a) and 5(b)] and the corresponding chiral edge currents [Figs. 5(c) and 5(d)] we just need four unit cells and a group fixed parameters. For simplicity we choose the parameters as ?t=tCA=t0. In this case, we just need single alternating-current microwave to drive each qubit, because whenε′ν j= 0,aν j=α,?ν j=uν j(?uν j),?ABj=uB j(?uB j),?BC j=uC j(?uC j), and?CAj=uAj(?uAj) for odd (even)j, all coupling strengths reduce asg0J0(α)J1(α).For obtaining gauge-invariant magnetic flux?0, the phases should be set as ??ν j=(?1)j+1?ν j+π/2, ??ABj=???BAj=(?1)j+1?Bj+π/2, ??BC j=???CBj=(?1)j+1?C j+π/2,and ??CAj=???AC j=(?1)j+1?Aj+π/2 with considering?ν j=(?1)j+1?0j ?π/2.state|ψ〉E, the corresponding density matrix ?ρEcan be constructed by quantum state tomography.[66,67]This means that the chiral edge currents can be obtained by tr(?ρE?Jνν′j) withj=1 or 4.[65]
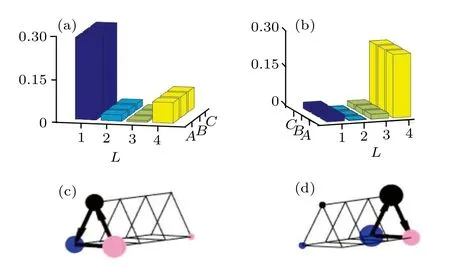
Fig. 5. Densities distributions of the edge states with (a) the L-th and (b)the (L+1)-th wavefunctions. The corresponding chiral edge currents and densities distributions on the Hall tube are shown in panels(c)and(d). The thicknesses of the arrows indicate their strengths. The pink,black,and blue filled circles denote the local densities on legs A,B,and C respectively. The parameters are ?t=tCA=1,?0=2/3π,and L=4. Here t0 is used as the unit.
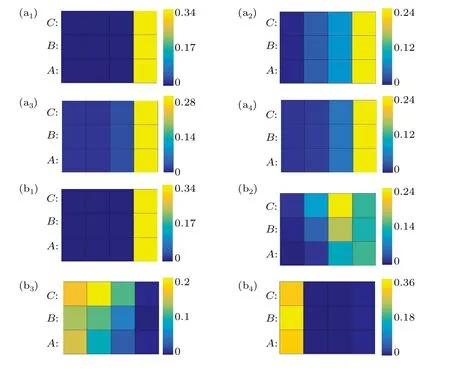
Fig.6. Densities distributions at each site with the initial state(a??A1+ a??B1+|0〉with(a1)and(b1)t=0 ns,(a2)and(b2)t=100 ns,(a3)and()t =200 ns,and(a4)and(b4)t =300 ns. ?0 =2/3π and 0.1π for(a1)–(a4)and(b1)–(b4)respectively.The common parameters are ?t=tCA=1. Here t0 is used as the unit.

5. Conclusion
In summary, we proposed a feasible experiment scheme using three legs superconducting circuits with transmon qubits to realize a hard-core Hall tube. Then we first investigate its topological properties. Since the time–reversal,particle–hole,and chiral symmetries are all broken for the hard-core Hall tube,it belongs to the A class of the Altland–Zirnbauer classification. We obtain the corresponding topological phase transition both numerically and analytically. The chirality is a key character of the quantum Hall effect,thus we secondly investigate the chiral physics in the hard-core Hall tube. In the topological nontrival phase,we find the topological protected chiral edge currents and discuss its robustness with imperfection influence. Finally,we give the possible experimental observations of the topological state and topological protected chiral edge currents in the hard-core Hall tube.




Acknowledgments
Project supported by the National Key Program of the National Health Commission’s “Thirteenth Five-Year Plan”(Grant No. NHFPC102018), the Ministry of Education Collaborative Education Program(Grant No.202101029006),the Natural Science Foundation of Shanxi Province,China(Grant No. 202103021223010), the Shanxi Province Higher Education Science and Technology Innovation Program (Grant No. J2021770), and the Natural Science Foundation of Taiyuan University,China(Grant No.21TYKQ22).
- Chinese Physics B的其它文章
- Magnetic properties of oxides and silicon single crystals
- Non-universal Fermi polaron in quasi two-dimensional quantum gases
- Purification in entanglement distribution with deep quantum neural network
- New insight into the mechanism of DNA polymerase I revealed by single-molecule FRET studies of Klenow fragment
- A 4×4 metal-semiconductor-metal rectangular deep-ultraviolet detector array of Ga2O3 photoconductor with high photo response
- Wake-up effect in Hf0.4Zr0.6O2 ferroelectric thin-film capacitors under a cycling electric field

