巖漿系統橄欖石Fe-Mg互擴散的理論基礎及其地質應用

田 野, 侯 通

巖漿系統橄欖石Fe-Mg互擴散的理論基礎及其地質應用

田 野, 侯 通*

(中國地質大學(北京), 地質過程和礦產資源國家重點實驗室, 北京 100083)

了解巖漿在演化過程中的時間尺度具有重要的巖石學意義。橄欖石作為巖漿巖中主要的造巖礦物之一, 為研究擴散年代學在巖漿系統中的應用提供了理想窗口。通過實驗測定的不同條件下的橄欖石Fe-Mg互擴散系數, 以及相關擴散模型的進一步完善, 極大地推動了礦物內元素擴散年代學的發展。本文介紹了擴散年代學的基本原理和數學模型, 并回顧和總結了以往實驗巖石學的工作, 提出溫度、壓力、氧逸度、水活度、橄欖石的成分和晶體的各向異性都會對橄欖石Fe-Mg互擴散產生影響。最后介紹了橄欖石Fe-Mg擴散模型在地質中的具體應用, 其可以約束包括巖漿上升、演化、混合等不同地質過程的時間尺度。

擴散年代學; 橄欖石; Fe-Mg互擴散系數; 實驗巖石學; 巖漿系統

0 引 言

巖漿演化過程是巖漿作用的重要組成部分。因此闡明巖漿演化過程, 如巖漿在巖漿房中滯留的時間, 是理解巖漿演化過程的重要依據。而厘清巖漿過程的時間尺度是將巖漿儲運系統(magma plumbing system)中不同空間和時間過程結合成一個整體的關鍵所在。晶體的擴散年代學不但可以用來揭示古老巖漿作用中不同階段的時間尺度, 精細刻畫巖漿演化的過程, 為理解巖漿儲運系統提供重要的理論基礎(Lynn et al., 2017; Brenna et al., 2018), 還可以與同期地震監測數據之間的緊密關聯為巖漿的上升、混合、去氣提供精確的時間框架(Albert et al., 2016), 對評估巖漿房的穩定性, 火山災害的監測和預警有重要的實際意義。

擴散年代學通過分子或元素的擴散使晶體和玻璃中的化學梯度松弛, 進而從中提取出控制不同巖漿變量下巖漿過程的時間信息(Chakraborty, 2008)。由于擴散作為記錄不同巖漿演化過程的“計時器”與巖漿事件距今的絕對年代無關, 因此作者認為相比于國內普遍將“diffusion chronometry”翻譯為“擴散年代學”, 翻譯為“擴散計時學”似乎更能說明用擴散理論限制巖漿過程相對時間尺度的核心思想, 但為了避免更多的名詞引起不必要的混淆, 本文仍用擴散年代學代指“diffusion chronometry”。礦物中擴散的普遍性使得擴散年代學在研究巖漿演化過程中的應用非常廣泛, 例如約束活火山的巖漿房穩定性(Rae et al., 2016)、估算巖漿的脫氣速率(Brenna et al., 2018)、甚至限制熔巖的流速和冷卻時間(Newcombe et al., 2014)。同時, 由于不同元素在礦物中擴散時間尺度的差異, 例如橄欖石中H和Li元素擴散很快, 而P元素擴散很慢(圖1),使得擴散年代學可以實現巖漿過程從分鐘、小時到千年尺度上橫跨多個數量級的精確定年(Costa et al., 2020)。擴散作為定年工具,約束的時間分辨率與巖漿事件距今的絕對年齡無關, 這是擴散建模最大的優勢所在(Chakraborty, 2006)。盡管原位微區同位素定年技術的發展使得傳統的同位素定年突破了不能直接獲取巖漿過程時間的限制(Rubin et al., 2017), 但仍然沒有已知的同位素衰變速度快到可以記錄小于百年尺度的巖漿活動。因此, 根據造巖礦物的擴散年代學研究巖漿演化過程的意義非凡, 甚至逐漸成為巖漿巖尤其是火山學研究的新范式(Dohmen et al., 2017)。

在火成巖眾多造巖礦物中, 橄欖石作為最常見的造巖礦物之一, 在巖漿系統尤其是中基性巖漿系統的時間尺度研究中具有不可替代的應用價值, 因而Chakraborty (2008)將對橄欖石的相關研究比喻為擴散年代學中的“果蠅”(即在遺傳學研究中起關鍵作用的果蠅)。前人已廣泛通過對基性巖漿(Costa and Dungan, 2005; Albert et al., 2015; Rae et al., 2016)或者中酸性巖漿(Coombs et al., 2000; Costa and Chakraborty, 2004; Martin et al., 2008)的橄欖石斑晶或捕虜體環帶中不同元素擴散速率的研究來限定火山噴發歷史。對于利用擴散年代學估算巖漿過程的時間尺度來說, 由于不同元素在礦物中擴散速率的差異, 選取合適元素的準確擴散系數是限制時間尺度精確性的重要因素。作為橄欖石中最主要的兩種元素, Fe-Mg互擴散研究是通過實驗巖石學獲取擴散系數最早的突破口之一(Buening and Buseck, 1973)。

本文首先介紹了礦物擴散年代學的理論基礎及數學模型, 之后利用實驗巖石學研究系統回顧和闡述影響橄欖石Fe-Mg互擴散系數的不同因素, 并綜述了相關的應用研究, 為進一步應用橄欖石Fe-Mg互擴散系數估算巖漿過程的時間尺度時提供更精準的理論模型和更精確的時間約束。

1 擴散年代學的理論基礎及數學模型

對于巖漿儲運系統中熱力學和年代學的研究許多都是基于相平衡為理論基礎, 但擴散年代學以元素在礦物與熔體間不平衡為基礎, 使其在不平衡更加普遍的自然過程中有著廣泛應用(Kohn and Penniston- Dorland, 2017)。以一個簡單的巖漿儲運系統模型為例(圖2), 在巖漿補充和混合的過程中, 與寄主高鎂玄武質巖漿平衡的橄欖石晶體被巖漿攜帶注入含有相對低鎂巖漿的巖漿房內, 此時由于巖漿混合導致原本與橄欖石晶體平衡的熔體條件發生改變, 新的熔體不再與橄欖石晶體平衡, 會在原有橄欖石基礎上生長出一個較低鎂的邊緣, 形成橄欖石環帶。熱和化學勢梯度的存在導致橄欖石內部的元素發生擴散以實現再平衡, 使原本截然的化學梯度產生松弛, 直到巖漿噴發后冷卻到擴散發生的封閉溫度之下。如果可以在適當的條件下約束出這次巖漿過程中一個較為精準的橄欖石Fe-Mg互擴散系數, 那么就可以通過模擬再平衡推算出高鎂玄武質巖漿從注入巖漿房到噴出地表的時間尺度。

圖1 常見造巖礦物不同元素的擴散時間尺度(據Costa et al., 2020)

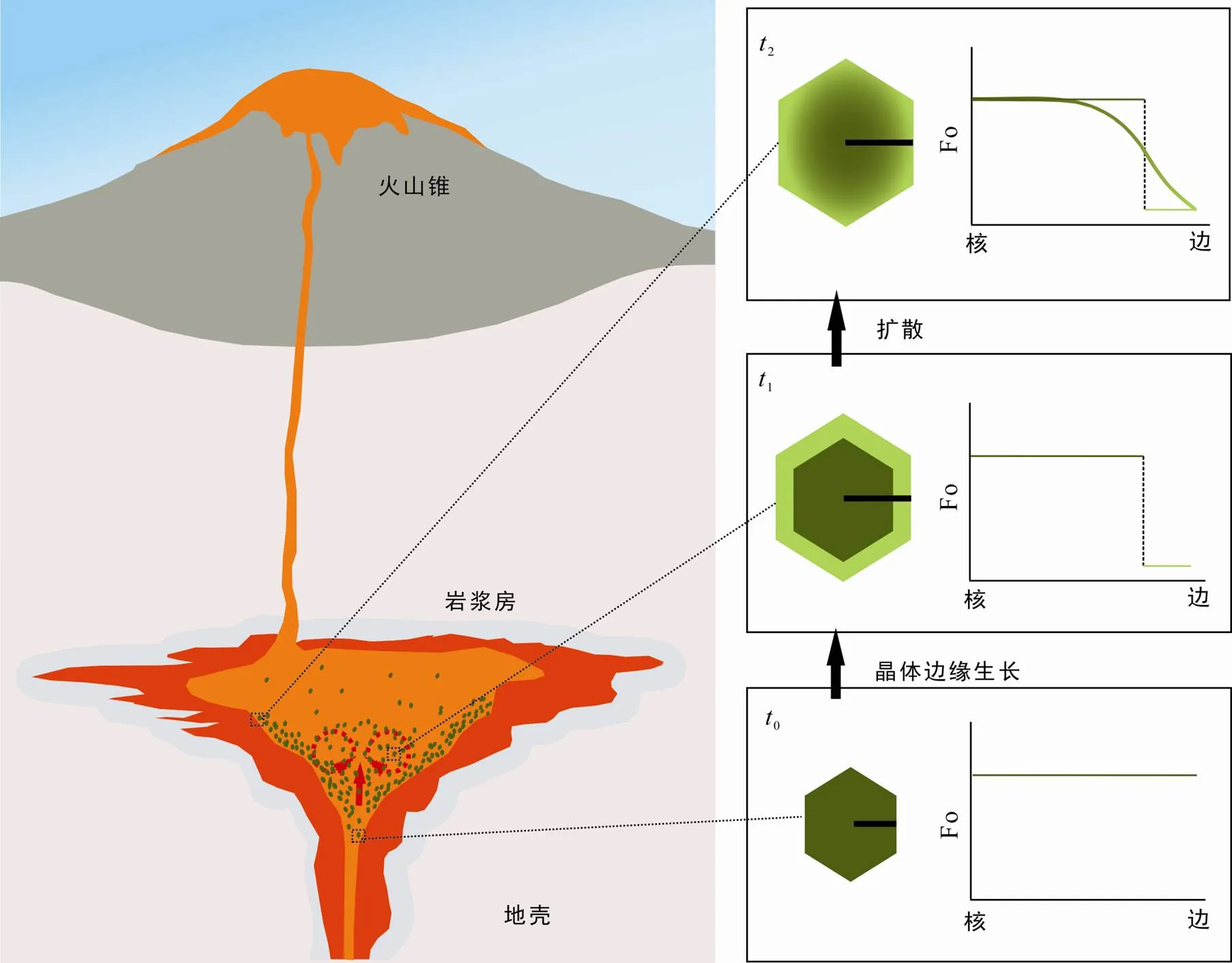
圖2 橄欖石在巖漿儲運系統中發生元素擴散的簡單模型

擴散過程中濃度與時間尺度之間的聯系是通過菲克第二定律(Fick’s second law)中二元方程的解析解來實現的。即在非穩態過程中, 在距離處, 礦物內濃度隨時間的變化率等于該處的擴散通量隨距離變化的值:

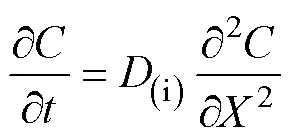
方程(1)關系到具體礦物物種(i)的擴散系數()、距離()處的濃度()和時間()之間的聯系。元素或同位素在礦物顆粒中的擴散會導致礦物內不同位置濃度的增減, 即擴散曲線上任意一點濃度的變化速率都與該點處的曲率成正比(圖3), 濃度分布的空間尺度隨著時間的推移而增大, 從而將空間和時間兩個維度緊密結合起來(Ganguly and Tirone, 1999; Ganguly, 2002)。對于常見的巖漿體系來說, 可利用玻爾茲曼變化和誤差方程(erf)求得一維無限或半無限介質中擴散的解析解:

由于擴散系數()是溫度的強函數, 因此對于伴隨從高溫中逐漸冷卻的降溫過程, Zhang (2010)提出了擴散系數隨時間變動和冷卻過程中的擴散方程:

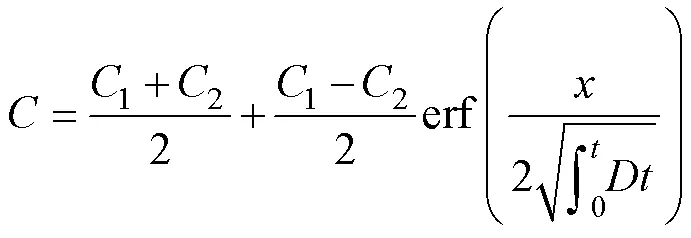
方程(3)假設擴散問題的初始條件和邊界條件相對簡單, 且擴散系數只與時間相關(擴散系數不直接與溫度相關而是通過時間與溫度綁定), 則可以對方程(2)中的做關于時間的積分。經過轉換擴散系數恒定的解析方程就可以轉換為擴散系數隨時間變化的情況, 進而應用于隨時間熔體逐漸冷卻的巖漿過程。

如果已知元素在擴散發生前熔體(1)和礦物(2)中的初始濃度以及擴散模型(包括擴散前的初始條件和邊界條件; Costa et al., 2008; Girona and Costa, 2013),則可模擬擴散剖面從而擬合時間。對于方程(1)和(2)來說, 一個準確的擴散系數()是預估時間尺度正確與否的關鍵, 擴散系數是溫度的強函數, 擴散系數與溫度的關系可用阿倫烏尼斯方程描述:

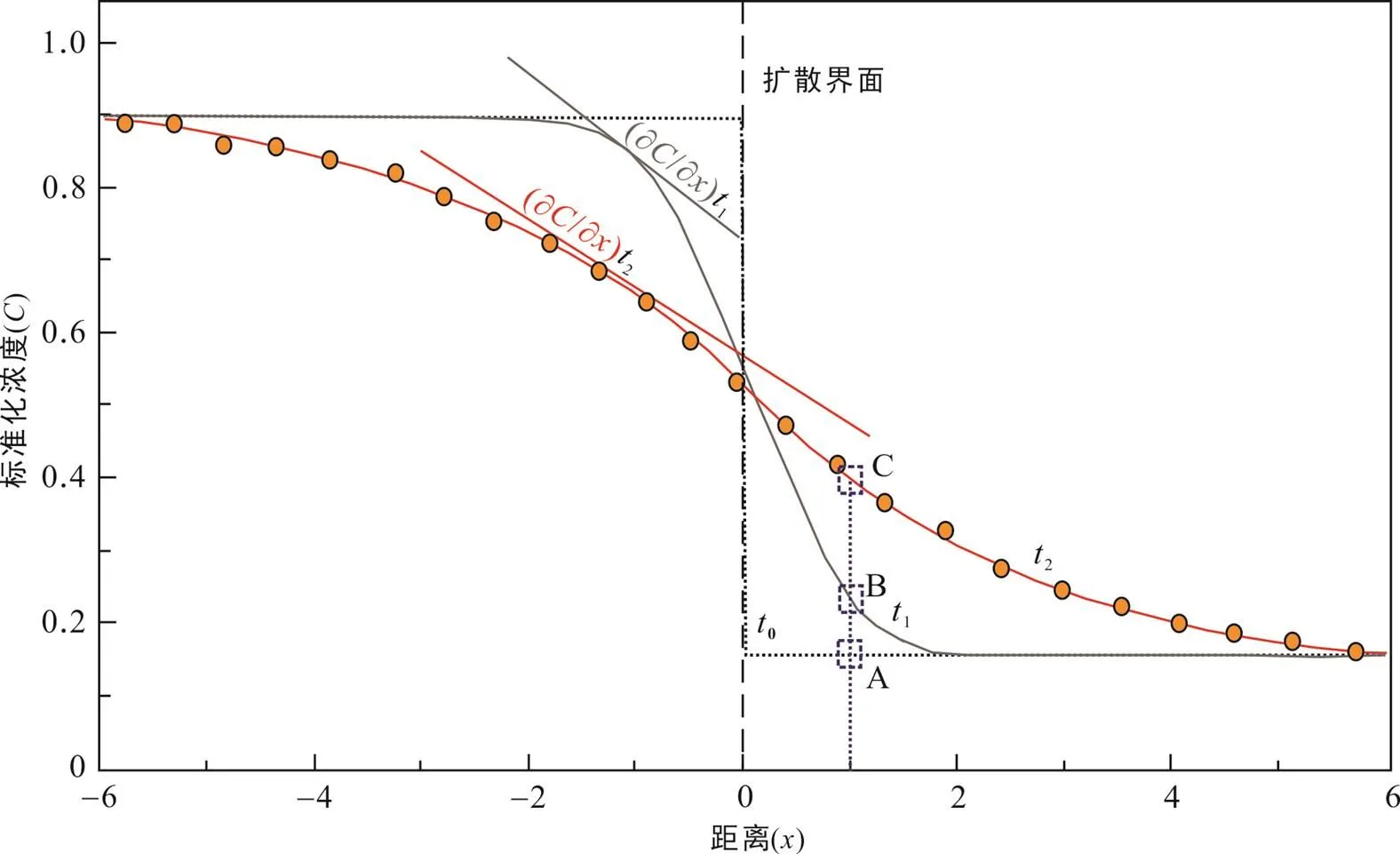
不同顏色的實線表示不同時間尺度的模擬濃度剖面。黃色圓圈表示t2時間的實測濃度, 其隨距離(藍色虛線)和時間變化。A、B、C分別代表不同時間(t0、t1、t2)在固定距離下的濃度變化。

式中:0. 前置因子(cm2/s);E. 實驗活化能(kJ/mol);. 摩爾氣體常數。擴散系數對溫度的指數性依賴意味著準確的溫度是獲得準確擴散系數的前提。此外, 實驗巖石學結果表明, 巖漿體系的氧逸度和壓力變化也可能影響擴散系數, 例如在一定溫度條件下, 體系中氧逸度增加或者壓力降低會分別增加前置因子和實驗活化能, 從而影響擴散系數(Brady and Cherniak, 2010; Chakraborty, 2010)。

除了擴散系數()以及影響擴散系數的熱力學條件外(溫度、壓力、氧逸度等), 如何給未知的天然礦物樣品匹配一個較為準確的擴散模型(初始條件和邊界條件)也是影響擴散時間尺度誤差的重要因素之一。初始條件指的是天然礦物在與其平衡的熔體中未發生擴散前相對穩定的濃度剖面形態, 其形態取決于礦物本身的性質及其相關的演化過程。Costa et al. (2008)總結了4種常見的初始剖面形態及其因擴散發生的剖面形態變化(圖4)。對于絕大多數的橄欖石擴散模型通常假設一個初始均一的剖面形態(圖4c)或階梯型的剖面形態(圖4b)(Costa and Chakraborty, 2004; Costa and Dungan, 2005; Brenna et al., 2018; Sundermeyer et al., 2020), 這兩種模型都假設橄欖石未受到晶體生長的影響, 其中圖4c表明擴散前橄欖石來自一個未發生明顯熔體成分變化(分離結晶、圍巖混染等)的巖漿儲庫或者其在驅動擴散的最終巖漿事件之前達到了平衡, 圖4b則指示橄欖石經歷了巖漿混合事件。

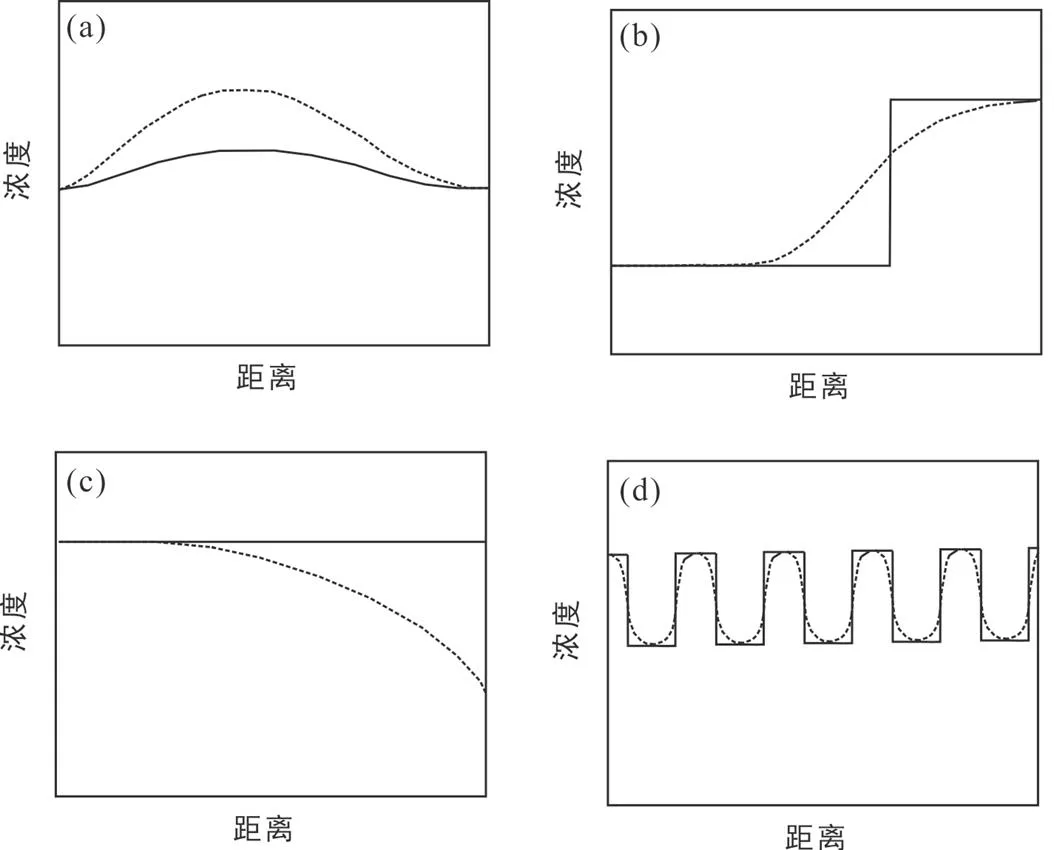
(a) 巖漿分離結晶形成的相對平滑的剖面; (b) 巖漿混合形成的階梯狀剖面; (c) 初始濃度均一的剖面; (d) 振蕩環帶形成的剖面。

在晶體生長過程中, 巖漿的分離結晶可能產生不同于圖4c的相對平滑的剖面形態(圖4a)。Costa et al. (2008)的數值模擬表明, 在控制其他變量的條件下選擇晶體過度生長的初始剖面形態(圖4a)約束的時間尺度比初始均一的剖面形態(圖4c)低約1.5倍。因此在未知初始剖面形態的情況下選擇初始均一的剖面形態或階梯型的剖面形態估算的是時間尺度的最大值(Martin et al., 2008; Hartley et al., 2016; Couperthwaite et al., 2020)。此外, 可以利用不同元素在礦物中擴散時間尺度的差異來約束過度生長對剖面形態的影響。相對于擴散發生的時間尺度來說, 一些擴散速率較慢的元素的濃度剖面仍未或者較少受到擴散的修改, 仍可以作為恢復剖面初始形態的有利依據為較快元素的擴散模擬提供初始條件的參考。例如可以利用斜長石中擴散非常緩慢的主要元素成分CaAl-NaSi (Grove et al., 1984)的剖面形狀來限制Mg元素的初始濃度剖面(Costa et al., 2003), 也可以利用透長石中擴散系數較小的Ba元素(Chernick, 2002)來約束Sr元素的初始剖面形狀(Chamberlain et al., 2014)。對于斜方輝石來說晶體生長往往優先沿軸發生, 因此對于晶型完整的斜方輝石晶體可以通過比較沿不同晶軸方向測量的時間尺度差異來檢測有無過度生長的發生(Costa et al., 2008), 但更普遍的方法仍是利用斜方輝石中擴散較慢的Al元素(Cherniak and Diamanov, 2010)的濃度剖面來為較快的Fe-Mg互擴散提供參考(Allan et al., 2013; Chamberlain et al., 2014; Cooper et al., 2017)。Shea et al. (2015)對具有骨架形態的單晶橄欖石多元素環帶(Fe-Mg、Ni、Al和P)研究表明, 從晶體學的角度來說橄欖石晶體的生長往往呈X型從拐角處沿對角生長, 而擴散則優先發生于相互垂直的晶格方向。對于橄欖石的擴散模擬來說最常用的方法是利用在橄欖石中擴散較慢的P元素(Watson et al., 2015)的初始濃度剖面形狀來作為擴散速度更快的二價陽離子(如Fe-Mg、Ni、Mn)的初始濃度剖面的參考標準(Millman Barris et al., 2008;Kahl et al., 2015; Shea et al., 2015; Albert et al., 2019)。

通常情況下, 如果晶體邊界處與熔體之間存在局部和瞬時平衡, 則可以定義邊界處的濃度(Dohmen and Chakraborty, 2003)。邊界處有無元素的擴散通量取決于該元素在礦物和熔體中的分配系數和擴散系數。當該元素在礦物中的分配系數過低、礦物的生長速度大于元素的擴散速度、甚至是熔體中的擴散速率小于礦物中的擴散速率時, 則晶體邊界處可能為僅發生物質交換而無擴散通量的封閉邊界條件。Zhang (2010)的數值模擬表明封閉邊界條件比開放邊界條件建模模擬的時間尺度要短的多。而對于絕大多數與巖漿管道系統相關的火山學研究來說, 通常假設開放的邊界條件而無物質交換, 即礦物與熔體在相對恒定的熱力學條件下局部平衡, 元素僅通過擴散相互交換, 而晶體邊緣處的濃度保持不變(圖3,在一定的擴散系數下因擴散發生的元素剖面形態的改變不會改變界面濃度)。在這種情況下可以利用礦物中擴散系數較慢元素(例如橄欖石的P和Si)的元素剖面峰值(波峰或波谷)來定義邊界條件(Brenna et al., 2018)或是利用巖漿房溫度下與熔體平衡的Fo值來定義邊界條件(Lynn et al., 2017)。

2 含鐵橄欖石Fe-Mg互擴散研究

橄欖石, 通式R2[SiO4], 具孤立硅氧四面體結構的島狀硅酸鹽礦物。其橄欖石陽離子位主要被Fe2+和Mg2+所占據, 而如何獲得準確的橄欖石與熔體之間Fe-Mg互擴散系數一直是許多巖石學家和火山學家感興趣的研究課題。實驗巖石學作為獲取擴散系數與其溫度、壓力、相和化學組成關系的唯一可靠手段, 針對橄欖石Fe-Mg互擴散的研究已經形成了一套較為完整的理論體系(Qian et al., 2010; Chakraborty, 2010)。

2.1 各向異性和橄欖石Fo值對擴散系數的影響

為了獲取由濃度差產生的擴散剖面, 初始物質的制備需要一對Fo值不同的擴散偶(diffusion couple)。出于不同的實驗目的, 不同學者對于擴散偶的制備采取了不同的方法。傳統的方法包括單晶擴散偶(Chakraborty, 1997; Petry et al., 2004; Holzapfel et al., 2007)和粉末擴散偶(Jurewicz and Watson, 1988; Spandler et al., 2007; Spandler and O’Neill, 2010)。其中前者需要制備兩塊形狀、大小相似但存在Fo值濃度差的均一橄欖石單晶, 將兩者接觸面拋光后貼合在一起進行高溫下的擴散反應; 后者則是將單晶橄欖石的拋光面和粉末接觸, 以模擬熔體或含水條件下的擴散反應。

礦物的互擴散系數實質描述的是存在化學梯度的情況下, 不同種類的兩組原子(i-j)之間的擴散行為。這兩種原子并非彼此孤立, 而是通過公式相互聯系(Lasaga, 1979):

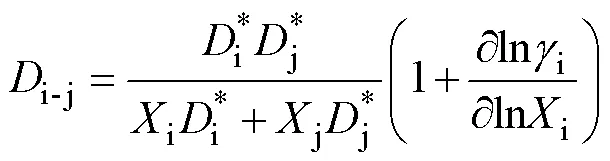
式中:i和j分別為i和j兩種組分的摩爾分數;為i組分的活度系數。從公式(5)可以看出, 橄欖石的Fe-Mg互擴散系數與其自身的Fo值(橄欖石中Fe和Mg的摩爾比例)密切相關。其他變量相同的條件下, 測量具有不同Fo值的橄欖石剖面會得到不同的擴散系數。Chakraborty (1997)在實驗中著重描述了這一點, 其在O2=10?7Pa; 980～1300 ℃的實驗條件下, 選取了兩組不同Fo差值的橄欖石擴散偶(Fa-Fo92; Fo82-Fo100)分別進行了208 小時(1000～1100 ℃)和360 小時(980～1300 ℃)的高溫退火實驗, 結果如圖6所示。

從圖6中可以直觀看出, 盡管擴散偶1相比于擴散偶2在高溫下退火了更長的時間, 但擴散偶2卻顯示出了更長的成分剖面, 表明擴散偶2具有更大的Fe-Mg互擴散系數。此外跨越Fo值范圍更大的擴散偶2在擴散界面兩側具有更明顯的成分不對稱性, 這些證據都表明隨著橄欖石Fo值的降低其Fe-Mg互擴散系數逐漸增加。早期的研究證明隨著Fa值的增加, 橄欖石固溶體的擴散系數呈指數增加約2.6～2.8個數量級(Nakamura and Schmalzried, 1984; Chakraborty, 1997)。Dohmen and Chakraborty (2007)認為在Fo30～90的范圍內, 橄欖石的成分依賴性隨Fa值增加抬升了3個對數單位(3Fe)。

O為八面體(由M位占據), T為相鄰的硅氧四面體。

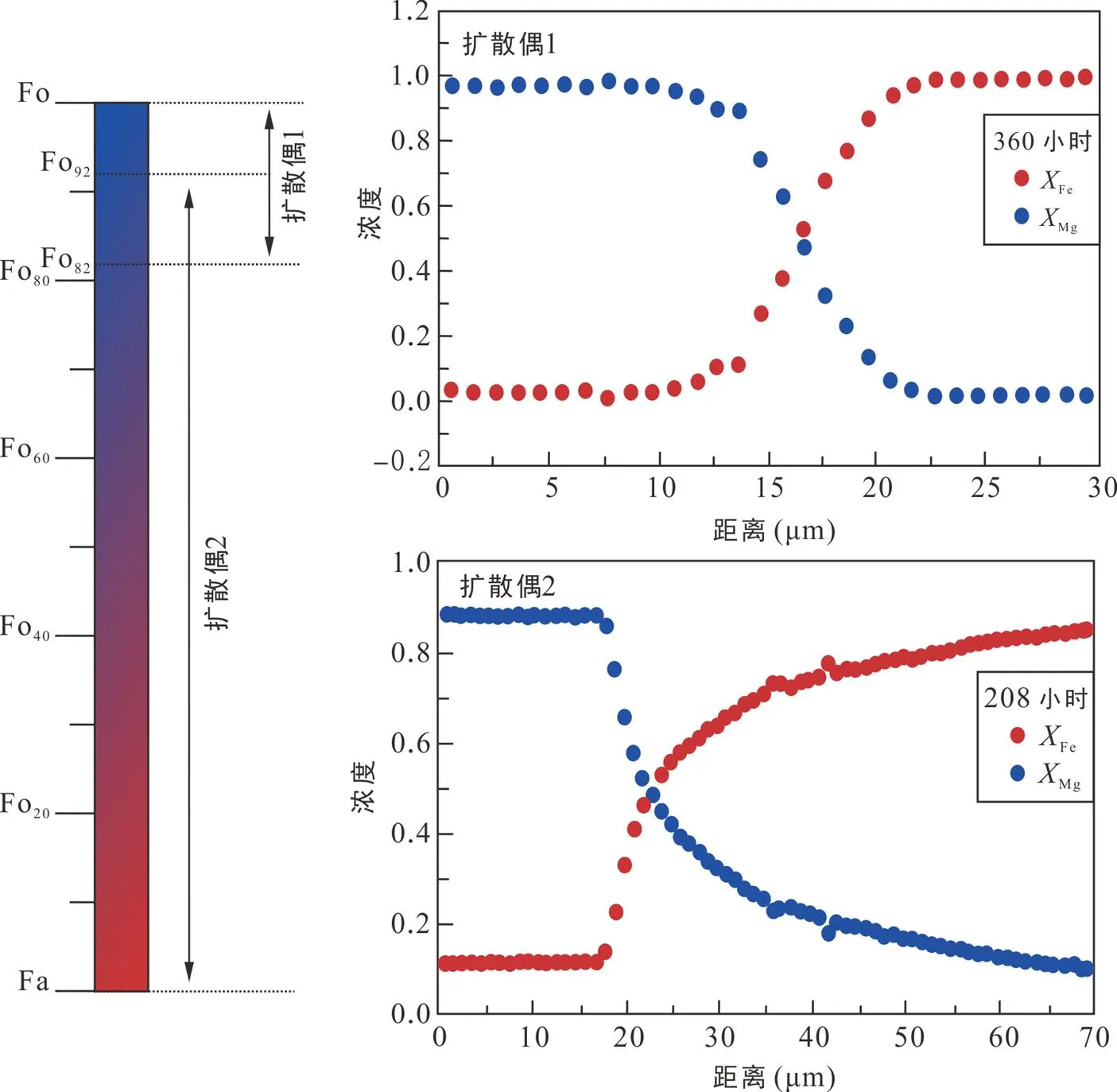
圖6 Chakraborty (1997)實驗中采用的兩組擴散偶及其測量的典型成分剖面

2.2 實驗溫度的外推——擴散機制的轉變

橄欖石Fe-Mg互擴散系數的實驗溫度早期主要集中在980～1300 ℃的范圍內(Jurewica and Watson, 1988; Chakraborty et al., 1994; Chakraborty, 1997), 這個溫度區間受到現實因素和技術因素兩個方面的制約。首先寄主玄武質巖漿的普遍溫度決定了早期實驗選取的溫度范圍是一個較為合理的區間, 然而隨著橄欖石擴散年代學向低溫領域的延伸(Jones and Rubie, 1991; Weinbruch et al., 1994), 其實驗巖石學的理論研究也需要進一步發展以支撐現實需要。其次由于擴散是溫度的強函數, 低溫實驗會導致擴散剖面過短以至于小于早期實驗設備的空間分辨率(Ganguly et al., 1988), 此外高Fa橄欖石的熔點也是限制實驗溫度向高溫拓展的一個重要因素。因此對于利用實驗巖石學測定的橄欖石Fe-Mg互擴散系數, 一個重要的問題是實驗溫度范圍內的擴散系數能否外推？

在控制其他變量的前提下, 隨著實驗溫度的改變, 如果擴散系數的對數與溫度之間的線性關系不再一致, 則其在阿倫烏尼斯公式中的斜率(即實驗活化能E)會發生變化(Costa et al., 2008; Zhang, 2010), 因此阿倫烏尼斯公式中斜率一致的區間決定了實驗溫度范圍內擴散系數的外推范圍。Buening and Buseck (1973)最早發現了這個問題, Chakraborty et al. (1994)在測量1000～1300 ℃、Fo92～100單晶橄欖石對的Mg示蹤擴散系數時, 認為隨著溫度降低橄欖石Fe-Mg互擴散系數的擴散機制由本征擴散向非本征擴散轉變。Chakraborty (1997)提出天然橄欖石固溶體存在三種不同的擴散機制(圖7a):

(1) 高溫下的本征擴散(intrinsic diffusion)。完全由點缺陷的熱力學活化能引起的擴散, 僅是溫度和壓力的函數, 與化學勢無關, 擴散發生在溫度較高和晶體雜質極少的情況下。

(2) 中間溫度下的過渡金屬非本征擴散(transition metal extrinsic diffusion)。絕大多數巖漿體系中橄欖石發生的擴散屬于此類, 由點缺陷的熱力學活化能和遷移能共同控制的擴散, 擴散與氧逸度密切相關(圖7b)。

(3) 低溫下的純非本征擴散(pure extrinsic diffusion)。完全由點缺陷的遷移能引起的擴散, 在給定的溫度和壓力下是晶體中微量元素濃度的函數。

隨著薄源法在擴散實驗中的應用(Béjina and Jaoul, 1997; Béjina et al., 1999; Dohmen et al., 2002)以及微區原位元素和同位素分析的空間分辨率提高到納米尺度(Watson and Dohmen, 2010), 對橄欖石低溫擴散過程的研究成為了可能。Dohmen and Chakraborty (2007)利用薄源法和盧瑟福背散射(RBS)分析濃度剖面確定了從過渡金屬非本征擴散向純非本征擴散的邊界條件為=900 ℃、O2=10?10Pa, 同時分別計算了兩種擴散機制下的實驗活化能為201 kJ/mol和220 kJ/mol。在高溫端元, Tachibana et al. (2013)通過實驗認為1400 ℃是本征擴散向過渡金屬非本征擴散的轉換邊界, 并得出本征擴散機制下橄欖石Fe-Mg互擴散系數的實驗活化能為280～320 kJ/mol。

固體中的擴散作用以體積擴散、晶界擴散或表面擴散三種方式進行(Freer, 1981), 而在晶體內部發生的體積擴散必須由晶體的點缺陷作為媒介(Costa et al., 2008)。晶體內空位點缺陷(晶體位置上缺少一個原子)的產生和運動必須滿足質量平衡、電荷平衡和位置平衡三個條件(Lasaga, 1980, 1981), 過渡金屬非本征擴散機制下的橄欖石擴散與氧逸度密切相關, 可利用克羅格–文克(Kr?ger-Vink)表示法進行直觀描述(Nakamura and Schmalzried, 1983):

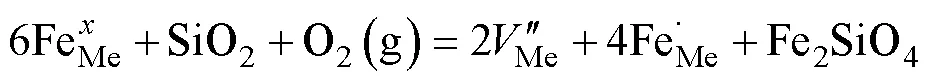
式中:表示空位缺陷; 下角標Me表示橄欖石陽離子金屬位; “′”, “”, “·”分別表示有效電荷為+1、?1和0。該公式表明金屬M位上的6個Fe2+加上 1 mol SiO2和1 mol O2可以被金屬M位上的2個空位加上金屬M位上的4個Fe3+和1 mol純鐵橄欖石取代。這個公式同時說明了與氧逸度密切相關的過渡金屬非本征擴散只在含鐵的橄欖石中有效, 而在純鎂橄欖石中不起作用(Chakraborty et al., 1994)。通過將實驗數據與作為密集變量函數的缺陷濃度相結合(Schock et al., 1989), 可以計算空位的絕對濃度在含鐵橄欖石中作為成分、溫度和氧逸度的函數(Dohmen and Chakraborty, 2007)。從圖8a中可以看出氧逸度與空位的絕對濃度呈正相關, 實驗巖石學的工作認為氧逸度在10?10～10?5Pa的范圍內含鐵橄欖石的Fe-Mg互擴散系數與氧逸度存在一個指數系數為1/4～1/6的正相關性(Petry et al., 2004; Dohmen et al., 2007), 即擴散系數隨氧逸度的增加而增大。

阿倫尼烏斯公式據Dohmen et al., 2007。

圖7 含鐵橄欖石鐵鎂互擴散機制隨溫度的變化(即阿倫尼烏斯圖解中斜率的變化)(a),以及其他控制變量條件下橄欖石下隨氧逸度Fe-Mg互擴散系數的變化趨勢(b)

Fig.7 The variation of Fe-Mg interdiffusion mechanism of iron bearing olivine with temperature (the change of slope in Arrhenius diagram) (a), and variation of Fe-Mg interdiffusion coefficient of olivine with oxygen fugacity under fixed variables (b)

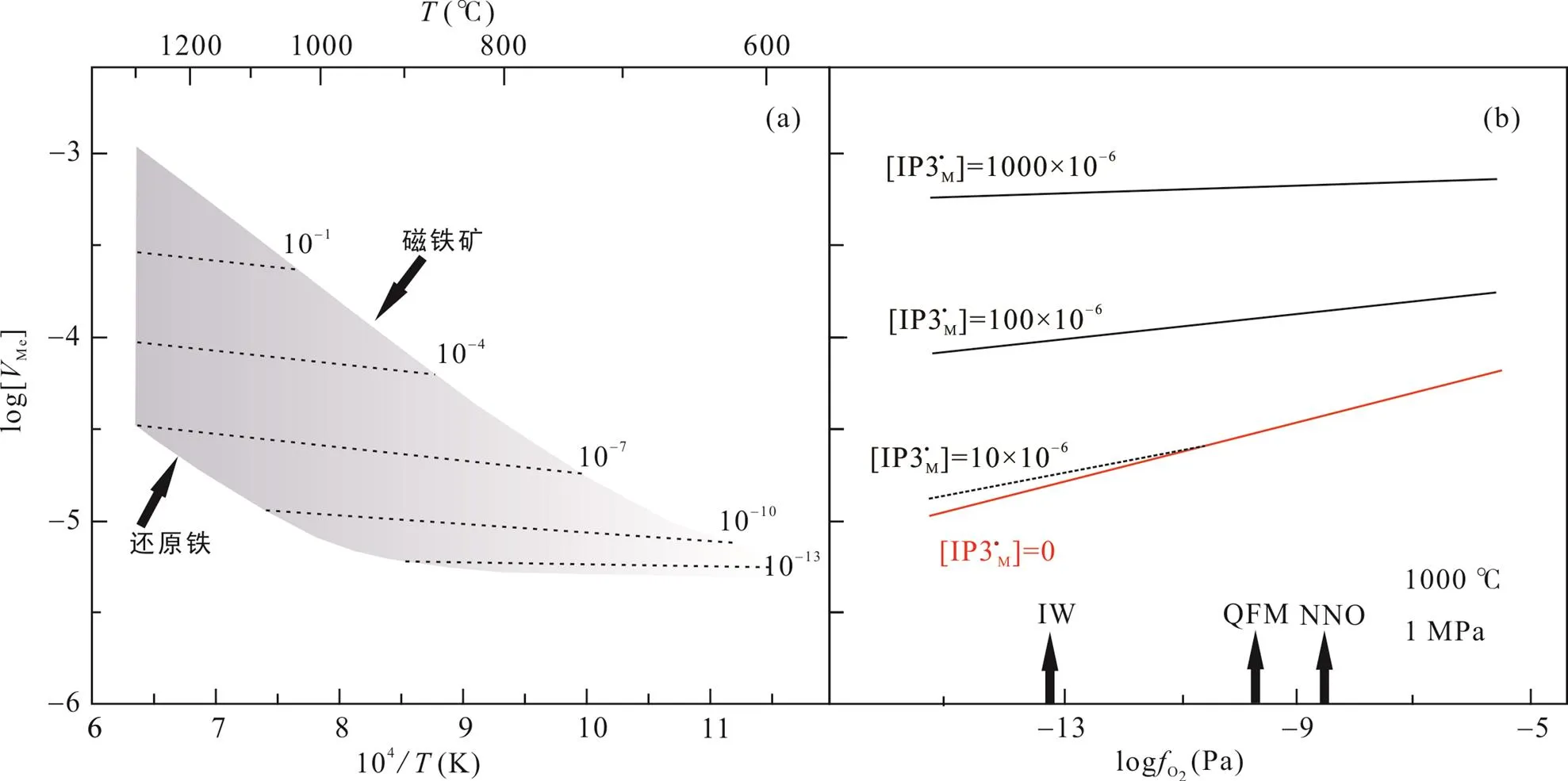
圖a中橄欖石氧化還原條件的界限分別由沉淀磁鐵礦或還原鐵界定，虛線表示恒定的氧逸度。

2.3 實驗條件的限制——壓力與水活度

相比于溫度, 壓力對擴散系數的影響要小的多, 通過對公式(4)的擴展可以探明壓力對擴散系數的影響:

式中:. 壓力(Pa); Δ. 活化體積(cm3/mol)。由于擴散系數是溫度的強函數, 高溫下壓力對擴散系數的影響往往會被溫度的強依賴性所掩蓋, 因此利用實驗巖石學對壓力的研究往往集中在低溫區間。早期的實驗利用薄源法集中研究了600～900 ℃、0.5～9 GPa下含鐵橄欖石的Fe-Mg互擴散系數(Bertran-Alvarez et al., 1992; Jaoul et al., 1995), 其中絕大多數的實驗得到了一個較小的正活化體積(Δ=0～16 cm3/mol; Farber et al., 2000; Béjina et al., 2003)。結合公式(8)表明壓力的增加反而會降低含鐵橄欖石的Fe-Mg互擴散系數。Holzapfel et al. (2007)在恒定氧逸度1673 K下測量了壓力從6 GPa到12 GPa下的含鐵橄欖石Fe-Mg互擴散系數, 得到了7 cm3/mol的活化體積, 這表明壓力從常壓增加到1 GPa時互擴散系數的變化很小(圖9), 即在地殼過程中壓力相對于溫度的變化可以忽略不計。

水活度對擴散系數的影響要結合壓力共同討論, 這是由于H在橄欖石中的溶解度會隨著壓力的增大而顯著增加(Kohlstedt et al., 1996), 在水飽和的情況下, 橄欖石中由水衍生的點缺陷空位濃度與H的溶解度呈正相關(Hier-Majumder et al., 2005)。例如在1000 ℃和300 MPa下, 橄欖石中的羥基溶解度約為1000 μg/g H/Si(Zhao et al., 2004), 而當壓力達到5 GPa時, 羥基溶解度增加到約28000 μg/g H/Si(Kohlstedt et al., 1996)。封閉含水體系下橄欖石的擴散系數實驗多通過水鎂石和滑石粉的混合物來提供過量的水(Wang et al., 2004; Jollands et al., 2016), 高溫下的脫水反應提供了摩爾比為9∶2∶11的橄欖石、斜方輝石和水, 同時將硅活度控制在斜方輝石飽和(Hier-Majumder et al., 2005)。

無水條件下擴散系數公式據Dohmen et al. (2007)和Holzapfel et al. (2007), ?O2=10～7 Pa; 含水條件下擴散系數公式據Hier-Majumder et al. (2005), ?O2=NNO。

Hier-Majumder et al. (2005)在溫度1373～1450 K、壓力0.1～6 GPa和NNO氧逸度條件下研究了飽和水橄欖石的Fe-Mg互擴散系數。實驗結果(圖9)顯示, 在低壓條件下, 相比于干體系, 飽和水橄欖石的Fe-Mg互擴散系數明顯增大; 但隨著壓力增大, 這種增大的幅度逐漸減小; 當壓力達到5 GPa時, 飽和水橄欖石的Fe-Mg互擴散系數要明顯的小于干體系。這表明當壓力影響較小時, 水會增大橄欖石的Fe-Mg互擴散系數, 而當水活度與壓力相結合時, 水會增加橄欖石Fe-Mg互擴散系數對壓力的依賴性, 即Δdry(7 cm3/mol)小于Δwet(16 cm3/mol)(Hier- Majumder et al., 2005; Holzapfel et al., 2007)。因此在地幔壓力條件下存在一條等壓線, 在此等壓線之上水會增大橄欖石的Fe-Mg互擴散系數, 而在此壓力之下干體系的橄欖石擴散速率更大。

2.4 橄欖石擴散年代學的地質應用

利用實驗巖石學對橄欖石Fe-Mg互擴散系數的詳細研究使其在實際地質環境中具有較為廣泛的應用(Morgan et al., 2004; Costa and Dungan, 2005; Albert et al., 2006; Hartly et al., 2016)。通過對其他環境變量的約束使其能較為精準的評估包括巖漿上升、補充、混合等不同作用的時間尺度。

單成因火山普遍認為缺乏明顯的巖漿演化過程(McGee et al., 2012)。然而Brenna et al. (2018)從不同元素在橄欖石中擴散速率的差異入手, 結合橄欖石Fe-Mg互擴散、微量元素擴散模型以及OH擴散模型之間不同的時間尺度對新西蘭奧克蘭火山群Pupuke單成因火山中的橄欖石捕虜體進行了時間模擬, 表明Pupuke火山在噴發前經歷了復雜的演化歷史。絕大多數橄欖石的Fe-Mg互擴散模型和其他微量元素擴散模型記錄了約30 天的擴散時間尺度(圖10a), 表明橄欖石從源區被捕獲到噴出地表的上升速率約0.01～0.03 m/s; 然而通過P等擴散速率較慢的元素模擬表明部分橄欖石顆粒顯示出過度生長的特征(圖10b), 作者將這種對勾型的擴散剖面解釋為夾帶橄欖石捕虜體的玄武質巖漿在演化過程中受到了更基性巖漿的補充(圖10c)。所有橄欖石的OH擴散模型都推導出小于1天的時間尺度(圖10d), 通過與野外高孔隙度的手標本特征相結合作者將其解釋為淺部巖漿的脫氣作用。

此外, 橄欖石Fe-Mg互擴散模型記錄的時間尺度可以與火山噴發的監測記錄相結合, 以反演淺部的巖漿補充事件。Hartley et al. (2016)在冰島東部火山帶上公元1783～1784年噴發的Laki火山三期熔巖中選取了86個橄欖石巨晶, 利用橄欖石EBSD圖像的灰度值模擬Fe-Mg擴散剖面以表征這次火山噴發前晶體儲存和運輸的時間尺度。其中少量Fo>81的橄欖石記錄了約124天的Fe-Mg擴散時間尺度(圖11b), 作者將其解釋為中地殼巖漿室中形成的晶體由于巖漿夾帶或晶粥體的動態生長上升到淺層的巖漿儲層; 而絕大多數Fo<76的橄欖石記錄了6～10 天的Fe-Mg擴散時間尺度(圖11), 短于Laki火山連續噴發之間的平均時間間隔, 表明在每個噴發期開始之前晶粥體由于寄主巖漿脈沖造成的動態分解。

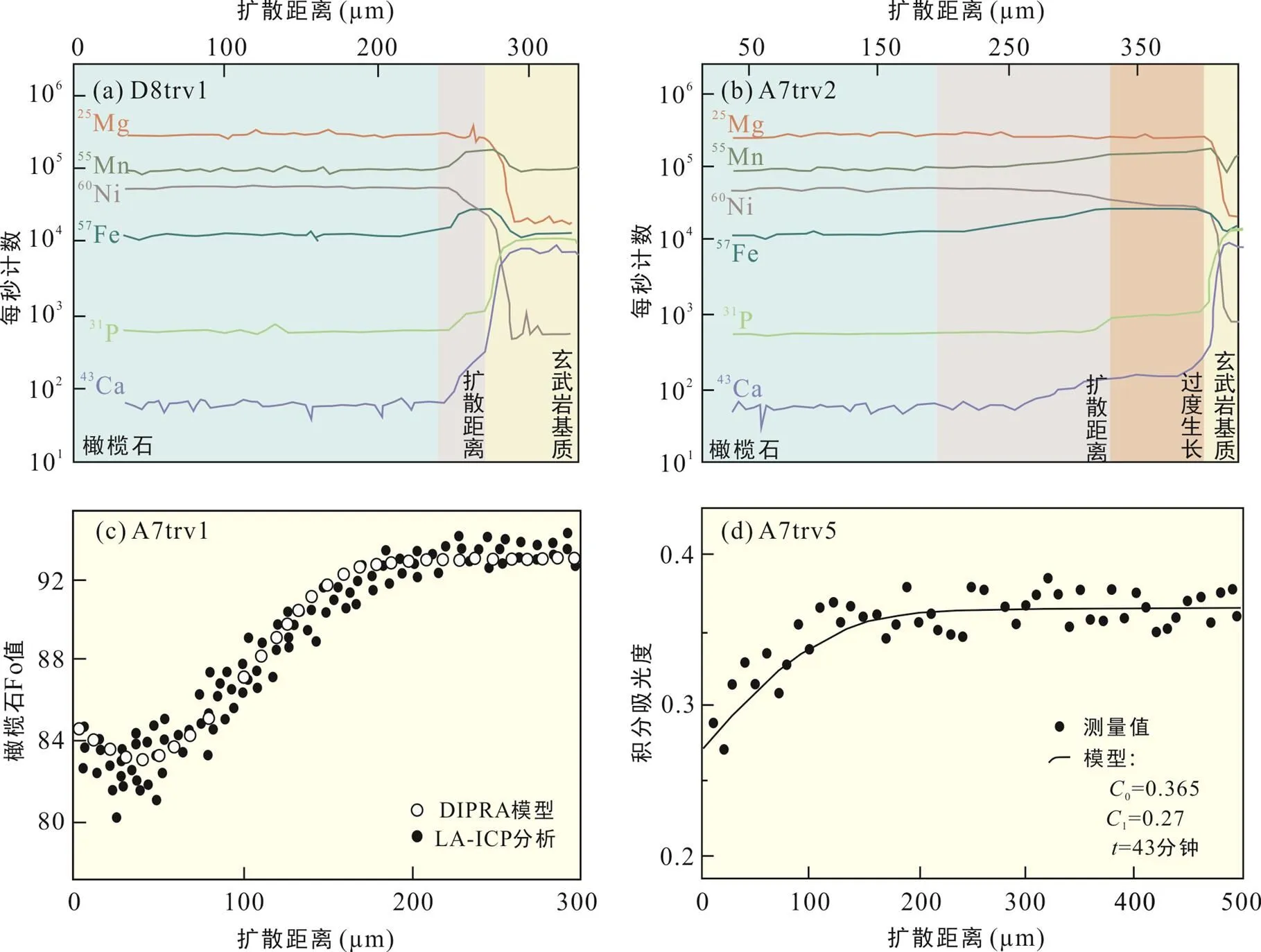
(a) 利用LA-ICP-MS技術測定的橄欖石D8trv1擴散剖面; (b) 利用LA-ICP-MS技術測定的橄欖石D8trv1擴散再生長剖面; (c) 利用LA-ICP-MS技術測定的橄欖石A7trv1擴散剖面以及擬合的DIPRA模型; (d) 利用FTIR擬合的OH擴散剖面。

(a) 按照火山單元分組(S1、S2、S3分別為依據不同火山灰單元分組的橄欖石); (b) 按照橄欖石Fo值分組。

3 結 論

擴散年代學為了解巖漿儲運系統中不同巖漿過程的時間尺度提供了精確的時間框架, 而橄欖石作為最常見的造巖礦物之一是研究擴散年代學在巖漿體系中應用的理想窗口。利用橄欖石約束時間尺度需要精確的擴散系數支撐, 實驗巖石學作為獲取擴散系數與其溫度、壓力、相和化學組成關系的唯一可靠手段, 對橄欖石Fe-Mg互擴散的研究已經形成了一套較為完整的理論體系, 為在不同地質背景下提供精確的橄欖石Fe-Mg互擴散系數作出理論指導。

橄欖石Fe-Mg互擴散系數具有強烈的擴散各向異性, 其在軸上的擴散速率比、軸快6倍左右。含鐵橄欖石具有明顯的成分依賴性, 在相同條件下隨橄欖石Fo的降低Fe-Mg互擴散系數逐漸增大。

在廣泛的溫度范圍內, 含鐵橄欖石的擴散機制會發生轉變, 這體現在實驗活化能的變化。在晶體雜質極少和>1400 ℃的高溫條件下, 橄欖石發生本征擴散, Fe-Mg互擴散系數僅是溫度和壓力的函數; 在O2=10?10～10?5Pa、=900～1400 ℃條件下, 含鐵橄欖石發生過渡金屬非本征擴散, Fe-Mg互擴散系數與氧逸度關系密切, 且隨著氧逸度增加擴散系數增大; 在O2<10?10Pa、<900 ℃的條件下, 橄欖石發生純非本征擴散, Fe-Mg互擴散系數是橄欖石中微量元素的函數。

壓力的增加會減小橄欖石的Fe-Mg互擴散系數, 但在地殼范圍內影響不大。當壓力影響較小時, 水會增大橄欖石的Fe-Mg互擴散系數, 而當水活度與壓力相結合時, 水會增加橄欖石Fe-Mg互擴散系數對壓力的依賴性。

通過對橄欖石Fe-Mg互擴散模型的深入研究, 使其可以精確約束包括巖漿上升、補充、混合等不同地質事件的時間尺度。

致謝:感謝中國科學院青年創新促進會廣州地球化學研究所小組王煜研究員的邀請, 得以將擴散計時學在巖漿儲運系統中的應用的討論撰寫成文, 供有興趣的同行共同探討。稿件評審過程中, 西北大學張超教授和中國科學院廣州地球化學研究所熊小林研究員提出了寶貴的修改意見, 在此致以誠摯的謝意。

Albert H, Costa F, Marti J. 2015. Timing of magmatic processes and unrest associated with mafic historical monogenetic eruptions in Tenerife Island., 56(10): 1945–1966.

Albert H, Costa F, Marti J. 2016. Years to weeks of seismic unrest and magmatic intrusions precede monogenetic eruptions., 44(3): 211–214.

Albert H, Costa F, Di Muroc A, Herrina J, Métrich N, Deloule E. 2019. Magma interactions, crystal mush formation, timescales, and unrest during caldera collapse and lateral eruption at ocean island basaltic volcanoes (Piton de la Fournaise, La Réunion)., 515: 187–199.

Allan A S R, Morgan D J, Wilson C J N, Millet M-A. 2013. From mush to eruption in centuries: Assembly of the super-sized Oruanui magma body., 166(1): 143–164.

Béjina F, Jaoul O. 1997. Silicon diffusion in silicate minerals., 153(3–4): 229–238.

Béjina F, Jaoul O, Liebermann R C. 1999. Activation volume of silicon diffusion in San Carlos olivine: Implications for upper mantle rheology.:, 104(B11): 25529–25542.

Béjina F, Jaoul O, Liebermann R C. 2003. Diffusion in minerals at high pressure: A review., 139(1–2): 3–20.

Bertran-Alvarez Y, Jaoul O, Liebermann R C. 1992. Fe-Mg interdiffusion in single crystal olivine at very high- pressure and controlled oxygen fugacity: Technological advances and initial data at 7 GPa., 70(1–2): 102–118.

Brady J B, Cherniak D J. 2010. Diffusion in minerals: An overview of published experimental diffusion data., 72(1): 899–920.

Brenna M, Cronin S J, Smith I E M, Tollan P M E, Scott J M, Prior D J, Bambery K, Ukstins I A. 2018. Olivine xenocryst diffusion reveals rapid monogenetic basaltic magma ascent following complex storage at Pupuke Maar, Auckland Volcanic Field, New Zealand., 499: 13–22.

Buening D K, Buseck P R. 1973. Fe-Mg lattice diffusion in olivine.:, 78(29): 6852–6862.

Chakraborty S. 1997. Rates and mechanisms of Fe-Mg interdi-ffusion in olivine at 980–1300 ℃.:, 102(B6): 12317–12331.

Chakraborty S. 2006. Diffusion modeling as a tool for constraining timescales of evolution of metamorphic rocks., 88(1–2): 7–27.

Chakraborty S. 2008. Diffusion in solid silicates: A tool to track timescales of processes comes of age., 36(1): 153–190.

Chakraborty S. 2010. Diffusion coefficients in olivine, wadsleyite and ringwoodite., 72: 603–639.

Chakraborty S, Farver J R, Yund R A, Rubie D C. 1994. Mg tracer diffusion in synthetic forsterite and San-Carlos olivine as a function of P, T andO2., 21(8): 489–500.

Chamberlain K J, Morgan D J, Wilson C J N. 2014. Timescales of mixing and mobilisation in the Bishop Tuff magma body: Perspectives from diffusion chronometry., 168(1): 1034–1058.

Cherniak D J. 2002. Ba diffusion in feldspar., 66(9): 1641–1650.

Cherniak D J, Dimanov A. 2010. Diffusion in pyroxene, micaand amphibole., 72(1): 641–690.

Coombs M L, Eichelberger J C, Rutherford M J. 2000. Magma storage and mixing conditions for the 1953– 1974 eruptions of Southwest Trident Volcano, Katmai National Park, Alaska., 140(1): 99–118.

Cooper G F, Morgan D J, Wilson C J N. 2017. Rapid assembly and rejuvenation of a large silicic magmatic system: Insights from mineral diffusive profiles in the Kidnappers and Rocky Hill deposits, New Zealand., 473: 1–13.

Costa C, Chakraborty S, Dohmen R. 2003. Diffusion coupling between trace and major elements and a model for calculation of magma residence times using plagioclase., 67(12): 2189–2200.

Costa F, Chakraborty S. 2004 Decadal time gaps between mafic intrusion and silicic eruption obtained from chemical zoning patterns in olivine., 227(3–4): 517–530.

Costa F, Dohmen R, Chakraborty S. 2008. Timescales of magmatic processes from modeling the zoning patterns of crystals., 69(1): 545–594.

Costa F, Dungan M. 2005. Short timescales of magmatic assimilation from diffusion modelling of multiple elements in olivine., 33(10): 837–840.

Costa F, Shea T, Ubide T. 2020. Diffusion chronometry and the timescales of magmatic processes., 1(4): 201–214.

Couperthwaite F K, Thordarson T, Morgan D J, Harvey J, Wilson M. 2020. Diffusion timescales of magmatic processes in the Moinui lava eruption at Mauna Loa, Hawaii, as inferred from bimodal olivine populations., 61(7): 1–20.

Dohmen R, Chakraborty S. 2003. Mechanism and kinetics of element and isotopic exchange mediated by a fluid phase., 88(8–9): 1251–1270.

Dohmen R, Chakraborty S. 2007. Fe-Mg diffusion in olivine Ⅱ: Point defect chemistry, change of diffusion mechanisms and a model for calculation of diffusion coefficients in natural olivine., 34: 597–598.

Dohmen R, Becker H W, Chakraborty S. 2007. Fe-Mg diffusion in olivine I: Experimental determination between 700 and 1200 degrees as a function of composition, crystal orientation and oxygen fugacity., 34(6): 389–407.

Dohmen R, Chakraborty S, Becker H W. 2002. Si and O diffusion in olivine and implications for characterizing plastic flow in the mantle., 29(21): 26–1–26–4.

Dohmen R, Faak K, Blundy J D. 2017. Chronometry and speedometry of magmatic processes using chemical diffusion in olivine, plagioclase and pyroxenes., 83: 535–575.

Farber D L, Williams Q, Ryerson F J. 2000. Divalent cation diffusion in Mg2SiO4spinel (ringwoodite), β phase (wadsleyite), and olivine: Implications for the electrical conductivity of the mantle.:, 105(B1): 513–529.

Freer R. 1981. Diffusion in silicate minerals and glasses: A data digest and guide to the Literature., 76(4): 440–454.

Ganguly J. 2002. Diffusion kinetics in minerals: Principles and applications to tectono-metamorphic processes., 4: 271–309.

Ganguly J, Bhattacharya R N, Chakraborty S. 1988. Convolution effect in the determination of compositional zoning by microprobe step scans., 73: 901– 909.

Ganguly J, Tirone M. 1999. Diffusion closure temperature and age of a mineral with arbitrary extent of diffusion: Theoretical formulation and applications., 170(1–2): 131–140.

Girona T, Costa F. 2013. DIPRA: A user-friendly program to model multi-element diffusion in olivine with applications to timescales of magmatic processes.,,, 14(2): 422–431.

Grove T L, Baker M B, Kinzler R J. 1984. Coupled CaAl-NaSi diffusion in plagioclase feldspar: Experimentsand applications to cooling rate speedometry., 48(10): 2113–2121.

Hartley M E, Morgan D J, Maclennan J, Edmonds M, Thordarson T. 2016. Tracking timescales of short-term precursors to large basaltic fissure eruptions through Fe-Mg diffusion in olivine., 439(5): 58–70.

Hermeling J, Schmalzried H. 1984. Tracer diffusion of the Fe-cations in olivine (FexMg1–x)2SiO4(Ⅲ)., 11: 161–166.

Hier-Majumder S, Anderson I M, Kohlstedt D L. 2005. Influence of protons on Fe-Mg interdiffusion in olivine.:, 110(2), B02202.

Holzapfel C, Chakraborty S, Rubie D C, Frost D J. 2007. Effect of pressure on Fe-Mg, Ni and Mn diffusion in (FexMg1?x)2SiO4olivine., 162(3–4): 186–198.

Jaoul O, Bertran-Alvarez Y, Liebermann R C. 1995. Fe-Mg interdiffusion in olivine up to 9 GPa at= 600～900 ℃, Experimental data and comparison with defect calculations., 89(3–4): 199–218.

Jollands M C, Burnham A D, O’Neill H C, Hermann J, Qian Q. 2016. Beryllium diffusion in olivine: A new tool to investigate timescales of magmatic processes., 450: 71–82.

Jones R H, Rubie D C. 1991. Thermal history of CO3 chondrites: Application of olivine diffusion modelling to parent body metamorphism., 106(1–4): 73–86.

Jurewicz A J G, Watson E B. 1988. Cations in olivine, Part 2: Diffusion in olivine xenocrysts, with applications to petrology and mineral physics., 99(2): 186–201.

Kahl M, Chakraborty S, Pompilio M, Costa F. 2015. Constraints on the nature and evolution of the magma plumbing system of Mt. Etna Volcano (1991–2008) from a combined thermodynamic and kinetic modelling of the compositional record of minerals., 56(10): 2025–2068.

Kohlstedt D L, Keppler H, Rubie D C. 1996. Solubility of water in the α, β and γ phases of (Mg, Fe)2SiO4., 123(4): 345–357.

Kohn M J, Penniston-Dorland S C. 2017. Diffusion: Obstaclesand opportunities in petrochronology., 83(1): 103–152.

Lasaga A C. 1979. Multicomponent exchange and diffusion in silicates., 43(4): 455–468.

Lasaga A C. 1980. Defect calculation in silicates: Olivine., 65: 1237–1248.

Lasaga A C. 1981. The atomistic basis of kinetics: Defects in minerals., 8(1): 261–316.

Lynn K J, Garcia M O, Shea T, Costa F, Swanson D A. 2017. Timescales of mixing and storage for Keanakāko‘i Tephra magmas (1500–1820 C.E.), Kīlauea Volcano, Hawai‘i., 172(9): 76–96.

Martin V M, Morgan D J, Jerram D A, Caddick M J, Prior D J, Davidson J P. 2008. Bang! Month-scale eruption triggering at Santorini volcano., 321(5893): 1178.

McGee L E, Millet M A, Smith I E M, Németh K, Lindsay J M. 2012. The inception and progression of melting in a monogenetic eruption: Motukorea Volcano, the Auckland Volcanic Field, New Zealand., 155, 360–374.

Milman-Barris M S, Beckett J R, Baker M B, Hofmann A E, Morgan Z, Crowley M R, Vielzeuf D, Stolper E. 2008. Zoning of phosphorus in igneous olivine., 155(6): 739–765.

Morgan D J, Blake S, Rogers N W, DeVivo B, Rolandi G, Macdonald R, Hawkesworth C J. 2004. Time scales of crystal residence and magma chamber volume from modelling of diffusion profiles in phenocrysts: Vesuvius 1944., 222: 933– 946.

Nakamura A, Schmalzried H. 1983. On the nonstoichiometry and point defects of olivine., 10(1): 27–37.

Nakamura A, Schmalzried H. 1984. On the Fe2+-Mg2+- interdiffusion in olivine (Ⅱ)., 88: 140–145.

Newcombe M E, Fabbrizio A, Zhang Y X, Ma C, Voyer M L, Guan Y, Eiler J M, Saal A E, Stolper E M. 2014. Chemical zonation in olivine-hosted melt inclusions., 168, 1030.

Petry C, Chakraborty S, Palme H. 2004. Experimental determination of Ni diffusion coefficients in olivine and their dependence on temperature, composition, oxygen fugacity, and crystallographic orientation., 68(20): 4179–4188.

Qian Q, O’Neill H S C, Hermann J. 2010. Comparative diffusion coefficients of major and trace elements in olivine at 950 ℃ from a xenocryst included in dioritic magma., 38(4): 331–334.

Rae A S P, Edmonds M, Maclennan J, Morgan D, Houghton B, Hartley M E, Sides I. 2016. Time scales of magma transport and mixing at Kilauea Volcano, Hawai’i., 44(6): 463–466.

Rubin A E, Cooper K M, Till C B, Kent A J R, Costa F, Bose M, Gravley D, Deering C, Cole J. 2017. Rapid cooling and cold storage in a silicic magma reservoir recorded in individual crystals., 356(6343): 1154–1156.

Schock R N, Duba A G, Shankland T J. 1989. Electrical conduction in olivine.:, 94(B5): 5829–5839.

Shea T, Lynn K J, Garcia M O. 2015. Cracking the olivine zoning code: Distinguishing between crystal growth and diffusion., 43(10): 935–938.

Spandler C, O’Neill H S C. 2010. Diffusion and partition coefficients of minor and trace elements in San Carlos olivine at 1300 ℃ with some geochemical implications., 159(6): 791–818.

Spandler C, O’Neill H S C, Kamenetsky V S. 2007. Survival times of anomalous melt inclusions from element diffusion in olivine and chromite., 447(7142): 303–306.

Sundermeyer C, G?tjen J, Weimann L, W?rner G. 2020. Timescales from magma mixing to eruption in alkaline volcanism in the Eifel volcanic fields, western Germany., 175(8): 77–100.

Tachibana S, Tamada S, Kawasaki H, Ozawa K, Nagahara H. 2013. Interdiffusion of Mg-Fe in olivine at 1400–1600 ℃ and 1 atm total pressure., 40: 511–519.

Wang Z, Hiraga T, Kohlstedt D L. 2004. Effect of H+on Fe-Mg inter diffusion in olivine, (Fe, Mg)2SiO4., 85(2): 209–211.

Watson E B, Dohmen R. 2010. Non-traditional and emerging methods for characterizing diffusion in minerals and mineral aggregates., 72(1): 61–105.

Watson E B, Cherniak D, Holycross M. 2015. Diffusion of phosphorus in olivine and molten basalt., 100(10): 2053–2065.

Weinbruch S, Armstrong J, Palme H. 1994. Constraints on the thermal history of the Allende parent body as derivedfrom olivine-spinel thermometry and Fe/Mg interdiffusion in olivine., 58(2): 1019–1030.

Zhang Y X. 2010. Diffusion in minerals and melts: Theoretical background., 72(1): 5–59.

Zhao Y H, Ginsberg S B, Kohlstedt D L. 2004. Solubility of hydrogen in olivine: Dependence on temperature and iron content., 147(2): 155–161.

Theoretical Basis and Geological Application of Fe-Mg Interdiffusion of Olivine in Magmatic System

TIAN Ye, HOU Tong*

(State Key Laboratory of Geological Processes and Mineral Resources, China University of Geoscience (Beijing), Beijing 100083, China)

It is of great petrological significance to unravel the time scale of a large range of magma residence times in different magmatic processes. Olivine as one of the major rock-forming minerals in igneous rock provides an ideal window for studying the application of diffusion chronometry in magmatic system. Improvement of Fe-Mg inter diffusion coefficient and diffusion model by advances in analytical and experimental approaches further provided new opportunities for diffusion chronometry in minerals. In this paper, we use olivine as a “reference case” to illustrate the theory and mathematical model of diffusion chronometry. On the basis of previous petrological experiments, we suggest that temperature, pressure, oxygen fugacity, water fugacity, chemical composition, and crystal anisotropy can inhibit or enhance Fe-Mg interdiffusion in olivine. We demonstrated the possible implications of olivine Fe-Mg diffusion model in natural systems and suggested that the zoning of different igneous minerals can be used to restrict the time scales of different magmatic processes from magma rising to magma transport, magma mixing and magma fractionation.

diffusion chronometry; olivine; Fe-Mg interdiffusion coefficient; experimental petrology; magmatic system

P542

A

1001-1552(2022)04-0814-015

2021-05-09;

2021-09-16;

2022-04-02

中央高校基本科研業務費(2652018120)、中國地質大學(北京)“求真學人”計劃(265QZ201901)和國家自然科學基金優秀青年科學基金項目(41922012)聯合資助。

田野(1995–), 男, 博士研究生, 礦物學、巖石學、礦床學專業。E-mail: 15620341332@163.com

侯通(1984–), 男, 教授, 從事巖漿作用及其成礦效應方向研究。E-mail: thou@cugb.edu.cn

10.16539/j.ddgzyckx.2022.02.015