問題驅動 體驗感悟 意義建構
——《分數的初步認識（一）》教學實踐與思考

文|林小平

《分數的初步認識（一）》是蘇教版三年級的教學內容，重點認識一個物體（圖形）的幾分之一。從整數到分數是數的概念的第一次擴展，又是學生認識數的概念的一次質的飛躍，將為今后學習小數及分數的意義和性質奠定基礎。

對于三年級的學生來說，要將分物的結果脫離具體的數量，以一個抽象的分數來描述分物的操作過程、結果、部分與整體的關系，理解起來并不容易。如何實現認知的突圍和生長？一是找準最近發展區，以挑戰性問題作為任務驅動整體建構生長性課堂。二是加強體驗感悟，經歷從直觀到抽象的意義建構的過程，將分數的演變史和認識幾分之一整體設計，將分數的綜合運用和數域的擴張巧妙融合，讓學生在經歷分數產生與發展的過程中理解分數。

一、問題驅動

生：后兩個是分數。

師：與以前學過的數相比，分數的長相有什么特別之處？

生：分數長得與眾不同。原來的數都是橫著寫的，分數卻是豎著寫成了兩層樓的樣子，中間還有一條橫線。

生：先寫橫線，再寫2，最后寫1。

師：在數學上，這三部分還有各自的名稱，有誰知道？

生：橫線叫分數線，2 是分母，1 是分子。

師：數學上確實是這樣規定的，橫線叫分數線，分數線下面的數叫分母，分數線上面的數叫分子。數學上還規定了，寫分數時，要先寫分數線，再寫分母，最后寫分子。

師：誰會讀這個分數？

生：二分之一。

師：對，它就讀作二分之一，是從下往上讀的。

師：我們會讀、寫分數了，也知道分數各部分的名稱了，是不是就已經認識分數了呢？你還有什么疑問？

交流后出示：

師：同學們提出了很多有價值的問題。今天這節課我們先來解決這四個問題。

【思考：借助了解學情的時機將分數的讀寫、分數各部分名稱等知識前置教學，引發學生對分數本質的溯源。通過梳理學生的問題庫，建構起“有層次、結構化、可擴展、能持續”的問題系統，以此貫穿教學的始終，引發學生深度思考，最大限度地激發學生探究、體悟和理解分數本質的熱情，開啟有意義、有意思的數學探究之旅。】

二、自主建構

1.創設情境，理解“平均分”。

師：幾千年前，古人以打獵為生。一天，有兩個人一起捕到了4只羚羊、2 只小鹿和1 只兔子，他們該怎樣公平分配呢？

生：4 只羚羊，每人2 只；2 只小鹿，每人1 只；1 只兔子，每人半只。

師：每人分得同樣多，在數學上叫作“平均分”。

生：半只是一只的一半，比0大，比1 小，不能用以前學過的整數表示。

【思考：通過創設古人分食物的情境，喚醒學生對“平均分”的原有經驗，為認識分數做好認知鋪墊。從2 只、1 只到半只，引導學生體會到當平均分的結果不能用以前學習的整數表示的時候，需要拓展數概念。從古人的符號聯想，引發對分數的猜想。】

2.直觀感知，認識二分之一。

師：像這樣兩個人分享一個物體的情況，生活中經常會遇到。春游的時候，小明和小紅在分享一個蛋糕。把一個蛋糕平均分成2份，每人分得多少？

師：對！把一個蛋糕平均分成2 份，這半個是2 份中的1 份，可以用分數來表示。那另外半個呢？

（學生操作，實物投影展示）

師：（追問）為什么要對折？

（教師示范操作，總結“折、描、涂、標”四個步驟）

學生操作后，實物投影展示并交流。

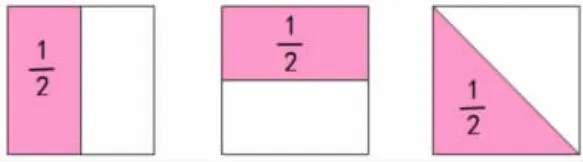
師：同樣一張正方形紙，折法不同，涂出的形狀也不同，為什么涂色部分都是它的

生：不管怎樣對折，只要是把這張紙平均分成2 份，每份都是它的

師：這個豎條也叫算籌，我國很早就用算籌來表示分數。后來印度人發明了數字，就用與我國相似的方法表示分數。再后來，阿拉伯人發明了分數線，分數就演變成了今天的樣子。這個漫長的變化過程凝聚了世界上各族人民的聰明才智。

師：請你猜猜，發明分數線是想用來表示什么？

生：平均分。

師：分母2 和分子1 各表示什么？

生：分母2 表示平均分成2份，分子1 表示這樣的1 份。

師：想一想，數學上為什么規定先寫分數線，再寫分母，最后寫分子？

生：因為寫的順序能表示出這個分數誕生的順序。

師：對了，這里的1 份是平均分的2 份當中的1 份，所以讀作二分之一，數學上稱這樣的關系是母子關系。分數的讀寫順序和分數的產生順序是一致的。

師：不管是分一個物體還是一個圖形，只要把它平均分成2份，每份都是它的

3.遷移類推，認識四分之一。

（學生操作后，實物投影展示并交流）

師：小猴歡歡和樂樂也在學習分數。它們認為下面這些圖形的涂色部分都可以用表示。它們的想法正確嗎？

（分組討論并交流）

生：因為第二個圖是將一個圓平均分成4 份，涂了其中的1份。其他圖形都沒有平均分。

師：你想提醒同學們應該注意什么？

4.抽象概括，理解幾分之一的含義。

師：下面這些圖形中也藏著分數，請你用分數表示每個圖里的涂色部分。

（學生口答并說說分數的含義）

師：其實分數在生活中隨處可見，只要你有一雙發現的眼睛，就會找到更多的分數。下面的畫面讓你聯想到了幾分之一？

師：如果讓你創造一個分數，你想創造幾分之一？在小組里說說它的含義。

師：你能用一句話來概括幾分之一的含義嗎？

生：把一個物體（圖形）平均分成幾份，這樣的一份就是它的幾分之一。

【思考：分數是一個非常抽象的數概念，要讓學生深刻理解分數的含義，一般要經歷三個層次的建模過程：第一層次是現實問題到直觀模型，第二層次是直觀模型到數學模型，第三層次是數學模型到現實問題。教學中，將分數的演變史與分數的含義、分數的讀寫緊密結合，古今溝通，加深體驗。同時，結合具體實例和操作活動，幫助學生從直觀走向抽象，經驗在經歷中積累，學力在實踐中提升。】

5.比較幾分之一的大小。

師：（出示例2）用兩張同樣大的圓形紙片折一折，涂色分別表示出它的和，并比較這兩個分數的大小。你是怎樣比的？和同桌交流。

（學生操作后，實物投影展示并交流）

師：如果將這張紙對折三次，能得到它的幾分之一？

師：你有什么發現？

生：同樣大的物體或圖形，平均分的份數越多，每一份就越小。

【思考：緊密聯系幾分之一的含義教學分數的大小比較，既是出發點，也是落腳點，兩者相輔相成。這里有直觀、推理、想象等多種思維方式的加持，便于學生觀察、比較、發現、歸納、總結，在應用中豐富了對幾分之一的認識。】

三、綜合應用

師：剛才我們認識了幾分之一，并能比較它們的大小了。擁有了這些本領，就可以到分數王國去闖一闖啦！有信心接受挑戰嗎？

1．“想想做做”第3 題（圖略）。

師：下面進入第一關“考考你的眼力”。《科學天地》大約占黑板報的幾分之一？《藝術園地》呢？

師：如果想在第3 版面加入《名人名言》和《每周一星》兩部分內容，你打算怎樣設計？《名人名言》和《每周一星》大約各占黑板報的幾分之一？在小組里說說你的想法。

（學生小組討論后匯報交流）

2．“想想做做”第5 題。

師：下面進入第二關“會變的長方形”。這是一個長方形，給它全部涂上顏色，可以用哪個數來表示？下面變身開始啦！

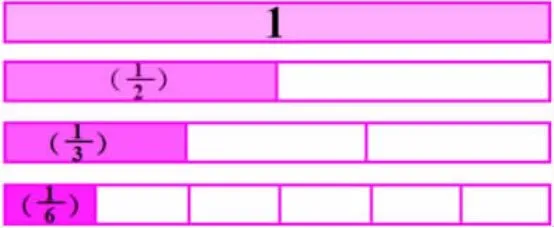
師：如果繼續平均分下去，每一份會變得怎樣？

生：每一份越來越小，表示的分數也會越來越小。

課件演示將這些長方形重疊，幻化出一條數線。

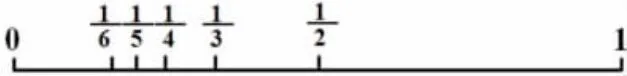
師：如果最左端表示0，最右端表示1，這些分數就密密麻麻地排列在0 到1 之間的數線上。你能說一個比還小的分數嗎？

（學生舉例，發現這樣的分數有無數個）

3.變式拓展題。

師：同學們的表現太出色了，歡歡和樂樂想出道題考考大家，愿意接受挑戰嗎？課件出示：

（學生小組討論后交流）

師：分數真是太神奇了！今后我們還會繼續研究這種神奇的數。

【思考：對書本練習進行深度改造和加工，將分數的含義、數域擴張、數的無窮性、數的大小等知識整合設計。既凸顯知識的本質特性和應用價值，又培養學生的創造精神和實踐能力，擴展并完善學生的認知體系，體現知識的生長性，提高教材的附加值。】

四、全課總結

師：今天我們初步認識了幾分之一，回頭看看，課始的四個問題都解決了嗎？談談你們的收獲。