水下航行器-發射筒間隙流動仿真

劉元清,張晨星,陳香言,王凡瑜

(北京宇航系統工程研究所,北京,100071)

0 引言

固定在筒壁的減振墊-氣密環方案具有結構簡單、可重復使用、無伴隨航行器運動分離物導致的碰撞安全隱患等優點,是水下航行器與發射筒間隙適配方案的發展趨勢[1-3]。為了對水下航行器進行橫向支撐約束并提高支撐強度、保持筒內壓力以保證出筒速度,往往需設置多道氣密環結構,從而將間隙沿航行器長度方向分割成多個完全密閉或半密閉獨立腔室。當航行器尾部經過氣密環時,筒底高壓高溫氣體將進入航行器-發射筒-氣密環組成的間隙腔,劇烈的壓差使其內部瞬間充壓,呈現出高速和分離流動等復雜特征,其將承受較大沖擊載荷;而多個間隙腔室的連通過程則使得航行器出筒過程經歷多次劇烈壓力振蕩。因此,航行器-發射筒間隙流動對氣密環、發射筒及航行器載荷特性具有重要影響,已成為發射系統設計的重要內容之一[4-6]。

尚書聰等[2]建立了采用氣密環結構的導彈出筒過程橫向動力學模型,表明劇烈的載荷振蕩導致航行器運動不平穩。秦麗萍等[7]采用數值仿真研究了氣密環透氣孔結構的流量規律與各間隙腔壓力演化特性,并進行了試驗驗證,當航行器尾部通過氣密環時,小孔質量存在突變增加和突變減小現象,而腔內壓力則出現強烈振蕩現象。陳前昆[8]對氣密環變形測試技術進行了研究,得到了發射筒不同位置變形特性,為發射過程航行器與氣密環相互作用研究提供了參考。趙世平[9]和劉傳龍[10]等的研究表明,水下垂直發射時適配器剛度對航行器出筒過程受力特性具有重要影響。朱珠等[11]建立了潛空導彈垂直出筒動力學模型,導彈和適配器受力均出現了復雜振蕩現象,并隨著發射平臺航速增加而劇烈惡化。

綜上可知,水下航行器發射過程適配的載荷特性極為復雜,尤其是在發射之前,筒內充氣壓力與水深環境相同,發射筒及航行器均承受較大初始載荷;在出筒過程中發射平臺運動導致的橫流沖擊加劇以上結構載荷。此外,由于彈射過程筒底壓力遠高于筒內初始壓力,當航行器尾部經過氣密環時導致復雜的壓力振蕩[7],進一步惡化航行器-發射筒結構的載荷特性,但目前對此問題的詳細研究較少。因此,文中將針對航行器尾部與兩道氣密環間的間隙腔連通過程開展動態非定常仿真研究,詳細探討間隙內流場演化、壓力脈動幅值與頻率等特征,并對比3 種連通初始壓比和3 種航行器運動速度對間隙流動的影響,分析其作用機制,為航行器-發射筒結構設計、氣密環設計與降載優化等提供參考。

1 研究對象與數值方法

1.1 研究對象

圖1(a)給出了水下航行器與發射筒適配模型示意圖。航行器垂直發射,發射筒內有多道固定在筒壁上的氣密環,發射過程中,通過筒底高溫高壓氣體將航行器彈出(運動方向指向水面),在出筒過程中航行器尾部將依次經過各道氣密環而使得發射筒底部高壓氣體與間隙腔連通,在此過程中將產生復雜的壓力脈動和非定常流場演化。針對某航行器兩道氣密環間的間隙腔進行研究。由于航行器及發射筒均為軸對稱結構,出筒過程仿真中常采用二維軸對稱模型[12-14]。圖1(b)給出了發射初始狀態時的軸對稱計算域,所考慮的流體區域包括發射筒底部區域及氣密環與航行器和發射筒壁面組成的間隙腔,該間隙腔長度與寬度的比值為340∶1,間隙寬度為50 mm。在航行器尾部布置了8 個監測點(分別用m1～m8 標記),以研究發射筒底部與間隙腔連通時的壓力振蕩特性,監測點m1～m8 距航行器尾部的距離分別為0,100,200,300,400,800,1 200 和1 600 mm。

圖1 水下航行器與發射筒模型Fig.1 Models of undersea vehicle and launch tube

針對發射筒底部與間隙腔3 種不同初始壓比(pt/p0=2.0,2.5和3.0,其中pt為發射筒底部彈射氣體壓力;p0為間隙內初始壓力,即當地水深壓力)和航行器3 種不同運動速度(V=10,15,20 m/s)探討動態運動連通過程中間隙內流動演化和壓力脈動規律及機制。由于航行器運動速度遠小于間隙腔連通時的氣體速度,且航行器質量較大,在其尾部經過氣密環1 和氣密環2 時的速度差別較小,因此可假定該過程中航行器勻速運動。

1.2 數值方法

采用Ansys fluent 軟件進行仿真計算,采用可壓縮氣體,給定發射筒底部的彈射氣體壓力,其溫度為500 K,湍流模型為標準k-ε模型。采用動網格技術模擬航行器運動,由于筒內航行器一自由度運動,通過層變方式更新運動過程中的計算網格。

由于間隙寬度小、氣密腔狹長,在尾部與氣密腔連通時內部流動較為復雜,計算網格疏密對間隙腔內壓力脈動、速度變化等的精確捕捉具有重要影響。因此,首先開展了計算網格對仿真結果的影響研究,如圖2 所示,網格總數分別為30 000、60 000 及120 000。從圖3 中監測點m8 (所設置的監測點中該點壓力脈動幅值最大) 處壓力來看,3 種網格條件下壓力極大值、極小值及壓力脈動周期基本相同。此外,秦麗萍等[7]的仿真及實驗也觀測到以上相同的壓力振蕩現象,從而驗證了結果的合理性。而從圖4 中連通后某時刻間隙馬赫數來看(為了清晰顯示間隙內流動演化,視圖中對間隙寬度進行了7 倍放大處理,后文流場結構及云圖均按此方法進行處理),高速區分布范圍差別較小;當網格數為60 000 和120 000 時,其最高馬赫數基本相同,而網格數為30 000 時略低。因此,以上3 套網格均較密,加密網格對壓力脈動計算結果影響較小,在后續研究中,所采用計算網格的總數為60 000。

圖2 間隙計算網格對比Fig.2 Comparison of grids in the gap

圖3 不同網格數下監測點m8 處壓力對比Fig.3 Comparison of pressure at monitoring point m8 under different grid numbers

圖4 連通后某時刻馬赫數對比Fig.4 Comparison of Mach numbers after connection

2 結果與分析

2.1 間隙流動與壓力脈動特性分析

針對發射筒底部與間隙腔內初始壓比為pt/p0=2.5、航行器速度V=15 m/s 工況下,詳細分析間隙流場演化特性。從圖5 中監測點壓力可以看出,隨著航行器的運動,當其尾段壁面監測點進入間隙腔且發射筒底部未與該間隙腔連通時,其壓力降低;當發射筒底部彈射氣體與間隙腔連通后,筒底高壓氣體進入使得其內部壓力急劇升高,并出現較大的壓力峰值;隨著航行器的進一步運動,各監測點壓力呈類似正弦波動下降趨勢,但其脈動周期基本不變,約為13 ms。監測點離航行器尾部越遠或者說連通時離氣密環2 越近,其壓力波動越大,壓力峰值越大。從圖5(b)中連通后初期的壓力進一步可看出,航行器壁面壓力脈動的最大峰值可達1.0p0,脈動壓力谷值約為0.5p0。

圖5 監測點壓力變化Fig.5 Pressure changes at the monitoring points

圖6 和圖7 給出了從間隙連通后(連通時刻為t0)至第1 個壓力谷值時間段內6 個不同時刻的流線、馬赫數和壓力分布。馬赫數分布表明,當間隙腔與航行器尾部連通時,由于發射筒底部壓力遠高于間隙腔內初始壓力,形成了高速縫隙泄漏流動,局部馬赫數大于1。從流線可以看出,彈射氣體進入間隙腔后首先撞擊發射筒壁面,而后沿狹小間隙向氣密環2 流動,直至沖擊其壁面并反射,在間隙內形成復雜的旋渦流動,進而向筒底反流,但此時其流速較低。結合圖7 中的壓力云圖可知,此時筒內壓力將急劇升高,即間隙內的壓力峰值由筒底向間隙內泄壓的高速氣流沖擊另一道氣密環受阻所致,因此,氣密環2 將受到較大沖擊載荷。此后,在較長時間段內氣流始終向筒底反流,直至間隙內壓力再次下降并達到極小值后 (對應前文圖5 中的第1 個壓力谷值),筒底氣流將再次進入間隙內,直至從氣密環2 壁面反射使得間隙內壓力再次升高。但由于此時隨著航行器的運動,筒底與間隙腔的連通區域增大,間隙內初始壓力更高,氣流沖擊氣密環2 的壓力峰值也隨之減小。結合前文圖5(a)可知,直至航行器尾部運動至氣密環2 時,該間隙內將反復出現多次壓力脈動或者說高速泄漏流動沖擊,流動分離呈現出劇烈的非定常演化特征。

圖6 連通后間隙內不同時刻的馬赫數和流線Fig.6 Mach numbers and streamlines in the gap after connection

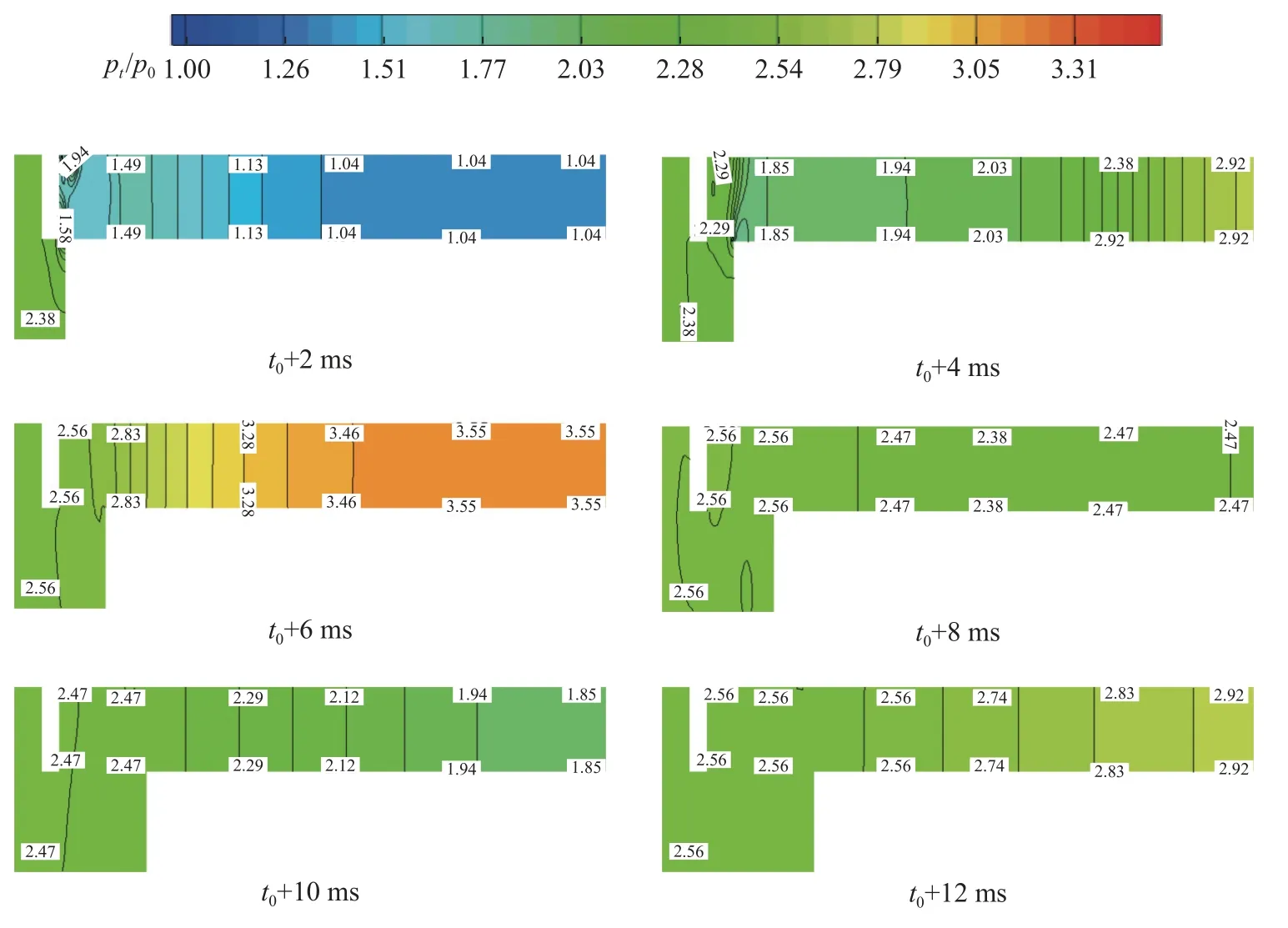
圖7 連通后不同時刻的壓力分布云圖Fig.7 Contours of pressure in the gap after connection

2.2 初始壓差對流動與脈動的影響

圖8 給出了不同初始壓差下最大壓力的監測點8 壓力對比。可以看出,不同初始壓比pt/p0下的壓力脈動規律相同,連通后較短時間內出現了明顯的沖擊壓力峰值,而后監測點壓力急劇減小,直至達到極小值后再次增加。不同初始壓比下沖擊峰值出現的時間及周期基本相同。初始壓比越大,壓力脈動愈加明顯,如圖9 中給出的沖擊壓力峰值和谷值相對初始壓比的變化所示,脈動壓力的相對極大值和極小值均隨著初始壓比的增加而線性變化。

圖8 監測點m8 處壓力對比Fig.8 Comparison of pressure at monitoring point m8

圖9 脈動壓力峰值隨初始壓比變化曲線Fig.9 The peak value of pulsating pressure with different initial pressure ratio

圖10 給出了不同初始壓比下第1 個沖擊壓力峰值時刻間隙內壓力分布云圖對比。可以看出,間隙內壓力分布趨勢相同,靠近氣密環2 區域壓力高,而氣密環1 附近壓力低,從而形成了明顯的壓力梯度,因此氣流必然將由氣密環2 向發射筒底部回流。圖中還表明,初始壓比越大,相同位置處筒內壓力也越高,即壓力脈動也愈加明顯。

圖10 第1 個沖擊峰值時刻間隙內壓力分布Fig.10 Pressure distribution in the gap at the moment of the first impacting peak

2.3 航行器運動速度的影響

進一步研究不同航行器運動速度下間隙腔內的流動與壓力脈動特性,3 種速度分別為V=10,15,20 m/s。圖11 中給出了監測點8 在間隙連通后的壓力變化,其中橫坐標為相對連通時刻的時間變化。可以看出,3 種工況下間隙內壓力脈動趨勢相同。但從其數值來看,隨著航行器運動速度的增加,由于連通區增長加速,發射筒底部高壓氣體向間隙腔內的泄漏流量增大,從而使得監測點壓力升高速度加快,且第1 個沖擊壓力峰值更大,而氣流反射后向發射筒底部反流時的壓力谷值也更小,即壓力脈動幅值增加。從時間演化來看,3 種速度下壓力脈動周期相同,約為13 ms,即脈動周期不隨航行器運動速度變化。

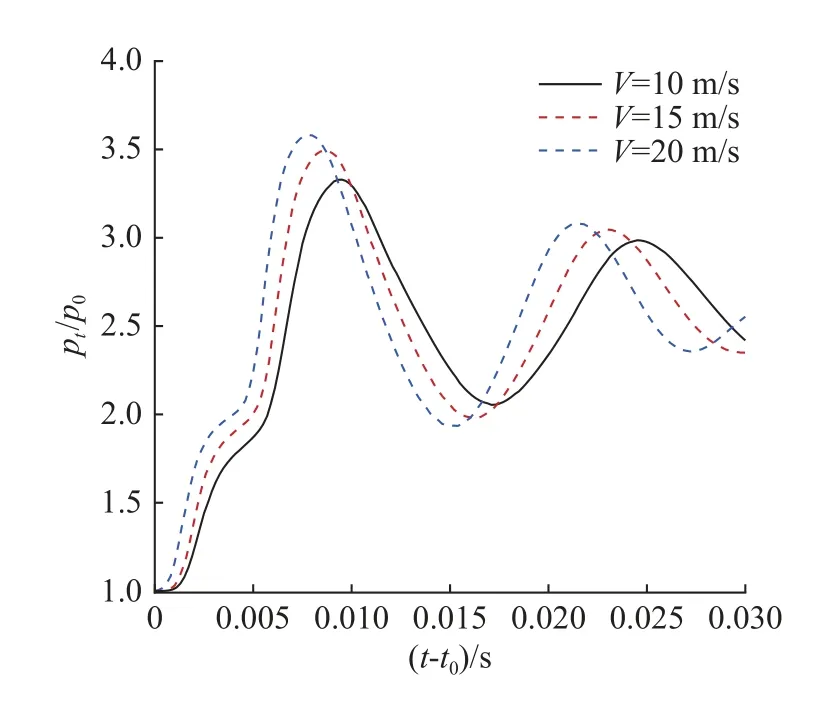
圖11 連通初期監測點m8 處壓力對比Fig.11 Comparison of pressure at monitoring point 8 in the initial stage of connection

圖12 中給出了連通后在第1 個沖擊壓力峰值出現前航行器尾部距氣密環1 在某一距離相同條件下的間隙內動壓分布對比。可以看出,當航行器運動速度較快時,泄漏量增加,間隙高動壓區范圍越大,此時間隙內流速度更高,由筒底氣體發展后沖擊氣密環2 時滯止壓力也更大,即間隙內壓力脈動峰值提前且數值更大。

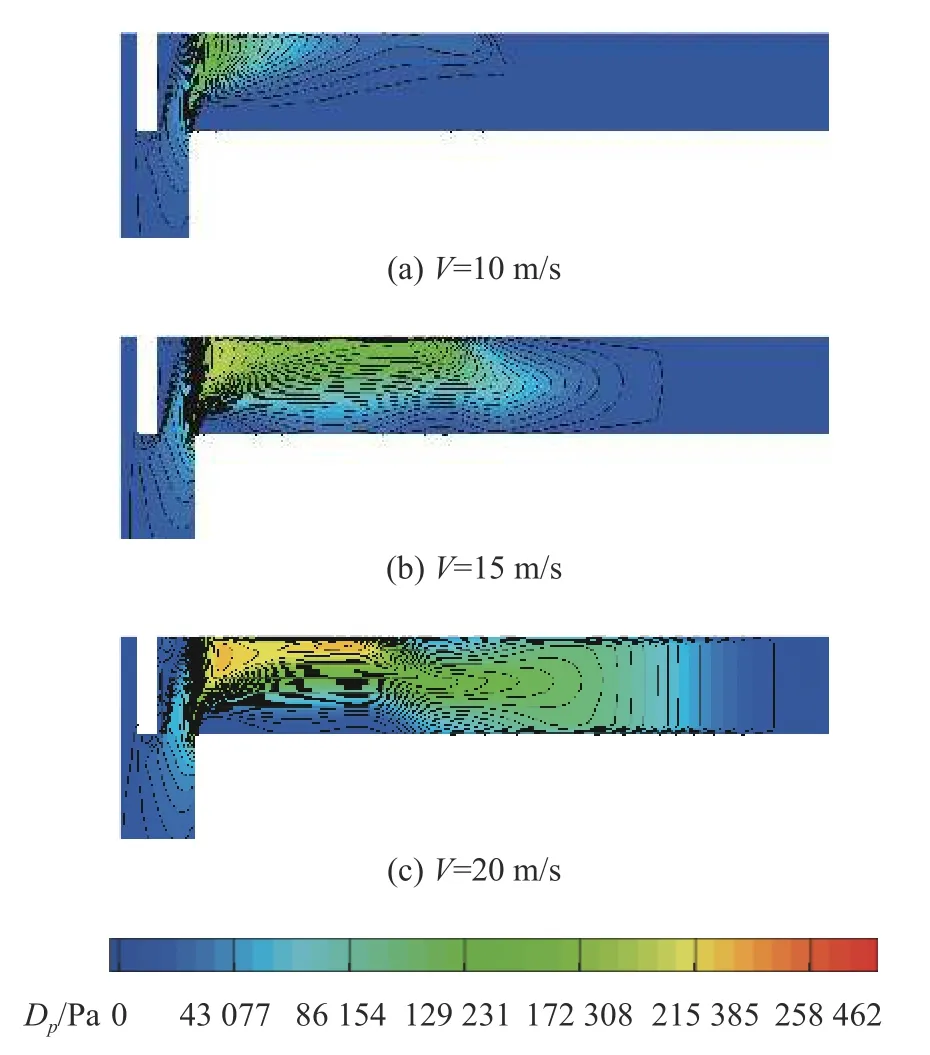
圖12 相同連通距離下間隙內動壓對比Fig.12 Comparison of dynamic pressure in the gap under the same connecting distance

3 結論

通過不同連通初始壓比和航行器運動速度下間隙流動的動態非定常數值仿真表明:

1) 航行器尾部經過氣密環時,發射筒底部高溫高壓氣體進入間隙腔后將產生局部超音流動,氣流在沖擊遠離筒底的氣密環后反射并產生復雜的非定常分離流動,壁面承受劇烈的高頻脈動壓力載荷;

2) 隨著初始壓比pt/p0增加,沖擊壓力幅值相對變化量線性增加,在pt/p0=3.0 時,航行器壁面壓力脈動的最大峰值可達1 倍初始間隙壓力,最大谷值約為0.5 倍初始間隙壓力;

3) 當發射筒底部與間隙腔連通時,航行器運動速度越大,泄漏量越大,壓力脈動幅值增大且峰值提前,脈動頻率不隨初始壓比與航行器運動速度變化。

基于以上研究,可以進一步開展間隙寬度、長度及開孔結構等對非定常流動及壓力脈動的影響,并探討發射筒、航行器及氣密環的降載設計方法。