基于彈性理論設計邊坡防護方法研究

徐 立，劉 晗，呂俊秀，干 鋼

（浙江大學建筑設計研究院有限公司，浙江 杭州 310000）

巖土體都處于天然應力場[1-2]中，天然應力場包括垂直應力和水平應力2部分，垂直應力主要是自重應力，可根據經典土力學理論計算；而水平應力影響因素較多，一般難以準確計算，大多通過試驗進行量測。此外，土體是三相體，受力后變形不同于理想彈性材料，但縱觀整個土力學發展歷程及近年來大量工程實踐經驗，將彈性理論運用于土力學計算，并指導設計，誤差滿足工程要求。為便于計算，在討論相關問題時，不考慮天然土體中水平應力，并將土體簡化為理想彈性材料。在巖土體中開挖邊坡，原土體狀態將會改變，且應力場將重新分布，稱作為卸荷作態[3]。卸荷狀態會在邊坡中形成卸荷影響帶，這個影響帶有一定范圍，超過這一范圍后，土體的應力狀態可認為和原來狀態相同。如果能知道原狀態中各個方向應力分布情況，然后在設計邊坡開挖線上施加一個作用力，這個作用力對邊坡線產生的效應與邊坡將要挖除的那一部分土體對邊坡線施加的作用效應相一致，那么，對于理想彈性材料[4-8]而言，這個狀態是等效的。

應該指出，土是三相體，不同于理想彈性材料，他具有特殊性，如土體卸荷再壓縮時，表現出的性質與原狀土壓縮時的性質有所不同，因此直接將原狀土內的應力狀態用開挖后的邊坡加某一外荷載來等效，理論上不嚴密。但由此引出的開挖影響范圍概念是正確的，若考慮一定安全系數，采用這種方法進行設計可行。以西南山區某高填方邊坡為例，在對地質概況進行了詳細調查的基礎上，對邊坡在不同工況下的穩定性進行計算評價研究。

1 開挖影響區概念和計算

1.1 開挖影響區概念

邊坡開挖后坡體內部應力和變形變化情況如圖1、圖2所示。由圖2可知，距坡面距離增大，邊坡坡體內部應力及變形均逐漸趨于穩定。應力趨于原始坡體的應力，而變形則逐步縮小，直至可以忽略。這表明，由于邊坡開挖，坡體內部的應力及變形在某一范圍內影響較大，這一影響范圍稱為開挖影響區。工程經驗表明，坡體失穩是由于坡體內部發生了較大的位移和變形造成的。邊坡開挖影響區內，坡體應力重分布和變形顯著，是失穩破壞的主要區域。

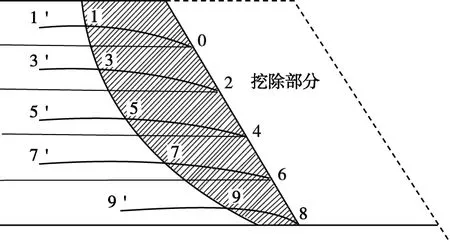
圖1 應力作用范圍Fig.1 Stress range

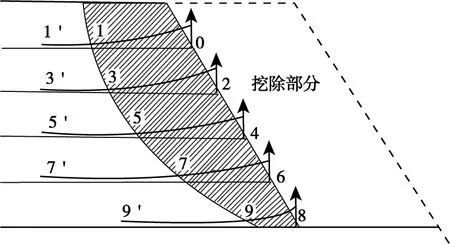
圖2 應力形變范圍Fig.2 Stress deformation range

1.2 開挖影響區計算

理論上，邊坡開挖影響區應通過彈性力學方法，分析邊坡坡體內部各點位移情況，作出位移曲線圖，由曲線圖進行計算。但這樣分析計算稍顯復雜，有的學者通過敏感性分析，提出相應計算公式，并完成了相應的工程驗證。設開挖影響區寬度為B，開挖高度為H，開挖角度為β，開挖臺階寬度為b，邊坡巖土體內摩擦角為φ，巖土體重度為γ，開挖影響系數為α，則開挖影響區范圍見式（1）。

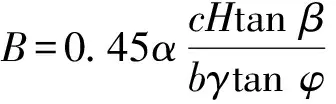
（1）

2 邊坡彈性應力計算及應用

2.1 邊坡坡體內部彈性應力計算

邊坡內部應力狀態可采用彈性理論中楔形體應力分布情況進行模擬計算，如圖3所示。

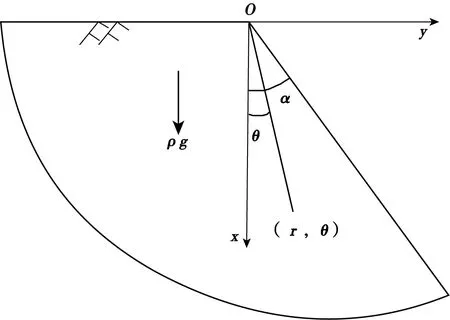
圖3 邊坡頂面水平時邊坡內部應力計算Fig.3 Calculation of the internal stress of the slope when the top surface of the slope is horizontal

設邊坡巖土體密度ρ，根據彈性理論，當邊頂面水平時，在自重作用下邊坡內部應力用式（2）計算。

（2）

如果角度在x軸左邊，則以負值代入。邊坡內部應力分布如圖4所示，在進行邊坡應力分析及邊坡設計時，希望得到沿坡面BC法線及沿坡面方向的應力分布。但式（2）是通過極坐標計算，為應用方便，需將計算結果加以轉化。

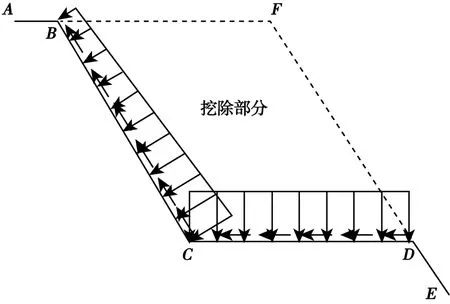
圖4 邊坡內部應力分布Fig.4 Internal stress distribution of slope

鑒于篇幅，本文僅列出轉化結果，建立not坐標系，n方向為邊坡坡面法線方向，t方向為邊坡坡面方向，邊坡傾角為β，如圖5所示。

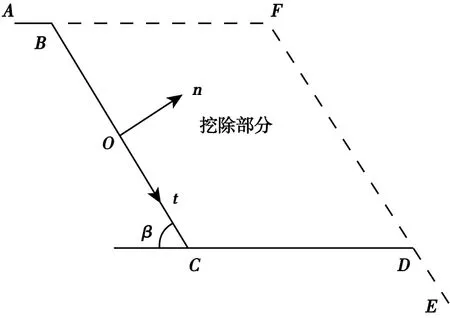
圖5 邊坡應力坐標轉化Fig.5 Slope stress coordinate conversion

經推導，得到邊坡法向及切向應力，見式（3）。

（3）

2.2 邊坡彈性應力計算結果應用

對于理想彈性材料，材料在某一瞬時應變完全取決于該瞬時材料所受外力（溫度不考慮），而與加載歷史、加載順序無關。但巖土體不屬于理想彈性體，彈性理論應用于巖土體時應加以修正。巖土材料回彈—再壓縮曲線如圖6所示。巖土材料再壓縮過程與壓縮過程是不同的，只有經歷過卸載點b后，再壓縮曲線與壓縮曲線相同。

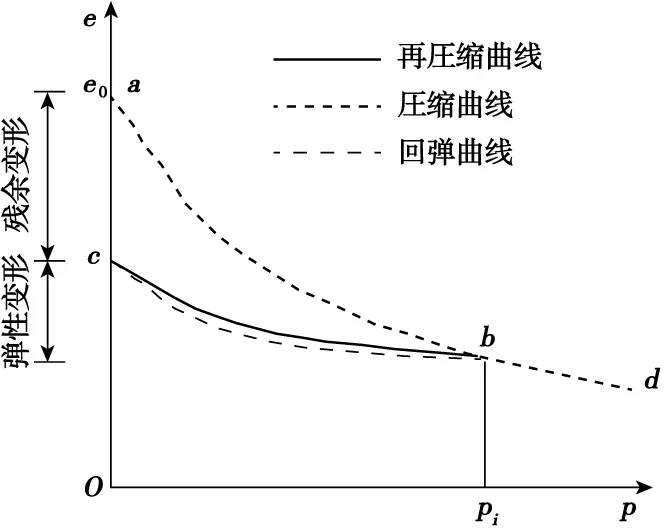
圖6 土的回彈—再壓縮曲線Fig.6 Soil rebound-recompression curve

為了解巖土體與理想彈性材料之間區別，建立如下模型：假設在邊坡上施加一荷載，該荷載使坡體內部巖土體加載后的狀態與未開挖時坡體內部（邊坡線以內）的狀態一致。圖6中，令其對應于b點，然后卸載，卸載過程中，巖土體將產生膨脹，對應于回彈曲線，即圖6中bc段；卸載完成后，巖土體處于c點所對應的狀態，實際上這個過程就是開挖影響區形成的過程。顯然，要回到b點狀態，就要對巖土體進行再壓縮，如果能獲得b點及c點巖土相應壓縮參數，便可計算出從c點到b點所需施加的外荷載，也就是邊坡防護所需提供的抗力。從理論上講，上述分析的方法是相對嚴密的，但要想獲得2個狀態的物理參數，然后進行計算和設計，運用上很不方便。為使應用方便，采用簡化計算方法，即假定解除應力和防護提供的應力一致時，邊坡內部經過應力調整，將重新恢復到原來狀態，同時考慮原邊坡所處狀態各有不同，在此基礎上考慮一定安全系數，即采用式（4）的防護設計。

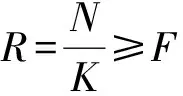
（4）

式中，R為邊坡設計防護能力；N為邊坡計算防護能力；K為安全系數；F為邊坡坡面彈性作用力。

在進行邊坡防護設計時，可按式（4）計算防護能力，進而選用相應的防護形式。當然，防護的抗力提供部分應位于邊坡開挖影響范圍以下一定距離。在實際計算中，可利用式（1）確定相應影響區范圍，而抗力提供部分（錨固部分）起算位置則位于影響區下方1.5～2.0 m處。

2.3 應用條件

應用邊坡內部彈性應力進行邊坡設計時，由于計算公式是在一定假定前提下推導的，公式的應用有一定限制，有關應用條件如下。

（1）邊坡構成材料相對均勻，在一定厚度范圍內，材料變化不大。計算邊坡坡體內部巖土體組成結構單一，如全土質邊坡、全巖質邊坡。實際上，任何邊坡巖土體都是在漫長的沉積而成的，經過各種地質作用，形成不同的土巖組合，在一定尺度范圍內組成邊坡的土質類別單一，可利用上述理論。對于土巖組合邊坡、軟硬巖互層以及其他存在明顯結構面的邊坡而言，滑動位置一般都是沿結構面軟弱位置，其邊坡防護設計也是明確的，無需復雜的計算。

（2）邊坡頂面水平。實際上，這個應用條件僅針對式（2）是在坡頂面水平情況下導出。對于邊坡坡頂面為傾斜時，如圖7所示。

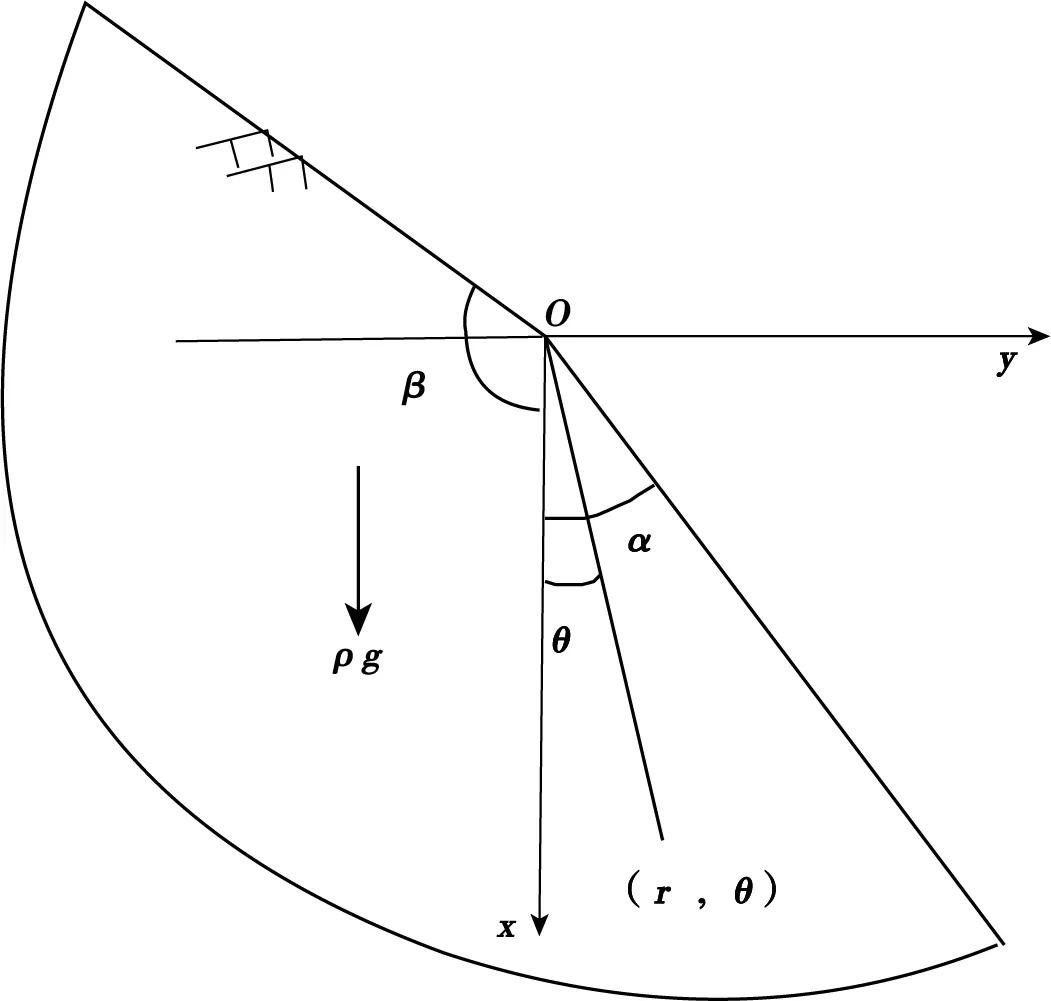
圖7 邊坡坡面傾斜時彈性應力計算Fig.7 Calculation of elastic stress when slope is inclined

相應計算公式要進行調整，可按式（5）計算：

（5）

式中，A、B、C、D為系數，計算相對復雜，與巖土體的密度ρ、傾角β和α的值有關，但可編制成相關計算表格進行計算，見表1。

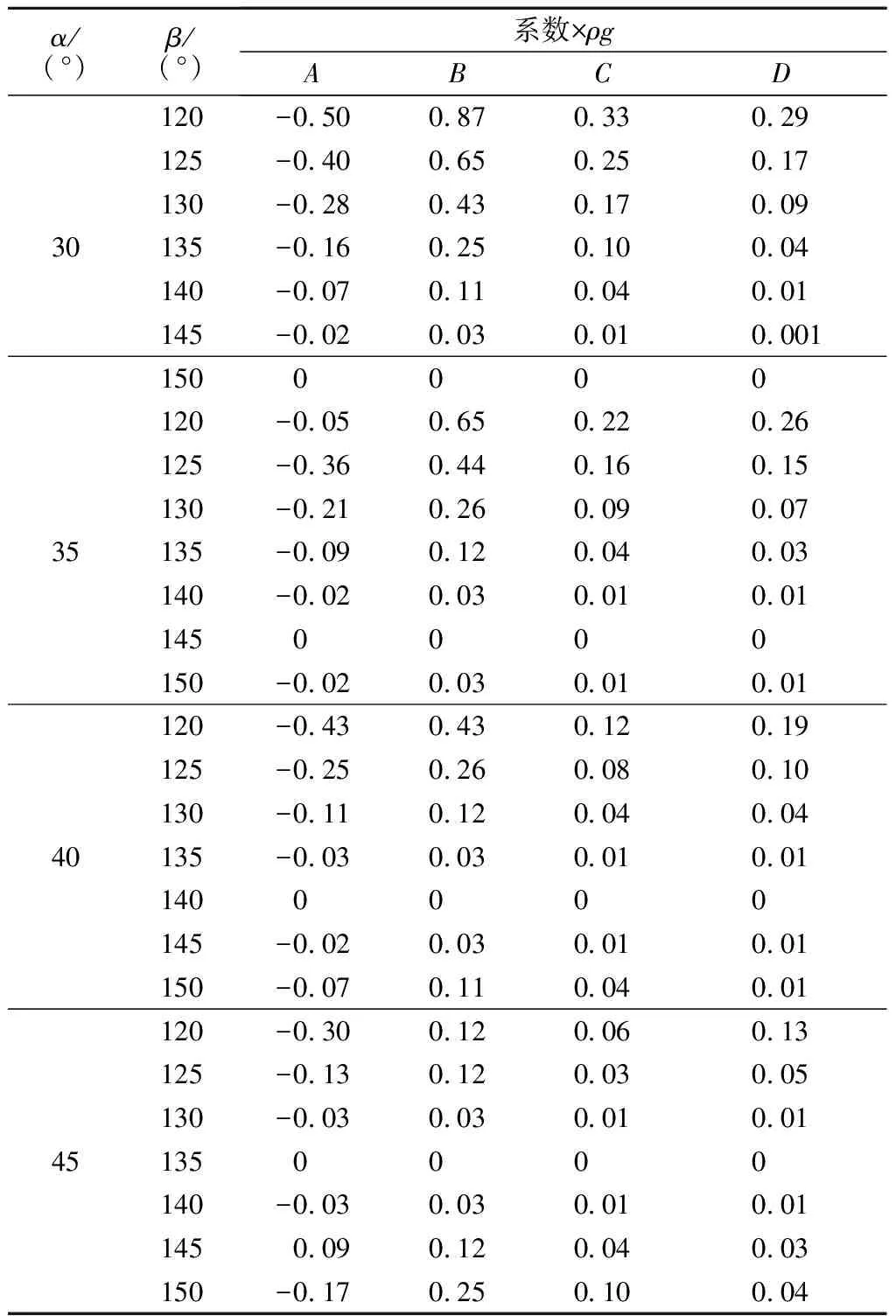
表1 彈性應力計算系數Tab.1 Elastic stress calculation coefficient

3 邊坡穩定性分析

3.1 計算模型

根據工程地質資料，選擇3個典型剖面作為邊坡穩定性分析的計算剖面，平面位置如圖8所示。

3.2 計算參數及工況

（1）計算參數。計算參數的選取主要依據現場及詳勘報告，并結合當地工程經驗值而綜合確定。抗剪強度指標采用直接剪切指標，具體見表2。

（2）計算工況。根據項目場地的工程地質條件，考慮當地氣候條件，邊坡穩定性分析采用3種工況進行計算，分別為天然工況、暴雨工況和暴雨+地震工況。對于地震作用，根據 GB 18306—2015《中國地震動參數區劃圖》，項目場地抗震設防烈度為7度，設計基本地震加速度值為0.10g。同時，考慮場地內人群荷載、車輛荷載、建筑物等荷載作用，在邊坡穩定性計算中假定坡頂范圍內存在180 kPa的分布荷載。

圖8 設計計算模型Fig.8 Design calculation model

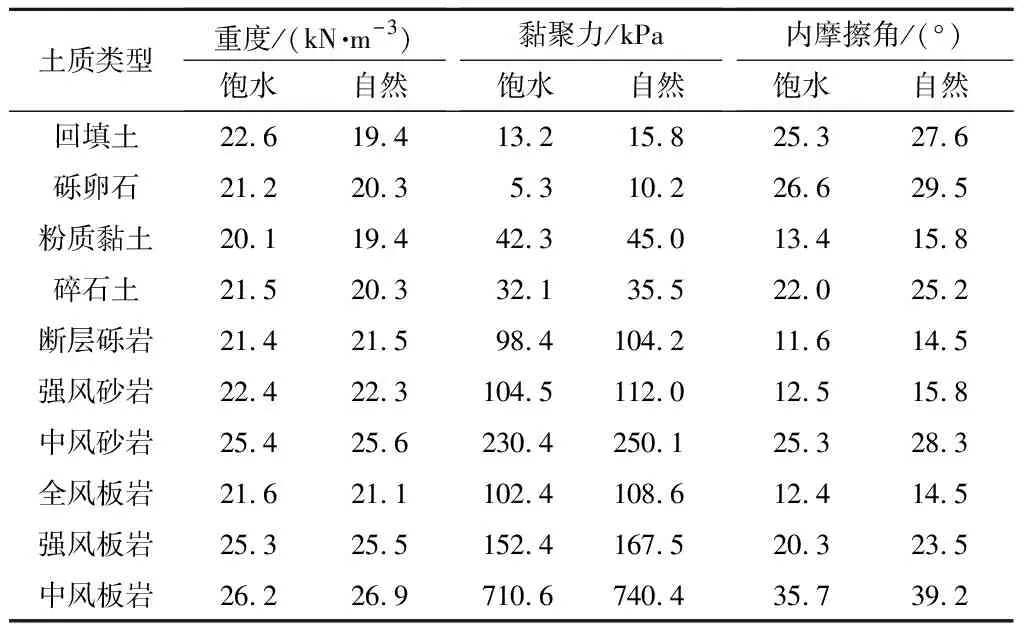
表2 巖土參數建議值Tab.2 Recommended geotechnical parameters

3.3 結果分析

結合彈性理論分析邊坡基于不同工況下的穩定性[9-10]，獲得邊坡穩定安全系數見表3。

表3 邊坡穩定安全系數結果比較Tab.3 Comparison of results

以1-1剖面為例，邊坡在不同工況下的最危險滑動面如圖9所示。

圖9 1-1剖面不同工況下最危險滑動面Fig.9 The most dangerous sliding surface of 1-1 section under different working conditions

根據GB 51254—2017《高填方地基技術規范》要求，填筑邊坡在天然工況、暴雨工況和暴雨+地震工況下的穩定計算安全系數，應分別不小于1.30、1.15、1.05。通過分析可知，3個典型剖面在3種工況下的安全系數均滿足規范要求的穩定安全系數值。在3種計算工況下，邊坡最危險滑動面均穿過填土層，屬于深層滑動，說明采用土工格柵加筋處理后，有效減少了邊坡坡面發生局部破壞的可能性，在一定程度上提高了邊坡整體穩定性。

3.4 邊坡變形監測結果分析

填方邊坡施工完成后，在邊坡坡面布置4 個變形監測斷面，共計14個變形監測點。經分析，各監測點反映的規律類似，因此，以B1J02號監測點為例，對邊坡坡面水平位移和豎向位移變化情況進行分析說明。監測點位移變化曲線如圖10所示，位移變化速率曲線如圖11所示。

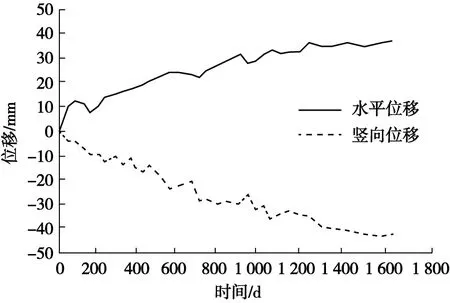
圖10 B1J02 監測點位移變化曲線Fig.10 Displacement curve of monitoring point B1J02

由圖10、圖11可知，填方邊坡最大累計水平位移量為37.3 mm，水平位移變化速率為0.03 mm/d；最大累計垂直位移量為43.0 mm，垂直位移變化速率為-0.04 mm/d。即邊坡施工完成后，隨著時間的延長，B1J02號監測點水平及豎向變形減緩并逐漸收斂，說明填方邊坡變形已趨于穩定，邊坡整體穩定性良好。

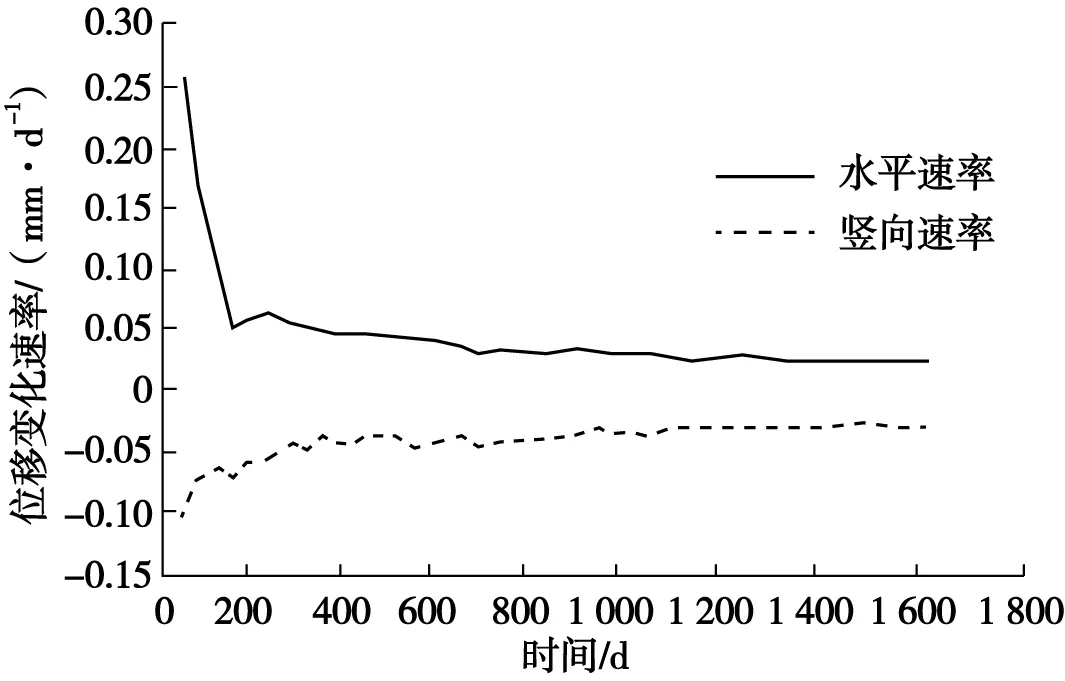
圖11 B1J02 監測點位移變化速率曲線Fig.11 Displacement change rate curve of monitoring point B1J02

4 結語

邊坡工程是巖土工程中一個重要分支，幾乎所有巖土工程都要涉及到巖土邊坡開挖、防護。本文將彈性理論的相關解答引入到邊坡工程中，旨在為邊坡防護設計提供一種新的思路。應該指明，采用此種方法進行邊坡防護設計，目前應用得還不多，從工程安全的角度出發，設計人員可采用此種方法設計，并與傳統設計方法類比，積累經驗以供參考。高填方邊坡工程技術難度大，邊坡穩定性對工程建設的安全具有較大的影響，在設計施工時應引起足夠重視。