跨座式單軌弓網(wǎng)耦合魯棒主動控制策略
劉朝濤,藍(lán)立俊,杜子學(xué),楊震
(重慶交通大學(xué)機(jī)電與車輛工程學(xué)院,重慶400074)
0 前言
重慶市跨座式單軌列車屬于城市軌道交通的一種新型形式,對于其他制式的軌道交通,跨座式單軌交通有其獨(dú)特的機(jī)械結(jié)構(gòu)和驅(qū)動原理。跨座式單軌列車隨著運(yùn)行速度的增加,弓網(wǎng)之間容易產(chǎn)生振動以致接觸力大幅波動。接觸力過大容易使弓網(wǎng)間的摩擦增大,造成設(shè)備間磨耗加劇,嚴(yán)重時會出現(xiàn)其他安全事故;過低的接觸力容易造成弓網(wǎng)分開的離線現(xiàn)象,所產(chǎn)生的電弧和火花對相關(guān)的電氣器件會產(chǎn)生燒蝕,對信息通信造成干擾。因此,對于受電弓進(jìn)行主動控制以降低接觸力波動具有很大的意義,同時也是軌道交通電氣化發(fā)展不可或缺的一部分。
基于跨座式單軌列車的設(shè)計特殊性,國內(nèi)外對于單軌受電弓的研究不是很多,但是對于高速鐵路受電弓的主動控制已有大量的研究,所以文中借鑒了高速鐵路受電弓主動控制的研究方法。文獻(xiàn)[2]提出了一種基于估計器的主動雙受電弓H控制策略,在得到受電弓狀態(tài)的基礎(chǔ)上,用了一種魯棒遞推狀態(tài)估計方法,可以有效地處理隨機(jī)缺失測量,以減小接觸力波動。文獻(xiàn)[3]采用了滑模魯棒控制來調(diào)節(jié)弓網(wǎng)的接觸力,其中設(shè)計的滑動模態(tài)控制器是基于輸出調(diào)節(jié)問題的標(biāo)準(zhǔn)滑模控制理論,最后通過仿真實(shí)驗(yàn)驗(yàn)證了設(shè)計的方案。文獻(xiàn)[4]研究了一種多目標(biāo)魯棒主動控制方法,分析引起接觸力波動的因素,以確定3個控制目標(biāo),即最小化集電弓收集器的加速度,限制控制力和位移約束,最后驗(yàn)證了其方法的可行性。文獻(xiàn)[5]提出了一種基于模糊滑模控制器和附加補(bǔ)償器的高速列車受電弓接觸網(wǎng)魯棒控制方法,控制采用了PID外環(huán)反饋,然后由模糊系統(tǒng)在線調(diào)節(jié)滑模項(xiàng)和PID項(xiàng)的增益來控制接觸力的波動,仿真結(jié)果與實(shí)際情況吻合較好。文獻(xiàn)[6]提出了一種基于Pareto集和變權(quán)的受電弓主動懸架參數(shù)優(yōu)化設(shè)計方法,采用約束多目標(biāo)進(jìn)化算法,通過大量的仿真驗(yàn)證了所提出的設(shè)計方案。
本文作者借鑒以上學(xué)者們的研究,針對跨座式單軌受電弓的特點(diǎn),建立了一種主動控制模型,并提出了一種魯棒主動控制方法。在跨座式單軌受電弓底座和框架間安裝有升弓彈簧,為弓網(wǎng)間接觸提供自適應(yīng)力,但升弓彈簧響應(yīng)非常有限。因此,需要加入執(zhí)行機(jī)構(gòu)進(jìn)行主動干預(yù)和調(diào)節(jié)。文中所研究的主動控制是以直流電機(jī)為執(zhí)行機(jī)構(gòu),為了不改變受電弓內(nèi)部結(jié)構(gòu)參數(shù),所以將電機(jī)與框架連桿直連;并且希望在減少傳感器數(shù)量的情況下,通過卡爾曼濾波算法獲得精確度較高的電機(jī)轉(zhuǎn)子狀態(tài)控制信息;最后設(shè)計了魯棒H控制器作為系統(tǒng)整體控制器。整體系統(tǒng)結(jié)構(gòu)如圖1所示。

圖1 系統(tǒng)結(jié)構(gòu)
1 跨座式單軌列車弓網(wǎng)耦合模型
1.1 弓網(wǎng)系統(tǒng)耦合模型的建立
跨座式單軌受電弓主要由底座、框架、弓頭以及受電弓彈簧等部件組成。單軌受電弓在結(jié)構(gòu)上與其他制式的受電弓有較大的差別,但是在工作模式和動態(tài)特性上有相似之處。所以在分析單軌受電弓的動力學(xué)模型時,可以參照現(xiàn)有的方法進(jìn)行。考慮到弓網(wǎng)動態(tài)耦合時,接觸力的波動范圍不大,因此,可以對受電弓的動力學(xué)模型進(jìn)行線性化處理。
跨座式軌道交通弓網(wǎng)耦合系統(tǒng)不同于其他的軌道交通的弓網(wǎng)耦合系統(tǒng),接觸網(wǎng)是通過錨段關(guān)節(jié)連接每一段伸縮單元并固定在軌道梁的側(cè)壁,而受電弓則是橫向安裝在軌道列車的底部裙板,弓網(wǎng)耦合系統(tǒng)為橫向剛性接觸受流。所以,重力和空氣阻力都可以忽略不計。
由于弓網(wǎng)接觸為剛性接觸,理論上是不存在彈性形變的,但是在振動的影響下,接觸線和匯流排的整體會產(chǎn)生一定的彈性變形,因此在建模時要考慮接觸網(wǎng)的彈性特性。同時,為了方便建模,將支持絕緣子視為剛體,并且假設(shè)接觸網(wǎng)每個跨距都是均勻的,且跨距之間的過渡段光滑無硬點(diǎn)。最后將受電弓框架部分以及弓頭部分看作單獨(dú)的質(zhì)量塊,它們之間以等效的剛度和阻尼相連,因此得到了簡化的弓網(wǎng)耦合模型如圖2所示。

圖2 弓網(wǎng)耦合動力學(xué)模型
可以得到弓網(wǎng)耦合系統(tǒng)的運(yùn)動微分方程為
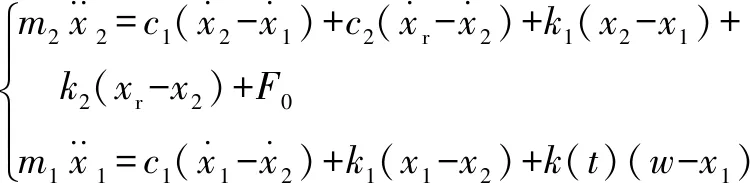
(1)
式中:()為接觸網(wǎng)的等效剛度;為靜態(tài)抬升力;為接觸網(wǎng)不平順以及振動產(chǎn)生的激勵;為列車振動產(chǎn)生的激勵。
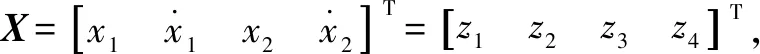
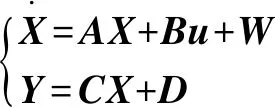
(2)
其中:
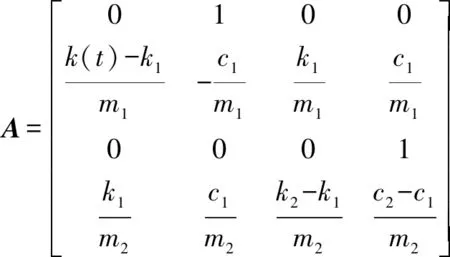

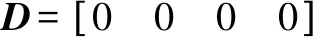

基于此,整個系統(tǒng)的問題可以轉(zhuǎn)化為設(shè)計一個弓網(wǎng)接觸力()反饋律的問題:
()=()
(3)
其中:是控制增益矩陣。受電弓的魯棒控制問題是確定滿足以下要求的控制增益矩陣:
(1)閉環(huán)系統(tǒng)是漸近穩(wěn)定的;
(2)當(dāng)外部擾動不大于時,控制目標(biāo)得到保證。
1.2 弓網(wǎng)系統(tǒng)耦合模型的仿真分析
跨座式單軌列車的軌道由預(yù)應(yīng)力混凝土梁組成,正、負(fù)的鏈節(jié)沿預(yù)應(yīng)力混凝土梁的兩側(cè)剛性安裝。由于跨座式單軌列車中特殊的受電弓與接觸網(wǎng)之間的耦合關(guān)系,導(dǎo)致跨座式單軌還沒有集電質(zhì)量標(biāo)準(zhǔn)。但是根據(jù)鐵路標(biāo)準(zhǔn)TB/T 3271—2011、重慶跨座式單軌運(yùn)行的經(jīng)驗(yàn),以及杜子學(xué)團(tuán)隊對單軌受電弓所研究的結(jié)果,給出了跨座式單軌的集電質(zhì)量參考標(biāo)準(zhǔn)。
跨座式單軌的受電弓與接觸網(wǎng)之間的接觸力在整個工作行程中應(yīng)在44~79 N內(nèi)。因此,受電弓與接觸網(wǎng)的最大接觸力應(yīng)小于79 N,受電弓與接觸網(wǎng)的最小接觸力應(yīng)大于44 N。 接觸力的標(biāo)準(zhǔn)差直接反映了接觸力的波動范圍,標(biāo)準(zhǔn)差越小,接觸力的波動范圍越小,集電質(zhì)量越好。
弓網(wǎng)系統(tǒng)中,靜抬升力=100 N,升弓彈簧剛度和阻尼系數(shù)為=12 900 N/m、=100 N·m·s/rad;弓頭支座的橡膠彈簧剛度和阻尼系數(shù)參數(shù)為=17 000 N/m、=200 N·s·m/rad,接觸剛度為()=73 200 N/m,弓頭以及框架的等效質(zhì)量=2.354 kg、=10.647 kg;對于外部激勵的功率參數(shù)可以參考日本剛性懸掛接觸網(wǎng)不平順功率譜密度函數(shù)。文中由此對弓網(wǎng)耦合模型進(jìn)行了Simulink建模仿真,并且在40、60、80 km/h時速段進(jìn)行了弓網(wǎng)接觸力的時域響應(yīng)圖分析,如圖3所示。

圖3 不同時速下的接觸力響應(yīng)曲線
由圖3分析可以統(tǒng)計出不同時速下的接觸力,如表1所示。
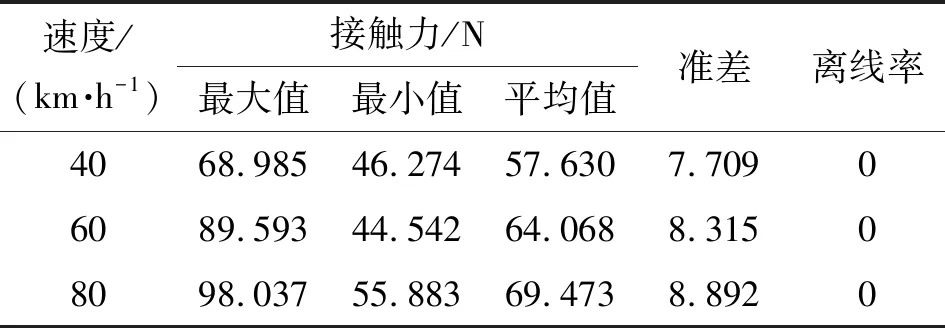
表1 不同時速的接觸力數(shù)據(jù)統(tǒng)計
由圖3可知:列車在40 km/h運(yùn)行時,接觸力的變化是比較平緩的,集中在45~70 N之間,受電弓屬于最佳的受流區(qū)間;但是隨著速度的增加,列車在60 km/h運(yùn)行時,接觸力的變化較為劇烈,大多數(shù)集中在50~85 N之間,脫離了受電弓最佳的受流區(qū)間;列車在80 km/h運(yùn)行時,弓網(wǎng)之間的接觸力變化最不穩(wěn)定,所以需要在列車高速時對受電弓進(jìn)行主動干預(yù),讓接觸力的波動有所減小,以降低弓網(wǎng)接觸力。
2 直流電機(jī)模型與控制器設(shè)計
永磁無刷直流電機(jī)在工業(yè)領(lǐng)域越來越受歡迎,因?yàn)榕c其他類型的交流和直流電機(jī)相比,它具有更高的功率密度、更簡單的制造工藝、更低的生產(chǎn)成本和響應(yīng)時間快等顯著優(yōu)勢。
2.1 永磁直流電機(jī)模型的建立
標(biāo)準(zhǔn)的三相直流電機(jī)系統(tǒng)可以用方程在狀態(tài)空間中表示:
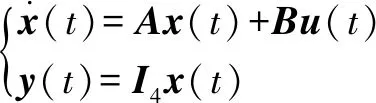
(4)
其中:是4×4的單位矩陣,其余變量為
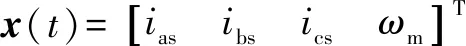

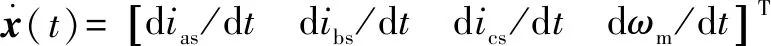

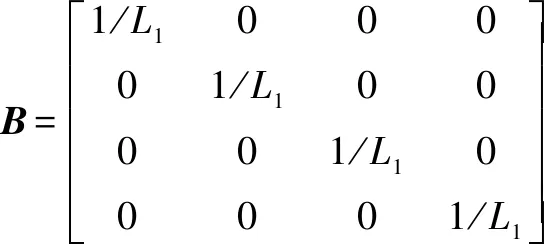
式中:、和是直流電機(jī)定子繞線的相電流;是角速度;、和是每相的電壓輸入;是機(jī)械負(fù)載的扭矩;是每相電阻;=-,其中是所有三相共有的每相自感,是相之間的公共互感;是轉(zhuǎn)動慣量;是扭矩常數(shù);是速度常數(shù)。永磁直流電機(jī)在三相之間以共同的電流和電壓運(yùn)行,即:===,===。
2.2 逆變器模型的建立
此系統(tǒng)采用H全橋作為三相逆變電路,它主要是由6個對稱的MOSEFT管構(gòu)成,如圖4所示。

圖4 逆變器拓?fù)?/p>
當(dāng)直流電機(jī)ab相導(dǎo)通時,=0,可得:
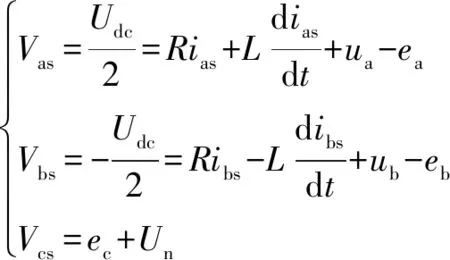
(5)
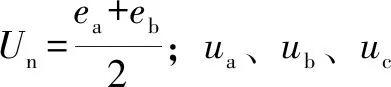
電機(jī)在換向的時候,c相導(dǎo)通,不為0,會產(chǎn)生反向電動勢,則:

(6)
是直流側(cè)的電壓,通過逆變器,結(jié)合電感電動勢可以得到輸出至三相繞組的端電壓。
2.3 卡爾曼濾波算法
電機(jī)在換向時存在反向電動勢會產(chǎn)生系統(tǒng)頻率噪聲,這對電機(jī)的響應(yīng)時間有影響,于是文中提出一種卡爾曼濾波算法來實(shí)時檢測電機(jī)轉(zhuǎn)子的位置以調(diào)整電機(jī)的響應(yīng)時間。該算法是根據(jù)電機(jī)主動控制系統(tǒng)中容易得到的相電流和相電壓等信號,利用卡爾曼濾波算法對電機(jī)系統(tǒng)參數(shù)進(jìn)行在線估計,得到轉(zhuǎn)子的位置,以便縮短電機(jī)的響應(yīng)時間。該算法已經(jīng)考慮了系統(tǒng)參數(shù)誤差和干擾,所以這種算法對系統(tǒng)外部干擾有強(qiáng)適應(yīng)性。為了表述整個過程,可以由下式表示:
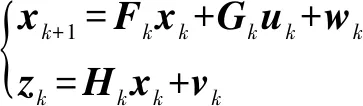
(7)
其中:、、為相關(guān)系數(shù)矩陣;表示過程噪聲;表示測量噪聲。它們都是不相關(guān)的零均值高斯白噪聲,它們的協(xié)方差矩陣是和。
卡爾曼濾波算法的一個周期有2個主要階段:預(yù)測和更新。預(yù)測步驟使用來自前一時間步的狀態(tài)估計來產(chǎn)生當(dāng)前時間步的估計,這種預(yù)測狀態(tài)估計也稱為先驗(yàn)狀態(tài)估計。在更新階段,當(dāng)前先驗(yàn)預(yù)測與當(dāng)前觀測相結(jié)合,用于將狀態(tài)估計細(xì)化為后驗(yàn)狀態(tài)估計。其中,預(yù)測階段為預(yù)測狀態(tài)及其協(xié)方差估計的計算:

(8)
更新階段為測量誤差及其協(xié)方差的計算:
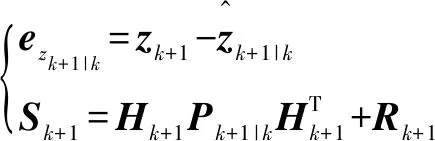
(9)
然后,最佳卡爾曼增益的計算:
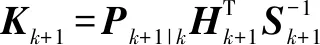
(10)
最后,更新狀態(tài)及其協(xié)方差估計的計算:
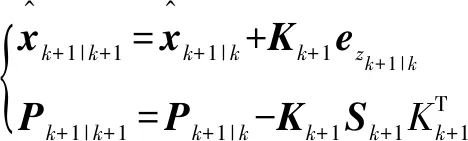
(11)
卡爾曼濾波算法是一種有效的高斯過程最優(yōu)濾波算法。當(dāng)對象模型足夠精確時,性能更好;但當(dāng)模型存在誤差時,這種增長記憶濾波器使得“舊的”測量數(shù)據(jù)對當(dāng)前狀態(tài)會產(chǎn)生發(fā)散的影響。
2.4 魯棒H∞控制器的設(shè)計
在設(shè)計魯棒H控制器的階段,需要一個面向控制的模型,該控制策略的主要目標(biāo)是在不影響弓網(wǎng)接觸力平均值的情況下減少接觸力的波動。通過將參考值作為干擾可以將其視為跟蹤問題。因此,可以通過最小化實(shí)時接觸力與參考值之間的差異來實(shí)現(xiàn)控制目標(biāo):
min[()]=min[-()]
(12)
其中:()為跟蹤誤差;為參考值;()為實(shí)時接觸力。
給定正標(biāo)量和,使得存在適當(dāng)維數(shù)矩陣的正定對稱矩陣>0和普通矩陣,并且滿足以下矩陣關(guān)系:
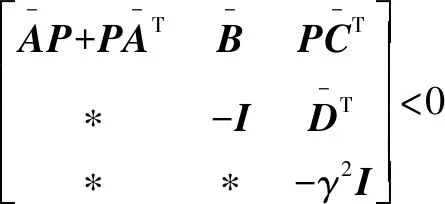
(13)

(14)
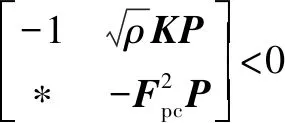
(15)
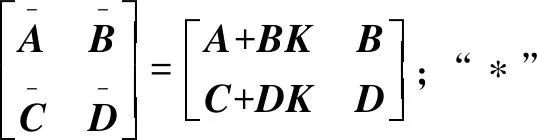
=
(16)
結(jié)合主動控制模型,受電弓主動控制力可以表示為

(17)
3 仿真實(shí)驗(yàn)分析
3.1 電機(jī)系統(tǒng)參數(shù)的設(shè)置
對于永磁直流電機(jī),系統(tǒng)參數(shù)設(shè)置如下:扭矩常數(shù)=25.1 mN·m/A,速度常數(shù)=380 r/(min·V),每相電阻=0.454 Ω,轉(zhuǎn)動慣量=135 g·cm,每相的電感=0.322 mH,阻尼系數(shù)=0.000 2 N·m·s/rad,極對數(shù)=2,電源為直流220 V。
H控制器的有效性和魯棒性通過一個線性控制模型可以得到驗(yàn)證。控制增益矩陣參數(shù)計算如下:
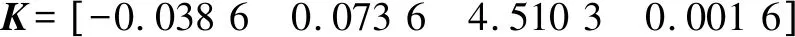
3.2 實(shí)驗(yàn)仿真結(jié)果分析
根據(jù)弓網(wǎng)模型的參數(shù)和電機(jī)系統(tǒng)參數(shù),進(jìn)行了Simulink仿真實(shí)驗(yàn),對控制策略進(jìn)行了評估,如圖5所示。
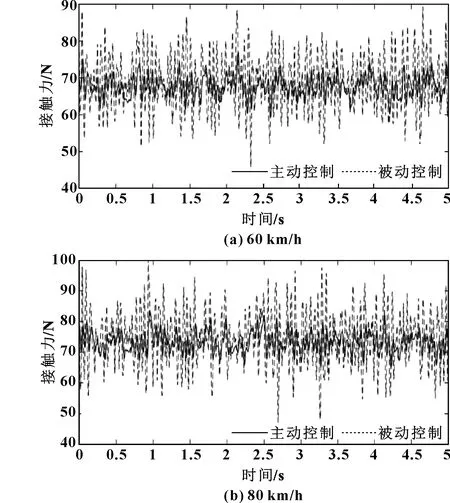
圖5 不同時速下的接觸力響應(yīng)曲線
由表2可知:在弓網(wǎng)耦合系統(tǒng)中加入了魯棒H控制器主動控制策略,在60和80 km/h的速度下,最大接觸力的值分別下降了16%和15%,最小接觸力的值分別上升了50%和44%;在60和80 km/h的速度下,標(biāo)準(zhǔn)差分別降低了9%和8%。但是在80 km/h的速度下,控制的效果沒有那么明顯,原因是電機(jī)的響應(yīng)速度一定,單軌列車隨著速度的增加,對高頻的信號愈發(fā)敏感。
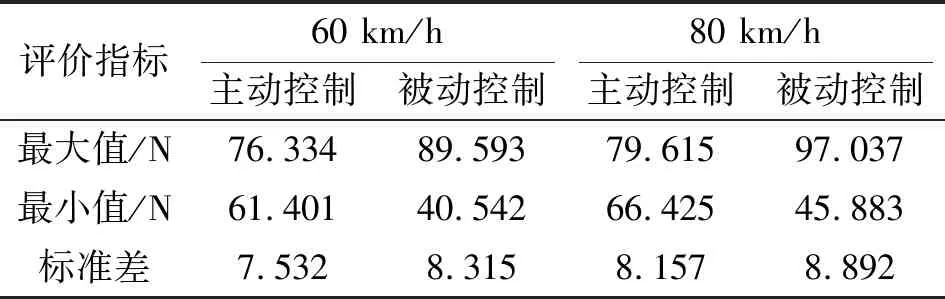
表2 不同時速下弓網(wǎng)受流質(zhì)量評價指標(biāo)統(tǒng)計
如圖6所示是80 km/h時速下質(zhì)量塊和位移曲線。
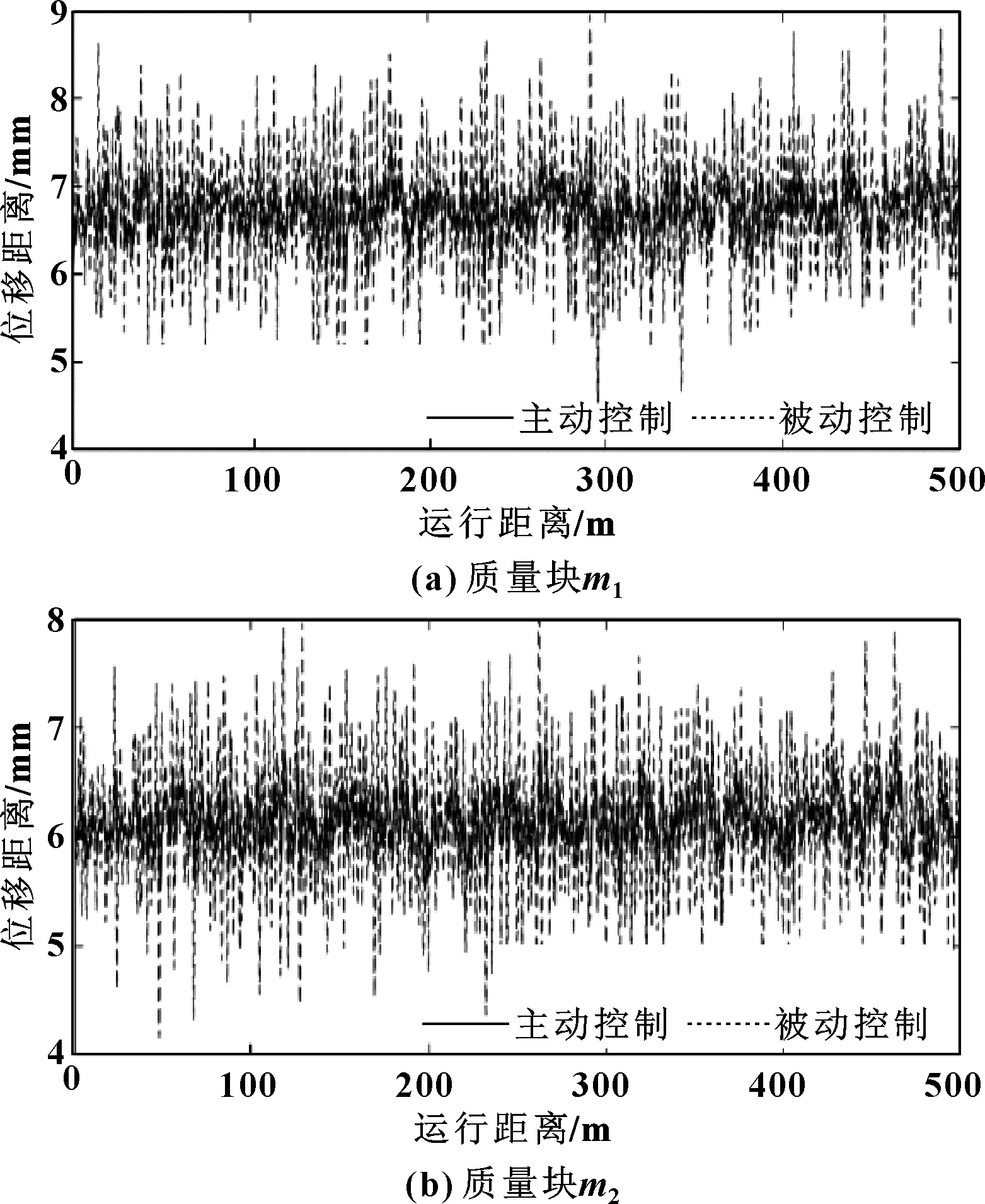
圖6 80 km/h時速下位移曲線
圖7所示是實(shí)測重慶市軌道三號線雙龍至碧津在80 km/h時速下,受電弓弓頭的頻率響應(yīng)曲線。可知:弓頭振動的頻率集中在0~25 Hz以內(nèi),并且主要頻率成分小于13 Hz左右,這能反映出弓網(wǎng)系統(tǒng)的低頻振動特性,同時電機(jī)主動控制的反應(yīng)速度也符合這頻段所產(chǎn)生的激勵。
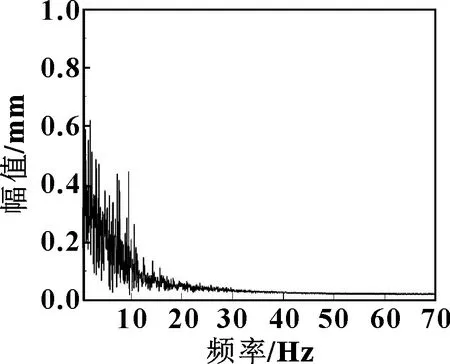
圖7 80 km/h時速下弓頭頻特曲線
4 結(jié)論
本文作者提出了一種基于魯棒H控制器的受電弓主動控制策略,用于減小弓網(wǎng)接觸力的波動。首先借鑒了高速鐵路的主動控制方法,建立了一種二自由度的主動控制模型,以直流電機(jī)作為執(zhí)行機(jī)構(gòu)進(jìn)行弓網(wǎng)接觸力的調(diào)節(jié);然后根據(jù)直流電機(jī)的相電流和相電壓等信號,利用卡爾曼濾波算法對電機(jī)轉(zhuǎn)子位置進(jìn)行估計;最后在魯棒H控制器的作用下,弓網(wǎng)系統(tǒng)的接觸力得到了有效的控制。
研究結(jié)果表明:該控制策略有效降低了弓網(wǎng)接觸力的波動,減小了標(biāo)準(zhǔn)差。在60和80 km/h的速度下,分別降低了9%和8%。總體來說,該控制策略相比現(xiàn)有的控制策略突出的地方在于:采用了卡爾曼濾波算法對電機(jī)轉(zhuǎn)子位置進(jìn)行了估計,對電機(jī)給出了一種更有效的估計方法。最后,所有的這些結(jié)論都通過大量的實(shí)驗(yàn)進(jìn)行仿真,進(jìn)一步驗(yàn)證了所設(shè)計的主動控制策略的有效性和魯棒性。

