激勵因素對人字齒行星齒輪系統動態特性的影響
林何,李瑞華,孟漁航
(1.西安工程大學機電工程學院,陜西西安 710084;2.西安工程大學,西安市現代智能紡織裝備重點實驗室,陜西西安 710600)
0 前言
人字齒行星齒輪作為大功率、高轉速傳動形式的一種,被廣泛應用于風電、航空航天、船舶重工等工業傳動領域。隨著人字齒行星齒輪應用范圍的擴展和性能需求的提高,影響系統振動不均的因素越來越受到重視。為了改善人字齒行星齒輪傳動系統的動載穩定性,國內外學者不斷提出新的方法或技術對人字齒行星齒輪傳動的動態特性進行研究。WEI等提出了一種利用虛擬等效軸單元的動力學建模方法,構建了人字齒行星齒輪系統的動力學模型。MO等基于集中參數理論和Lagrange方法建立了人字齒行星傳動系統的動力學模型。李同杰等建立了直齒行星齒輪傳動純扭轉動力學模型,分析了激勵頻率、齒側間隙對該系統動力學特性的影響。但行星齒輪系在嚙合傳動過程中各齒輪的動載特性還會受到阻尼、綜合嚙合誤差和時變嚙合剛度等因素的影響。WANG和WU以風電減速箱行星齒輪傳動系統的純扭轉非線性動力學模型為研究對象,對比并分析了不同阻尼比對該系統動力學特性的影響,但是沒有涉及其他激勵因素對振動的影響。國內研究人員還分析了嚙合相位對行星齒輪傳動系統動力學特性的影響,發現嚙合相位差越小行星齒輪系統的平移振動越小。這些研究主要集中于單個因素對系統動態特性的分析。人字齒齒輪在結構上可視為2對斜齒齒輪的組合體,獨特的結構特性使其在嚙合過程中同時存在多點嚙合和多源激勵的情形,輪齒不斷的接觸和脫離過程中不斷地承受沖擊降低了運動穩定性,對其動載特性的研究對于系統的整體穩定尤為必要。
為進一步探究激勵因素對系統在嚙合過程中動態特性的綜合影響。本文作者建立人字齒行星輪系的純扭轉非線性動力學模型,使用Runge-Kutta法進行數值求解,分析激勵因素對內、外嚙合副動載性能的影響規律,并借助三維速度-頻率掃描瀑布圖、相圖和Poincaré映射研究系統的動態特性,對系統倍周期響應進行分析。
1 動力學模型與求解
人字齒行星齒輪系傳動系統簡圖如圖1所示。行星齒輪系主要包括一個太陽齒輪(s)、多個相同的行星齒輪(p)和一個內齒圈(r),行星齒輪主要由一個行星架(c)通過中間的滾動軸承進行剛性連接。輸入扭矩作用在太陽輪上,輸出扭矩作用在行星架輸出軸上。圖2中-為系統全局坐標系。動力學模型中單個人字齒輪分為左斜齒輪和右斜齒輪,2個斜齒輪之間視為歐拉梁單元銜接。
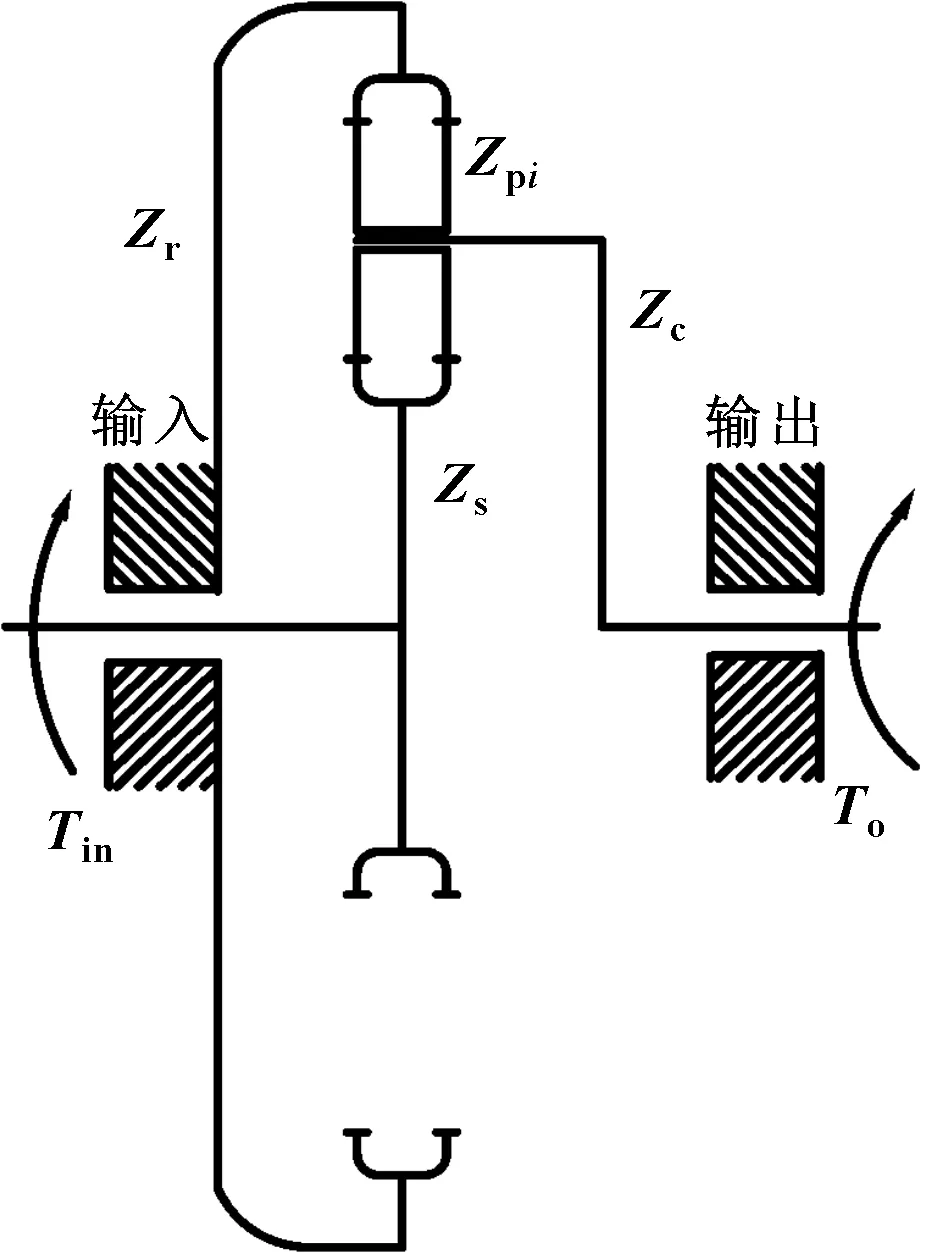
圖1 人字齒行星齒輪系傳動系統簡圖
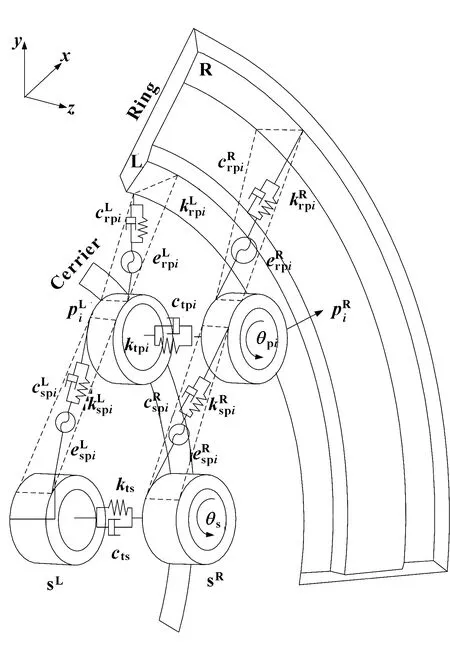
圖2 人字齒行星齒輪系的純扭轉非線性動力學模型
所建動力學模型中作出如下假設:(1)模型中各個轉動體均關于其扭轉中心對稱,各齒輪視為剛體且物理屬性相同。(2)斜齒輪由于接觸的齒對數量波動而導致的嚙合剛度的時變分量被忽略。(3)輪齒滑動產生的摩擦力忽略不計。(4)嚙合線位于嚙合平面內,阻尼力和嚙合力視為嚙合位移函數。不考慮內齒圈的扭轉振動,采用集中質量法建立含間隙人字齒行星齒輪動力學方程組(式(1)):
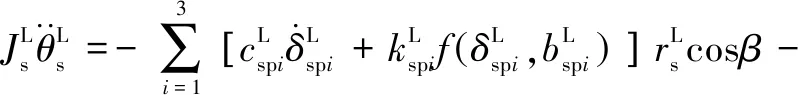
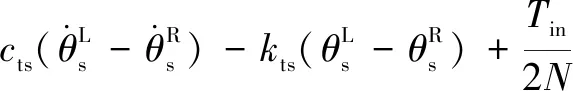
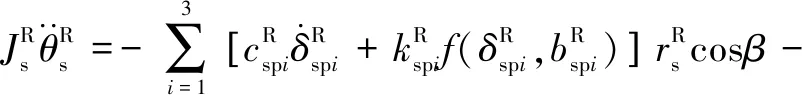
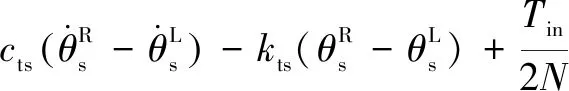
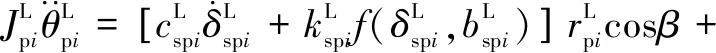
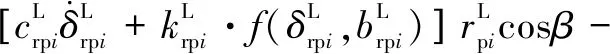

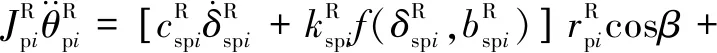
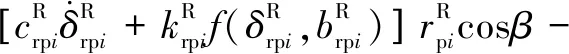
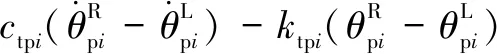
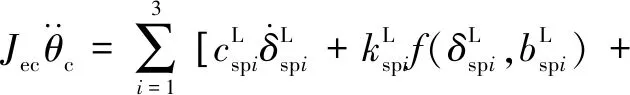
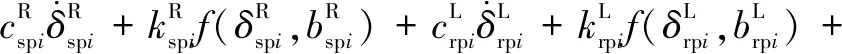
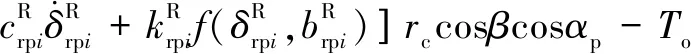
(1)
內齒圈固定,認為內齒圈不產生振動,微分方程數量減1。
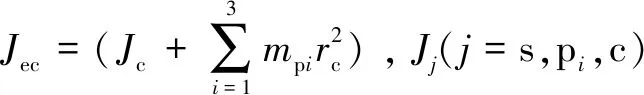
(sp,sp)是非線性間隙函數,具有分段線性特征。為等效實際嚙合傳動,令齒側間隙為2,有:
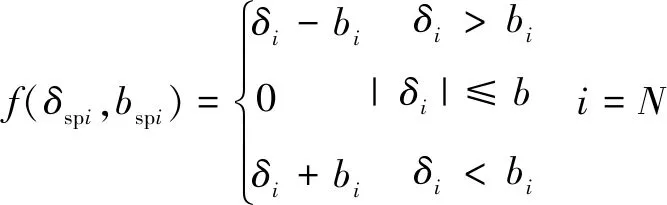
(2)
取= 10 μm。
方程組后續需進行消除剛體位移及量綱一化求解,需將角位移轉變為相應基圓切線上的等價線位移。即
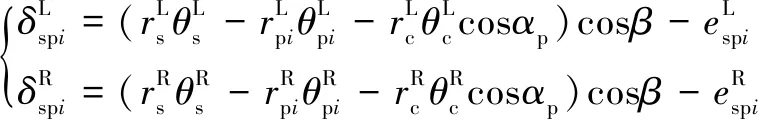
(3)
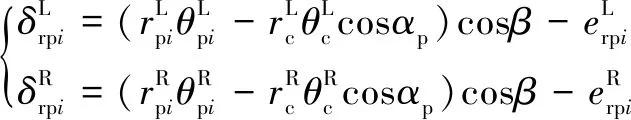
(4)
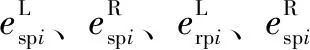
動力學模型中,太陽輪、行星輪和內齒圈可視為兩個斜齒輪通過梁連接,則太陽輪、行星輪和內齒圈在扭轉方向存在剛體位移,使得方程組(1)成為奇異方程組,解不收斂。故引入轉動剛體間的相對位移、p,即
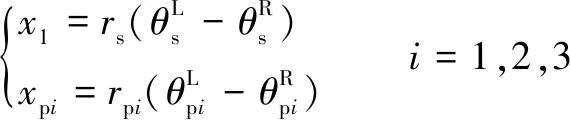
(5)
將式(5)代入式(1),再將方程組(1)代入式(3)和式(4)中消除剛體位移,消去剛體矩陣奇異性,構建新方程組。
在數值計算中,若同一方程中的系數量級相差很大,計算時容易出現病態問題,因此需要對方程組進行量綱一化處理。
定義各構件的等效質量為:=,系統固有頻率為
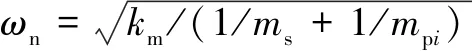
(6)
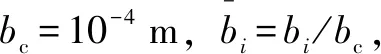
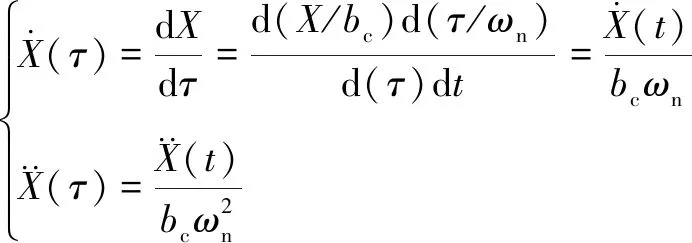
(7)
將未經量綱一化處理的參數代入消剛體位移后的方程組中,進行量綱一化處理,得到不含剛體位移的含有16個自由度的間隙型非線性方程組,整理后統一形式為
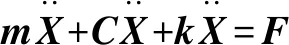
(8)
式中:為量綱一化后的嚙合位移;、、和4個系數矩陣分別為量綱一化后的質量矩陣、阻尼矩陣、剛度矩陣和載荷矢量。其中=[,p,sp,rp],=1,2,3,=1,2,1為左側,2為右側。需要說明的是因系統整體動力學方程復雜,參數較多,故只將內、外嚙合位移sp、rp的阻尼矩陣與剛度矩陣列出,即:
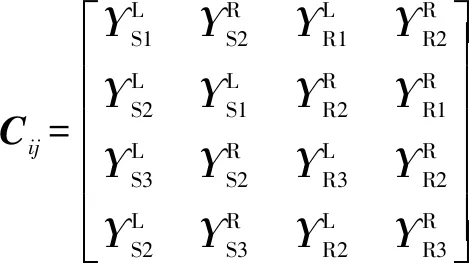
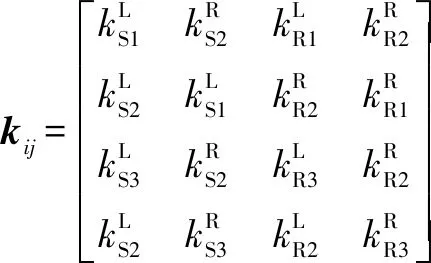
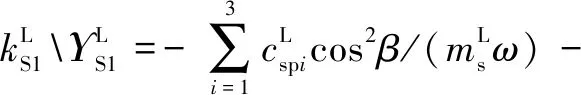
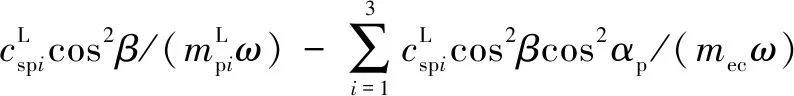
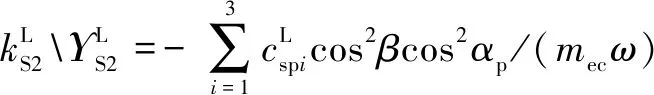
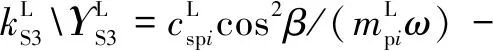
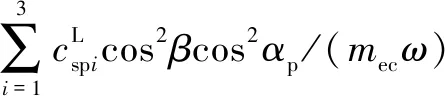
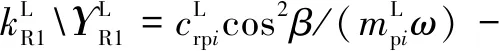
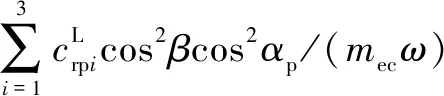
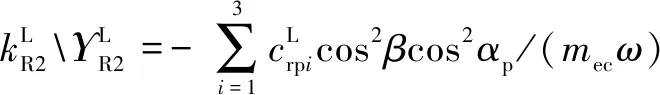
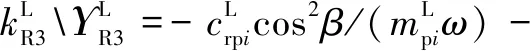
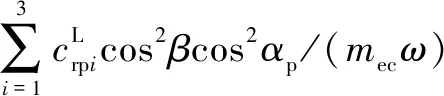
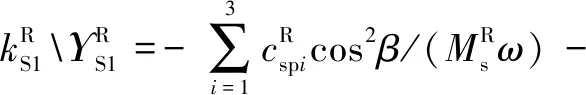
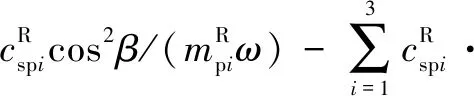
coscos()
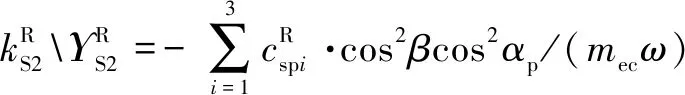
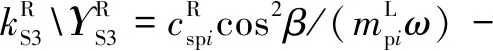
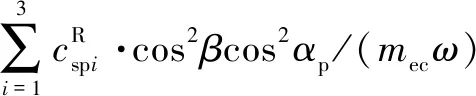
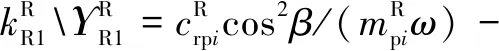
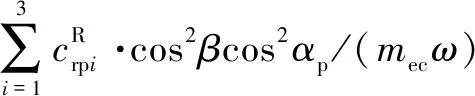
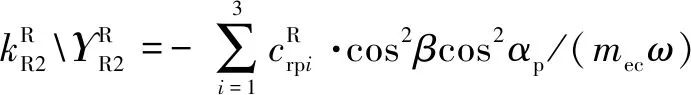
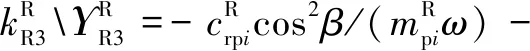
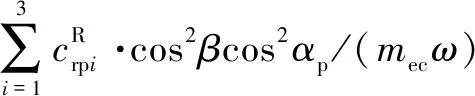
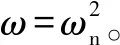
利用Fourier級數展開式表達時變嚙合剛度,則時變嚙合剛度表達式為
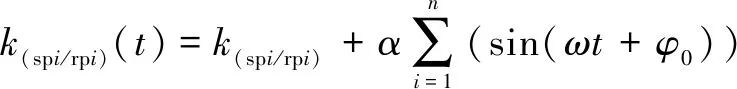
(9)
式中:(sprp)為內、外嚙合副時變嚙合剛度均值;為剛度波動系數;為嚙合頻率;為初相位;=1,2,3。
阻尼根據時變嚙合剛度進行確定,其表達式為

(10)
式中:為阻尼比;(sprp)為內、外嚙合副的等效質量;=1,2,3。
綜合嚙合誤差一般采用簡諧函數描述,即
(sprp)()=(sprp)sin(+(sprp))
(11)
式中:(sp/rp)為各嚙合副綜合嚙合誤差幅值;(sp/rp)為各嚙合副綜合嚙合誤差初相位;=1,2,3。最后對量綱一化后的微分方程組使用Runge-Kutta法進行求解。
2 振動特性
動力學系統中的行星輪數目=3;齒輪兩側斜齒輪的螺旋角=16°,法面壓力角=20°;輸入轉矩=891 N·m;外嚙合的嚙合剛度=8.38×10N/m,內嚙合的嚙合剛度=7.62×10N/m;動力學系統中其余主要物理參數如表1所示,為簡化系統分析計算,人字齒輪左右斜齒輪參數均視為相同。以下所有非線性參數分析均以人字齒左側齒輪為主。
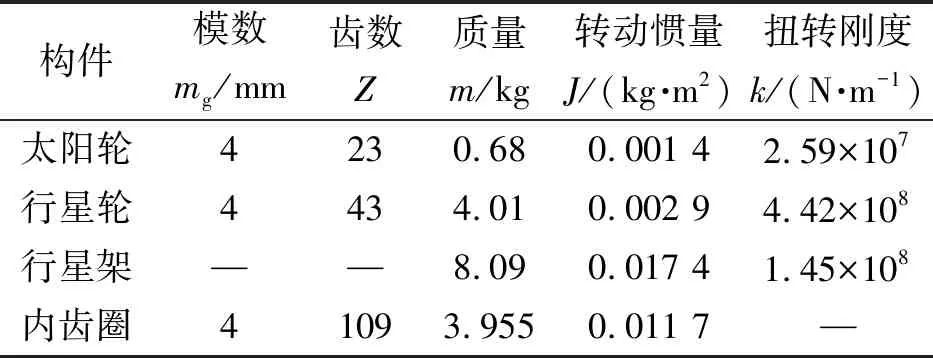
表1 人字齒行星齒輪系統主要動力學參數
2.1 阻尼變化激勵
圖3、圖4所示為外、內嚙合的動載特性隨阻尼的變化曲線。給定4種轉速考察系統的動載特性,轉速對應的量綱一嚙合頻率為1.5、1.7、1.9、2.1,阻尼比取值區間為∈[0.015,0.05]。圖3中:當為1.7時,動載系數在∈[0.021,0.023]區間內突降到1.789,然后激增到1.84;然后隨著阻尼比數值增大動載系數持續增長,在=0.038時從1.859降低到1.842左右后緩慢降低;動載系數在∈[0.021,0.023]內和=0.038時均出現短時劇烈波動,可能是外嚙合在此區域內產生非線性混沌振動,使得載荷情況突變。內嚙合(圖4)的動載系數變化趨勢與外嚙合相似但變化范圍總體降低,說明行星齒輪系統在重載工況下穩定性更好。其激增原因與外嚙合激增類似。整體上來看,隨著與增加,系統的穩定趨勢明顯。
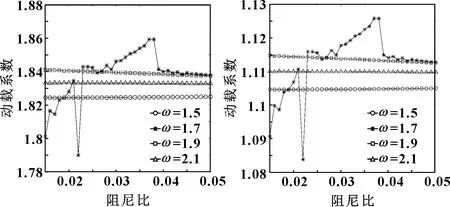
圖3 外嚙合的動載特性隨阻尼的變化 4 內嚙合的動載特性隨阻尼的變化
2.2 時變嚙合剛度激勵
圖5、圖6所示為外、內嚙合的動載特性隨時變嚙合剛度的變化曲線。選定剛度波動系數∈[0.1,0.35],量綱一嚙合頻率取1.7、1.9、2.1。圖5中,當為1.7時,在>0.17時,動載系數產生波動;在剛度波動系數=0.22時,動載系數急劇增加到1.87,發生失穩現象,使得系統嚙合傳動狀況急劇變化,然后動載系數下降至1.8左右,隨后動載系數雖有波動,但總體處于下降趨勢;當為2.1時,動載系數則在>0.2時在1.84上下發生波動。如圖6所示:內嚙合動載系數的波動相較于外嚙合動載系數的變化更加平緩。整體上看,隨著剛度波動系數的增大,系統的動載特性會逐漸失穩,但隨著齒輪轉換為純剛性件,系統的承載能力和傳動效率將得到提高。
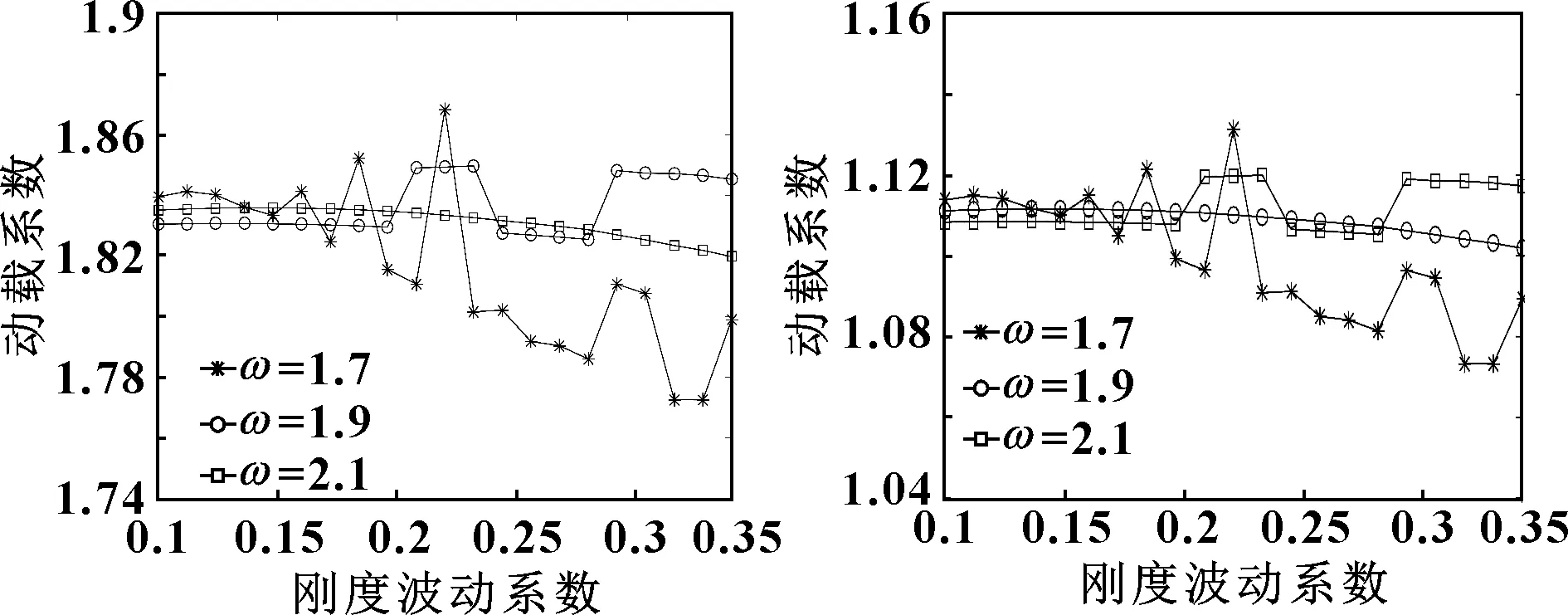
圖5 外嚙合的動載特性隨時變嚙合剛度的變化 圖6 內嚙合的動載特性隨時變嚙合剛度的變化
2.3 綜合嚙合誤差激勵
圖7、圖8分別為外、內嚙合的動載系數變化。當=1.7,綜合嚙合誤差∈[0.2,0.3]時,內、外嚙合的動載系數均出現突變,其產生劇烈波動的原因推測是在此區間中出現了微弱的齒背沖擊,使得動載波動;當>0.33時動載系數發生劇烈變化,出現了非線性混沌振動,使得系統的嚙合傳動強烈振動。在相同的系數范圍內,內嚙合的動載系數變化趨勢與外嚙合基本一致,但內嚙合動載系數變化幅度較外嚙合有所減弱,行星齒輪均載能力得到驗證。總體來看,隨著綜合嚙合誤差的增加,內、外嚙合的動載系數的變化主要呈遞增趨勢,則說明在此系統中,綜合嚙合誤差應越小越好。
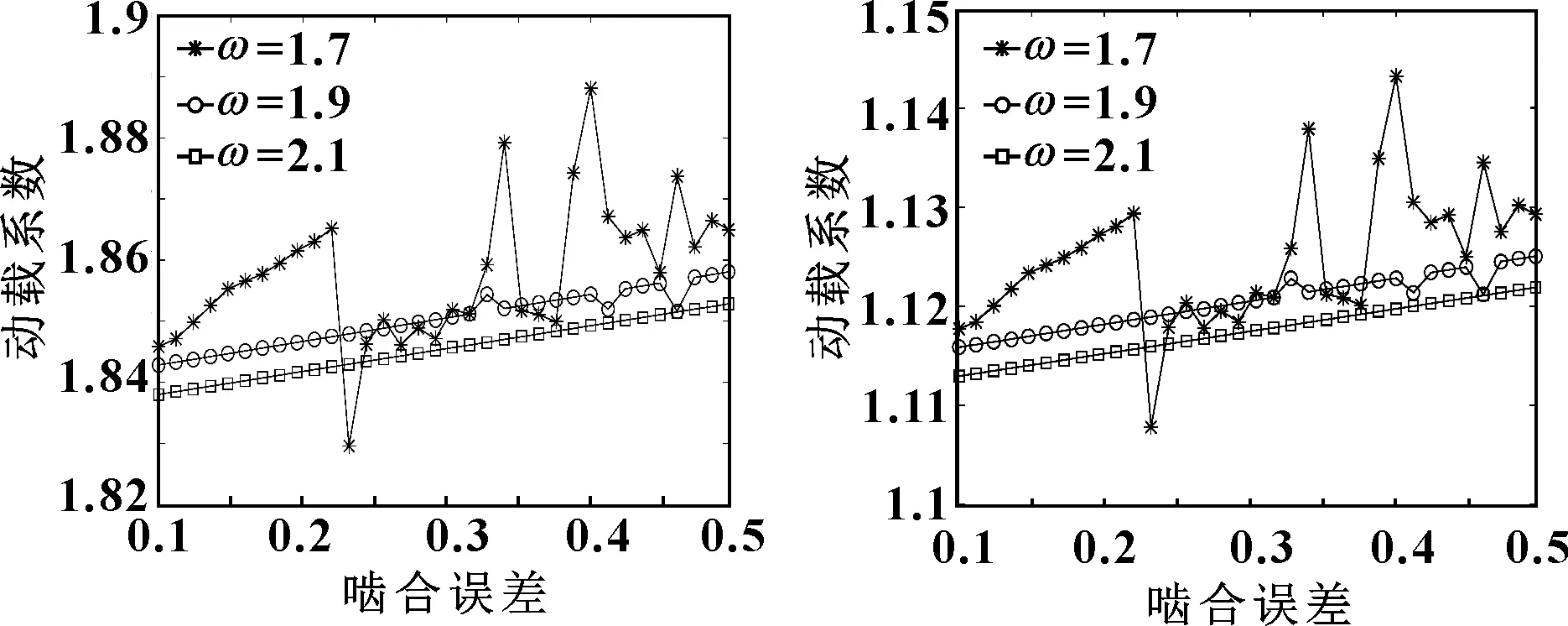
圖7 外嚙合的動載特性隨綜合嚙合誤差的變化 圖8 內嚙合的動載特性隨綜合嚙合誤差的變化
2.4 非線性特性
在上述動載性能的分析中,=0.22、=0.22、=0.4時動載系數的突變程度最大。將以上3個突出值輸入系統,然后對外嚙合不同輸入速度下的穩態響應進行傅里葉變換,獲得不同轉速下單獨的頻率內容,最后得到如圖9所示速度-頻率掃描圖的系統整體振動的三維瀑布圖。瀑布圖中每個轉速下的振動含有多個離散獨立分布的頻率。這種模擬形式可將振動情況水平分成幾個網格諧波,一次諧波比其他高次諧波更多地支配振動頻譜,特別是在運行速度較高時。此外,一次諧波和二次諧波的最高峰均對應同一頻率即1 671 Hz,該頻率為系統固有頻率的1/3,出現在激振頻率之后,系統出現超諧波共振,因此在系統運行中應注意共振情況。在兩次諧波之外,還存在一些諧、雜波,這些諧、雜波對于系統的運轉會產生一定沖擊,但是影響范圍有限。
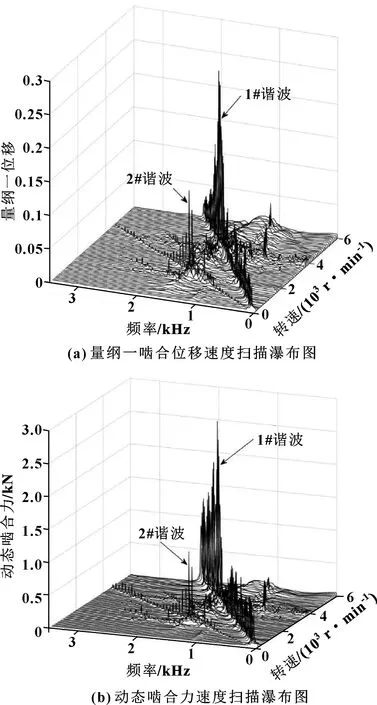
圖9 891 N·m輸入扭矩下量綱一位移和動態嚙合力響應的速度掃描瀑布圖
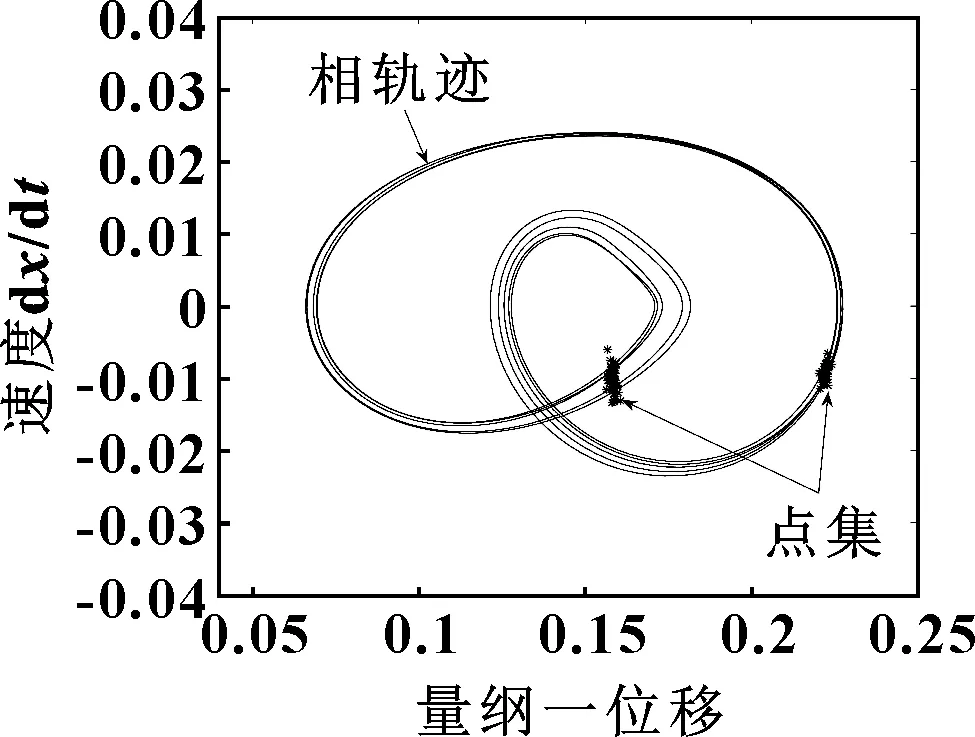
圖10 外嚙合量綱一位移-速度相圖和Poincaré映射
為進一步分析系統動態特性,將一次諧波中的最大波峰對應的太陽輪轉速5 013 r/min設定為系統輸入轉速,得到如圖10所示的外嚙合量綱一位移-速度相圖和Poincaré映射圖。圖10中相軌跡在不重合的前提下呈現交叉和纏繞現象最終形成閉環,吸引子充滿整個超環面,運動過程中并未出現明顯的齒背沖擊;吸引子點集呈現一定的擬雙周期振動特征,與圖9(a)三維瀑布圖中有2次諧波和一些諧、雜波的頻率信息相吻合,表明系統此時處于擬二倍周期運動狀態,但是存在一定的干擾。結合瀑布圖、相圖和Poincaré映射,說明系統在給定值區間仍然處于收斂狀態。
3 結論
(1)內、外嚙合的動載系數變化趨勢大致相同情況下,r-p嚙合副的波動總要低于s-p嚙合副,內嚙合具有更好的振動穩定性。
(2)阻尼比變化下的動載系數總體呈減小趨勢,但在∈[0.021,0.023]區間內動載系數發生突減現象;動載系數隨著剛度波動系數和綜合嚙合誤差數值增大而發生失穩現象,產生激烈波動,因此在系統中要避免兩者數值過大使得系統失穩。
(3)系統發生了超諧波共振,在最高振幅對應的轉速時系統處于擬二倍周期運動,系統在給定區間內收斂不發散。實際工況中應盡可能地使系統處于合適的激勵頻率區間,避開大范圍混沌運動以減輕系統的振動。

