基于改進的LMD和總變差的滾動軸承故障診斷

姜云龍 ，陳志剛,2 ，王衍學,3 ，于越 ，蔡春雨

(1.北京建筑大學機電與車輛工程學院，北京 100044；2.北京市建筑安全監測工程技術研究中心，北京 100044；3.北京建筑大學，城市軌道交通車輛服役性能保障重點實驗室，北京 100044)

0 前言

滾動軸承是工業應用機器中最重要的部件之一。如果系統中的一個軸承出現故障，將會影響機械系統的正常運行，嚴重故障的軸承還會造成十分危險的后果。因此，對滾動軸承的運行狀態進行精確的監測診斷很有必要。對滾動軸承進行故障診斷的關鍵是在振動信號中提取故障特征信息。然而，在復雜機器運轉中采集到的振動信號往往充斥著大量的噪聲信號，很難識別出故障特征。噪聲往往來自于工作環境以及一些其他耦合的機器部件，增加了微弱信號識別初始缺陷的難度。因此，如何在噪聲背景下有效增強軸承故障信息，是識別軸承故障的難點。

傳統的降噪方法是先對信號進行平滑處理，然后通過濾波降噪消除信號中的噪聲。樊高瞻等采用小波降噪技術對非平穩信號進行濾波處理，但是存在小波基和閾值的選擇問題。經驗模態分解(Empirical Mode Decomposition,EMD)是由HUANG等在1998年提出的一種自適應信號處理方法，該方法一經發表就受到了相關學者的廣泛關注。劉向鋒等針對全波形激光測高系統記錄的回波信號,采取EMD進行降噪處理，達到了去除高頻噪聲的效果。然而，EMD存在著斷點效應及模態混疊的問題。

總變差降噪方法是由RUDIN等在1992年提出的，率先應用于圖像處理中，可以在達到良好的降噪效果的同時較少地破壞原始圖像。隋文濤和張丹將總變差降噪方法應用于軸承振動一維信號的診斷，證明了其可行性。唐貴基等將總變差降噪與快速譜相結合，進行軸承故障診斷。總變差降噪在故障診斷過程中只起到去噪預處理的作用,為了能夠提取出軸承的故障特征,還需要結合較好的故障特征提取方法。

局部均值分解方法是由SMITH在2005年提出一種新型非線性非平穩信號分析方法，該方法對腦電信號分析取得了不錯的效果，但是在強噪聲背景下分解故障信號效果不佳，并且有模態混淆的現象，導致分解出虛假的PF分量。針對這一問題，董林鷺等提出一種基于局部均值分解和奇異值分解的聯合降噪法，可有效去除信號中高頻分量，進而從含噪信號中獲得有效的信號。陳長征和魏巍采用小波包降噪與改進LMD相結合的方法提取故障信息。本文作者提出一種總變差降噪(Total Variation Denoising，TVD)與局部均值分解(Local Mean Decomposition，LMD)相結合的方法TVD-LMD，對含有強噪聲的滾動軸承振動信號進行故障診斷，以達到有效降噪效果；選取真實的PF分量進行分析，完成對故障特征的成功提取，并證明該方法的可行性。

1 總變差法

總變差法是采用正則化技術進行降噪的方法，可以實現離散型信號的平滑處理。假定點信號()用向量表示為

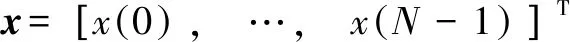
(1)

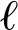
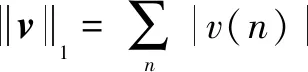
(2)

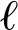
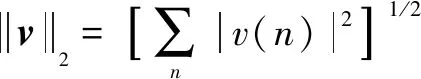
(3)

矩陣的定義為

(4)

這是點信號的一階微分定義，其中的大小為(-1)×,是如下的三角陣：

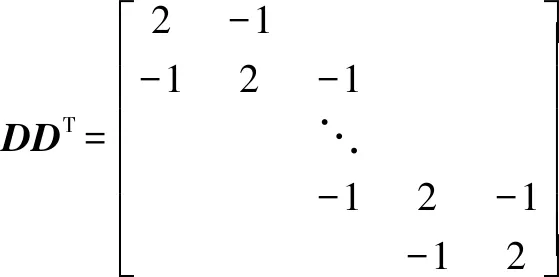
(5)

點信號()的總變差模型定義為

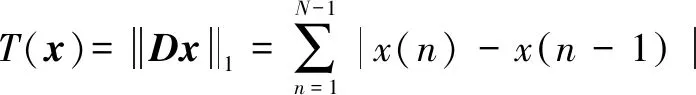
(6)

假設含有噪聲的信號()為

()=()+()=0,…,-1

(7)

其中:()為高斯白噪聲。總變差降噪可以轉化為下式的優化問題：

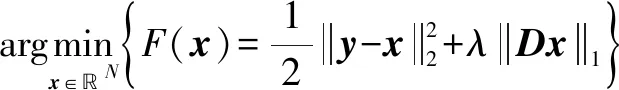
(8)

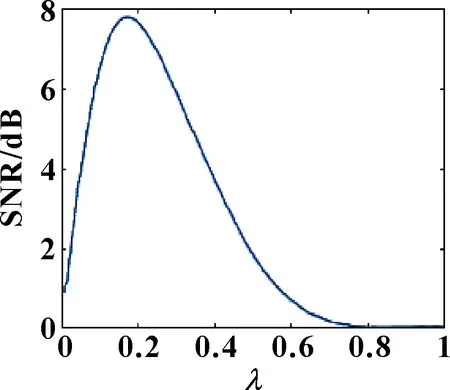
圖1 信噪比隨 λ的變化

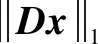
總變差降噪利用以正則化作為原始信號的先驗知識來約束重構信號的結構分布，得到信噪比較高的估計信號。選取最佳的正則化參數可以很好地剔除噪聲干擾，同時維持原始信號的邊緣特征。

2 局部均值分解

2.1 LMD原理

LMD算法是將調幅和調頻信號分解成一個PF分量，這種分離是通過平滑原始信號，從原始信號減去平滑信號，然后使用包絡估計的幅度解調結果來實現的。每一個PF分量都是包絡信號和調頻信號的乘積，從調頻信號中可以推導出時變的瞬時相位和瞬時頻率。具體的LMD分解步驟如下：

(1)確定好信號()所有的局部極值點，根據式(9)計算2個連續極值點的平均值。設定2個連續極值點分別為和+1,二者的平均值為

(9)

將局部平均值連接繪制成連續極值之間的延伸直線，使用移動平均值法對局部均值做平滑處理，得到平滑變化的連續局部均值函數()。

(2)根據式(10)計算局部均值點的包絡估計值：

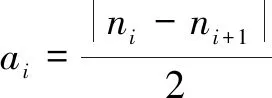
(10)

將包絡估計值以與局部均值相同的方式做平滑處理，得到平滑變化的連續包絡函數()。

(3)根據式(11)在原信號()中分離出局部均值函數()：

()=()-()

(11)

(4)根據式(12)振幅解調()得到：

()=()()

(12)

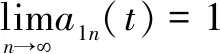
(5)把迭代過程中獲得的連續包絡估計相乘，得到相應的包絡信號：

(13)

(6)把最終的包絡信號1()與頻率調制信號1()相乘，形成第一個PF分量：

()=1()1()

(14)

(7)將原始信號減去第一個PF分量，得到一個新的信號()，將它作為一個新的原始信號重復上述過程，循環次，在()為常數或一個單調函數時結束迭代。

最終將原始信號分解成若干個PF分量和一個殘余分量()：

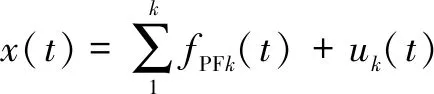
(15)

2.2 LMD的優化

為分解復雜信號進行局部均值分解時，分解得到的PF分量出現模態混疊的問題，出現虛假的PF分量，降低了故障特征提取的準確性。為剔除虛假的PF分量，將互相關系數和峭度值作為判斷指標。兩個信號的互相關系數表示的是兩個信號的關聯程度，互相關系數越大，則關聯程度就越強，一般分解出的分量信號應與原始信號的互相關系數大于0.1。峭度值是用來判斷振動信號高斯性能的指標，峭度的大小體現沖擊成分的影響程度，正常滾動軸承在運行時的峭度約為0，峭度大于0則表示滾動軸承出現故障。對微弱故障信號做故障診斷時，應選取峭度大于3的信號做特征提取，會得到較為明顯的效果。

3 實驗分析

3.1 數據采集

此次實驗用到的實驗臺是美國SpectraQuest公司生產的機械故障綜合模擬實驗平臺(MFS-Magnum)，組成如圖2所示。該實驗臺由0.75 kW(1 HP)的電機驅動，采用VQ數據采集系統(包括計算機、數據采集儀及采集卡)、壓電式加速度傳感器。此次實驗采集的滾動軸承振動數據由在軸承基座上安置的壓電式加速度傳感器測量得到。

圖2 MFS-Magnum 故障模擬實驗臺

實驗采用ER-12軸承，相關參數如表1所示。分別采集外圈故障軸承和內圈故障軸承的振動加速度數據，相關參數如表2所示。

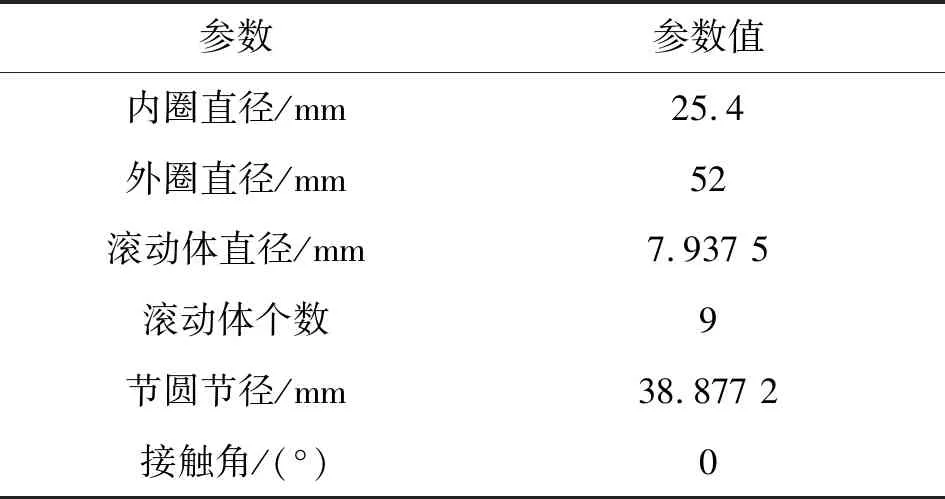
表1 滾動軸承結構參數

表2 故障實驗相關參數 單位:Hz

內圈理論故障頻率計算公式：

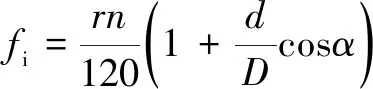
(16)

外圈理論故障頻率計算公式：

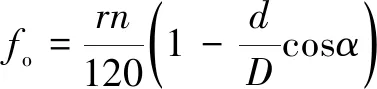
(17)

式中：表示轉速；表示滾珠個數；表示滾動體直徑；表示軸承節徑；表示滾動體接觸角。

3.2 內圈故障軸承實驗分析

由公式(16)計算出軸承內圈的理論故障頻率為161.63 Hz。內圈軸承信號的時域圖和頻域圖如圖3所示。內圈發生故障損壞時，會使主軸旋轉而帶動損傷點轉動，導致滾動體與故障點接觸的位置不斷變化，得到的內圈軸承故障信號呈現幅值調制的波形。

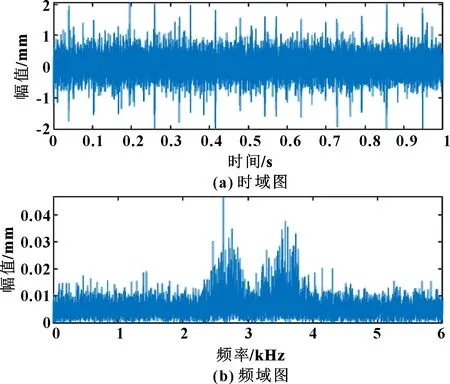
圖3 內圈故障信號的時域圖和頻域圖

由圖3可知:時域圖中存在著明顯的噪聲成分，時域圖波形復雜，降低了后續信號分析的準確度,不易分辨具體的故障位置。采用總變差降噪方法進行降噪處理，結果如圖4所示。

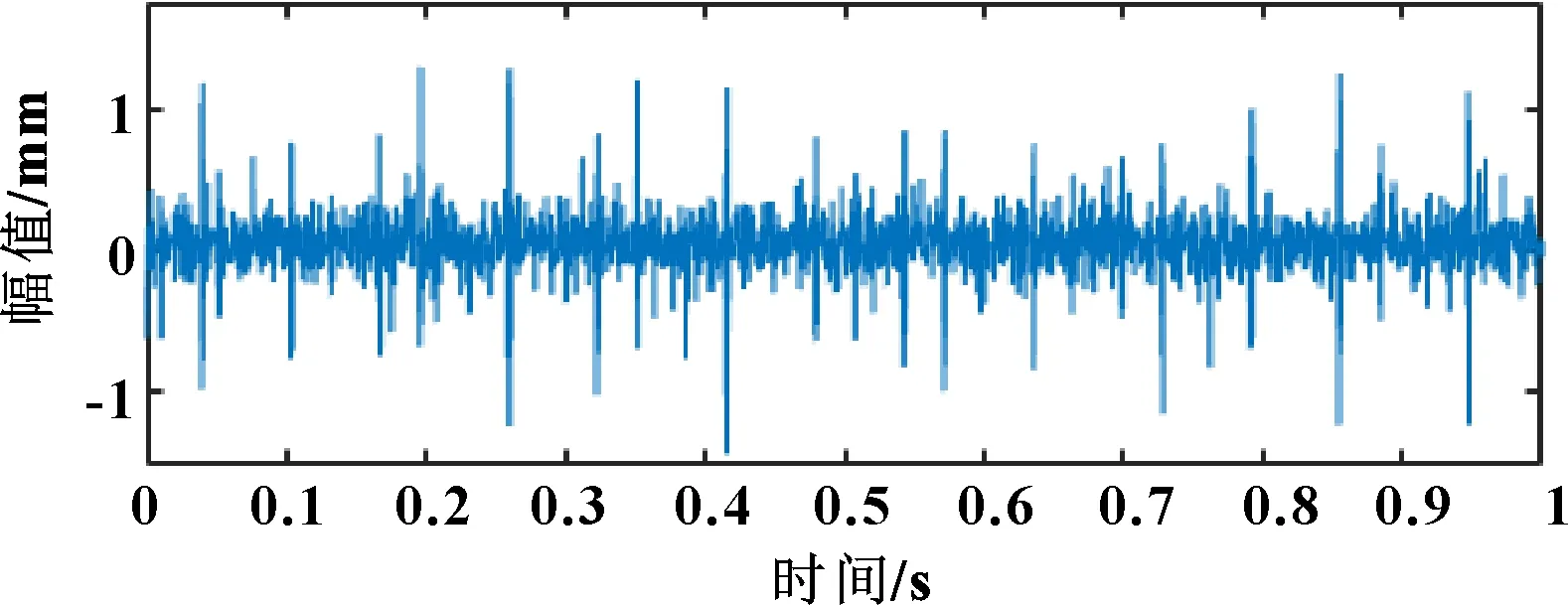
圖4 TVD降噪后的內圈時域圖

由圖4可以看出：采用總變差方法的降噪效果明顯。為對比分析降噪效果，選取小波閾值降噪的方法對該信號做降噪處理，其中db6小波降噪的結果如圖5所示。

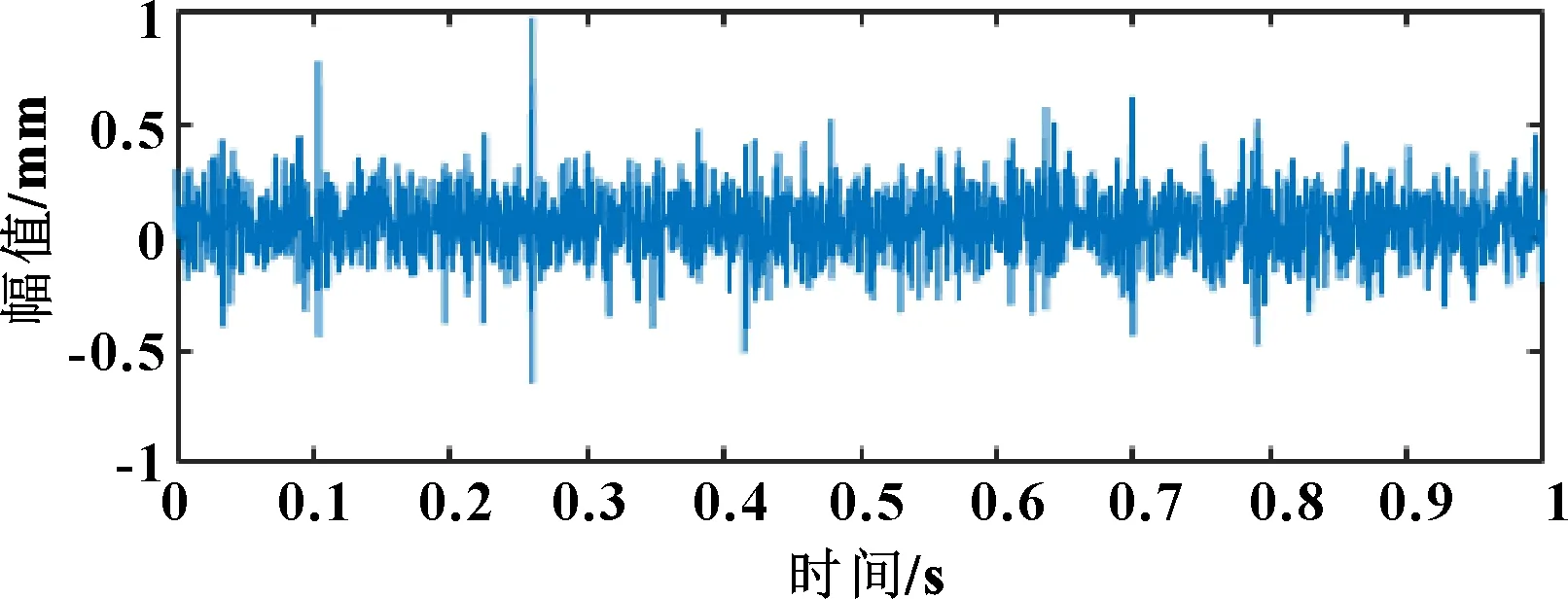
圖5 db6小波閾值降噪后的內圈時域圖

對比圖4和圖5可得：總變差降噪的效果優于db6小波閾值的降噪效果。選取信噪比和均方根誤差作為評價指標，信噪比越大，說明混在信號里的噪聲越小；均方根誤差值越小，說明各數據偏離真實值差值越小。

由表3可知:總變差降噪后的信噪比高于小波閾值降噪，同時與原信號的均方根誤差低于小波閾值降噪，進一步說明了總變差降噪具有良好的降噪效果。

表3 不同降噪方法的評價指標

進一步做LMD分解，降噪后的分解結果如圖6所示。分解后的PF分量中存在局部失真現象，需要剔除虛假的PF分量。各個PF分量的峭度和與降噪后的故障信號的互相關系數如表4所示。

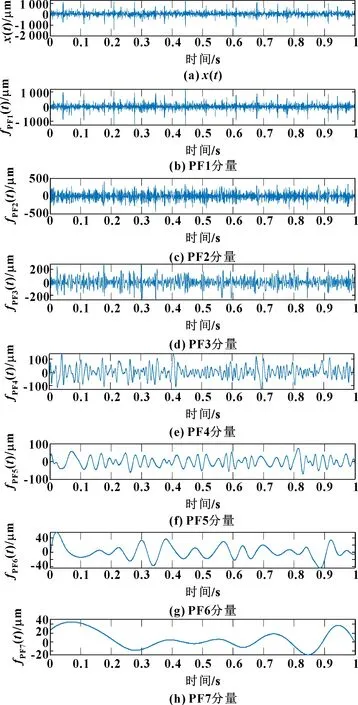
圖6 TVD降噪后內圈LMD分解

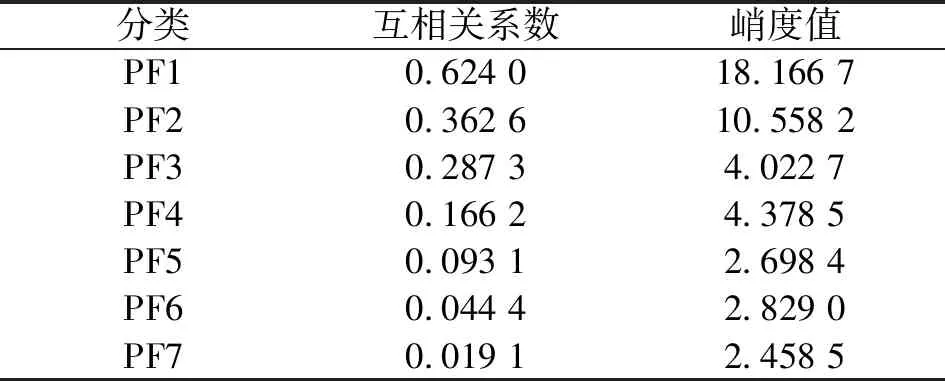
表4 內圈各PF分量的峭度值和互相關系數

從表4中可以看出：內圈故障信號分量PF1、PF2、PF3、PF4的互相關系數大于0.1，具有較強的相關性，并且峭度值都大于3，符合故障信號的特征。因此可以判斷PF1、PF2、PF3、PF4皆為真實分量。為提取更清晰的故障特征，僅選取峭度值較高的PF1和PF2進行包絡譜分析，如圖7所示。采用小波閾值降噪后進行LMD分解，結果如圖8所示。

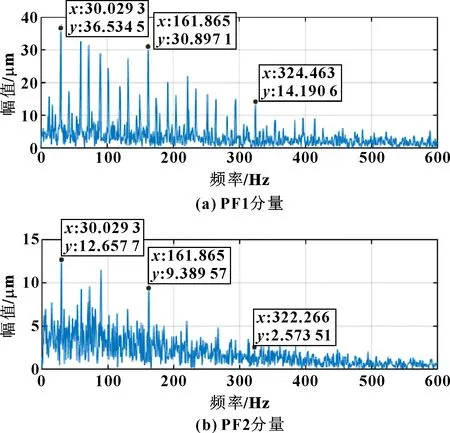
圖7 TVD降噪后的內圈PF分量包絡圖

圖8 小波閾值降噪后的內圈PF分量包絡圖

對比圖7和圖8可知：兩種方法的PF1分量，都可以在轉頻29.98 Hz、故障頻率162.49 Hz以及二倍故障頻率附近發現波峰。由于實驗測量值與真實值會有微小誤差，所以采用文中提出的方法可以判斷這個信號的內圈出現了故障。而且大于400 Hz的信號無明顯幅值，成功降低了高頻噪聲和間歇性噪聲的干擾，達到了有效的降噪效果。而圖8中PF2分量包絡圖較為復雜，無法提取到準確的故障信息；圖7中的PF2分量仍能提取到故障特征，說明總變差降噪后再進行LMD分解的效果優于小波閾值降噪后再進行LMD分解。

3.3 外圈故障軸承實驗分析

由公式(17)計算出軸承外圈的故障頻率為107.72 Hz。外圈軸承信號的時域圖和頻域圖如圖9所示。軸承外圈損傷時，軸承運行時滾動體會與損傷點撞擊產生沖擊，由于滾動體受力方向和外圈損傷點的相對位置比較固定，振動信號主要表現為周期性衰減的脈沖調制。從時域圖上可以看到存在大量噪聲的一系列沖擊信號。

圖9 外圈故障信號的時域圖和頻域圖

采用總變差降噪方法進行降噪處理，結果如圖10所示。可以看出：采用總變差法的降噪效果明顯。同樣，選取小波閾值降噪做對比分析，db6小波降噪的結果如圖11所示。

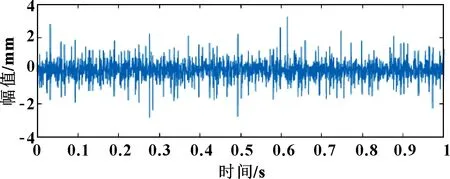
圖10 TVD降噪后的外圈時域圖

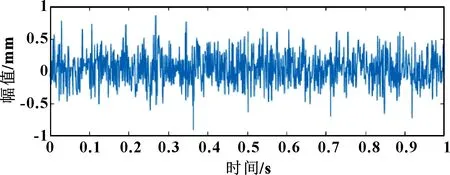
圖11 db6小波閾值降噪后的外圈時域圖

對比圖10和圖11可得：總變差降噪的效果優于db6小波閾值的降噪效果。同樣，選取信噪比和均方根誤差作為評價指標，由表5可知：總變差降噪后的信噪比高于小波閾值降噪，并且與原信號的均方根誤差低于小波閾值降噪，總變差法對外圈的降噪效果較為優異。

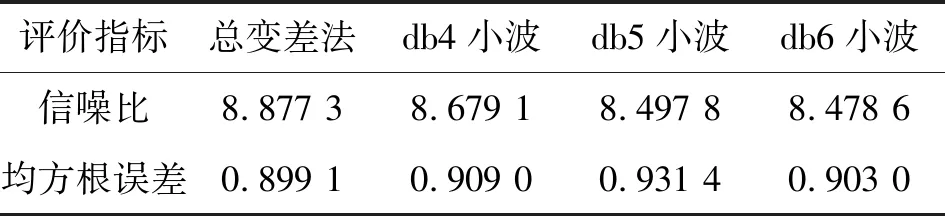
表5 不同降噪方法的評價參數

進一步做LMD分解，降噪后的分解結果如圖12所示。各PF分量的峭度值和與降噪后的故障信號的互相關系數如表6所示。

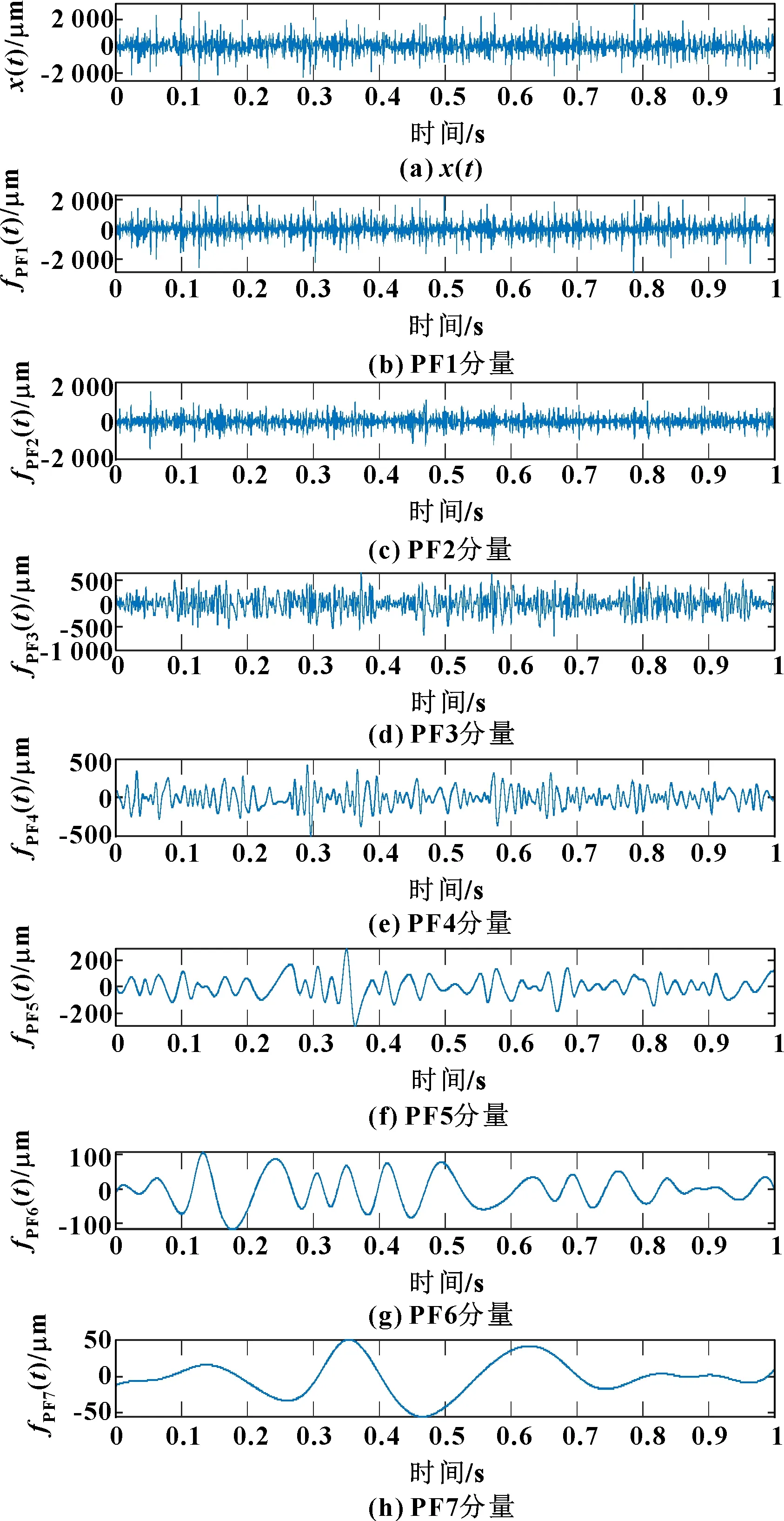
圖12 TVD降噪后外圈LMD分解

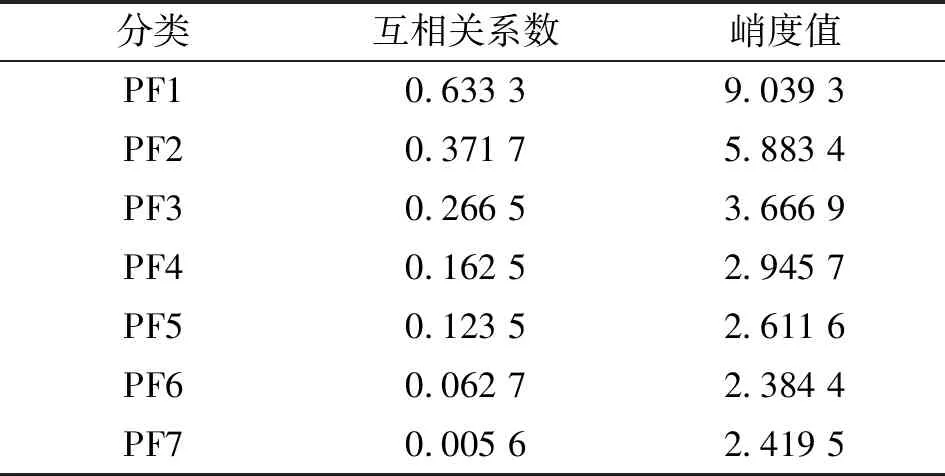
表6 外圈各PF分量的峭度值和互相關系數

由表6可以看出：外圈故障信號的PF1、PF2、PF3的互相關系數大于0.1，具有較強的相關性，并且峭度值都大于3，符合故障信號的特征，皆為真實分量。為準確提取故障特征，選取峭度值較高的PF1和PF2進行包絡譜分析，結果如圖13所示。

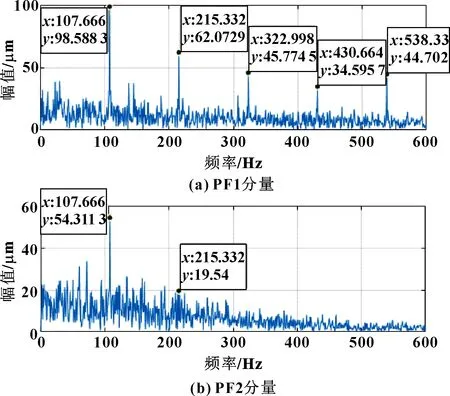
圖13 TVD降噪后的外圈PF分量包絡圖

采用小波閾值降噪后進行LMD分解的結果如圖14所示。與圖13相比，兩者的PF1分量都可以在故障頻率107.72 Hz以及2倍、3倍、4倍和5倍故障頻率附近發現明顯波峰，但TVD-LMD的波峰更加突出，提取到了更明顯的故障特征。而且小波降噪后的PF2分量過于復雜，無法提取出故障頻率。因此TVD-LMD方法可以有效降噪，實現對外圈故障的準確診斷，再一次證明了總變差法降噪后再進行LMD分解的效果優于小波閾值降噪后再進行LMD分解。

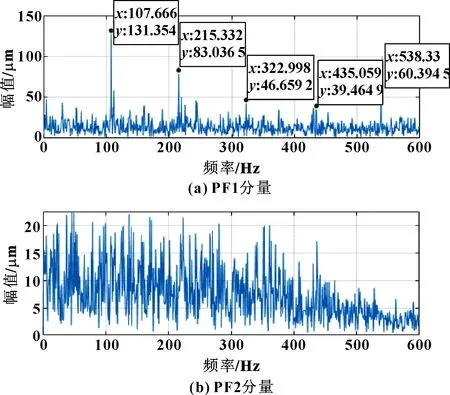
圖14 小波閾值降噪后的外圈PF分量包絡圖

4 結論

(1)在復雜工業控制系統中，滾動軸承的故障特征信號微弱，進行特征提取相對困難，采用總變差降噪對故障信號做預處理，降低高頻噪聲和間歇噪聲的干擾。分析內外圈的實測信號，結果表明總變差法的降噪效果優于小波閾值降噪，并且與LMD結合后可以達到提取故障軸承特征的目的。

(2)通過互相關系數和峭度，排除虛假的PF分量，選擇出與原始信號具有較高相關性且具有明顯沖擊的PF分量，增強了對微弱故障信號的故障特征提取，提高了故障診斷的準確性。

(3)本文作者提出的總變差降噪方法中的參數需要根據信號自身特點進行選擇。如何自適應選取最優的參數，達到更加優化的降噪效果，應進一步研究。