基于跟蹤微分器的移動機器人軌跡規劃與跟蹤控制研究

葉伯生，譚帥，黎晗，潘釗，唐永杰

(華中科技大學機械科學與工程學院，湖北武漢 430074)

0 前言

移動物流機器人(AGV)憑借快速、高效等特點正逐漸取代人工，引導傳統物流向智能物流轉變。受新冠肺炎疫情影響，少接觸和無接觸的辦公模式更是加快了AGV的部署速度。兩輪差速AGV因低成本優勢，在倉儲物流行業得到了廣泛的應用。但兩輪移動機器人非完整性和強耦合性的特點，使其運動控制難度增加，這也使得其運動規劃與控制算法成為移動機器人領域的研究熱門。在運動規劃方面，為了降低機器人的控制難度，規劃簡單的直線圓弧組合軌跡是常見的做法，但該方法存在減速轉向問題，效率較低，因此現有研究多聚焦于規劃曲線軌跡以提高機器人效率。常用的曲線包括貝塞爾曲線、正弦曲線和多項式曲線。貝塞爾曲線控制靈活，保證軌跡平滑的同時能根據環境的動態特性實時修改初始軌跡；但現有規劃方式普遍存在速度過度依賴軌跡形狀，難以參數化修改的問題。正弦曲線和多項式曲線過渡節點間處理困難，啟停過程中易發生加速度突變。在控制算法方面，常見的有模糊PID控制、Backstepping控制、自適應神經網絡控制、滑模控制、模型預測控制。模糊PID控制、Backstepping控制和自適應神經網絡控制在控制穩定后均能獲得較好的控制效果，但在實驗中常用于以勻速跟蹤圓或正弦軌跡，啟停過程存在速度突變，位姿誤差易受速度影響。滑模控制常存在抖動，采用補償方式可有效削弱抖動，但可能出現速度階躍，引入較大誤差。模型預測控制每次迭代都能獲得最優解，可以獲得較優的軌跡跟蹤性能，但運算量大且可能出現無解，因此控制系統的實時性和可靠性較難保證。

綜上，本文作者一方面利用三次貝塞爾曲線擬合光滑軌跡，并通過跟蹤微分器離散化軌跡，獲得最大速度和最大加速度約束下的平滑速度曲線，解決了移動機器人軌跡規劃和速度不連續問題；另一方面，在建立機器人位姿誤差模型的基礎上研究了機器人的Backstepping跟蹤控制方法，解決了機器人軌跡跟蹤控制問題；最后，將軌跡規劃算法與控制算法結合，通過規劃速度平滑和可參數化調整的軌跡，降低軌跡對控制器性能的影響，保證控制器平穩地跟蹤曲線，提高控制精度。

1 軌跡規劃

1.1 參考軌跡與參考速度規劃

AGV在執行貨物搬運任務前，調度系統將可用路徑點序列的坐標信息下發給控制系統，機器人根據接收到的路徑點序列進行軌跡規劃。圖1表示AGV物流機器人將貨物從點搬運到點所規劃的直線圓弧軌跡和曲線軌跡。為提升AGV貨物搬運效率，采用基于貝塞爾曲線的機器人軌跡規劃方法。階貝塞爾曲線的表達形式為

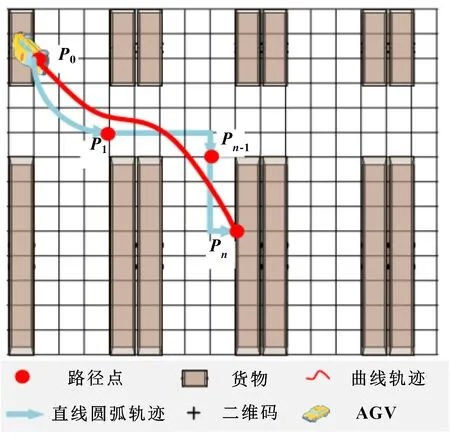
圖1 AGV貨物搬運過程

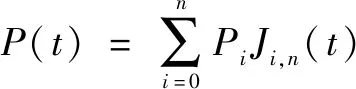
(1)

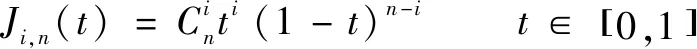
(2)

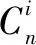
為滿足起點和終點姿態的獨立約束條件，至少需要三階貝塞爾曲線生成軌跡。更高階的貝塞爾曲線雖然提升了軌跡的平滑性與靈活性，但硬件的運算負擔也隨之加劇，不利于實時控制。綜上，以生成軌跡所需的最低階貝塞爾曲線為研究對象，采用三階貝塞爾曲線規劃機器人平面運動軌跡。由式(1)(2)得到參考軌跡的計算如下：

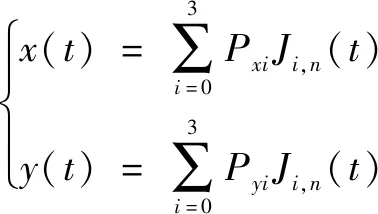
(3)

atan2(1-0,1-0)、atan2(3-2,3-2)分別表示機器人起點和終點的姿態。

求解曲線長度，以規劃機器人速度。平面中貝塞爾曲線的總長度可以運用積分方法進行計算：

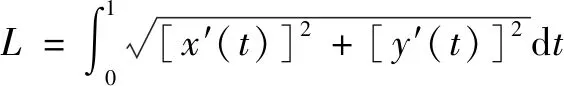
(4)

其中：′()、′()為式(3)對求導的結果。式(4)的積分表達式通常難以獲得，因此采用數值法求取曲線的長度。將貝塞爾曲線的控制參數均勻細分為份，應用Simpson公式求解曲線長度：

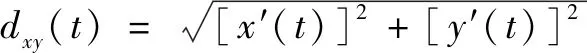
(5)

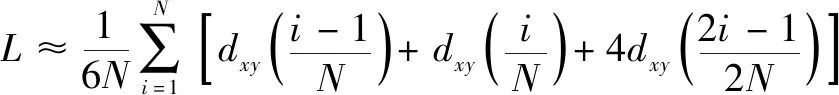
(6)

AGV的緩慢啟停和整個運行過程的速度平滑是保證貨物安全運送的關鍵，讓機器人在最大速度和最大加速度允許范圍內進行工作是機器人穩定運行的前提。針對上述要求，本文作者提出將自抗擾中獲得巨大成功的跟蹤微分器進行改造，將其運用到軌跡、速度和加速度受約束條件下的機器人軌跡規劃中。該算法有兩種實現方案：若不考慮加加速度約束，則只需改變最大速度和最大加速度兩個參數就能參數化修改機器人速度曲線，實現降速和提速，但存在速度不連續問題；若考慮加加速度約束，則不僅能實現軌跡的參數化修改，還能保證整個速度曲線的平滑連續，因此該方案是本文作者的研究重點。上述兩種方法通過跟蹤微分器對長度為的貝塞爾曲線進行速度規劃的過程分為跟蹤微分和積分兩個過程。兩種方案參考速度的計算方法如下：

算法 1：不考慮加加速度約束

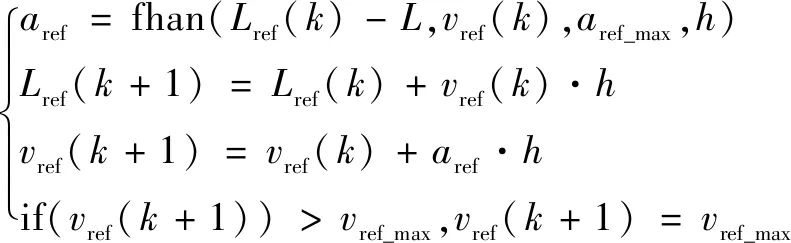
(7)

算法2：考慮加加速度約束

(8)

其中:fhan的函數表達式如下：

fhan(,,,)=

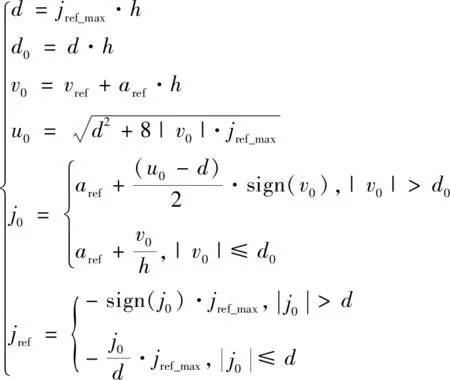
(9)

式(7)(8)為兩種算法積分過程的數學描述；式(9)為跟蹤微分過程的數學描述。其中：、、分別表示最大速度、最大加速度和最大加加速度；表示參考加加速度；代表控制周期；代表第個離散點；()、()、()分別代表·時刻所對應的軌跡長度、參考速度和參考加速度；sign為符號函數。

1.2 參考位姿與參考角速度規劃

經過第1.1節的推導已經得到了參考速度()，為了完成軌跡規劃，還需要規劃機器人參考角速度()和參考位姿(()，()，())。為此，需獲得軌跡長度()與貝塞爾曲線控制參數()的映射關系。為便于實時控制，采用Newton插值法快速獲得()對應的()，再通過()離散化軌跡，獲得對應的位姿。因軌跡長度關于控制參數單調遞增，因而對于任意()，有且僅有一個()與之對應。參考角速度與參考位姿的計算過程如下：

步驟1,由式(10)初始化參數()；

步驟2,由式(5)計算(())；

步驟3,當′()≠0時，已知曲線上任意一點對應的軌跡長度()，可由式(11)的Newton迭代公式更新參數()；

步驟4,由式(11)對()進行迭代，得到()對應的精確解()；

步驟5,將()代入式(3)中的貝塞爾曲線方程，實時更新參考位置(()，())；

步驟6,由式(12)，計算參考角度和參考角速度。

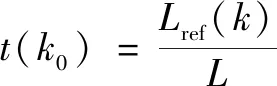
(10)

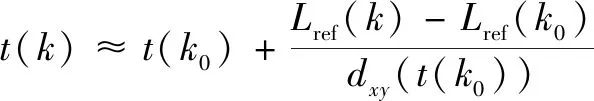
(11)

()=atan2((),())

(12)

2 機器人運動學模型

文中的研究對象由兩個萬向輪和驅動輪分別提供支撐和驅動，萬向輪對機器人運動的影響可以忽略，因此機器人的運動學模型可簡化為圖2所示的兩輪差速模型。模型中：-為參考坐標系(世界坐標系)；-為機器人坐標系；點(點)表示AGV的質心；為兩輪之間的距離，l、r分別表示機器人的左、右輪；、分別代表機器人參考速度和參考角度；、、分別表示機器人質心實際速度、角速度和角度，它們相對于參考系-描述；、表示位置誤差，表示姿態角誤差，它們都相對于坐標系-描述。

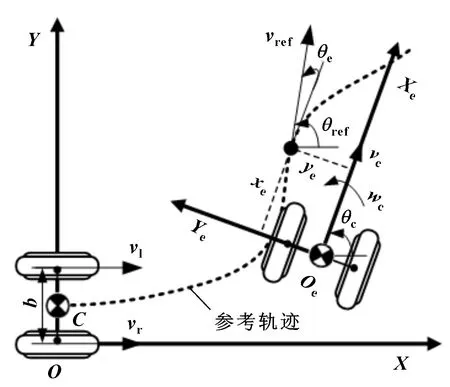
圖2 機器人簡化運動學模型

運動過程中，機器人兩輪速度和質心速度滿足如下約束關系：

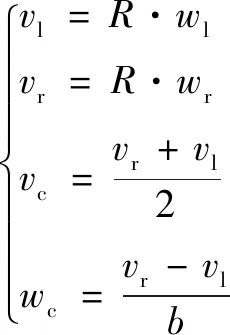
(13)

其中:為車輪半徑。由圖2中的機器人運動學模型建立誤差間的坐標變換關系，得到機器人位姿誤差方程：

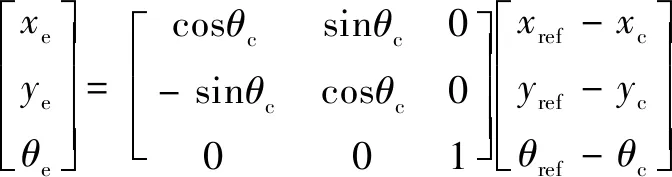
(14)

其中:、表示機器人質心位置。將上式對時間求導，并由防滑約束關系得到位姿誤差的微分形式：

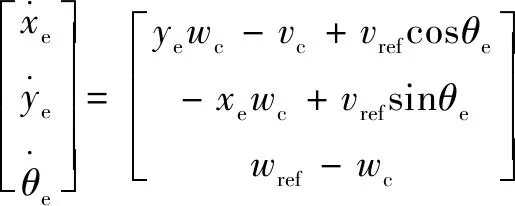
(15)

3 控制器設計

基于Backstepping方法，設計AGV軌跡跟蹤控制器：

步驟1，由位置誤差定義如下Lyapunov函數：

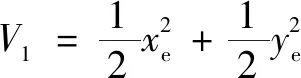
(16)

≥0，僅當、項均為0時等號成立。將各項對時間求偏導，聯立式(15)得到如下關系式：

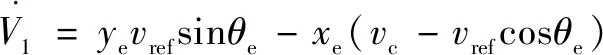
(17)

根據Lyapunov穩定性判據，為滿足項的穩定性條件，線速度的控制率取值如下：

=+cos

(18)

式中：>0。為滿足項的穩定性條件，建立變量間的虛擬約束關系，引入如下虛擬控制量：

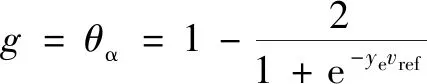
(19)

令=，考察項的穩定性變為判斷sin()≤0是否成立。求導知該不等式恒成立，且僅當=0時等號成立。聯立式(17)(18)(19)得：

(20)

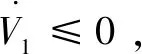
步驟2，為實現姿態角跟蹤，定義如下誤差變量：

=-

(21)

結合Backstepping思想，定義如下Lyapunov函數：

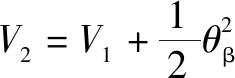
(22)

≥0，僅當、均為0時等號成立。進一步對各項進行求導，得到如下關系：

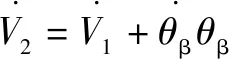
(23)

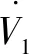
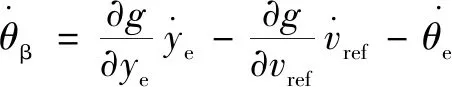
(24)

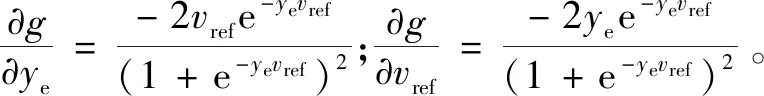
(25)

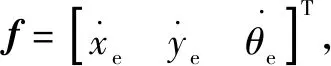
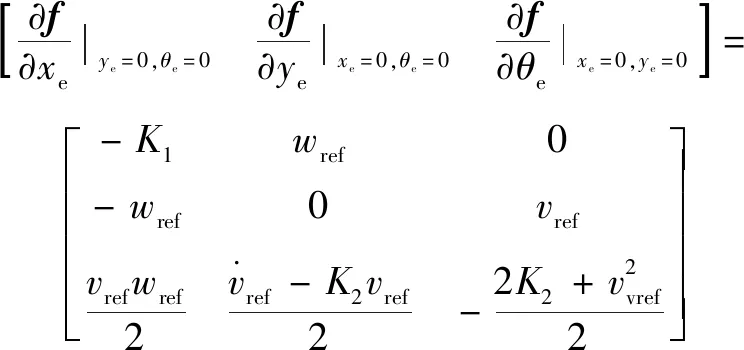
(26)

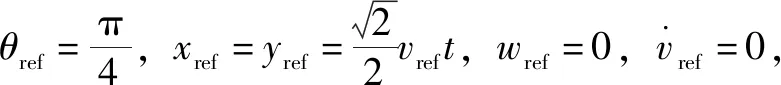
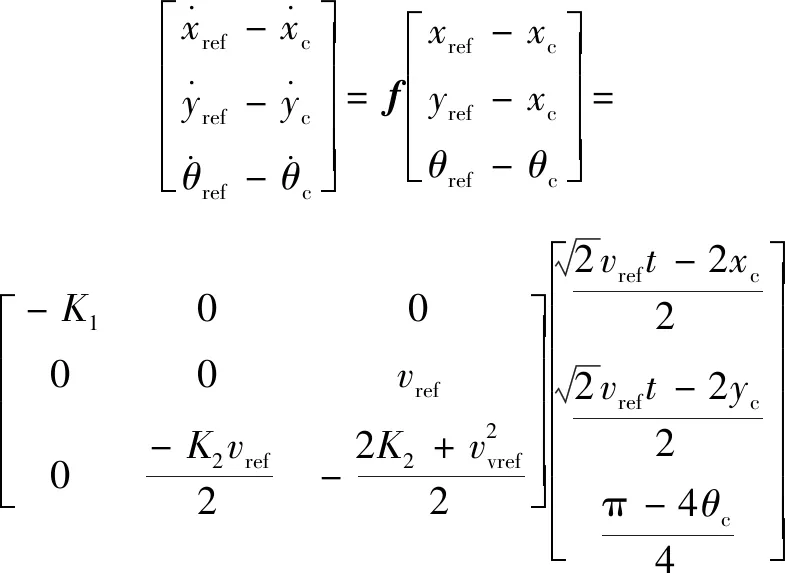
(27)

整理上面的表達式，最后得到如下關系：

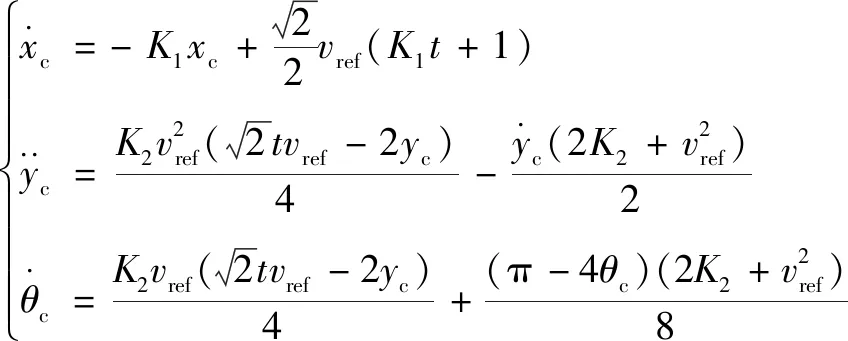
(28)

由上式知的跟蹤性能只與相關，的跟蹤性能只與相關，是個二階系統，其跟蹤性能與頻率和阻尼相關。將式(28)化簡為二階微分方程的一般形式：

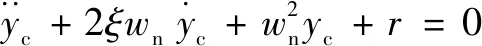
(29)

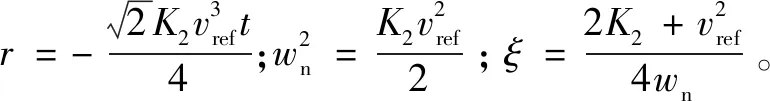
4 仿真及實驗驗證

搭建如圖3所示的AGV實物平臺和仿真平臺，驗證軌跡規劃算法和控制算法的正確性。為保證實物平臺與仿真平臺軌跡跟蹤效果的一致性，將仿真平臺中機器人的運動學和動力學參數設置成與AGV實物一致。機器人的長、寬、高分別為1 000、 750、300 mm；輪子半徑=90 mm，兩輪中心的橫向距離=711 mm。

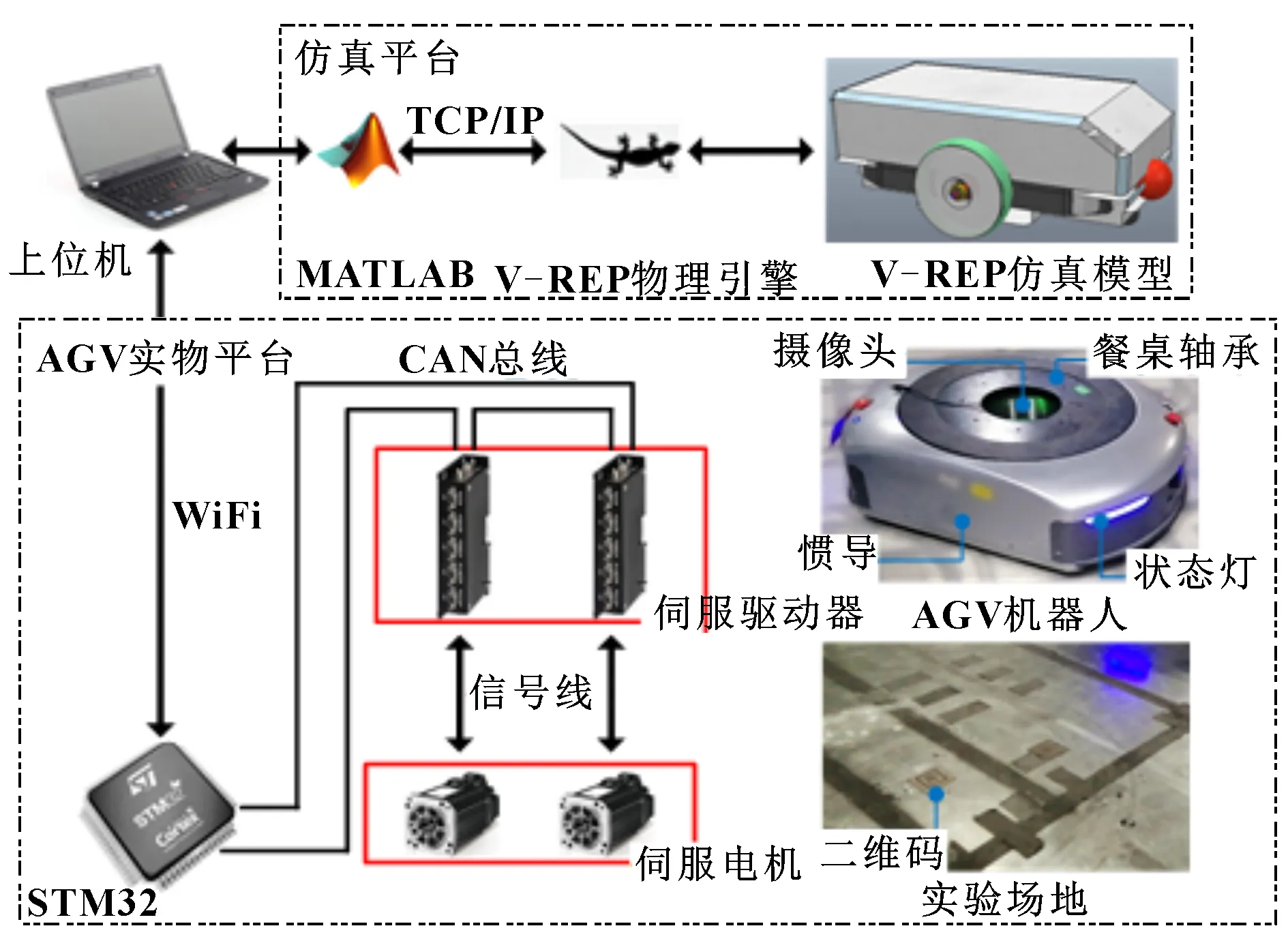
圖3 實驗平臺

4.1 仿真

4.1.1 大誤差下軌跡跟蹤仿真

為了測試算法的可靠性，實驗中人為地將機器人參考軌跡起點和實際軌跡的起點設置在相差較大的位置。仿真在V-REP軟件中進行，由Newton物理引擎計算，坐標均以mm為單位計量。仿真時用于軌跡規劃的4個控制點的坐標分別為：(0,0)、(2 100,3 200)、(4 900,800)、(7 000,4 000)。考慮不同初始狀態下，機器人軌跡收斂情況不一致，為此設計了機器人在4種不同初始狀態下的仿真實驗。4個實驗中，機器人起點分別位于世界坐標系的4個象限中，且每次相對于坐標原點的偏移量都是機器人機身的長度和寬度。4次實驗的起點坐標分別為(-750,-1 000)、(750,1 000)、(-750,1 000)、(750,-1 000)，姿態角均為0 rad。仿真時采用第1.1節中的算法2進行軌跡規劃，跟蹤微分器的相關參數分別設置為=0.05 s、=600 mm/s、=500 mm/s、=1 200 mm/s。控制器的相關參數分別取為=8.2、=0.5。實驗結果如圖4所示。

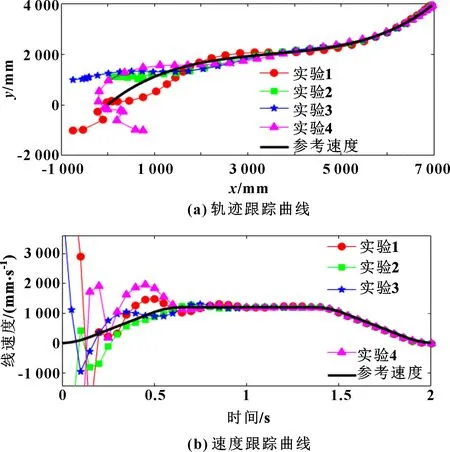
圖4 軌跡規劃及軌跡跟蹤仿真實驗效果

由圖4(a)可知：即使起點存在較大的位姿誤差，在控制作用下機器人均能逐漸向規劃的軌跡收斂，并完成軌跡跟蹤。觀察圖4(b)的參考速度可知：規劃的速度曲線能滿足速度和加速度的約束，說明了跟蹤微分器進行軌跡規劃的可行性。觀察圖4(b)中的速度跟蹤曲線可知:由于起點誤差的原因，在加速階段為了減小跟蹤誤差，機器人實時對自身速度進行調整，出現實際速度偏離規劃速度的現象；到達勻速階段后，誤差不斷減小，機器人實際速度與規劃速度逐漸貼合，并最終完成速度跟蹤。仿真結果驗證了軌跡規劃方法的可行性和控制器的可靠性。

4.1.2 小誤差下軌跡跟蹤仿真

機器人實際運行速度曲線能證明軌跡規劃的有效性，誤差曲線能反映控制器的跟蹤控制性能。為此，設計了兩組對照實驗。第一組對照實驗是機器人未規劃速度曲線與用跟蹤微分器進行速度規劃的軌跡跟蹤對比實驗；第二組對照實驗是采用滑模控制器與文中設計的控制器分別對機器人進行軌跡跟蹤控制的控制效果對比實驗。仿真實驗中，用于控制生成貝塞爾曲線的4個控制點的坐標分別為：(0,0)、(646,2 290)、(3 878,4 122)、(6 463,4 580)；跟蹤微分器與控制器的參數設置與第4.1.1節中一致；未規劃速度的軌跡跟蹤實驗中，參照文獻[17]不單獨對速度進行規劃，將機器人參考速度設置為1 200 mm/s；滑模控制器的結構形式參照文獻[12]中的VSC控制器進行設計。實驗中，機器人初始位置誤差均為0，初始姿態角誤差均在0.035 rad以內。仿真結果如圖5所示。

分析圖5中各組實驗的速度曲線和位姿誤差曲線，未進行速度規劃時，機器人在啟停階段存在速度階躍，導致產生較大的位姿誤差；采用滑模控制器進行控制時，機器人在向規劃軌跡收斂的過程中容易產生速度波動，導致出現嚴重的顫振現象；采用文中的方法進行控制時，機器人實現了以平滑連續的速度在接近零的誤差范圍內跟蹤期望軌跡。該結果表明：文中的軌跡規劃方法與控制器設計的有效性和可靠性。

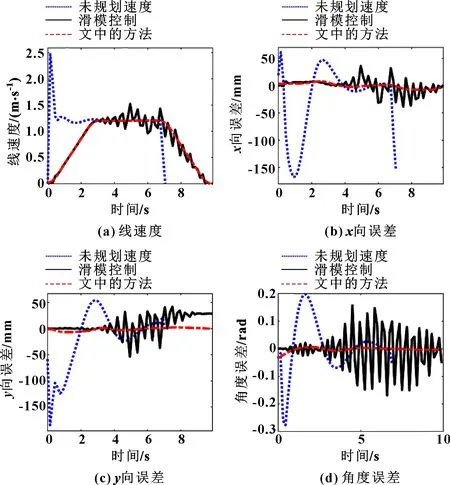
圖5 實驗對比

4.2 實驗

實驗主要是為了驗證控制器的有效性與仿真結果的正確性。實驗在由1 000 mm×1 000 mm正方形網格組成的鋁板上進行，機器人實時位姿由里程計和慣導經融合后解算獲取。實驗過程中，為了同時驗證控制器跟蹤存在速度不連續軌跡的有效性，采用不考慮加加速度約束的軌跡規劃方案，該方案規劃的軌跡在加減速階段仍存在加速度突變。實驗中貝塞爾曲線的4個控制點坐標分別為：(1 996,7 016)、(2 046,7 758)、(2 298,8 352)、(2 500,8 500)。控制器的參數與第4.1.1節中設置的一致。跟蹤微分器的參數分別設置為=0.02 s、=600 mm/s、=1 000 mm/s。實驗開始前，機器人質心在地面上的投影點位于處，車頭指向的切線方向。實驗結果如圖6所示。

觀察圖6中的位姿誤差曲線，整個軌跡跟蹤過程中方向誤差在±20 mm區間內波動，方向誤差在±10 mm區間內波動，角度誤差接近0。分析圖6中的實驗結果，整個軌跡跟蹤過程中，機器人均能穩定跟蹤規劃的軌跡，即使在存在速度突變的加減速階段，機器人仍能夠較好地跟蹤參考速度和參考軌跡，這說明了控制器的可靠性，證明了文中所設計的控制算法的有效性。

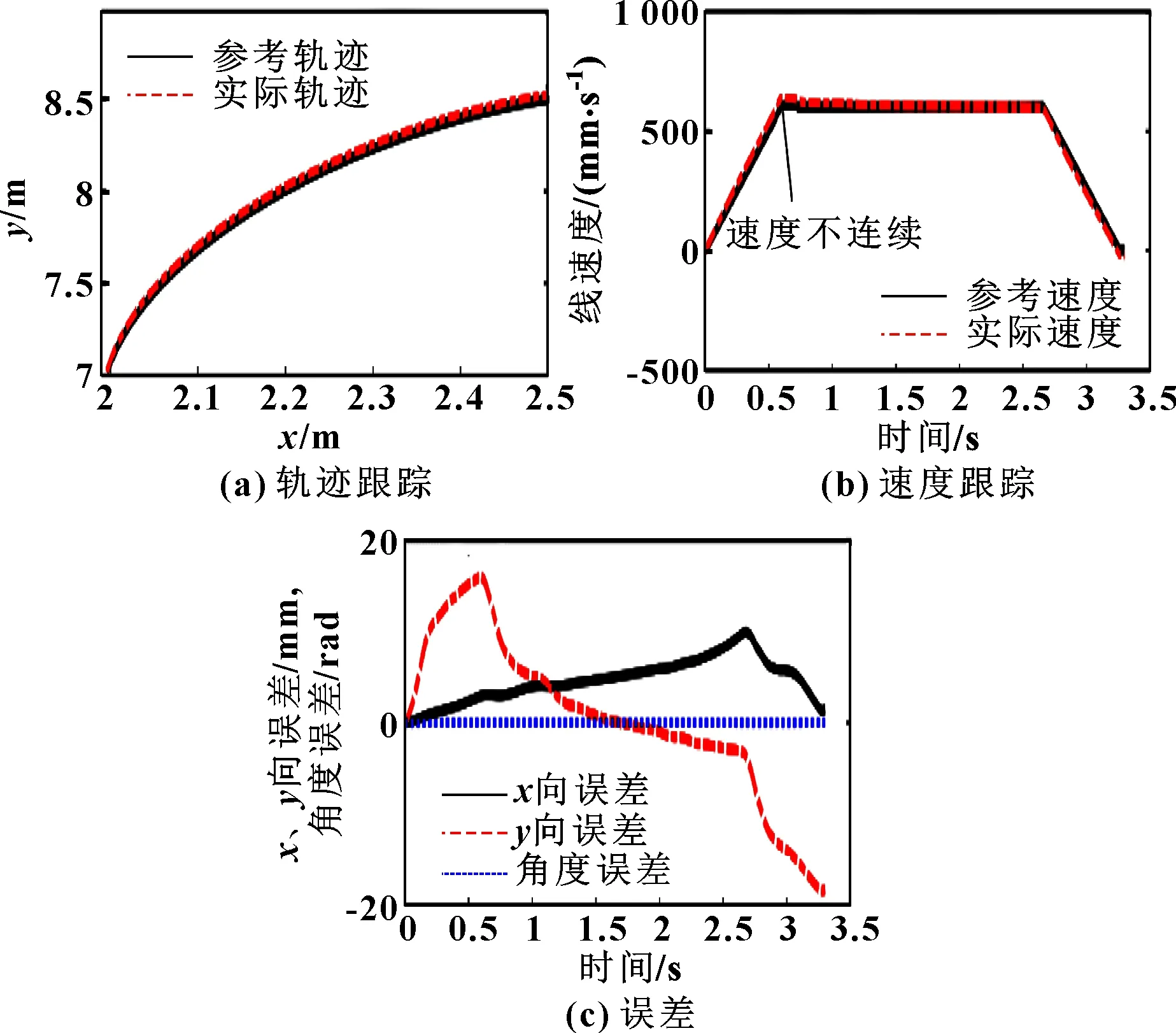
圖6 軌跡規劃及軌跡跟蹤效果

方向出現較大的誤差可能是由于速度不連續導致加速度突變，產生了打滑。實際上，在推導機器人位姿態誤差方程時，采用了防滑約束關系，因此若出現打滑將可能影響跟蹤效果。分析方向的位姿誤差曲線可知，機器人最大位置誤差實際上是出現在機器人速度不連續的階段，而這些階段恰是最容易出現打滑的階段。事實上，該實驗進一步驗證了引言中所討論的問題，即軌跡規劃不考慮速度連續問題會因為加速度突變導致跟蹤誤差倍增。

5 結論

同時研究了機器人的軌跡規劃和跟蹤控制問題。首先，提出利用貝塞爾曲線解決直線圓弧軌跡存在的劇烈轉向問題；接著，提出了保證AGV安全穩定運行的約束條件，并將約束條件作為跟蹤微分器的輸入獲得了平滑的參考速度曲線；然后，基于Backstepping方法進行了軌跡跟蹤控制器的設計，并分析了控制器參數對跟蹤性能的影響；最后，搭建了V-REP仿真實驗環境和AGV實物實驗環境對算法進行驗證。相比于未進行速度規劃、滑模控制和速度不連續等控制方式，文中提出的軌跡規劃方法與控制算法在軌跡跟蹤過程中，降低了軌跡對控制器性能的影響，提升了控制穩定性和跟蹤精度。