機器人柔性關節前饋力/位混合控制策略研究

尹曠，王紅斌，鐘連宏，張鐵，葉建斌，喇元

(1.廣東電網有限責任公司廣州供電局電力試驗研究院，南方電網中低壓電氣設備質量檢驗測試重點實驗室，廣東廣州 510410；2.華南理工大學機械與汽車工程學院，廣東廣州510641)

0 前言

在自動化生產線上，要求機器人末端執行器能夠快速定位。工業機器人中柔性部件(例如諧波減速器)廣泛存在，雖然能提高傳動效率，提供更大的傳動比，減少剛性沖擊與噪聲，但會引起關節的柔性變形，影響軌跡跟蹤精度。同時，末端執行器殘余振動現象的出現會使得機器人定位精度和速度下降，從而對機器人的可靠性和穩定度產生一定影響。

目前，對于機器人關節柔性的控制，一般可分為開環控制策略與閉環控制策略。閉環控制策略有基于奇異攝動模型的積分流形方法、PID控制、反饋線性化、自適應控制等。與開環控制策略相比，閉環控制策略對系統參數的時變特性及外界干擾表現出了更強的魯棒性，但是在實際工業應用中，采用閉環控制策略往往要求引入更多的傳感器進行測量，使得整個控制系統變得更為復雜和昂貴。因此，結合工業機器人本體反饋控制器的開環控制策略在實際應用中更加常見。其中，一種應用廣泛的開環控制策略為基于動力學模型的前饋力矩補償方法。TOMEI在傳統的PD控制器基礎上增加了基于期望參考位置的固定重力補償項。ZOLLO等通過引入“重力修正”電機位置變量，提出了添加在線重力補償項的PD控制策略。上述前饋力矩的引入，可以大幅減小PD控制器的位置增益，防止出現振蕩現象，避免驅動器飽和，而前饋力矩項的計算需要獲取系統的動力學模型，但精確的動力學模型通常難以得到。

另一種常見的前饋控制方法是輸入整形算法。在能準確獲取柔性系統參數的情況下，輸入整形器可以完全消除因關節柔性引起的殘余振動現象。但是，工業機器人所表現出的柔性系統的非線性、時變性與強耦合性，使得確定機器人柔性系統參數有一定困難。依靠不變的柔性系統參數所設計出的傳統輸入整形器已經無法有效抑制機器人在執行不同工作任務時出現的殘余振動現象。為減小確定柔性系統參數時的不確定性，常見的做法是提高輸入整形器的魯棒性，以在一定程度上降低系統參數不確定性對抑振效果的影響。然而，脈沖個數的增加會延長系統響應的時滯時間，為解決延時問題引入的負脈沖又會激發未建模模態的振動，且對于多桿機構，系統參數隨構型變化較大，單純提高輸入整形器的魯棒性也未能取得理想的抑振效果。對此，研究人員提出了自適應輸入整形器，它可以隨系統參數變化。根據是否需要對系統參數進行辨識，自適應輸入整形器可分為直接自適應輸入整形器和間接自適應輸入整形器。直接自適應輸入整形器利用機器人末端執行器附加的外設(例如加速度傳感器、壓電片)測得的殘余振動信號直接對輸入整形器參數進行調節，跳過系統參數辨識這一環節。RHIM、COLE等分別基于最優任意時滯濾波器(OATF)和有限脈沖響應濾波器(FIR)提出了直接自適應策略，降低了環境噪聲對輸入整形器參數調節的影響。間接自適應輸入整形器則需要先對系統參數進行辨識，然后根據辨識結果得到輸入整形器。設計間接自適應輸入整形器的關鍵在于實現對柔性系統參數的準確辨識，辨識方法可分為頻域辨識和時域辨識兩大類。TZES、KHORRAMI等在頻域上利用時變傳遞函數估計法(TTFE)和經驗傳遞函數估計法(ETFE)對系統固有頻率進行辨識，在線調整輸入整形器參數。該方法需要對大量的采樣樣本進行快速傅里葉變換(FFT)，計算量龐大，收斂速度較慢，因此催生了更為快速便捷的時域辨識方法。PEREIRA、TRAPERO等利用代數非漸進辨識法對單連桿柔性機械臂進行系統參數辨識，避免了初始條件不確定性問題。PARK和CHANG針對某些工業機器人重復性作業任務這一應用背景提出一種簡便的迭代學習策略，利用機器人末端附加外設采集到的殘余振動信號對輸入整形器參數進行迭代更新，最終抑制了殘余振動。

本文作者在機器人關節位置PD反饋控制律的基礎上，提出一種前饋力/位混合控制策略。該控制策略基于柔體動力學模型的前饋力矩控制算法和后置多模態自適應輸入整形算法?？紤]到多自由度機器人系統參數的時變特性，采用后置多模態自適應輸入整形器對參考軌跡進行整形，以抑制末端執行器的殘余振動。結合傳統工業機器人關節僅有電機配置編碼器的特點，建立六自由度工業機器人柔體動力學簡化模型，并將它改寫為成僅包含電機轉角變量的動力學參數辨識方程。采用加權最小二乘法對它進行參數辨識，該辨識方法不需要附加關節編碼器與其他測量設備。將動力學模型改寫為力矩計算方程，根據自適應整形后的軌跡計算得到前饋力矩并加入關節位置PD控制律中進行柔性補償，提高軌跡跟蹤精度。

1 柔體動力學建模與辨識

文中的研究對象為基于具有6個旋轉關節的六自由度工業機器人，如圖1所示。

圖1 六自由度工業機器人

引起機器人末端殘余振動的主要因素是關節柔性，故必須在動力學建模時考慮關節的柔性。本文作者采用SPONG提出的柔性關節模型，如圖2所示。該模型將柔性關節等價為彈簧質量系統，關節柔性通過線性彈簧來描述，其彈性系數即為關節剛度。與剛體動力學僅在連桿上建立坐標系不同，基于SPONG柔性關節模型建立相應的柔體動力學方程前需要在每個連桿與電機上都建立坐標系。因此，每個關節都包含電機轉角與連桿轉角2個關節變量。

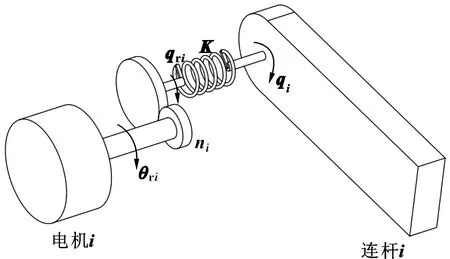
圖2 SPONG柔性關節模型[18]

利用拉格朗日能量法建立標準的柔體動力學模型：

(1)

在配置關節編碼器或采用激光跟蹤儀等外部精密測量儀器的情況下，可以同時測得電機轉角和連桿轉角兩個變量，實現對系統參數的準確辨識。但是，在工業機器人上配置關節編碼器或使用激光跟蹤儀等外部精密測量儀器會大幅增加生產成本。對此，結合工業機器人僅配置電機編碼器的特點，對標準動力學方程進行簡化，并將它改寫為僅包含電機轉角變量的動力學參數辨識方程，然后采用加權最小二乘法對它進行辨識。

利用PHAM等對柔體動力學模型的簡化方法，在進行動力學辨識時，每次使用激勵軌跡驅動一個軸運動，同時鎖住其他軸不動。將六軸工業機器人標準柔體動力學簡化為

l，2l，2=0

(2)

(3)

式中：

====0

(4)

=sin()

(5)

=cos()

(6)

=sin(+)

(7)

=cos(+)

(8)

=sin()cos(+)

(9)

=cos()cos(+)

(10)

=cos()sin(+)-

cos()sin()cos(+)

(11)

=sin()sin(+)+

cos()cos()cos(+)

(12)

式中：表示連桿的轉動慣量；m表示電機的轉動慣量;表示關節的剛度;表示連桿的轉動角度;r表示電機的轉動角度;vj表示連桿的黏性摩擦力因數;vm表示電機的黏性摩擦力因數；sm表示電機的庫侖摩擦力因數；l，1和l，2為連桿的重力項系數；表示關節的減速比。

與標準柔體動力學方程相比，在省略了科氏力和向心力項、慣性力的耦合項、連桿的庫侖摩擦力項以及第六軸的重力項后，動力學模型的復雜程度和計算量大幅下降，為消除連桿轉角這一動力學辨識過程中的不可測變量奠定了基礎。與文獻[6-7]僅對柔性關節機器人的重力項和關節剛度建模相比，文中所建立的簡化模型還考慮了連桿與電機的慣性力與摩擦力，但忽略的科氏力與向心力等動力學項可以以下一小節中提出的通過各個關節位置控制的PD反饋控制律補償。

對式(3)進行變換，可以將不可測變量(連桿轉角)用包含可測變量(電機轉角r)的表達式表示：

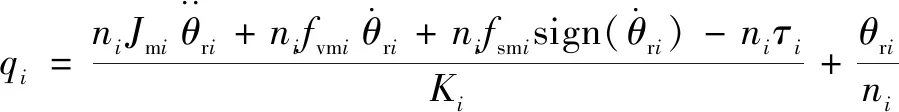
(13)

對式(13)求導可得：

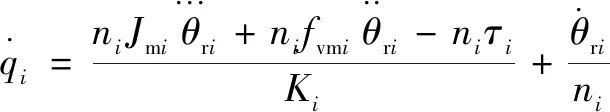
(14)

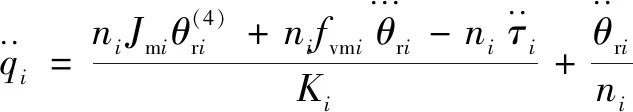
(15)

將式(13)—(15)代入式(2)，得到線性辨識方程為

=

(16)

式中：

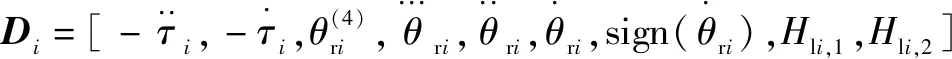
(17)

=[,,,,,,,,]

(18)

(19)

其中：為第個關節辨識方程的觀測矩陣;為第個關節待辨識動力學參數組成的向量。由簡化動力學模型所推導出的辨識方程可知，第二、三、四、五軸每個關節有9個待辨識的基礎動力學參數(,,…,)，第一、六軸因沒有重力項，每個關節有7個待辨識的基礎動力學參數(,,…,)，共計50個基礎動力學參數。

動力學參數的辨識一般是在離線條件下進行，采用事先規劃好的激勵軌跡驅動機器人，根據機器人本體配置的傳感器采回的軌跡點及對應的力矩值，利用最小二乘法可以對待辨識動力學參數向量進行估計?？紤]模型誤差及采樣時存在的噪聲問題會影響辨識結果的精度，引入誤差向量，設采集到的軌跡點樣本為個，將式(16)改寫為

=+

(20)

式中:為×1的第關節的電機實測力矩向量；為×的觀測矩陣，為關節待辨識基礎動力學參數的個數；為×1的誤差向量。激勵軌跡采用有限傅里葉級能有效提高參數辨識的收斂速度和抗噪能力。采集到的軌跡點和力矩需利用巴特沃茲濾波器和中心差分法進行數據處理，辨識算法采用加權最小二乘法以提高辨識精度。

2 基于柔體動力學模型的前饋力矩補償控制算法

第1節建立了六自由度工業機器人柔體動力學簡化模型，并給出了柔體動力學參數的辨識方法。結合已規劃好的期望運動軌跡，根據已完成辨識的柔體動力學簡化模型可以得到驅動各個關節運行期望軌跡所需的關節計算力矩。將關節計算力矩作為前饋補償控制項，與反饋力矩結合，共同作用于伺服電機底層的電流環，即將機器人控制系統分為基于動力學模型的前饋控制部分和基于伺服誤差的反饋控制部分，控制框圖如圖3所示。

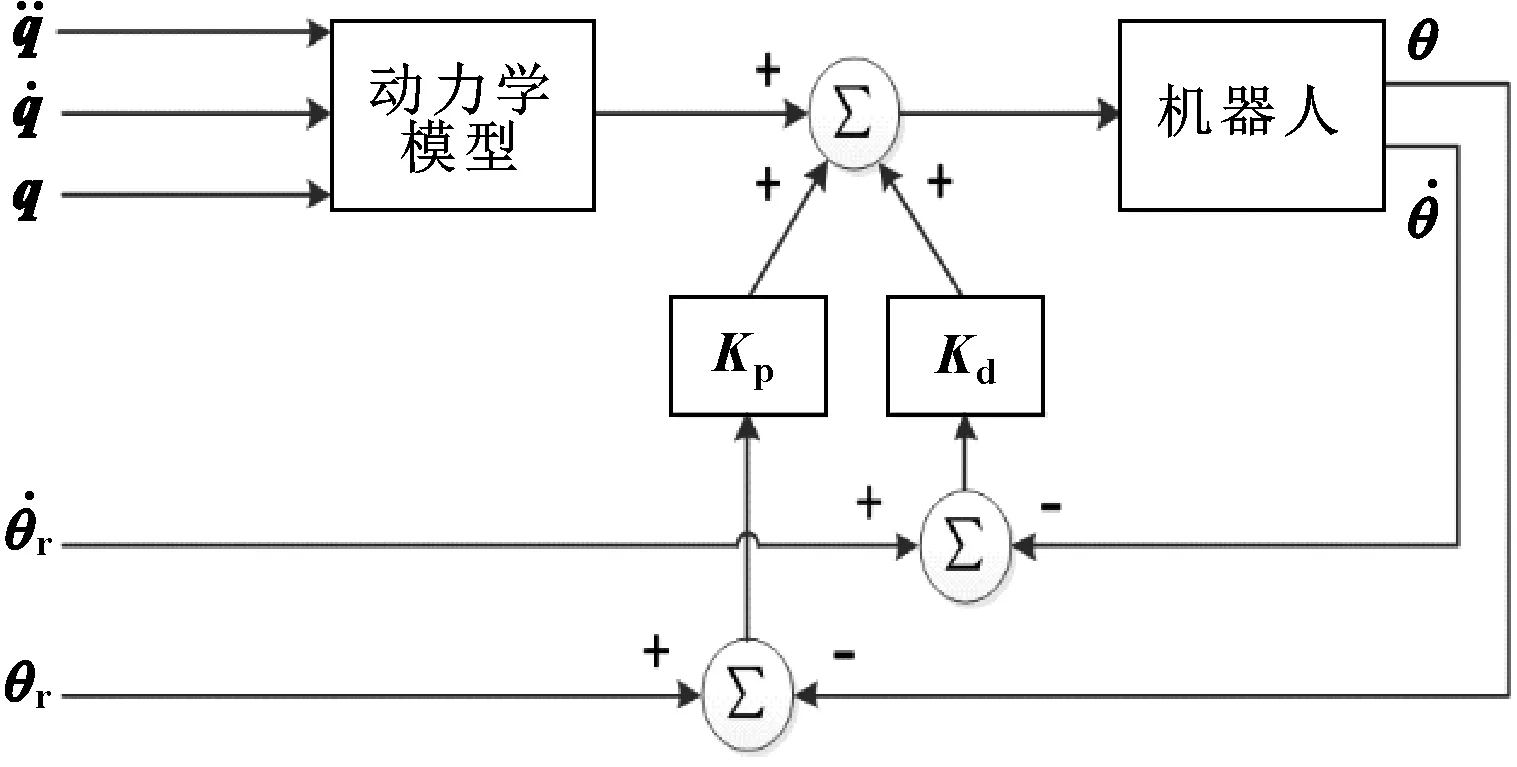
圖3 附加前饋補償控制項的控制框圖

附加前饋補償控制項的優點在于，在期望軌跡已知的情況下，可以預先通過動力學模型離線計算出機器人動力學特性中已建模部分的驅動力矩，而基于伺服誤差的反饋控制部分則僅需提供用于補償系統外部未知擾動或未建模部分等非確定因素引起的力矩。與傳統的獨立關節PD控制系統相比，附加前饋補償控制項可以減少PD反饋控制增益，避免過高反饋增益帶來的驅動器飽和問題，減少機器人軌跡跟蹤誤差。而文中所采用的基于柔體動力學簡化模型的前饋力矩補償控制方法，與文獻[6-7]中的重力項補償方法相比，前饋計算力矩不僅包括運行期望軌跡所需的重力項，還包括慣性力項、連桿與電機的摩擦力項，可以進一步減少PD反饋增益，提高機器人的動力學性能。第1節中建模時所忽略的科氏力等動力學項，可由基于伺服誤差的反饋控制環節進行補償。

一般來說，規劃好的期望軌跡僅為關于連桿轉角的函數，故需對第1節所建立的柔體動力學簡化模型進行修改，消去中間變量電機轉角。在不考慮重力項的情況下，式(2)可以寫為如下形式：

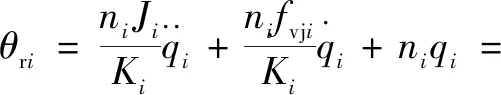
(21)

對式(21)求導可得：

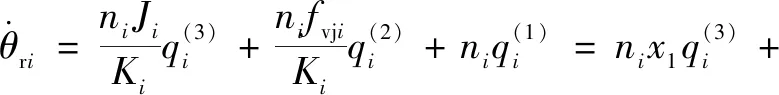
(22)

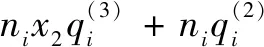
(23)

將式(21)—(23)代入式(3)，再考慮重力項的影響，可得基于柔體動力學簡化模型的前饋力矩計算公式：

(24)

式(24)僅與待辨識的動力學參數和規劃好的期望軌跡及其導數有關。機器人關節位置控制律最終可以表示為

(25)

另外，與傳統的運動學控制方法不同(直接發送給電機規劃好的連桿轉角期望軌跡)，在得到規劃好的連桿轉角期望軌跡后，利用式(21)—(23)重新計算考慮了關節柔性變形的電機轉角期望軌跡，再將它發送給各個關節的伺服電機，從而降低機器人的軌跡跟蹤誤差。而關節柔性引起的殘余振動，則在下一節中通過對規劃好的連桿轉角期望軌跡進行輸入整形來解決。

3 后置多模態直接自適應輸入整形

機器人柔性關節帶來的最明顯問題是機器人末端執行器在運動停止后的殘余振動。考慮工業機器人系統的時變性與非線性特征，采用后置多模態直接自適應輸入整形前饋位置控制算法抑制殘余振動，其控制結構框圖如圖4所示。該算法跳過了系統參數辨識環節，直接利用機器人末端采集到的殘余振動信號計算輸入整形器的參數值。輸入整形器參數的調整一般包含3個部分：脈沖個數、脈沖幅值、脈沖發生時間，每個部分的調整都是一個復雜的非線性問題。對此，RHIM等選用了最優任意時滯濾波器，其最大優點是僅需要調整脈沖幅值，而脈沖個數和脈沖發生時間均可預先確定。為引入線性算法對輸入整形器參數進行優化處理，RHIM等基于線性假定置換了參數調整環節和系統的位置，采用后置輸入整形器對系統實際輸出()進行整形，得到整形輸出()。整形輸出()與期望輸出()之間存在一預測誤差()，在將參數調整環節后置處理后可以引入遞歸最小二乘法使預測誤差()最小化，同時解出后置輸入整形器的最優參數解，最后將后置輸入整形器的最優參數解傳遞給前置輸入整形器，最終抑制殘余振動。

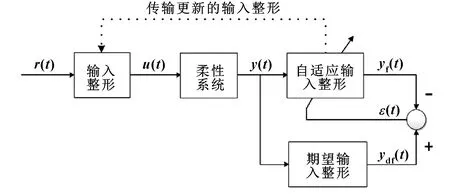
圖4 后置直接自適應輸入整形控制結構框圖

對于整形輸出()，在任一時刻有：

()=()()

(26)

式中:()=[(),(),…,()]，表示后置參數調整環節中最優任意時滯濾波器在離散時刻時的脈沖幅值，而最優任意時滯濾波器的脈沖個數與系統的振動模態階數有關。由文獻[13]可知，當脈沖個數≥2+1時，才能完全消除柔性系統的個振動模態()=[(),(-)…[-(-1)]]，表示計算整形輸出()所需要的系統實際輸出()的采樣點。

對于期望輸出()，在任一時刻有：

()=()()()

(27)

式中：()表示前置輸入整形器傳遞函數；()表示柔性系統傳遞函數;()表示參考輸出。在無法準確獲知柔性系統傳遞函數的情況下不能完全確定理論輸出()。但是由最優任意時滯濾波器的特性可知，期望輸出()在運動停止(-1)時間后必須為0。利用期望輸出()的這一部分信息，便可對預測誤差()進行最小化。文中采用遞歸最小二乘法進行求解，為保證整形前后系統輸出的穩態值不變，需對標準遞歸最小二乘法進行修改，添加歸一化條件，即：

()=1

(28)

式中:=[1,1，…,1]，添加歸一化條件約束后可得到后置輸入整形器在離散時刻時的脈沖幅值向量()表達式為

(29)

迭代初始值為

(30)

給定一個時滯時間，從初始值出發開始迭代，選取迭代的收斂值為后置輸入整形器的最優參數解，再將它傳輸給前置輸入整形器。在求解輸入整形器的最優參數解時所用的系統實際輸出()可以為任何能反映系統振動的信號，機器人末端的殘余振動加速度通過加速度傳感器采集。文中所提出的力/位前饋混合控制策略控制框圖如圖5所示。

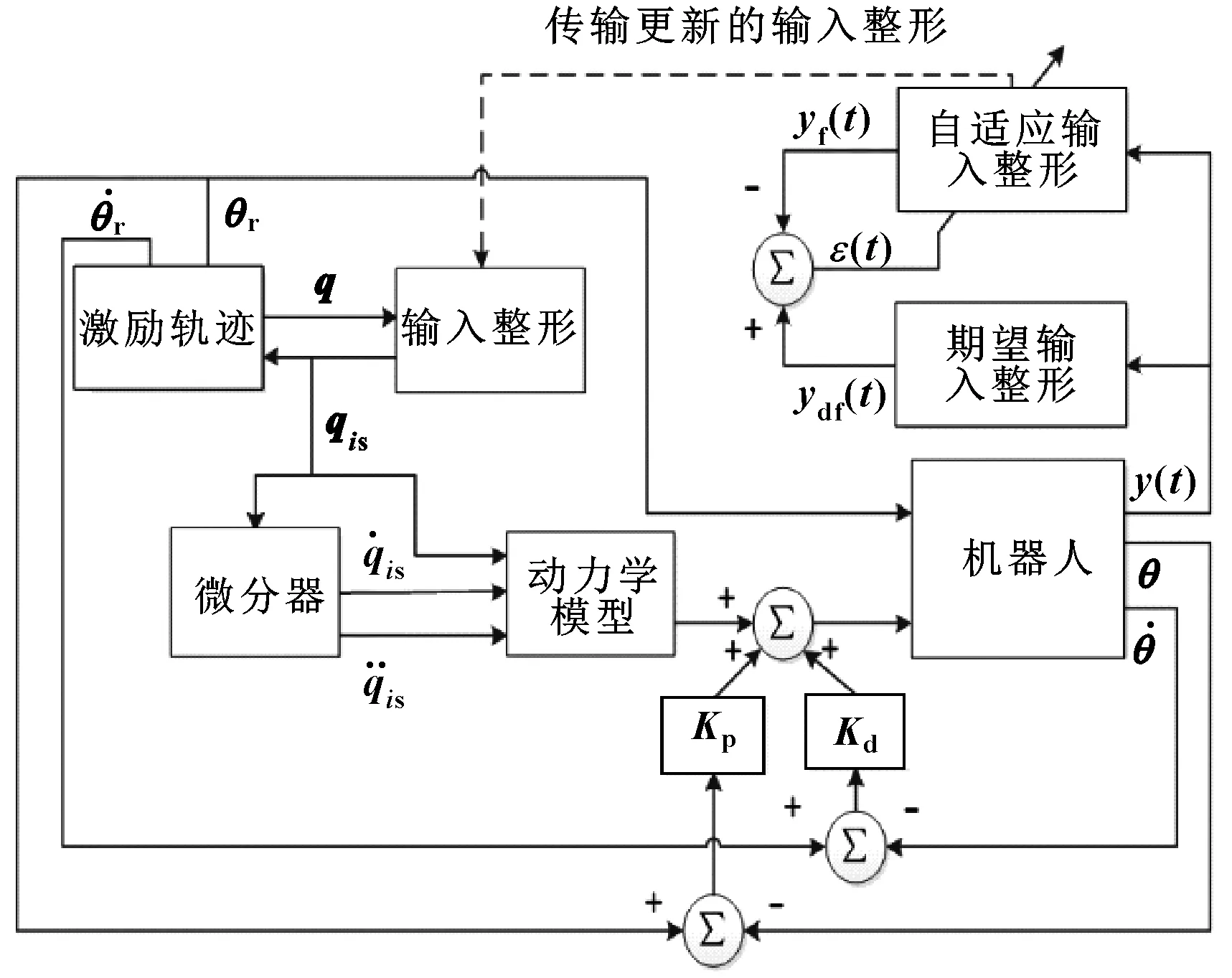
圖5 力/位混合前饋控制框圖

由軌跡發生器產生連桿轉角期望軌跡，利用式(21)計算出電機轉角期望軌跡，驅動機器人進行預實驗。采集機器人末端的殘余振動信號后利用后置多模態自適應輸入整形器進行求解，得到前置輸入整形器的最優參數解。對連桿轉角期望軌跡進行整形，得到連桿轉角期望整形軌跡。根據式(24)計算出各個關節的前饋力矩值，與電機轉角期望整形軌跡一起發送至伺服電機，對目標機器人實現力/位混合前饋控制。

4 實驗驗證及結果分析

基于廣州某公司RB03A1型六自由度工業機器人進行實驗。實驗平臺如圖6所示，機器人最大負載30 N，機器人末端殘余振動信號的檢測采用Type 8395A三向加速度傳感器。

圖6 實驗平臺

4.1 柔體動力學模型參數辨識實驗

進行柔體動力學參數辨識時，每次只給一個關節發送激勵軌跡，其余關節鎖定在原位，逐一對每個關節的動力學參數進行辨識。在采用激勵軌跡進行動力學辨識實驗獲得動力學模型后，須設計一條驗證軌跡以驗證結果的準確性。將驗證軌跡代入辨識得到的動力學模型，計算得到對應于驗證軌跡的預測力矩，再用驗證軌跡驅動機器人得到對應的實際力矩，通過觀察預測力矩與實際力矩曲線的重合度判斷動力學模型是否準確。激勵軌跡和驗證軌跡的計算公式均采用有限傅里葉級數，軌跡如圖7所示。動力學參數辨識實驗得到的關節電機編碼器值和力矩值需采用巴特沃茲濾波器進行數據處理，采用中心差分法對數據進行求導,辨識算法采用加權最小二乘法，以提高辨識精度。

圖7 激勵軌跡與驗證軌跡

各個關節柔體動力學參數辨識結果如表1所示。根據動力學模型計算出的各個關節的預測力矩和實際力矩及兩者誤差如圖8所示?？芍侯A測力矩與實際力矩基本重合。根據圖8計算各關節力矩曲線最大相對誤差如表2所示，可知最大相對誤差為第一軸的25%，其余各軸均在20%以內，說明該柔體動力學模型能準確反映機器人本體的動力學特性。

表1 柔體動力學參數辨識結果

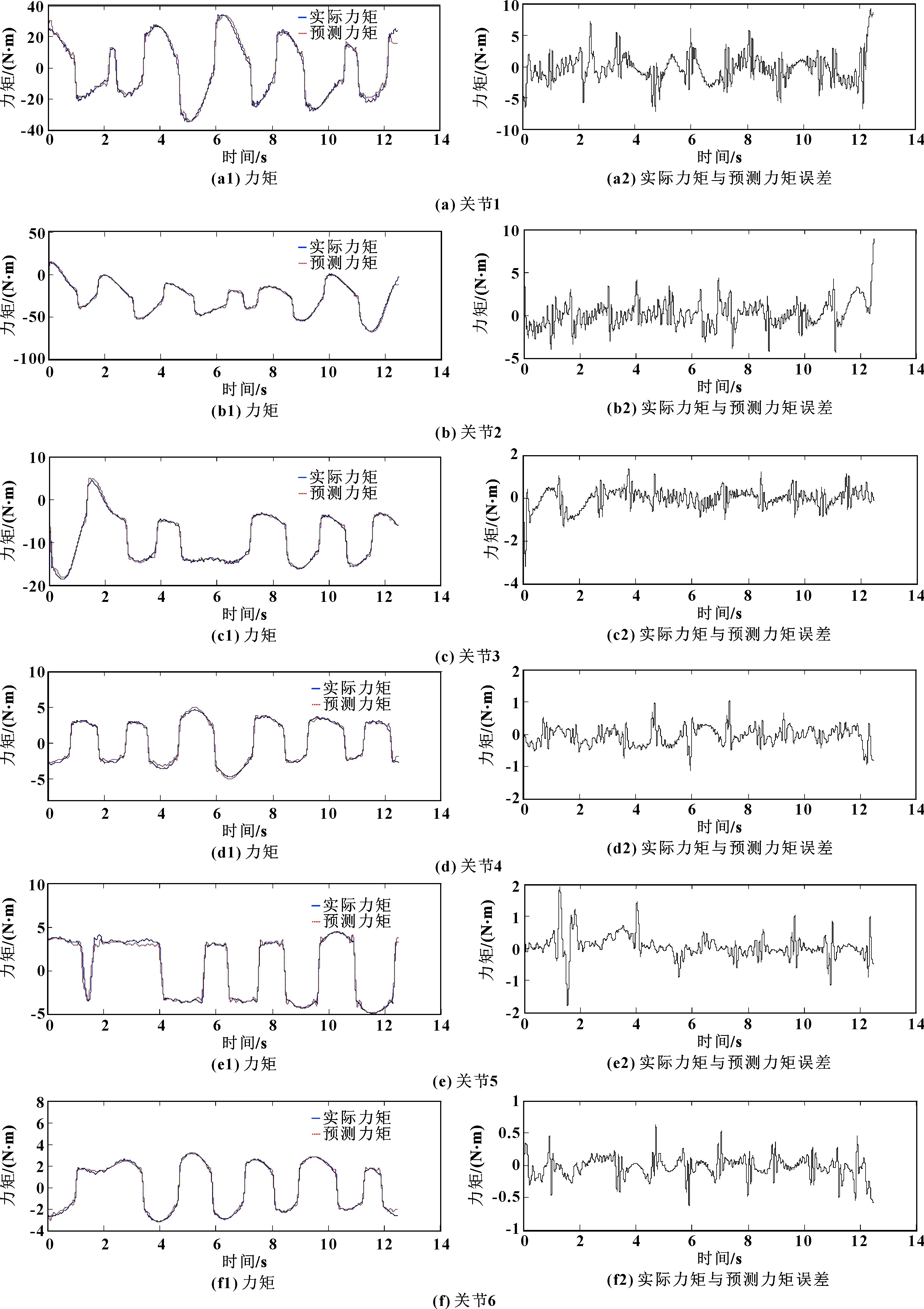
圖8 柔體動力學模型驗證效果

表2 力矩曲線最大相對誤差

4.2 前饋力位混合控制算法效果驗證實驗

文中從關節軌跡跟蹤誤差和機器人末端執行器殘余振動抑制效果兩方面檢驗所提出的前饋力/位混合控制算法實際應用效果?？紤]RB03A1工業機器人的特點，基于柔體動力學簡化模型的前饋力矩補償算法僅用于配置諧波減速器的第4、6關節，而后置多模態直接自適應輸入整形算法則用于所有關節,以保證各個關節運行軌跡時間長度相等。驗證實驗采用的連桿轉角期望軌跡為笛卡爾空間中的一條時間最優直線軌跡，因是在關節空間進行輸入整形，故需將它用逆運動學理論將笛卡爾空間直線轉換至各個軸的關節空間進行描述，如圖9所示。

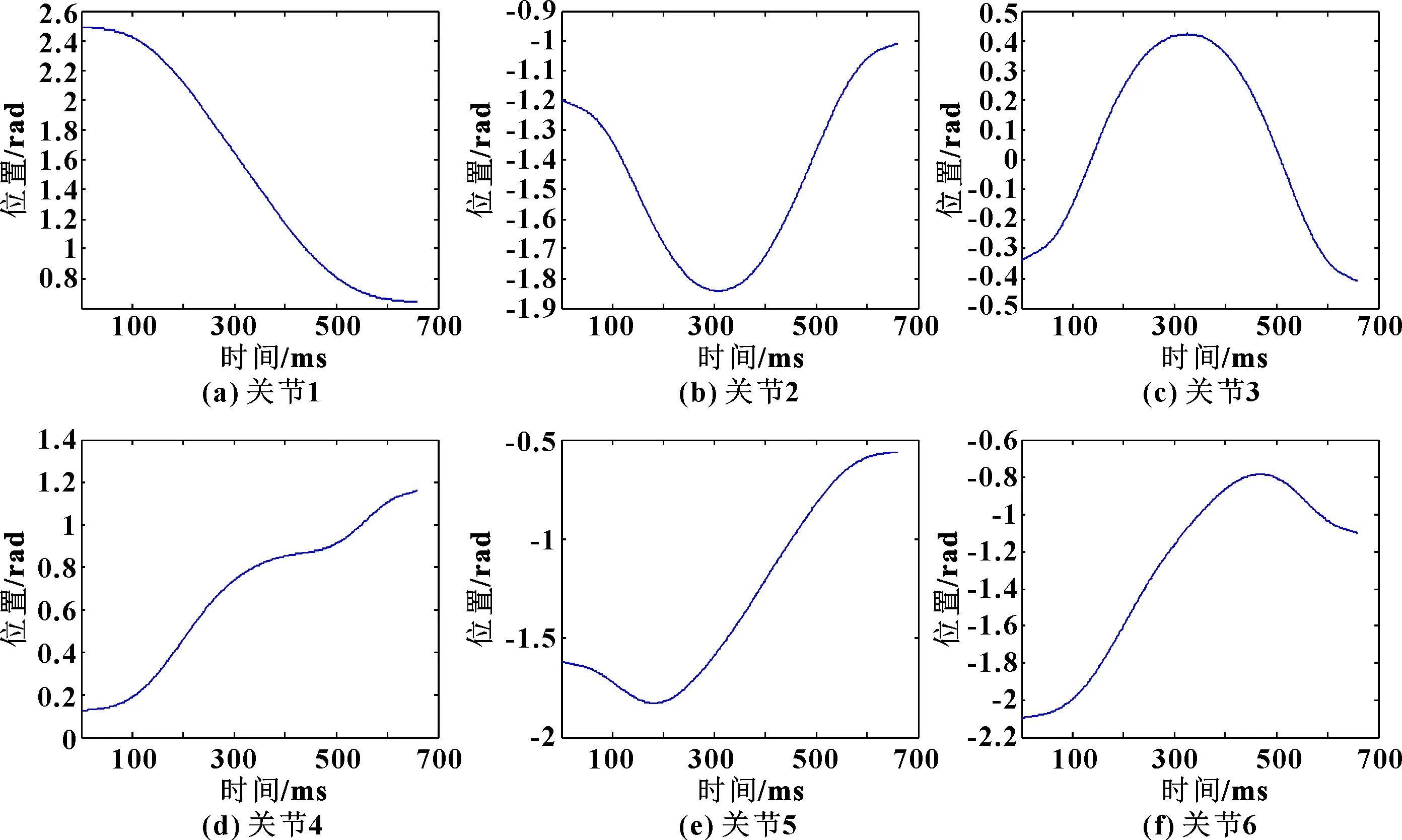
圖9 關節空間中各個關節的期望軌跡

在所提出的力/位混合前饋控制策略中，后置多模態直接自適應輸入整形器預先確定的參數分別為=5、=15 ms，根據預先規劃好的時間最優連桿轉角期望軌跡，利用式(21)計算出的電機轉角期望軌跡驅動機器人進行預實驗。采集末端執行器的殘余振動信號，選取主振方向的殘余振動加速度進行迭代計算，整形器參數計算過程如圖10所示。取最后收斂值為最優解，則整形器最后的參數如式(31)所示。

圖10 輸入整形器脈沖幅值計算過程

(31)

選用ZV輸入整形器進行對比實驗。通過后置自適應輸入整形器獲得整形期望軌跡后，代入公式(24)求解出關節4、6的前饋力矩，將它們同電機轉角期望軌跡一同發送至各個關節。為便于描述實驗結果，定義殘余振動加速度信號的最大峰值點為殘余振動最大振幅，殘余振動抑制效果如圖11所示?？芍悍较驗闅堄嗾駝又髡穹较?，力/位混合前饋控制能將、、3個方向的最大振幅減少至未整形前的10.8%、10.1%、14.5%，而ZV輸入整形器則能將、、3個方向的最大振幅分別減少至未整形前的26.6%、19.3%、45.1%。另外，考慮到環境噪聲及加速度傳感器的靈敏度問題，認為當3個方向的殘余振動加速度均衰減至1 m/s時，振動已經穩定下來。以調整時間最長方向所用時間作為該輸入整形器的調整時間，則實驗所采用的各種輸入整形器調整時間如表3所示?？芍号c未整形的軌跡相比，ZV整形器和力/位混合前饋控制算法的穩定時間分別減少至未整形前的28.7%、15.0%，表明這2種方法均能使殘余振動快速衰減。

表3 輸入整形器調整時間

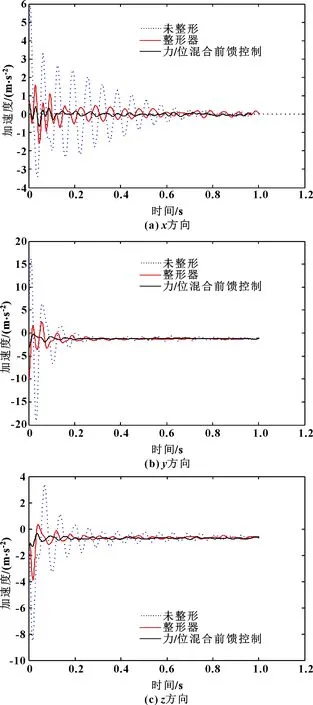
圖11 不同控制策略殘余振動抑制效果

圖12所示為關節4、6的軌跡跟蹤誤差?？芍涸谖锤郊忧梆伭匮a償控制項時，關節4僅靠關節位置PD反饋控制的軌跡跟蹤誤差均方根為0.628 6 rad，而在附加前饋力矩補償項后，軌跡跟蹤誤差均方根為0.589 3 rad，減少了6.25%；軌跡跟蹤最大誤差絕對值在附加前饋力矩補償項前后分別為1.136 1、1.039 8 rad，減少了8.47%；而對于關節6，在附加前饋力矩補償項前后，軌跡跟蹤誤差均方根分別為0.440 6、0.423 5 rad，減少了3.87%，軌跡跟蹤最大誤差絕對值分別為0.693 6、0.661 5 rad，減少了4.63%。結果表明：所提出的前饋力/位混合策略能在關節位置PD反饋控制的基礎上，有效抑制殘余振動現象，進一步提高軌跡跟蹤精度。

圖12 關節4、6的軌跡跟蹤誤差

5 結論

針對控制工業機器人柔性關節時存在的軌跡跟蹤誤差問題和殘余振動問題，進行了研究。

建立了柔體動力學簡化模型，并針對工業機器人僅配置電機編碼器的特點，將它改寫成僅包含電機轉角變量的動力學參數辨識方程，然后采用加權最小二乘法對其進行參數辨識，激勵軌跡與驗證軌跡均基于有限傅里葉級數進行構建。結果表明：利用所辨識得到的動力學模型計算出的預測力矩與實際力矩最大相對誤差為25%，該模型所反映的機器人本體動力學特性能滿足機器人動力學控制的需求。

在工業機器人獨立關節PD位置反饋控制的基礎上，提出一種基于柔體動力學簡化模型的前饋力矩補償控制算法和后置多模態直接自適應輸入整形算法的前饋力/位混合前饋控制策略。結果表明：在減少軌跡跟蹤誤差方面，所提出的力/位混合前饋控制策略能將配置諧波減速器第4、6關節軌跡跟蹤誤差均方根分別減少6.25%、3.87%，軌跡跟蹤最大誤差絕對值減少8.47%、4.63%；在抑制末端殘余振動方面，力/位混合控制策略能將、、3個方向的最大振幅減少至未整形前的10.8%、10.1%、14.5%，明顯優于傳統的輸入整形器。所提出的前饋力/位混合控制策略，可以在僅有電機配置編碼器的情況下，有效提高軌跡跟蹤精度，抑制末端執行器的殘余振動現象。