二階同步提取Chirplet變換及應用于變轉速滾動軸承故障診斷

柯偉，金仲平，呂信策，余肇鴻

(1.臺州市特種設備檢驗檢測研究院，浙江臺州 318000；2.武漢科技大學機械與自動化學院，湖北武漢 430081)

0 前言

旋轉機械被廣泛應用于眾多領域中，而滾動軸承在旋轉機械中起著至關重要的作用，同時也是最常見、最主要的故障來源之一。當軸承發生故障時，相應的故障特征會表現在振動信號中，因此對振動信號進行故障特征提取即可有效地對滾動軸承進行故障診斷。但是旋轉機械的傳動系統十分復雜，振動信號通常被淹沒于背景信號與噪聲中，難以被準確識別。并且，在實際工業生產中，設備往往是以變轉速的運行狀態工作，此時滾動軸承的故障信號為非平穩信號，傳統的故障特征提取方法無法準確識別其故障特征。因此，能夠揭示信號非線性時變特征的時頻分析方法(Time-Frequency Analysis，TFA)開始為國內外學者關注。

常見的時頻分析方法包括：短時傅里葉變換(Short-Time Fourier Transform，STFT)、Chirplet變換(Chirplet Transform，CT)、連續小波變換(Continuous Wavelet Transform，CWT)等。STFT是通過窗函數將信號切分成許多相同的小的時間間隔，近似認為每一個時間間隔內的信號是平穩信號，用傅里葉變換(Fourier Transform，FT)分析每一個時間間隔，以此來確定該時間間隔存在的頻率。但由于STFT是一種線性固定分辨率的時頻分析方法，受Heisenberg-Gabor不等式的約束，對復雜信號進行時頻分析的效果較差。連續小波變換(CWT)利用一個小波函數在局部時間窗口內與信號相乘，具有多分辨率、局部性好等優勢，但其窗口仍是相對固定的，不能夠根據信號特征調節窗口參數。CT是一種具有較高分辨率的參數化時頻分析方法，采用變換核函數，通過一個額外的調頻參數，使之能更好地匹配待分析信號，達到更優的時頻分析效果。

傳統時頻分析方法自身存在一些不足，無法滿足高分辨率的需要，這就需要對它們進行改進。為實現理想時頻表達，借鑒同步壓縮變換(Synchrosqueezing Transform，SST)算法思想，YU等提出一種新的時頻分析方法，并命名為同步提取變換(Synchroextracting Transform，SET)。與SST的壓縮方式不同，SET方法僅保留與信號瞬時頻率(Instantaneous Frequency，IF)有關的時頻信息，并去除大部分模糊能量。盡管SET可以增強能量集中度，但是由于SET依賴于恒定振幅和線性頻率調制信號的假設，在分析強調制信號時，很容易偏離真實的IF時頻脊線。ZHU等對SET算法進行了改進，借鑒CT變換的思想，提出SECT算法，并進行了驗證，得出SECT較SET確實有一定改進，但時頻面上的能量不夠集中，同時與SET一樣易受噪聲影響，計算結果的時頻面上仍具有較多噪聲成分。BAO等推導了二階SET算法，通過對STFT求二階偏導數，能夠更好地實現瞬時頻率的估計，進而使得計算結果更加接近IF曲線，但由于STFT本身受到固定窗寬的影響，其應用前景有限。

基于此，本文作者基于STFT的標準SET算法進行了理論分析；考慮到STFT受到窗寬的局限性，基于Chirplet變換推導同步提取Chirplet變換(SECT)理論，可以有效地改善時頻表達；利用相位的二階展開進行更準確瞬時頻率估計，進一步提高時頻脊線的能量集中性，提出二階同步提取Chirplet變換算法。利用模擬信號說明SECT2在應用中具有更好的時頻聚焦性。利用蝙蝠信號與變轉速試驗臺數據對所提方法進行驗證，并實現變轉速下軸承故障診斷。

1 理論描述

1.1 同步提取理論

標準SET算法基于STFT時頻譜估算瞬時頻率，設多分量AM-FM信號()的數學模型為

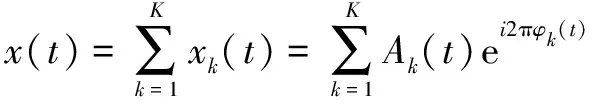
(1)

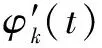
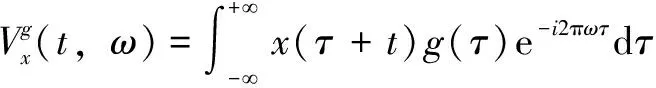
(2)

其中：()為Schwartz空間中的窗函數，定義為標準偏差的高斯窗函數：

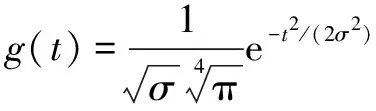
(3)

基于STFT的標準SET寫成：

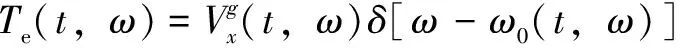
(4)

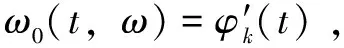
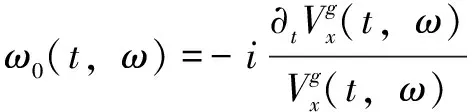
(5)

[-(,)]為同步提取算子(SEO)，滿足以下條件：

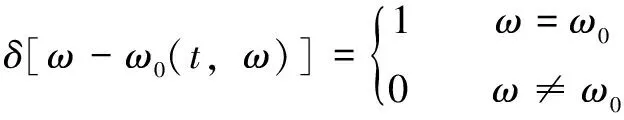
(6)

基于STFT的SET算法框架如圖1所示。由于STFT受到Heisenberg-Gabor不等式的約束，導致它進行瞬時頻率估算的結果不準確。因此,本文作者對基于CT時頻譜的IF估算展開研究。

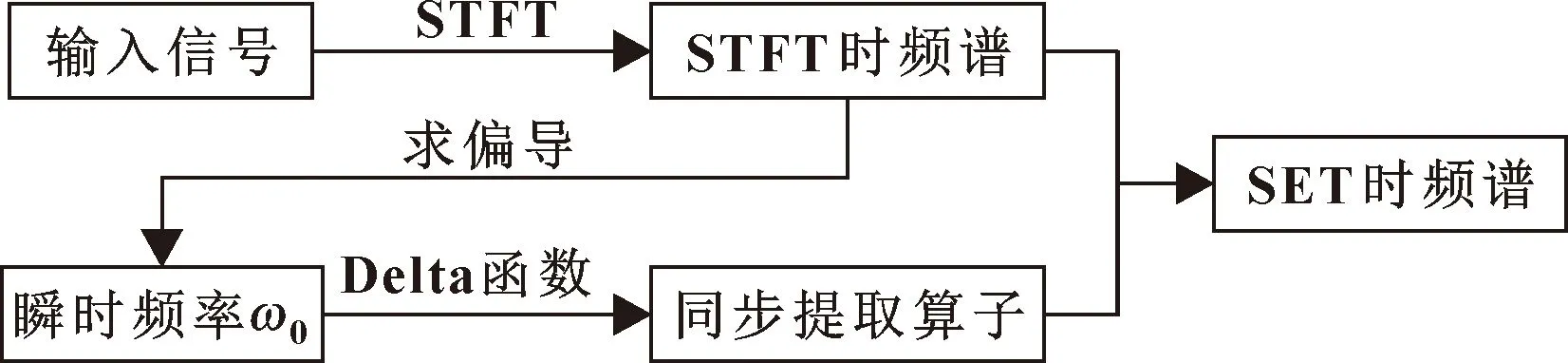
圖1 標準SET算法框架

1.2 同步提取Chirplet變換

由于STFT窗函數選定之后，分辨率無法改變，CT通過使用額外的參數調頻率(Chirp Rate，CR)進行窗口調節。對于信號()，其CT定義為

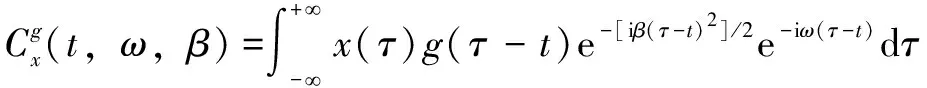
(7)

其中:為CR參數。假設在=附近，信號()的相位近似等于其二階局部展開：

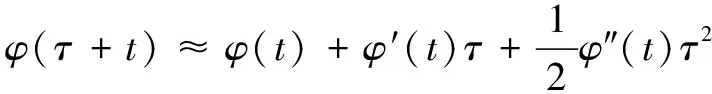
(8)

同樣，考慮幅值調制定律在=附近的展開，即：

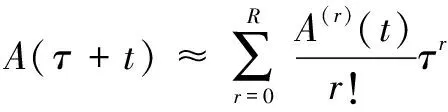
(9)

其中:為一個正整數;()為()的階導數。

基于式(8)(9)的假設，若≡″()，式(7)可以改寫為

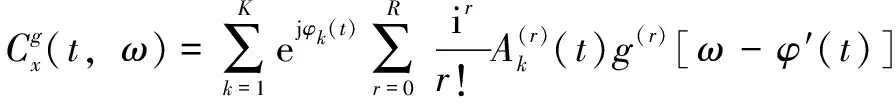
(10)

則基于CT進行的瞬時頻率IF估計公式寫為

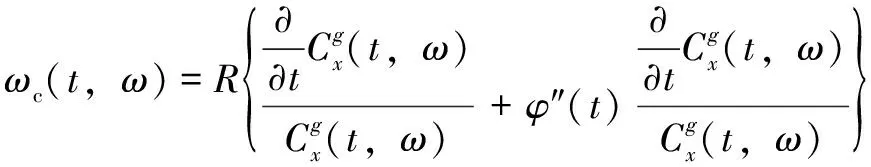
(11)

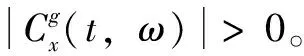
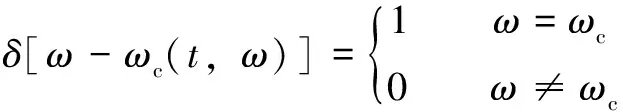
(12)

因此，SECT算法定義為

(13)

1.3 二階同步提取Chirplet變換

基于CT，式(1)定義信號()的理想時頻表示(ITFR)描述為

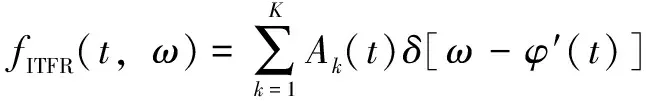
(14)

通常，假設單分量信號在每個瞬間都被高斯調制：

()=e[(-)](2)ei2π(++12)

(15)

基于此假設，信號()對的導數可以寫成：

(+)()

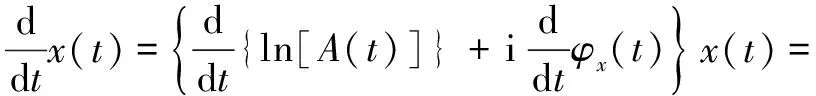
(16)

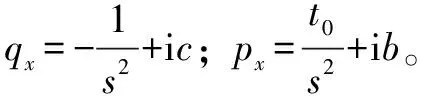
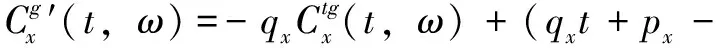
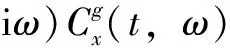
(17)

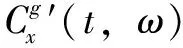
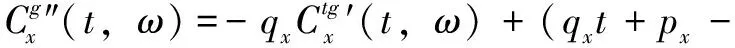
(18)

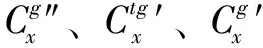
結合式(17)和式(18)，得到：

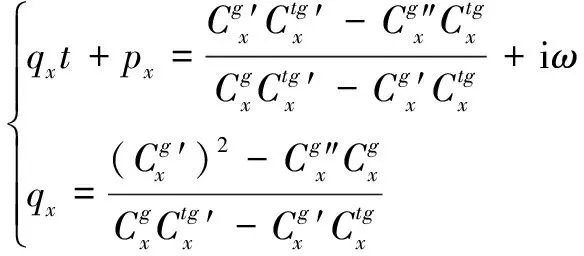
(19)

因此，對瞬時頻率IF即′()的二階估計可描述為

′(,)=(+)

(20)

其中:()表示復數的虛部。

最終，文中所提出的二階同步提取Chirplet變換(SECT2)定義為

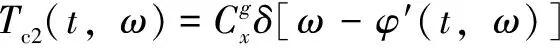
(21)

其中：[-′(,)]為二階同步提取算子。文中所提出方法的整體流程如圖2所示。

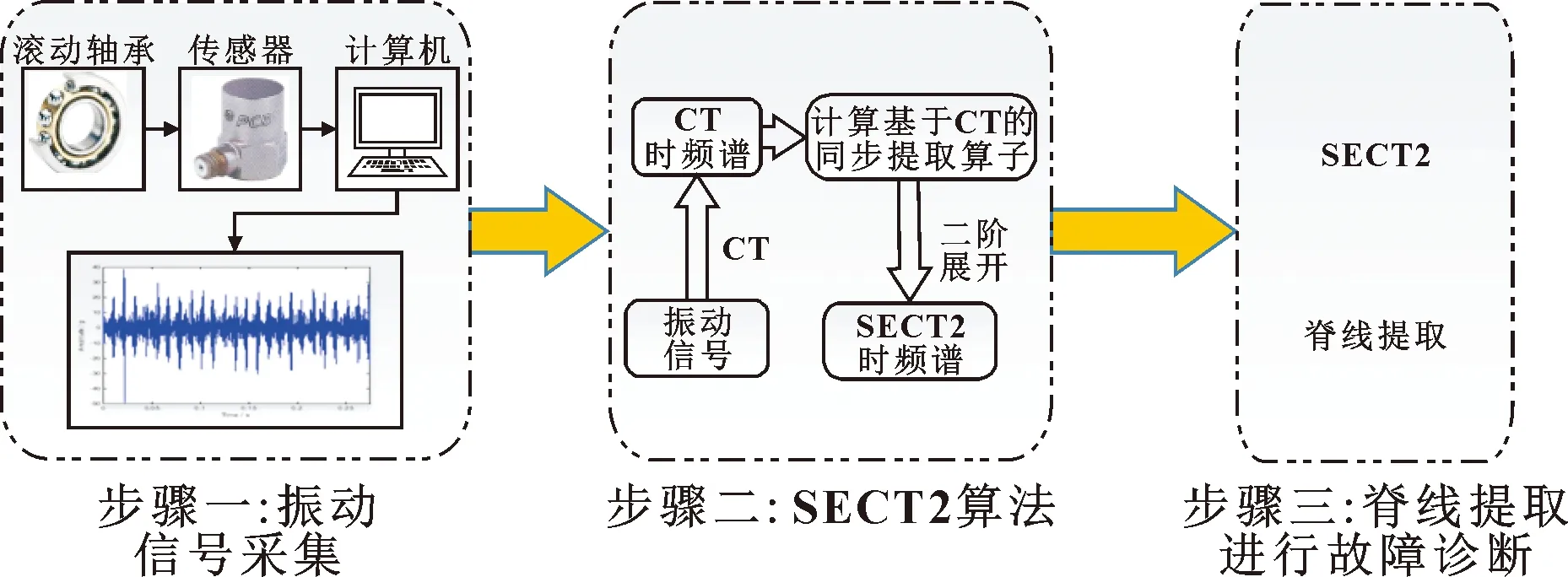
圖2 文中方法的流程

2 數值仿真信號分析

在噪聲背景下，時頻分析方法可以有效識別時變特征，正確提取不同組分的時頻脊線，即表明它具有良好的適用性。文中數值模擬仿真各組分信號設置如下：

()=e-003cos[2π(007-08+4+25)]

(22)

()=e-003cos[2π(014-16+8+50)]

(23)

()=e-003cos[2π(021-24+12+75)]

(24)

()=()+()+()+()

(25)

對模擬信號添加信噪比為15 dB的噪聲()，信號時域圖如圖3(a)所示，模擬信號的理想IF曲線如圖3(b)所示。

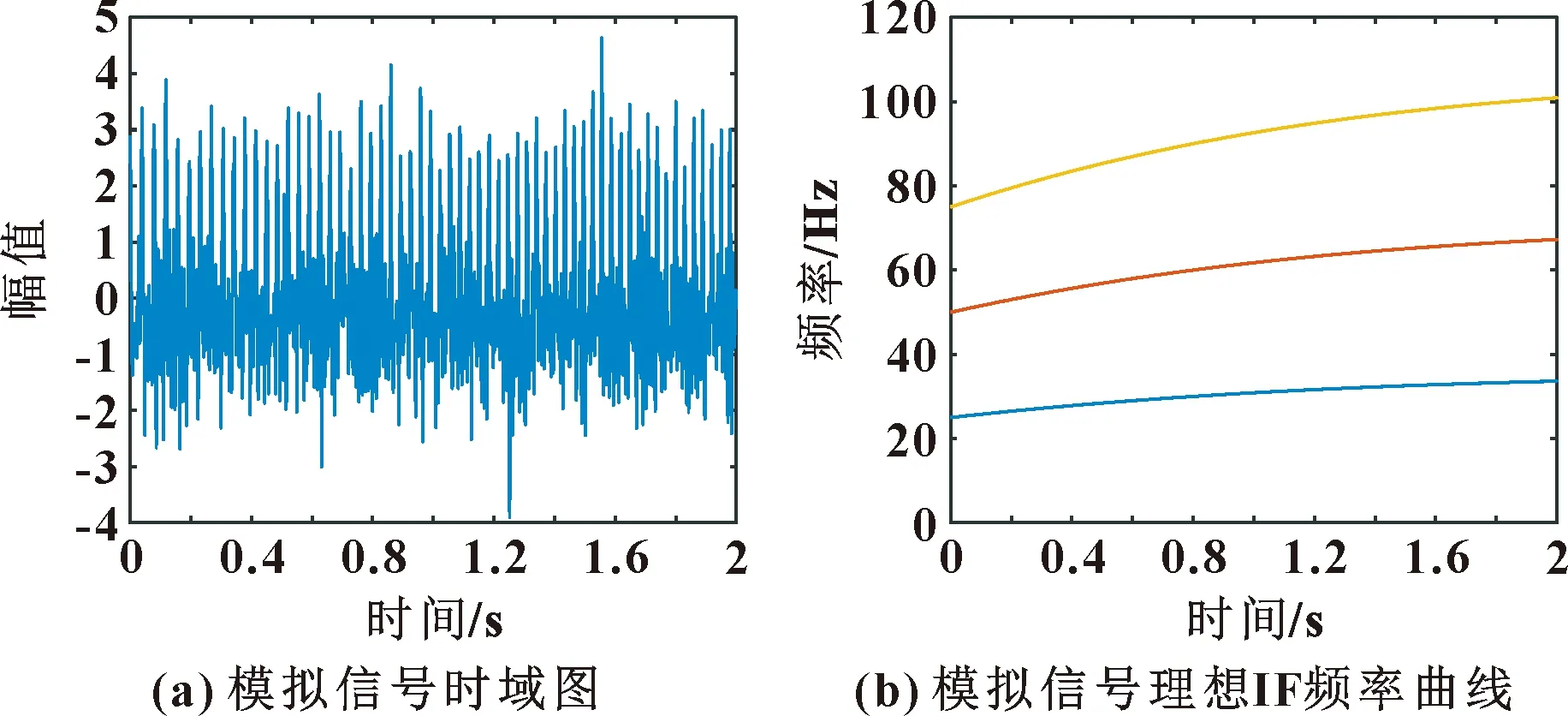
圖3 模擬信號時域圖及其理想IF曲線

分別使用STFT、CT的時頻分析方法對模擬信號進行分析，其計算結果如圖4所示。相比于STFT，CT的計算結果具有更高的時頻能量聚焦性，因此對CT進行進一步研究。

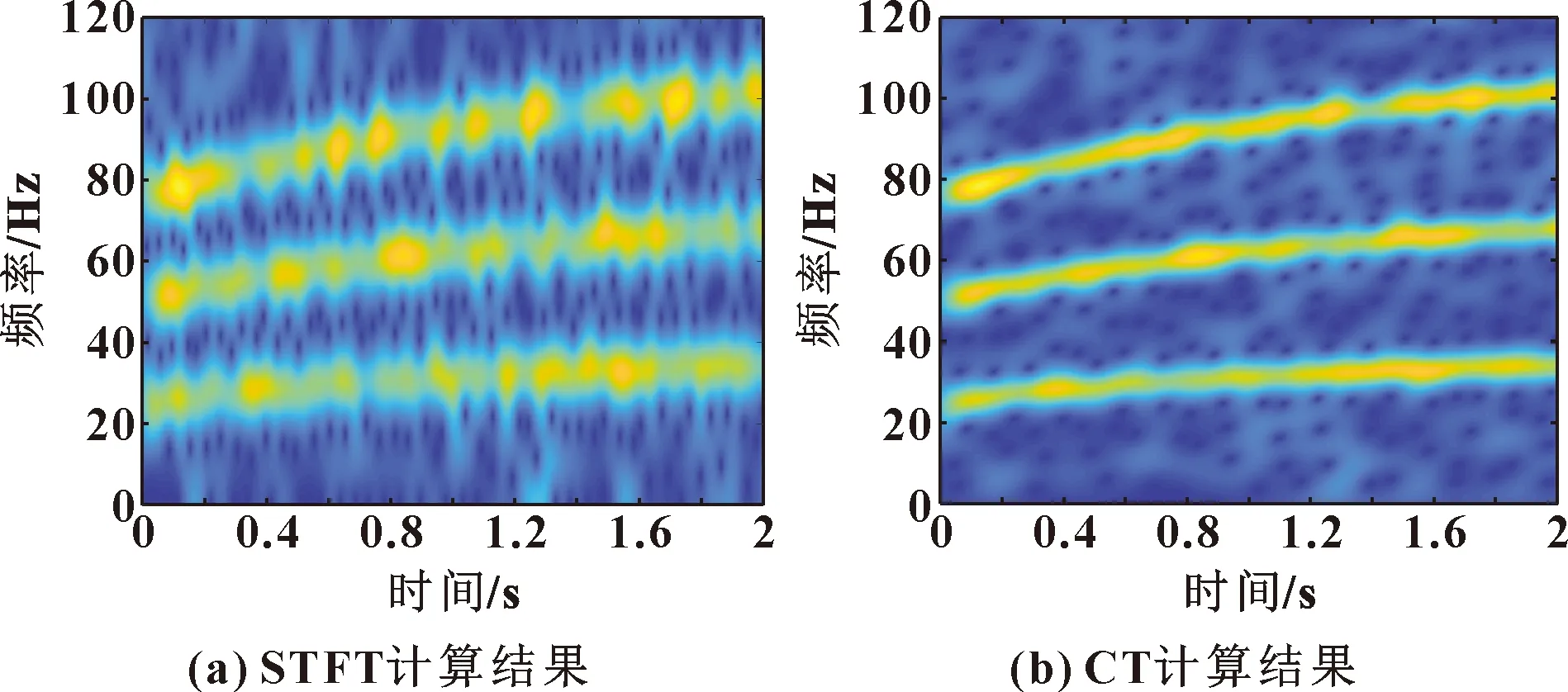
圖4 STFT及CT計算結果(數值仿真信號)

對SET算法進行改進，將原有基于STFT的SET算法改為基于CT的SET得到SECT算法。SET、SECT的計算結果如圖5所示。

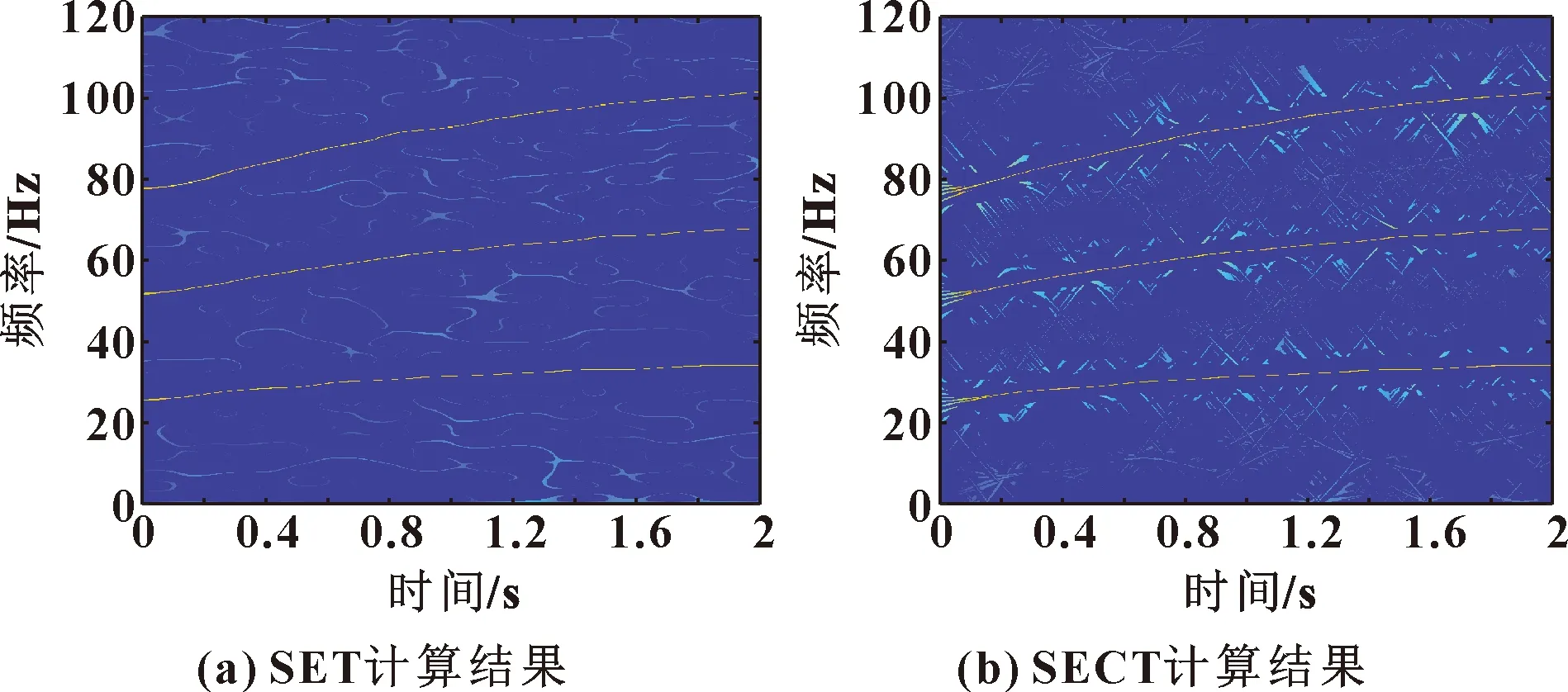
圖5 SET及SECT計算結果(數值仿真信號)

由圖5可以發現：無論是SET還是SECT，噪聲對時頻表達分辨率均有較大影響，存在不同程度的時頻模糊現象。對比圖3(b)，圖5均不能獲得理想的時頻表達，存在著時頻脊線能量發散甚至脊線扭曲失真的問題。為增強時頻聚焦性，進行更加準確的瞬時頻率估計，利用文中所提出的SECT2算法對數值仿真信號進行分析，結果如圖6所示。

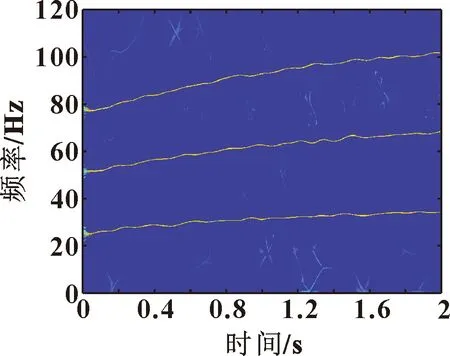
圖6 SECT2計算結果(數值仿真信號)

通過觀察以上幾種方法的計算結果，SECT2計算的結果時頻聚焦性最好，且脊線能量較高，脊線形狀與圖3(b)所示理想IF曲線最符合。各種方法的Renyi熵對比如表1所示。Renyi是一種衡量時頻面能量聚集程度的指標，其值越低表明該處理結果脊線的能量越集中，SECT2方法的時頻處理結果具有最集中的能量，驗證了所提方法具有較好的有效性與先進性。

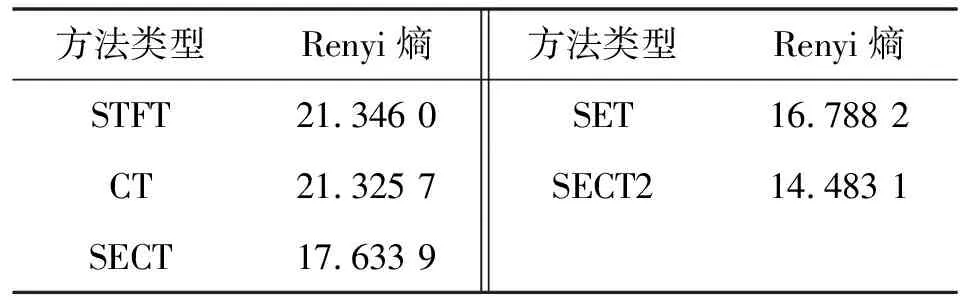
表1 幾種方法計算結果的Renyi熵比較(數值仿真信號)

3 試驗數據分析

3.1 蝙蝠信號分析

以萊斯大學(Rice University)記錄的蝙蝠信號為例，該信號的采樣頻率為140 kHz，時域圖、頻譜如圖7所示。對它進行STFT、CT計算，結果如圖8所示。兩種時頻處理方法能量均過于分散，但相比之下CT方法計算結果比STFT方法計算結果好。

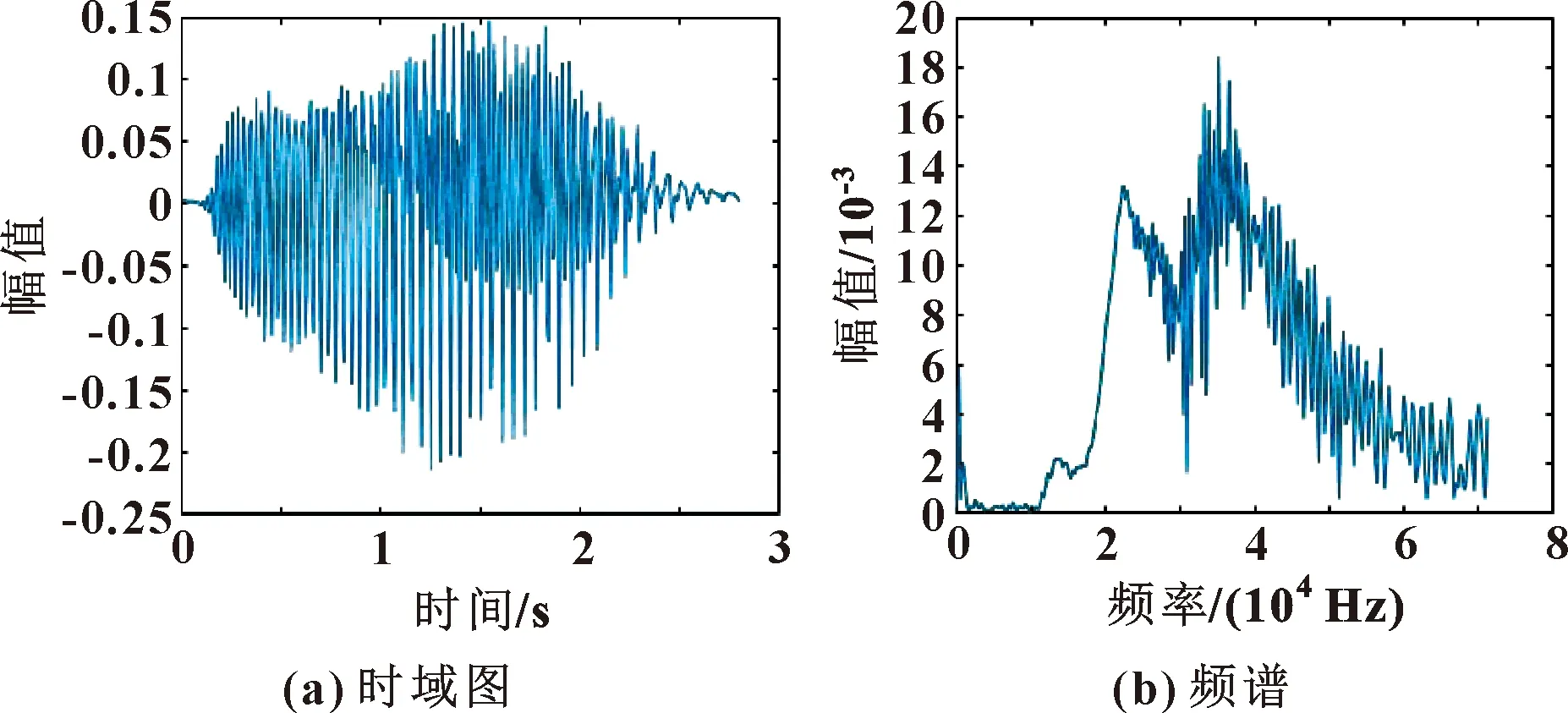
圖7 蝙蝠數據時域圖及頻譜

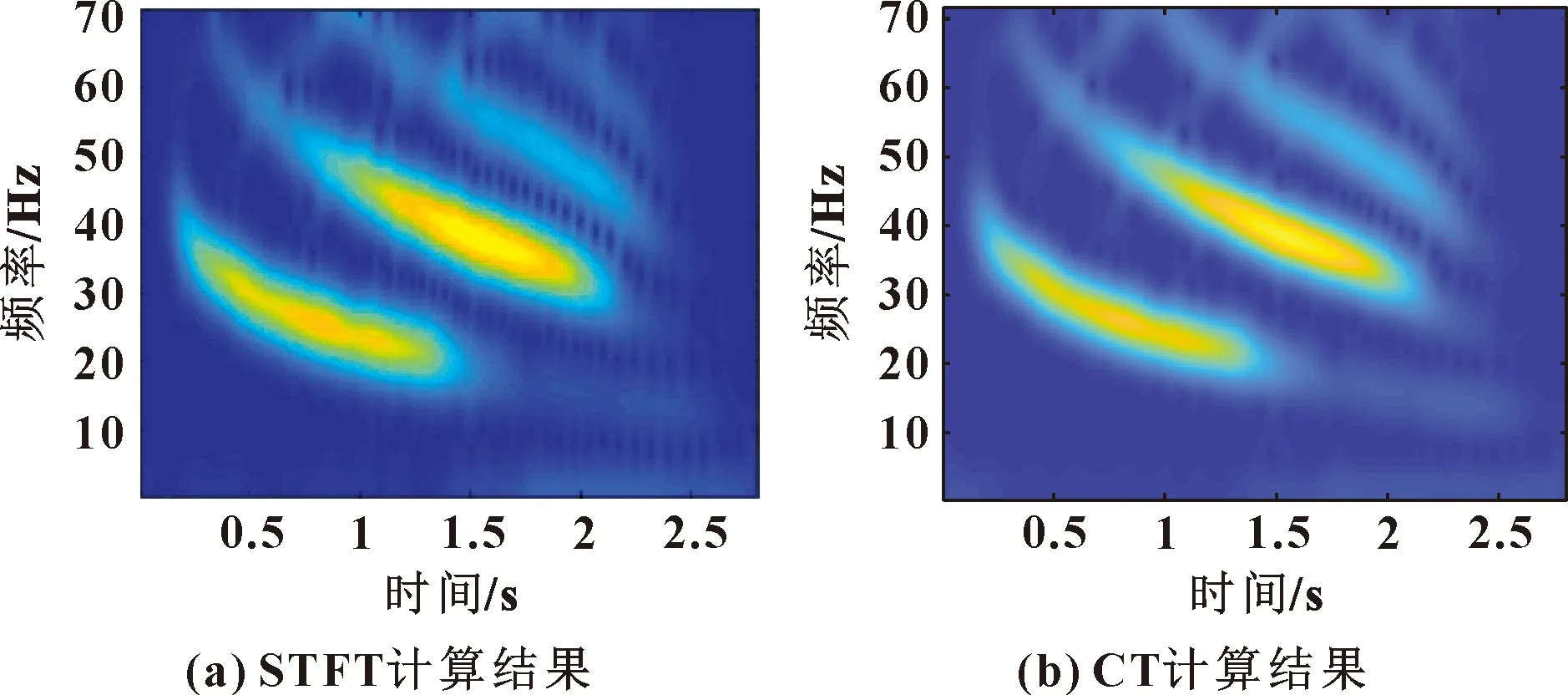
圖8 STFT及CT計算結果(蝙蝠信號)

在STFT、CT方法的基礎上，利用SET、SECT方法對蝙蝠信號進行處理，結果如圖9所示。可知：SECT能量發散，不能很好地反映多組分信號時頻脊線。利用SECT2方法對蝙蝠信號進行處理，結果如圖10(a)所示，顯然其時頻能量的聚集性更好。

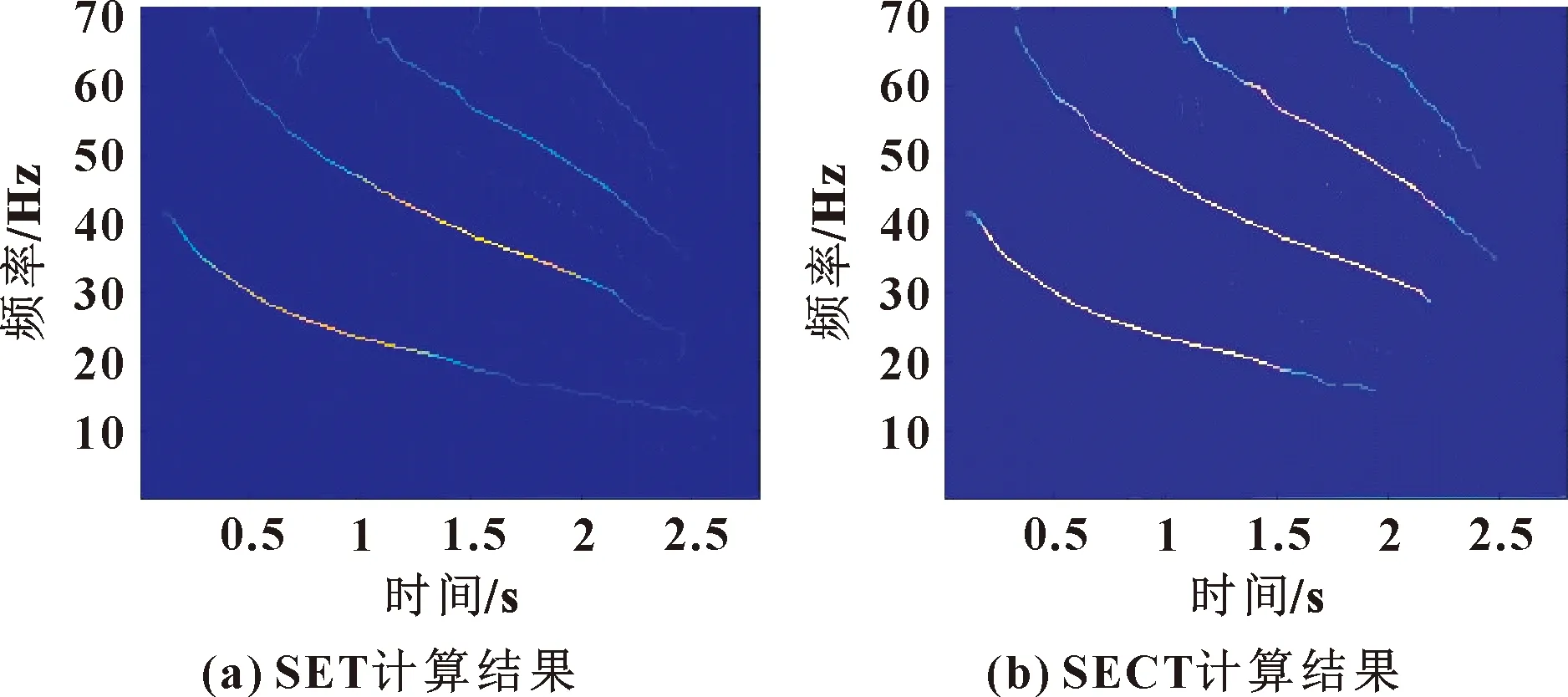
圖9 SET及SECT計算結果(蝙蝠信號)

對SECT2計算結果作脊線提取，結果如圖10(b)所示，可知所提出方法能夠較好提取蝙蝠信號中包含的脊線信息。表2所示為幾種方法的Renyi熵值比較，結果表明SECT2方法計算結果的時頻面上噪聲干擾信息較少，具有更好的多組分信號時頻分析能力。

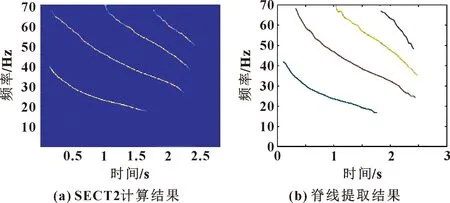
圖10 SECT2計算結果及其脊線提取結果

表2 幾種方法計算結果的Renyi熵比較(蝙蝠信號)

3.2 試驗臺故障數據分析

為驗證所提出的SECT2方法的有效性，以實驗室軸承-齒輪故障綜合試驗臺進行測試和分析。試驗臺及其結構簡圖如圖11所示，其中測點處為可更換的故障軸承，軸承故障類型為外圈故障。為模擬變轉速工況，試驗轉速從0加速到1 000 r/min，并經過一段時間恒轉速運行，最終減速到0，采樣頻率設置為2 560 Hz。測量得到的原始振動信號時域圖及頻譜如圖12所示。

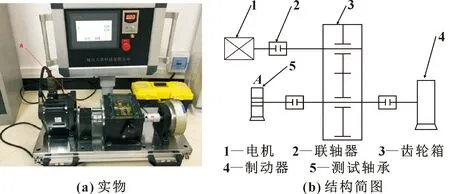
圖11 試驗臺實物圖及其結構簡圖

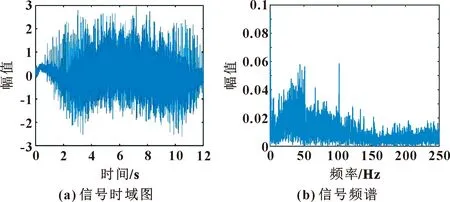
圖12 試驗臺振動信號時域圖及頻譜

由于試驗臺模擬變轉速工況，從圖12(b)中的頻譜圖中無法反映出時變的故障特征信息。對采集的信號作STFT及CT分析，結果如圖13所示。可知：STFT的時頻模糊現象很明顯，噪聲隨機地分布于時頻平面，無法正確識別時變故障特征；相比之下，CT的結果較好，其時頻脊線的能量較高，但仍然很發散，難以進行脊線提取。利用所提出的SET及SECT對振動信號進行分析，結果如圖14所示。

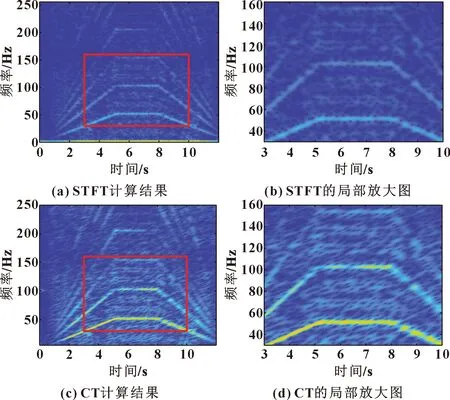
圖13 STFT及CT計算結果(試驗臺信號)

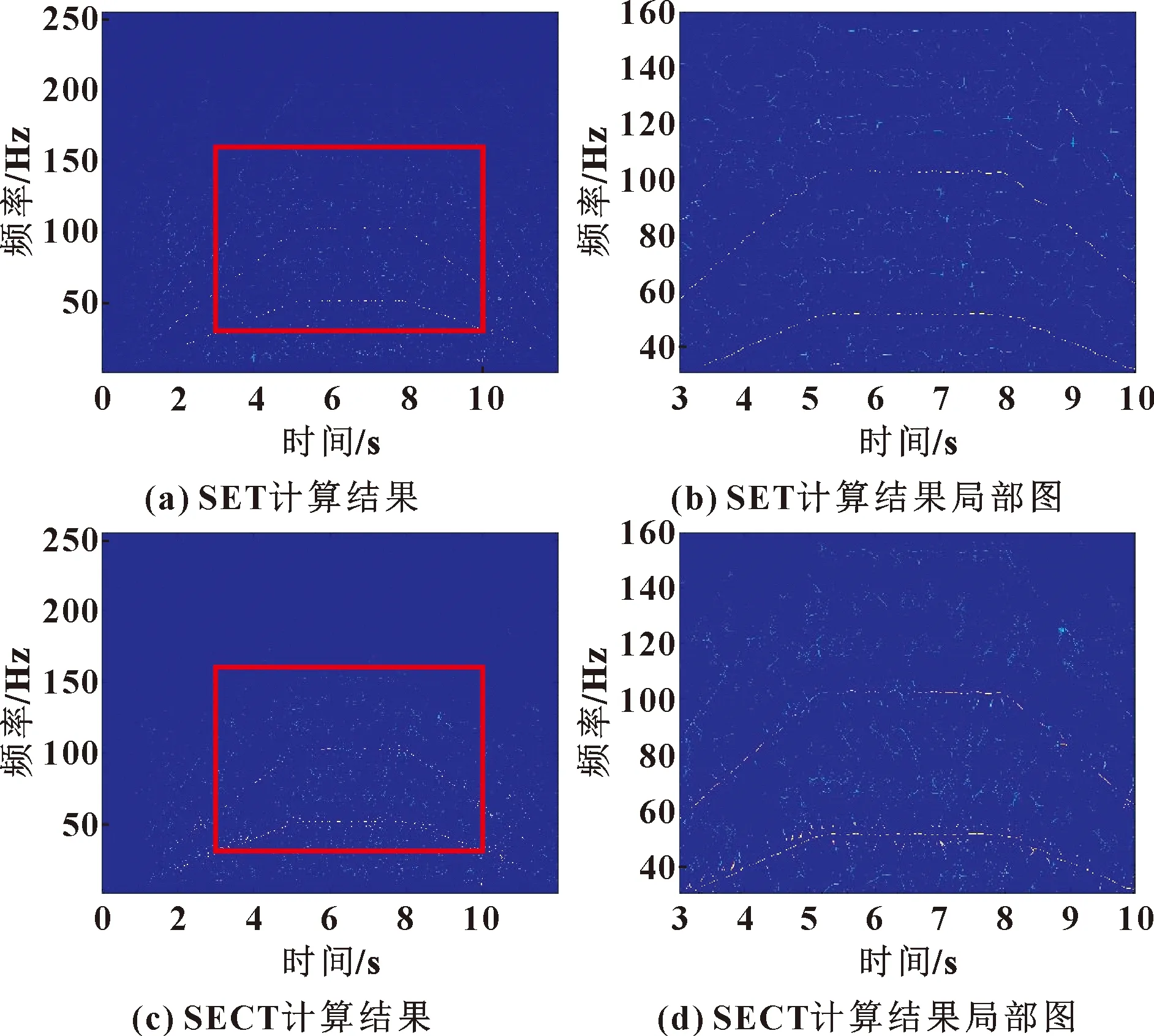
圖14 SET及SECT計算結果(試驗臺信號)

對比計算結果可知：SET、SECT方法時頻表達效果較STFT和CT有所提升，但依然存在時頻脊線能量不集中問題，在100～150 Hz之間有嚴重的能量發散現象，無法從時頻圖中有效地識別故障特征，導致時頻分析的效果欠佳。利用所提出的SECT2方法進行進一步處理，使其時變信號的能量進一步集中，相應的處理結果如圖15所示。

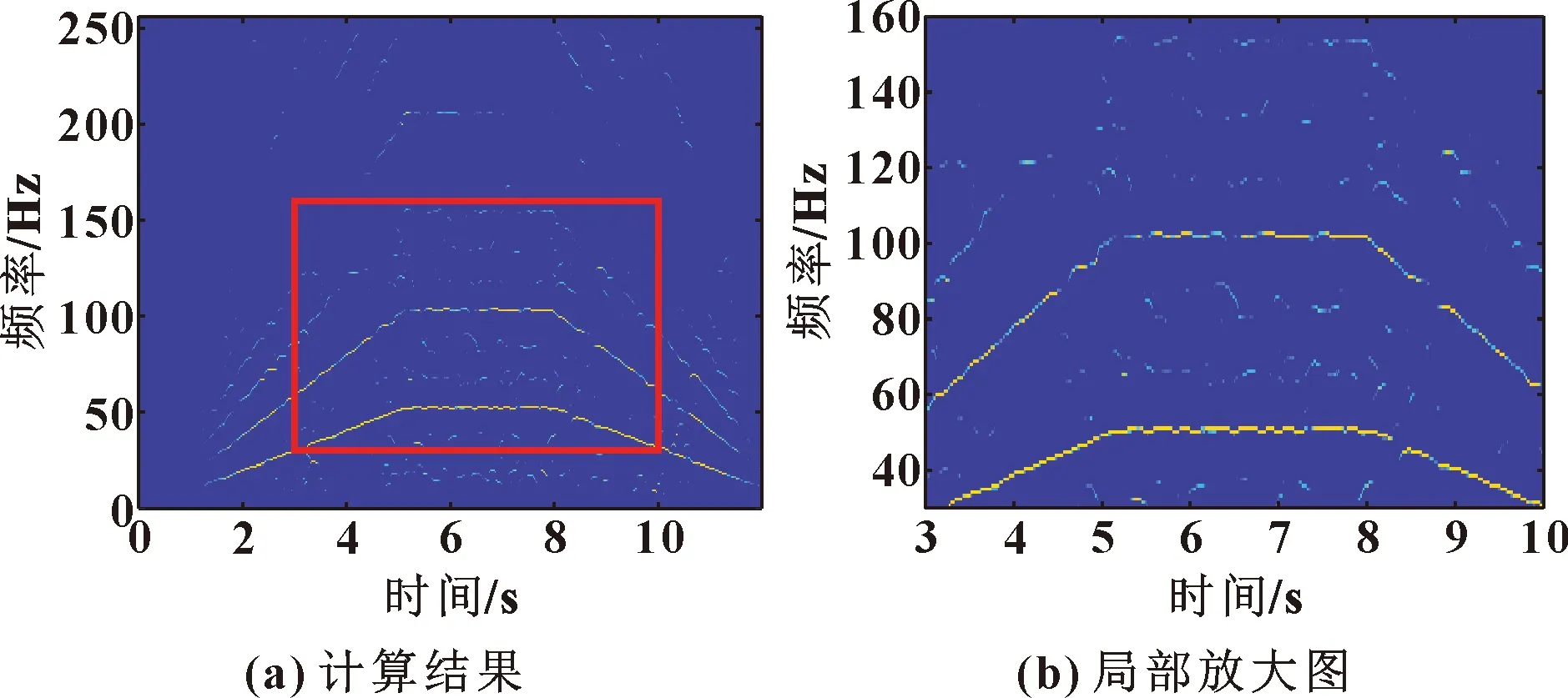
圖15 SECT2計算結果(試驗臺信號)

對比圖14和圖15可知，SECT2方法處理結果相比于SET和SECT，其時頻表示的分辨率明顯增強，時頻脊線更加集中，且有效地解決了能量發散問題。上述幾種方法的Renyi熵比較如表3所示。可知：SECT2具有最小的Renyi熵，說明它具有最高能量的時頻脊線，且能量集中程度最佳。

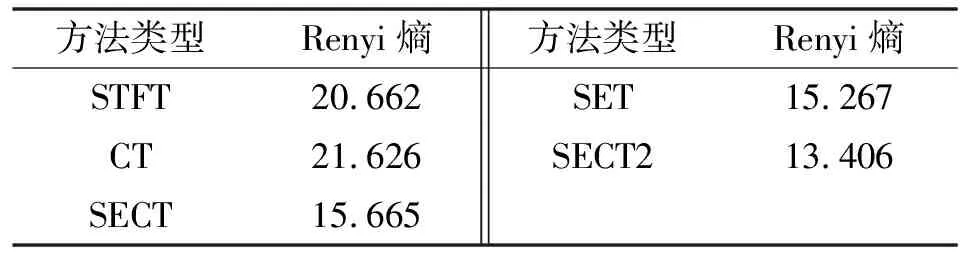
表3 幾種方法計算結果的Renyi熵比較(試驗臺信號)

對SECT2方法處理結果進行脊線提取，結果如圖16所示。從圖中可以很清晰地識別到故障特征頻率及其2倍頻。通過安裝轉速傳感器，實際測量得轉頻曲線為0遞增到16.6 Hz，再遞減至0。根據圖15中提取的故障特征頻率曲線為0遞增到53 Hz，再遞減至0，故障特征頻率(FCF)曲線為轉頻曲線的3.2倍。根據軸承動力學特征，利用外圈故障計算公式：=04××=3.2，可以判斷故障為軸承外圈故障，驗證了所提方法對變轉速下軸承故障診斷的有效性。

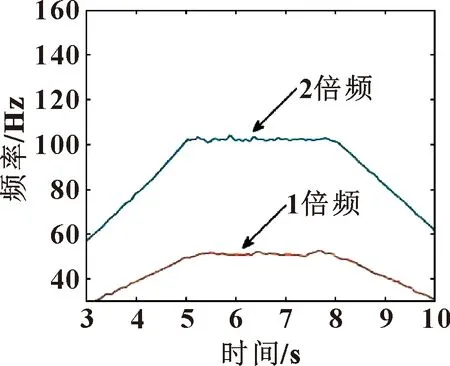
圖16 SECT2方法脊線提取結果

4 結論

基于同步提取理論，本文作者結合Chirplet變換，推導同步提取Chirplet變換公式，進一步地，對瞬時頻率進行二階估計，提出了二階同步提取Chirplet變換，用于實現噪聲干擾下的多組分信號高分辨率表達。與基于STFT的標準SET進行了對比，所提出的SECT2具有更強的時頻脊線聚焦性，可獲得比SET更集中、更高能量的時頻脊線。通過蝙蝠信號、試驗臺測量信號對所提方法進行驗證，結果表明SECT2方法具有更好的時頻分析能力。