基于雙穩態非線性能量阱的軸承-軸懸臂系統振動抑制研究
溫曉蕾,李妙玲,陳智勇,,徐穎強,姚永玉
(1.河南水利與環境職業學院 土木工程系,鄭州 450008;2.洛陽理工學院 智能制造學院,河南 洛陽 471023;3.西北工業大學 機電學院,西安 710072)
隨著科學技術的發展,對軸承的振動質量提出了更高要求。如何降低工作中軸承的振動,是軸承應用領域的重要技術難題。利用吸振技術對配套主機進行振動控制是有效的振動抑制手段,但目前傳統吸振器吸振頻帶狹窄,對寬轉速軸承減振效果不明顯。
國內外學者針對基于能量阱的減振控制進行了大量的研究:20世紀中葉,文獻[1]提出吸振器添加非線性剛度元件——非線性能量阱(Nonlinear Energy Sink,NES)進行振動控制,非線性能量阱可有效拓寬減振頻帶,且附加質量小,穩定性好;文獻[2]對NES靶能量傳遞進行了深入研究,證明系統能量可單向傳遞至NES中,且其具備附加質量小,減振頻帶寬,可靠性高等優點;文獻[3]證明能量阱可以快速吸收耗散梁的大部分振動能量,并基于能量耗散率優化了能量阱在梁上的安裝位置;文獻[4]將能量阱附加在機械臂上,利用數值法分析了能量阱的工作性能;文獻[5]研究表明,能量阱可以有效抑制星載飛輪在瞬態激勵和穩態激勵下的振動;文獻[6]利用振子內部旋轉設計了一種能量阱,與純立方剛度能量阱的對比表明該結構具備更好的減振性能及穩定性;文獻[7]研究了沖擊載荷下能量阱的減振性能,結果表明能量阱能使船艦快速減振,但能量阱對沖擊強度較為敏感,只有達到觸發閾值時才可高效減振;文獻[8]將能量阱安裝在夾層梁內,研究能量阱對梁的振動抑制,結果表明減小能量阱阻尼可提高其工作性能;文獻[9]研究了受控系統在附加能量阱后產生高分支響應的條件,并通過串聯能量阱在一定范圍內消除高分支響應,提高了能量阱在不同激勵強度下的減振穩定性;文獻[10]基于分段線性構造了非光滑非線性恢復力,建立了軸承系統耦合NES的力學模型,利用遺傳算法對NES的結構參數進行了優化,分析了多自由度系統參數的優化問題,試驗結果表明,優化后的NES可在更寬的頻帶內對軸進行振動抑制;文獻[11]以能量阱耗散為工作性能指標,分析了能量阱在沖擊激勵下的減振性能,并研究了能量阱結構參數對觸發閾值的影響,結果表明提高非線性剛度可以降低能量阱觸發閾值,但非線性剛度過大,會造成強激勵下能量阱性能下降;文獻[12]研究了在諧波激勵下受控系統安裝能量阱及壓電俘能器時振動控制與能量收獲的集成問題,并分析了共振附近的準周期運動對振幅、能量收集帶寬的影響;文獻[13]利用數值仿真分析了雙穩態能量阱各個結構參數對其減振性能的影響,通過對能量阱結構參數的逐次優化,得到了質量比以及調諧頻率比的最佳區間,同時兼顧了能量阱減振性能及能量俘獲,且只有當外界激勵強度達到一定程度時,能量阱才能高效工作。
綜上分析,如何降低NES觸發閾值,提高NES在低擾動工況下的工作性能具有重要研究意義。雙穩態非線性能量阱(Bistable Nonlinear Energy Sink,BNES)的非線性剛度由立方剛度及負剛度構成,可降低能量阱的觸發閾值,提高其在低擾動下的工作性能。本文利用線性剛度元件,通過非線性幾何關系構建BNES,并耦合于懸臂梁系統進行減振分析;通過數值計算,利用勢能函數分析NES觸發閾值與非線性剛度比的關系,研究BNES的瞬態、穩態工作性能。
1 軸承系統耦合BNES模型構建
BNES由質量單元、阻尼單元、非線性剛度及負剛度組成。文中利用線性元件,通過幾何非線性關系構造非線性恢復力以實現非線性剛度,如圖1所示。

圖1 非線性剛度實現
振子在位置3利用2個剛度系數相同的線性彈簧連接,此時為預緊狀態;位置1,2為兩彈簧自由狀態。當振子離開位置3時,可得恢復力F與位移x的關系為
(1)
式中:F為位移x方向的恢復力;k為彈簧的剛度系數;x為偏離位置3的位移;L為彈簧原長;s為振子位于位置3時,彈簧處于壓縮狀態下的長度。利用麥克勞林公式把(1)式展開為
(2)
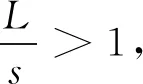
F≈-K1x+K3x3,
(3)
當振子的位移滿足|x|≤0.4s時,(3)式的誤差不高于5%[14]。
將上述BNES安裝于軸承系統(即主系統)中,如圖2a所示,并將系統簡化為如圖2b所示的二自由度模型。
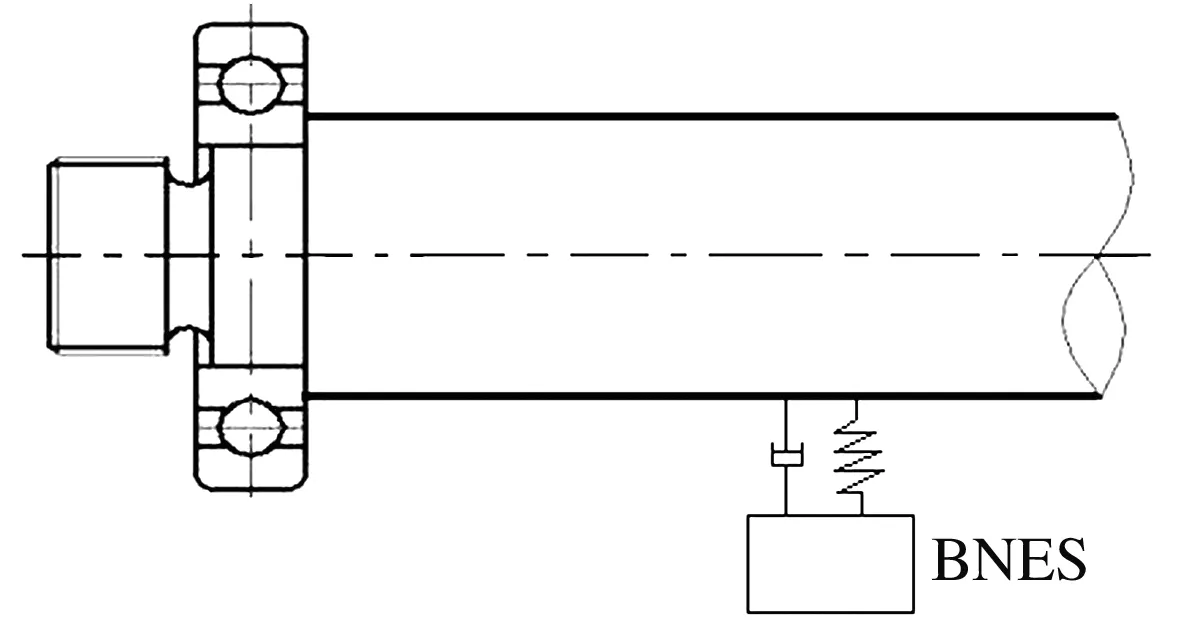
(a)軸承系統安裝能量阱示意圖
外界激勵下系統的動力學方程為
,(4)
式中:mn,m分別為能量阱和軸的等效質量;Cn,C分別為能量阱和軸的等效阻尼;K1,K3分別為能量阱負剛度和立方剛度;K為軸的等效剛度;X,Y分別為能量阱和軸的位移;F(t)為激勵。
諧波激勵Fcos(ωt)下,對(4)式進行量綱一化得
,(5)
ζn=Cn/(2mnωn),ζ=C/(2mωn),
τ=ωnt,k1=K1/K,k3=L2K3/K,
x=X/L,y=Y/L,f=F/(KL),μ=mn/m,
式中:ω,ωn分別為外界激勵頻率、主系統固有頻率;t為時間。
2 平衡點穩定性分析
本節利用勞斯-赫爾維茨法則對系統的平衡點進行分析。
首先,取x1=x,x2=y,x3=x′,x4=y′,則(5)式的一階微分形式表示為
(6)
由(5)式可知
(7)
令
(8)
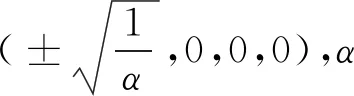
由(5)式可求得平衡點(0,0,0,0)對應的雅可比矩陣為
(9)
對應的特征方程為det(J1-λI)=0,則
a0λ4+a1λ3+a2λ2+a3λ+a4=0,
(10)
a0=1,a1=2ζ+4ζn,
根據勞斯-赫爾維茨可知,(8)式由上述特征系數組成的勞斯-赫爾維茨行列式為
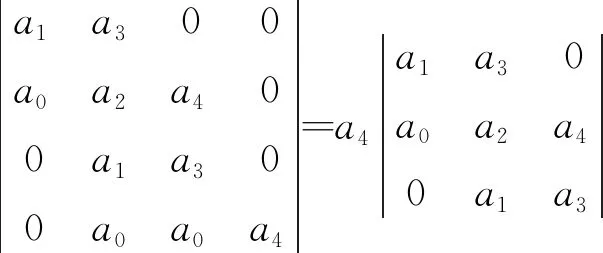


(11)
對應的特征方程為det(J2-λI)=0,則
b0λ4+b1λ3+b2λ2+b3λ+b4=0,
(12)
b0=1,b1=2ζ+4ζn,
Δ1=b1=2ζ+4ζn>0,
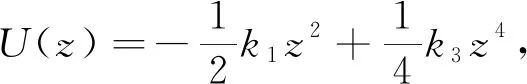
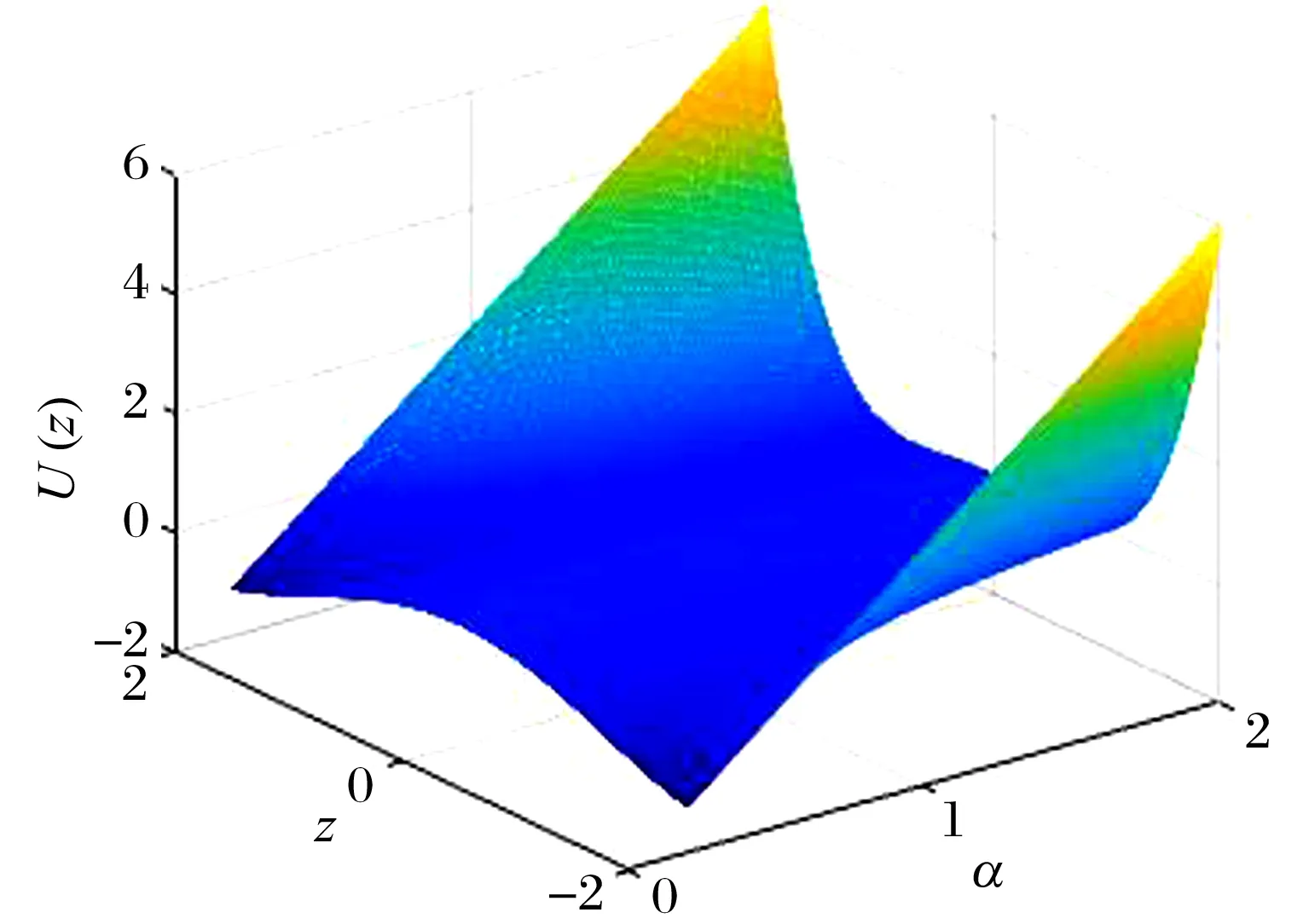
圖3 非線性剛度比對勢能函數的影響
由圖3可知,勢能函數存在1個勢壘和2個勢阱,在BNES跨過勢壘做阱間大幅振蕩時,BNES高效減振,且勢阱深度隨非線性剛度比α的變大而降低,故通過調節非線性剛度比可以控制勢阱深度,進而改變BNES的觸發閾值。
3 BNES減振性能分析
3.1 瞬態減振性能分析
利用集中參數模型,根據(5)式建立的二自由度動力學方程,分析BNES的減振性能。系統中參數設置為:μ=0.05,ζn=0.01,k1=0.1,k3=1,ζ=0.05,ωn=2rad/s,主系統初始條件為x(0)=y(0)=x′(0)=0,y′(0)=0.45,對所有物理量進行量綱一化處理,并利用四階龍格庫塔法進行數值分析。
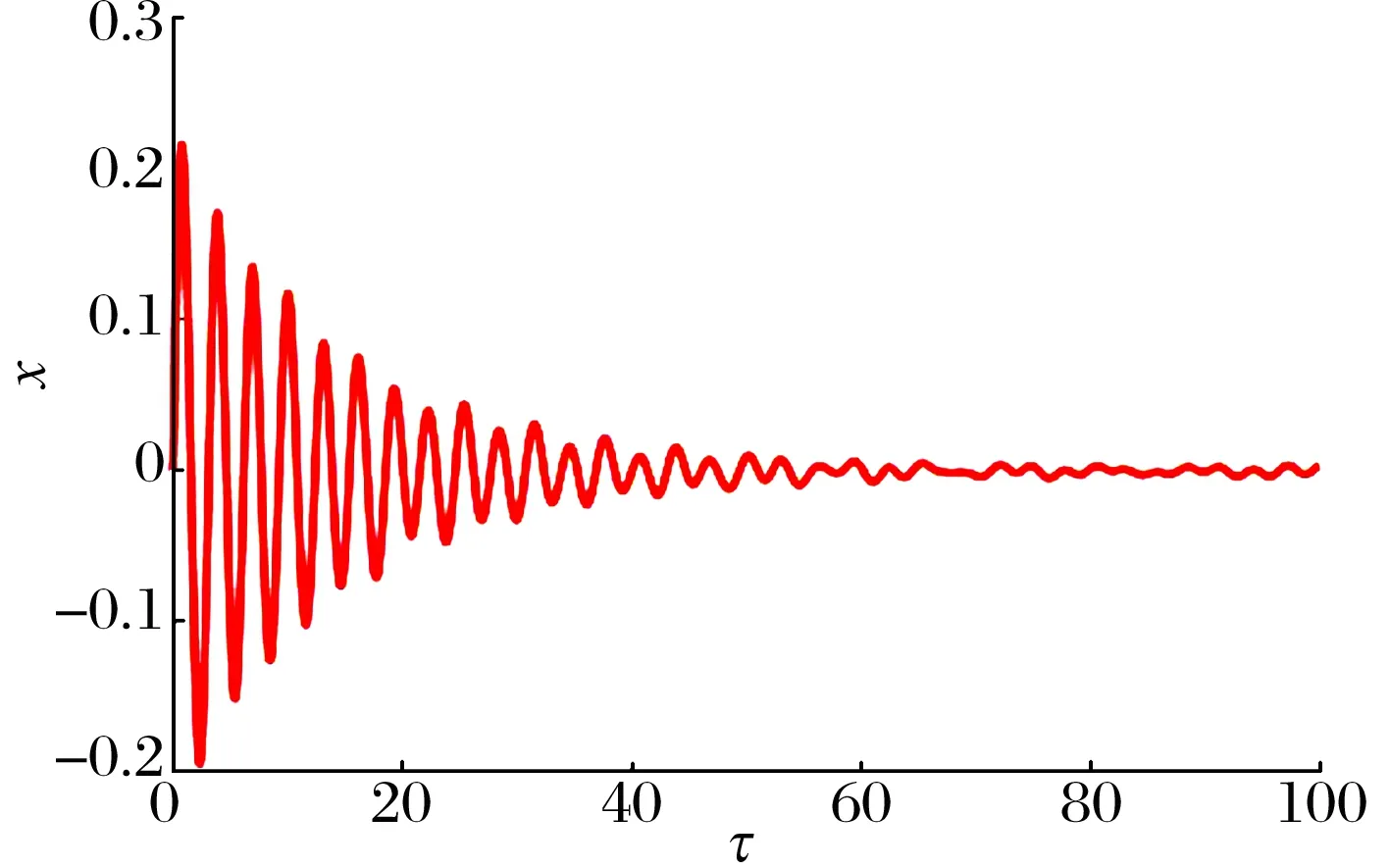
為表明BNES的減振性能,對比分析了有無安裝能量阱時主系統的時域響應,結果如圖4、圖5所示。由圖4可知,在初始條件下,主系統隨時間做衰減振動,利用本身阻尼耗散初始能量,至τ=100時,主系統仍有較大振幅。由圖5可知,在BNES作用下,主系統振動快速衰減,在約τ=50時,振幅趨于0。
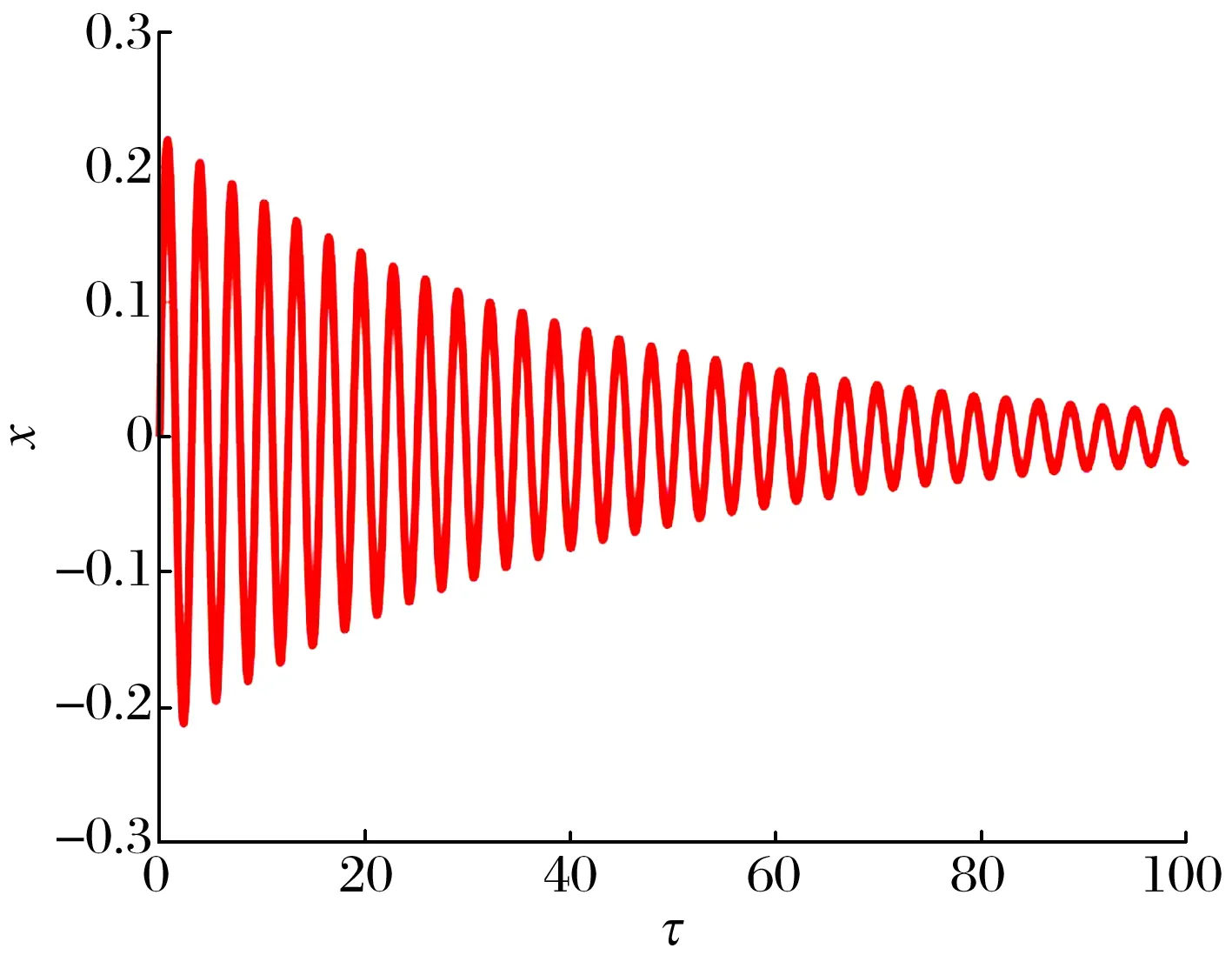
圖4 無BNES時主系統的時域圖
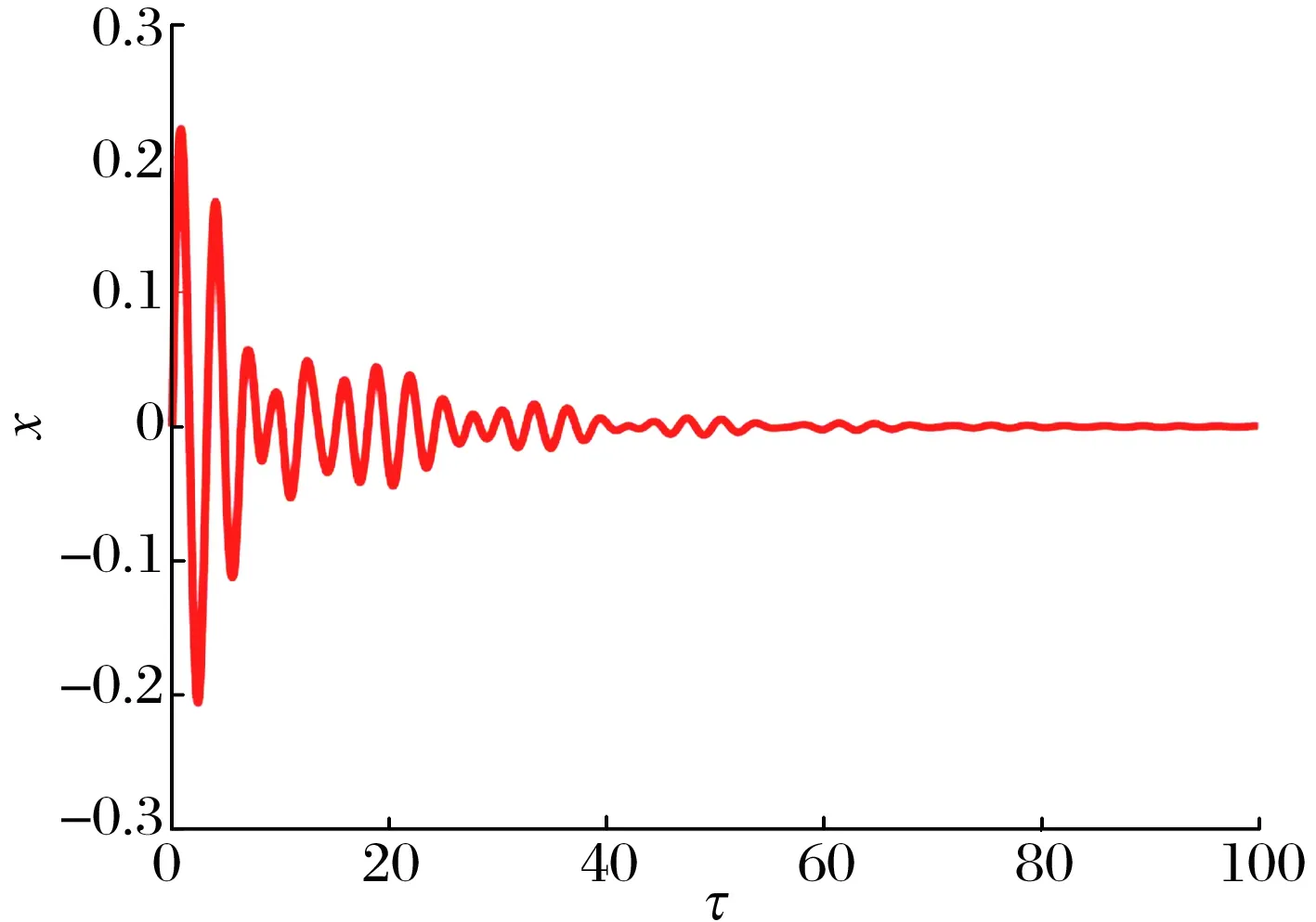
(a)主系統的時域圖
主系統與BNES的小波圖如圖6所示,τ=0至τ=19間主系統和BNES發生1∶1共振及諧波共振,在τ=36時主系統振幅接近零。
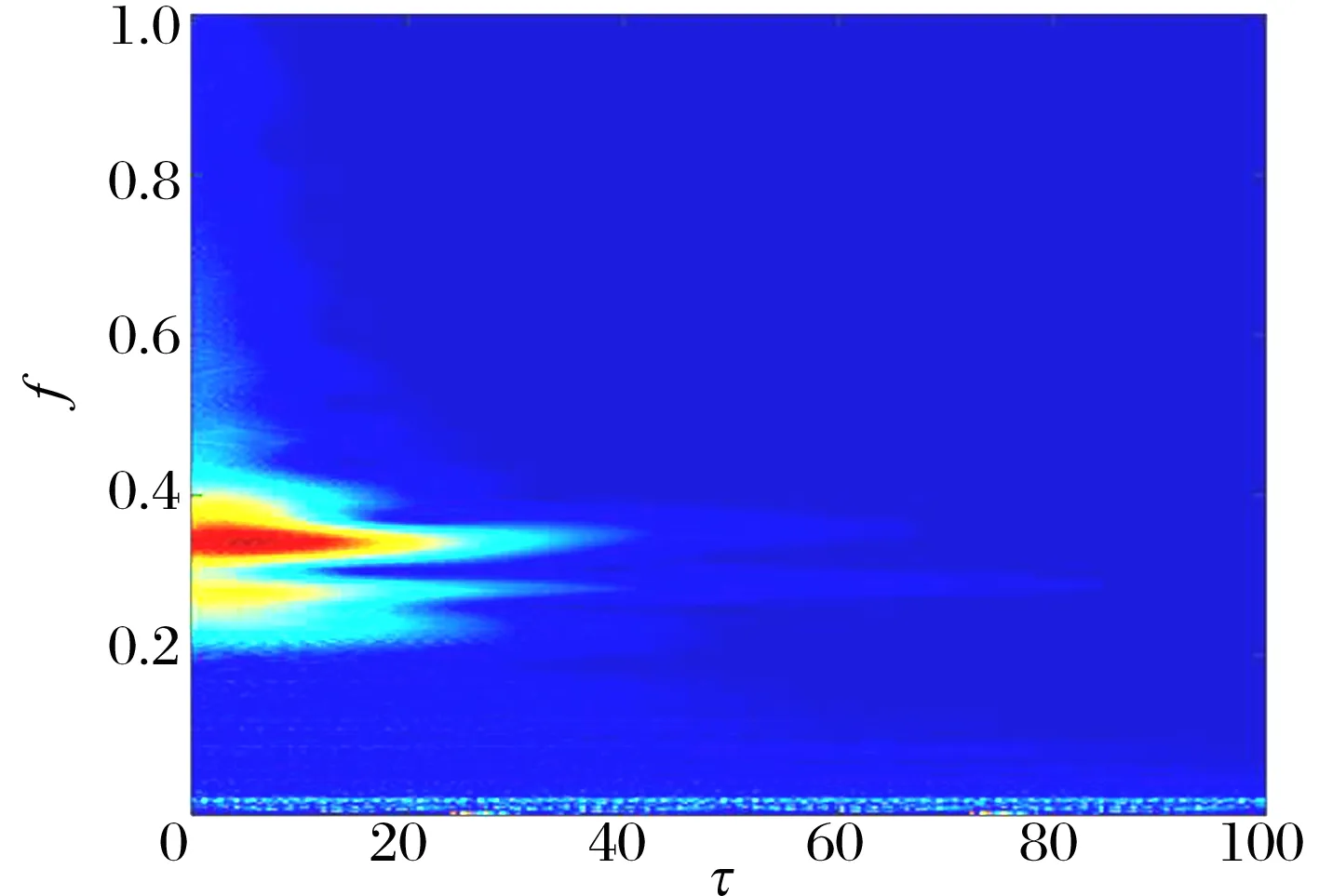
(a)主系統小波圖
為對比分析BNES與NES在相同工況下的減振效果,取相同系統參數和初始條件,分析NES作用時主系統和NES的振動情況,結果如圖7所示。由圖可知,對同一系統,在相同激勵條件下,NES對主系統有一定減振作用,系統部分振動能量在NES中消耗,但由小波圖可知,主系統在τ=60附近仍有較大能量,因此BNES的減振效果更好。
(a)主系統的時域圖
3.2 穩態減振性能分析
利用四階龍格庫塔法,在諧波激勵下對BNES進行穩態性能分析。分析中系統參數與之前保持一致,激勵為F(t)=0.1cos(1.5τ),初始條件為x(0)=y(0)=x′(0)=y′(0)=0,仿真結果如圖8所示。同時,為對比BNES和NES的減振效果,相同條件下分析NES作用時的運動情況,結果如圖9所示。BNES及NES在相同系統參數及外界激勵條件下與主系統的相對速度關系如圖10所示。
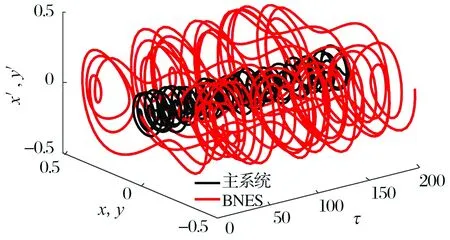
圖8 BNES減振性能

圖9 NES減振性能
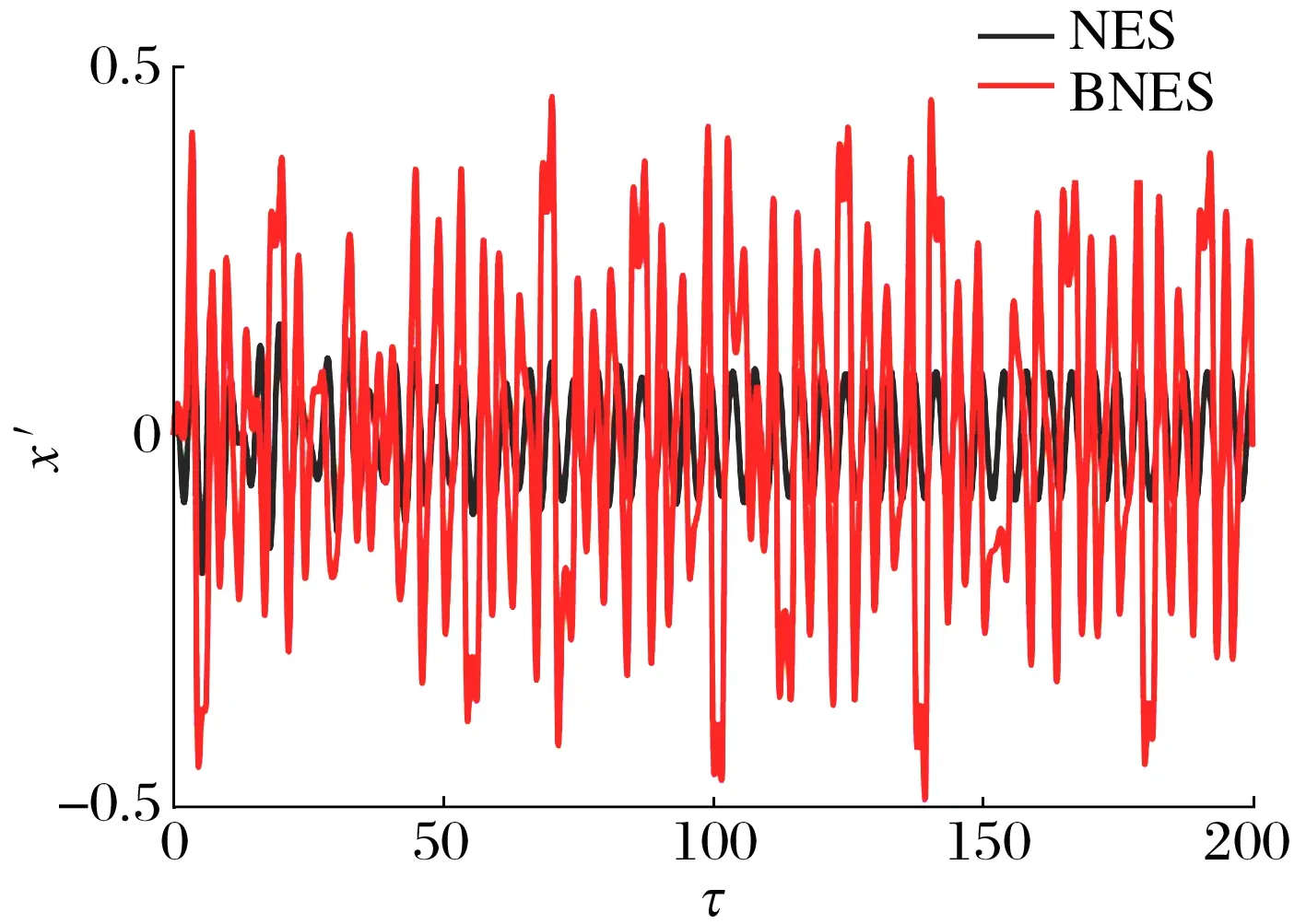
圖10 BNES及NES在相同系統參數及外界激勵條件下與主系統的相對速度
對比圖8和圖9可知,在相同系統參數及外界激勵條件下,BNES振動幅度遠遠大于NES;由圖10可知,BNES與主系統相對速度極值約為NES與主系統相對速度極值的3.2倍。因為能量阱消耗能量P正比于能量阱與主系統的相對速度Δv的平方[13],而BNES與主系統相對運動劇烈,可保證能量通過能量阱阻尼耗散。
4 BNES觸發閾值分析
基于能量傳遞率分析BNES在諧波激勵下的觸發閾值,系統參數仍保持不變,激勵為F(t)=fcos(2τ),初始條件為x(0)=y(0)=x′(0)=y′(0)=0。定義能量傳遞率為[7]
T(τ)={μx′2(τ)+k1[x(τ)-y(τ)]2+
(13)
式中:T(τ)為BNES在不同時刻存儲的總瞬態動能及勢能與系統瞬態總能量的比值。
分析不同激勵幅值f下BNES的能量傳遞率,結果如圖11所示:在諧波激勵幅值f=0.25時,系統能量傳遞至BNES的不足2%,絕大部分能量仍在主系統里被阻尼消耗;而在激勵幅值為f=0.30時,主系統傳至BNES的能量接近90%,大部分能量在BNES消耗。
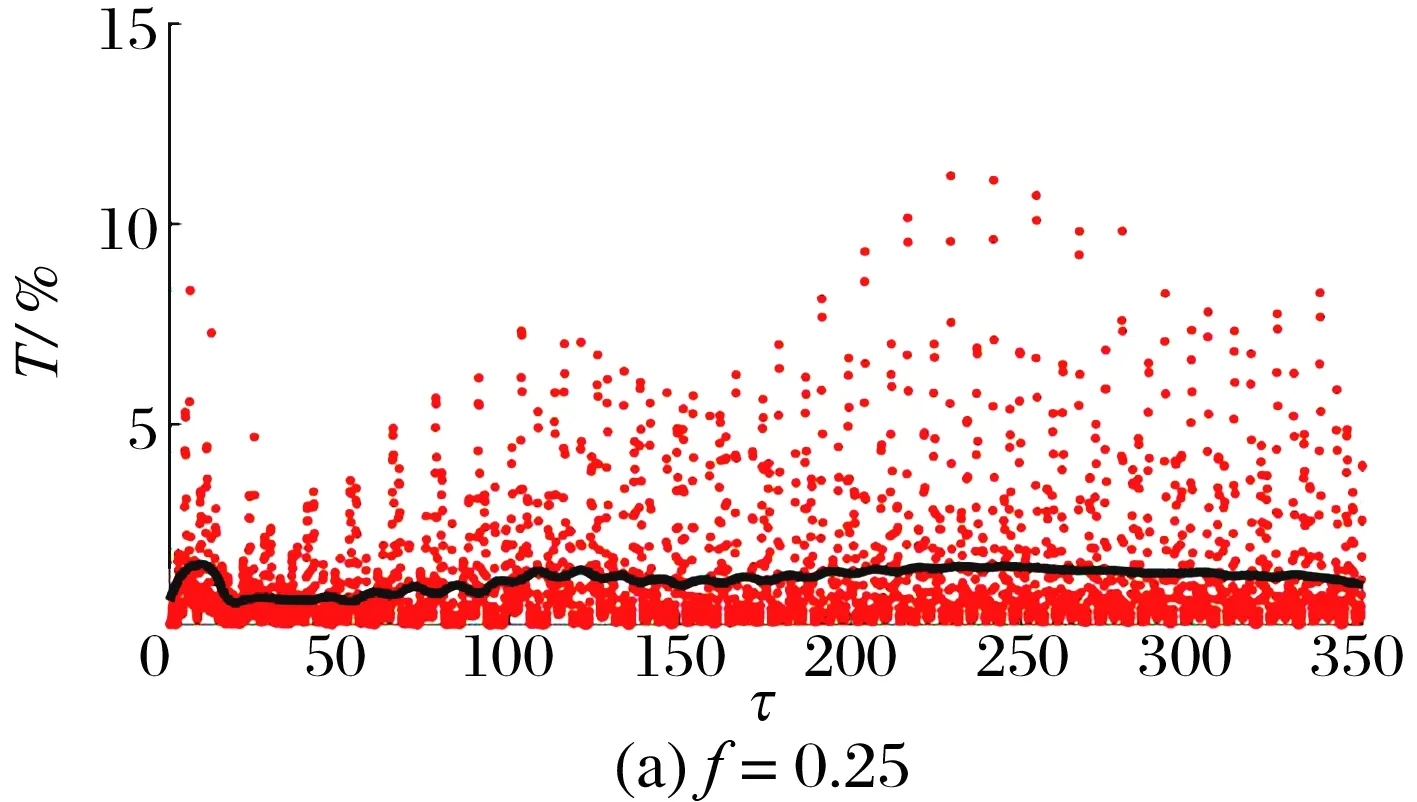
圖 11 不同激勵強度下BNES的能量傳遞率
不同激勵強度下能量傳遞率的Colormap圖如圖12所示,非線性能量阱的觸發閾值為0.29,當諧波激勵幅值不小于0.29時,BNES發生共振俘獲,實現高效減振。
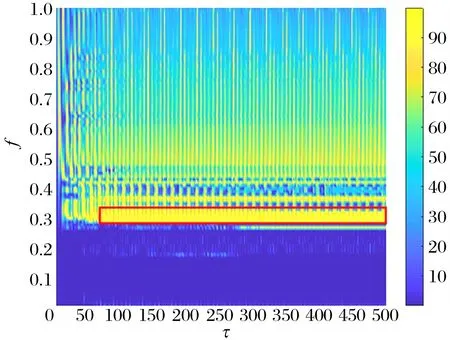
圖12 BNES能量傳遞率Colormap圖
此外,由圖12可知在非線性剛度比一定時,當激勵強度超過閾值后,隨著激勵的進一步增加,能量傳遞率相應降低。進一步做如下定義[7]
(14)
式中:En(τ)為各時刻能量阱的能量耗散率;En為穩定后能量阱的能量耗散占比;p為沖擊作用下軸的初速度,沖擊下系統總能量可表示為E=p2/2。
由(14)式可得不同非線性剛度比下BNES的能量耗散率,如圖13所示;隨著非線性剛度比的增加,觸發閾值降低,但隨著軸的初速度(激勵強度)增加,能量耗散率降低;非線性剛度比較小時,觸發閾值較大,但隨軸的初速度(激勵強度)增加,能量耗散率可保持在較高水平。

圖13 非線性剛度比對觸發閾值影響
5 結論
利用線性剛度元件,通過幾何非線性構建了BNES,得到以下結論:
1)通過勞斯-赫爾維茨法則,對平衡點進行穩定性分析,發現BNES存在1個不穩定平衡點和2個穩定平衡點。
2)通過數值方法分析了BNES的工作性能,發現相比于普通NES,BNES在低擾動下減振性能更好,更適合高精儀器低擾動下的振動控制。
3)利用能量傳遞率及能量耗散率分析了BNES的觸發閾值,發現觸發閾值與非線性剛度比存在反比例關系,在觸發閾值附近BNES能量傳遞率及能量耗散率最高,之后隨著激勵強度的增加,兩者逐漸降低。

