基于林滋泰德-龐加萊法的達芬系統(tǒng)的求解

莘智，侯瑾蓉

（內蒙古師范大學數學科學學院，內蒙古 呼和浩特 010022）

1830年，泊松在研究單擺的振動時，提出將非線性系統(tǒng)的解按小參數ε的冪次展開的近似計算方法稱為攝動法或小參數法［1］。1892年，林滋泰德為了消除在天文學中利用正規(guī)攝動法求近似解時出現的久期項問題，最先提出對正規(guī)攝動法進行改進。后來，龐加萊對改進后的方法的合理性進行了證明，故而稱為林滋泰德-龐加萊法，它的出現很好地解決了系統(tǒng)共振，即久期項問題。林滋泰德-龐加萊法認為解和系統(tǒng)的激勵頻率都是ε的未知函數，都要展成ε的冪級數形式，通過確定級數形式中的待定系數，從而求得解析解和頻率［2］。本文主要通過林滋泰德-龐加萊法對達芬系統(tǒng)的幾種振動求解，得到了精確度較高的近似解析解。

1 達芬系統(tǒng)的自由振動

達芬系統(tǒng)的自由振動動力學方程為［1］

規(guī)定初始條件為［2］

此時將該動力學方程的解展開為冪級數的形式

同時，將自由振動的頻率ω也展成ε的冪級數形式

將式（4）兩邊平方，得

將式（3）和式（5）代入式（1），引入新的自變量ψ=ωt，將原來的微分改定義為對ψ的微分，轉化為

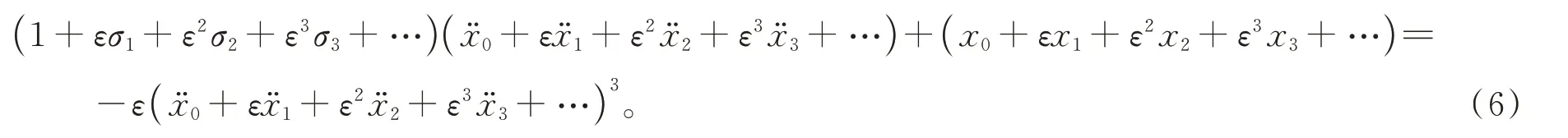
令等式兩邊ε相同次冪項的系數相等，可得方程

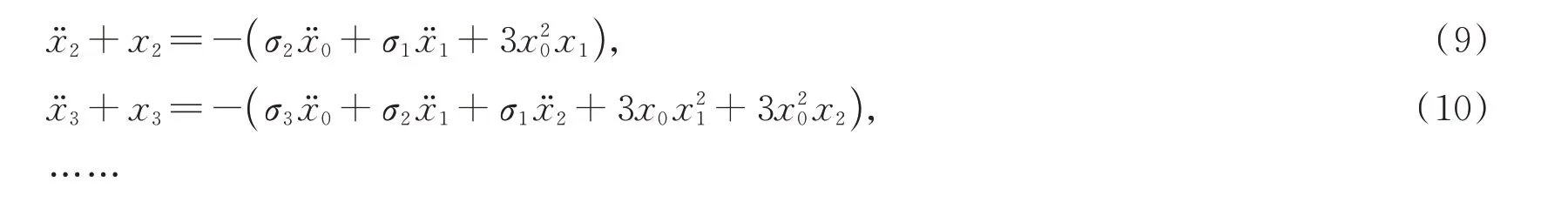
規(guī)定各方程的初始條件為

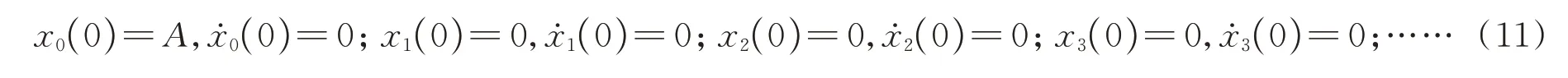
由零次近似方程（7）和初始條件可以解出

將式（12）的解代入式（8）的右邊，可得

為消除方程中出現的久期項，需要令方程右邊的cosψ項的系數等于零，于是，可以推導出

這時，在滿足此條件的基礎上解出x1的值，設

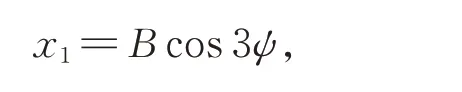
在方程（13）滿足初始條件（11）的情況下，可得方程的解為

將式（12）和式（15）代入方程（9）中，整理得

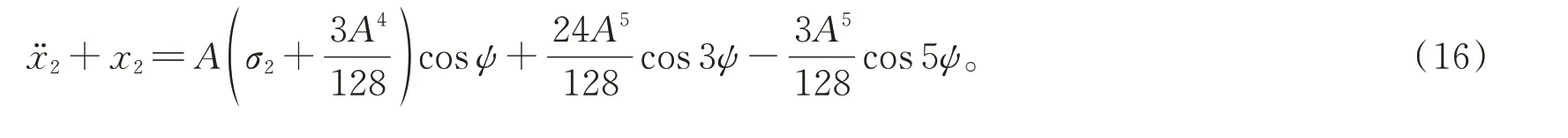
為消除方程中出現的久期項，需要令方程右邊cosψ項的系數等于零，導出

此時在滿足此條件的基礎上，設

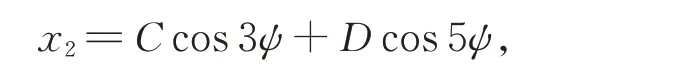
在方程必須滿足初始條件情況下，可得方程的解為

將式（12），式（15），式（18）代入方程（10）中并加以整理得

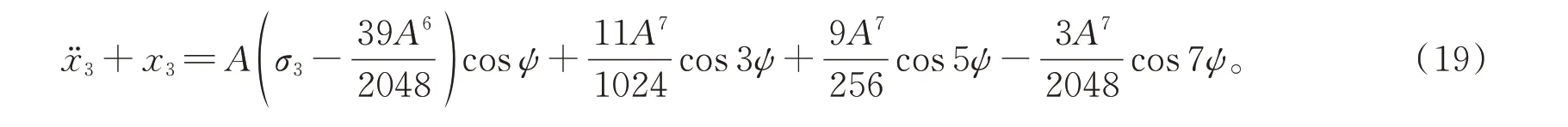
為消除方程中出現的久期項，需要令方程右邊的cosψ項的系數等于零，導出

解x3的過程與前面解x1和x2的過程相同，重復操作，可得

由此可得方程（1）的三階精度的解

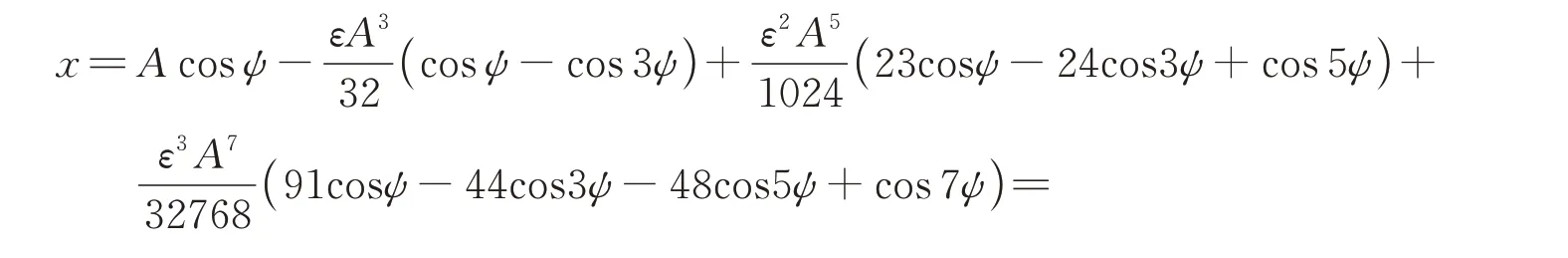
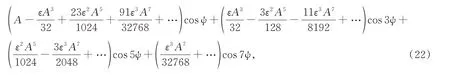
以及自由振動頻率ω的表達式

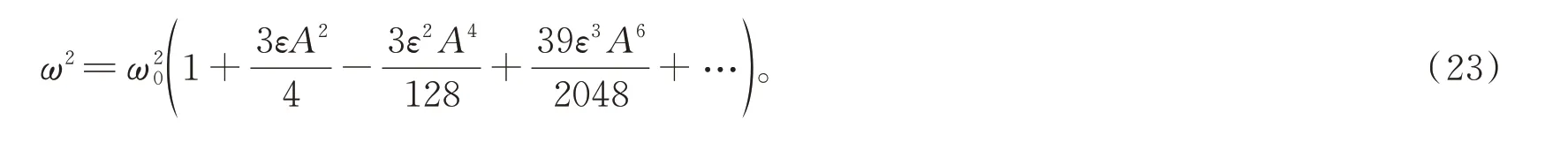
2 接近共振的受迫振動

討論帶微弱阻尼的達芬系統(tǒng)接近共振的受迫振動，其動力學方程為

設阻尼項，激勵頻率以及系統(tǒng)的固有頻率均與ε同數量級，令

同樣將方程（24）的解設為式（3）的形式，與式（25）一起代入方程（24）中，再令F0=ω20B1，引入新的自變量ψ=ωt，令ε的同次冪項的系數相等，可以導出以下一系列的方程。

由方程（26）可以解出

將此解代入方程（27）中并整理得

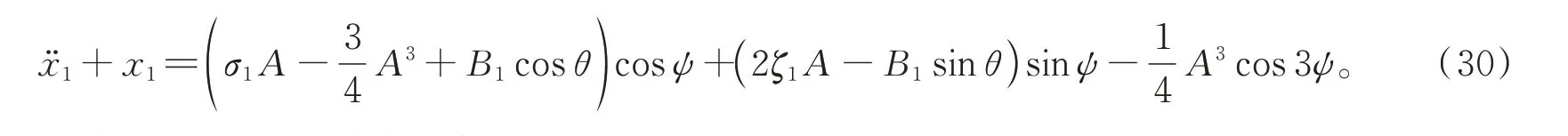
為消去共振對系統(tǒng)的影響，需要消除久期項，得到

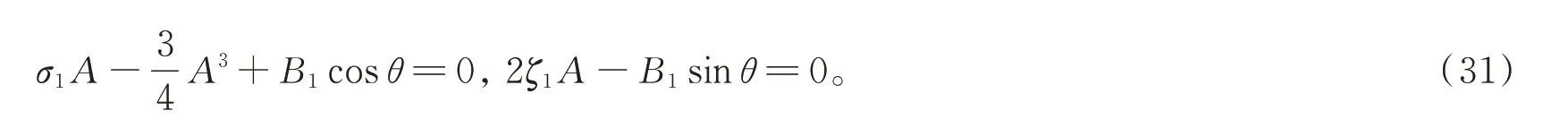
消去久期項后，可以設方程（30）的解為

把所設方程的解代入方程（30）中，可以解得

將式（32）與式（29）代入式（28）中得

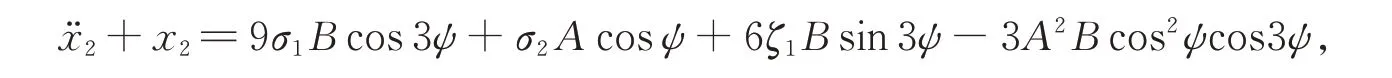
整理得

同樣地，消去久期項得

設方程（33）的解為

將式（34）代入方程（33），整理后得

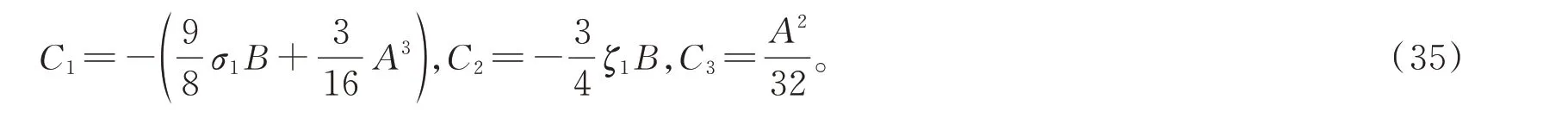
由此得

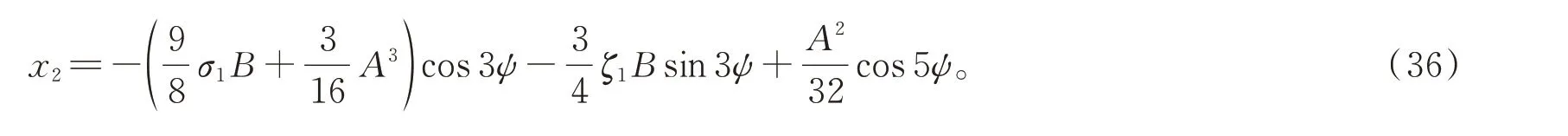
故而方程（24）的二階近似解便可給出

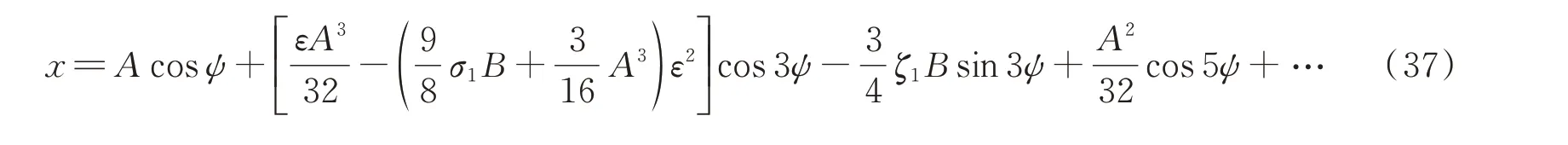
3 亞諧波共振

討論亞諧波共振的動力學方程

同樣設該方程的解為式（3）的形式，并令

將式（3）與式（39）同時代入方程（38）中，得到

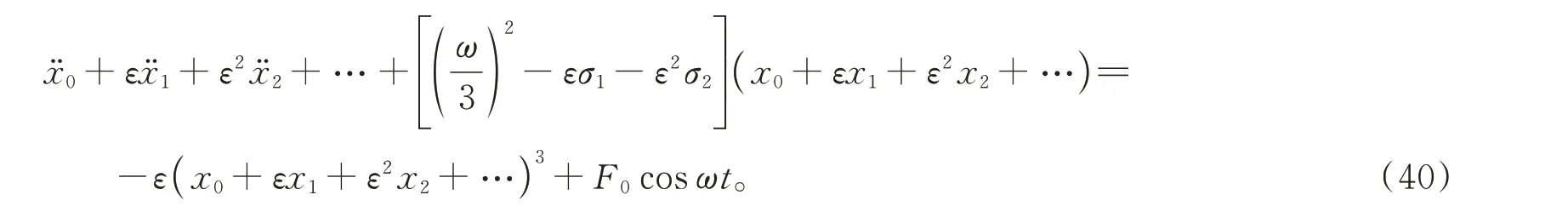
令上式中兩邊ε的同次冪項的系數分別相等，由此可以推導出一系列的方程。

設方程（41）解的形式為

其中，A13由初始條件決定，將式（44）代入方程（41）中得

將式（44）代入方程（42）中并整理得

為了消除方程中的久期項，得到

或

解出A13的不等于零的解

消去久期項后，設

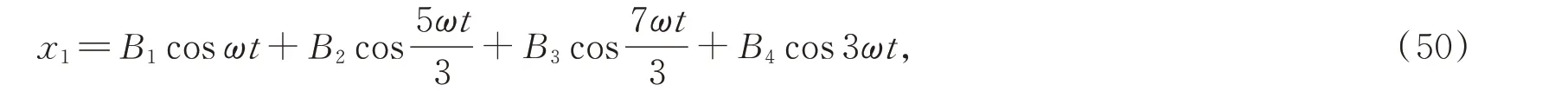
將式（50）代入式（46）中，可以得到

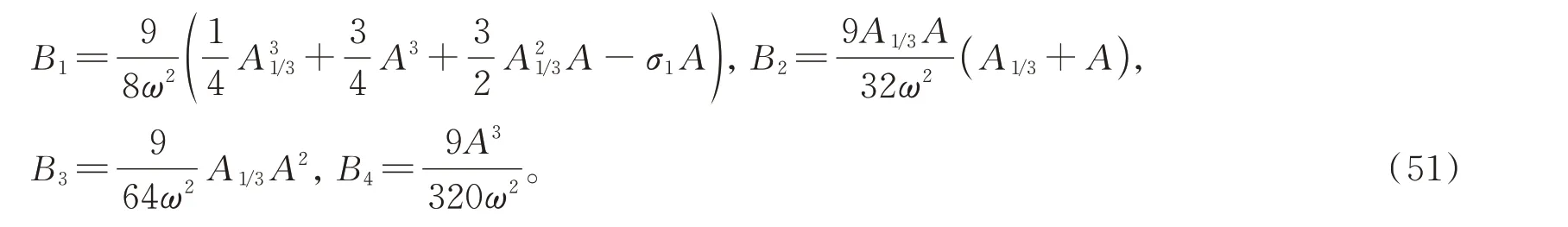
將式（50）和（44）代入方程（43）中，得到

整理后得到

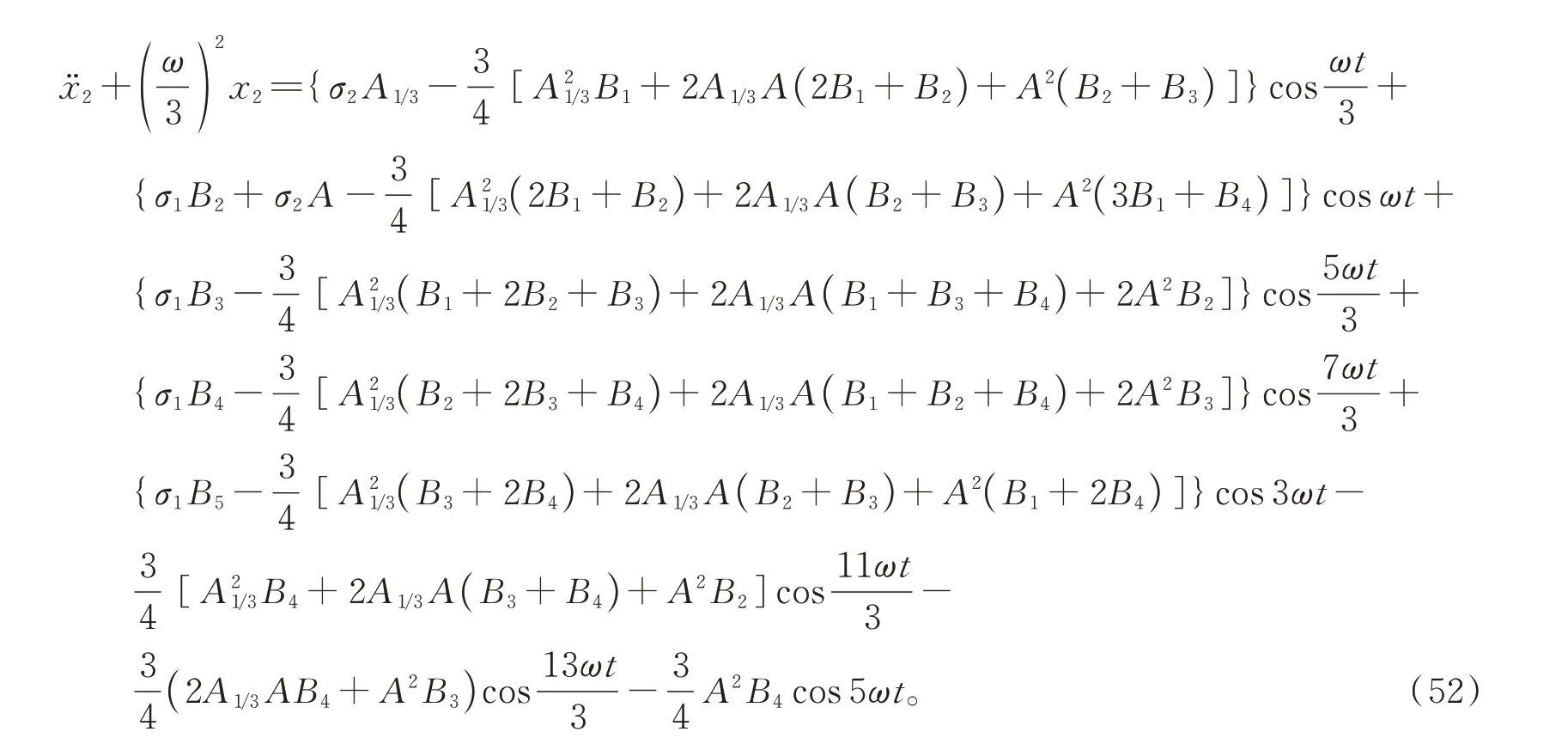
為了消除久期項，得

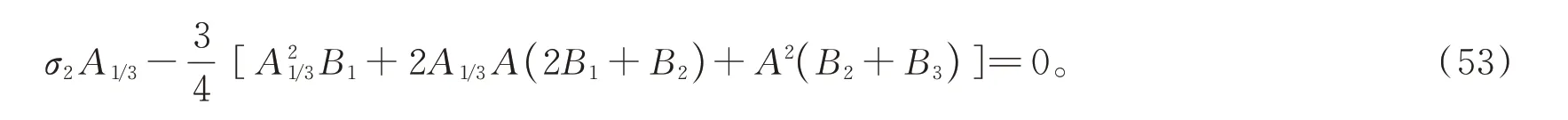
綜上，方程（38）的解可以寫成

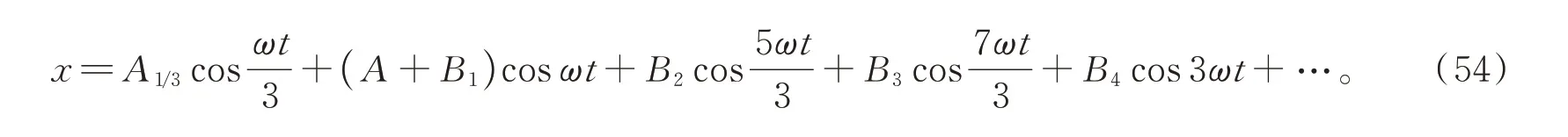
4 結論

林滋泰德為了消除天文學中的久期項改進正規(guī)攝動法，龐加萊為改進的攝動法的合理性進行了數學證明，林滋泰德-龐加萊法和正規(guī)攝動法同稱為小參數法，也叫PL攝動法。該方法的基本思想是認為非線性系統(tǒng)的固有頻率ω并不等于派生系統(tǒng)的固有頻率ω0，而應該是小參數ε的未知函數。因此在將基本解展成ε的冪級數的同時，因將頻率也寫成ε的冪級數，冪級數的待定系數根據周期運動的要求依次確定。本文以達芬系統(tǒng)的自由振動為例，利用林滋泰德-龐加萊法給出了三階精度的近似解析解，相比較文獻［1］從二階提高到了三階，進而提高了解的精確程度；討論了帶微弱阻尼的達芬系統(tǒng)接近共振的受迫振動，利用該方法給出了二階精度的近似解，比文獻［1］中的解提高了一階精度；針對亞諧波共振的情形，將文獻［1］中的解的精度由一階提高到了二階。利用林滋泰德-龐加萊法對達芬系統(tǒng)的三種不同振動的解求解，實現了非線性振動系統(tǒng)解的精度的提高，進而能夠更好地分析非線性系統(tǒng)的運動規(guī)律，以及對系統(tǒng)參數和初始條件的依賴關系。但是，得到非線性振動高階近似解，會增加很大的工作量，因此往往要截斷高階項只保留級數的前面有限項，同時解的最后結果還需要試驗來驗證。

小參數法是從事理論研究的重要數學工具之一，對于弱非線性問題尤其有作用。理論的研究從實際問題中來，并最終應用到實際問題中，小參數法在基礎和應用研究中已被廣泛應用于微分方程、軌道力學、非線性振動、固體力學、流體力學等領域［3-6］，并且隨著科學的不斷發(fā)展，一定會研究出更多有關小參數的理論，對它的應用也會更加廣泛。