非齊次樹上馬氏鏈基于韋伯分布的一個強偏差定理
任雙雙 蘭曉博
(鄭州科技學院基礎部 河南鄭州 450064)
近年來,許多學者對樹指標隨機過程的研究至今方興未艾,其中關于強偏差定理的研究也一直頗受青睞。文獻[1]主要研究并給出了馬氏環境中關于齊次樹指標的馬氏鏈的漸進均分性,文獻[2]研究并給出了樹指標馬氏鏈關于廣義幾何分布的一個強偏差定理,文獻[3]給出了關于樹指標非齊次馬氏鏈的廣義熵遍歷定理。該文通過引入滑動相對熵的概念,構造適當的tn(λ,ω),將Doob鞅收斂定理和上、下極限性質應用到定理中,研究并給出了關于韋伯分布的強偏差定理,使該方面的內容得到了擴充。
1 基本概念
定義1 定義{Xσ,σ∈T}是概率空間{Ω,F,P}上,且在連續狀態(R+,β(R+))取值的隨機變量族,設

是隨機變量族{Xσ,σ∈T}的初始分布,且正則條件概率族[4]記為
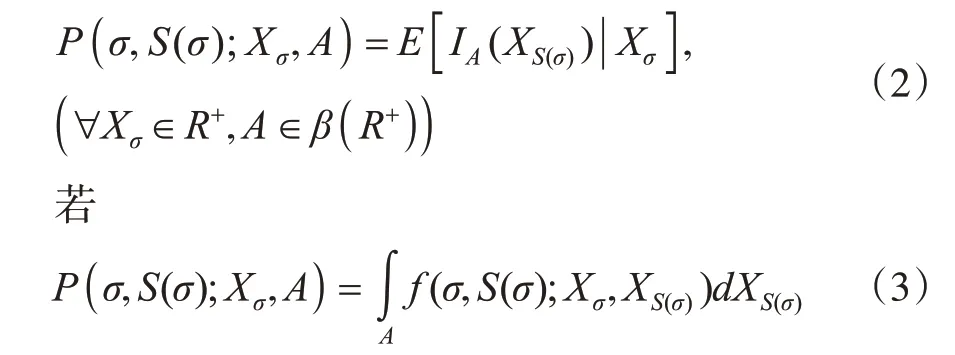
則稱f(σ,S(σ);Xσ,XS(σ))為轉移密度函數,記

定義fS(σ)(Xσ,XS(σ))是初始分布{Xσ,σ∈T}的一列轉移密度函數,將f0定義為{Xσ,σ∈T}對應的概率密度函數,于是稱為具有式(1)和式(2)的在R+上取值的連續狀態樹指標非齊次Markov鏈[5]。
則定義的樹T上聯合分布密度函數[6]為

設(Ω,F)上的另一概率測度為Q,{Xσ,σ∈T}在Q下的聯合分布密度函數記為

也就是{Xσ,σ∈T}在Q下互相獨立,并且服從的韋伯分布,其中,λξk>0,α>0,xξk∈R+,ξk∈Lk。
定義2{Xσ,σ∈T}在P和Q下的聯合分布密度函數均如上式所定義,設0 ≤a1≤a2≤…是一列整數值,分別記


定義3 設f(x)是隨機變量X的密度函數,如果存在0 <δ<1使
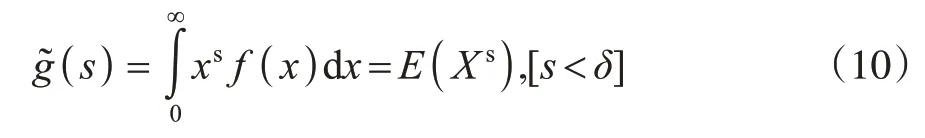
存在,則稱(s)是隨機變量X的s-矩變換。
由式(10)知,對于服從分布g(xξk,λξk)的隨機變量Xξk的s-矩變換為

2 強偏差性質
引理1 設{Xσ,σ∈T}為如上定義的連續狀態樹指標非齊次Markov 鏈,其中0 ≤a1≤a2≤…是一列整數值,s為一實數,f(X Tn),g(X Tn),(s,λξk)如前定義,令
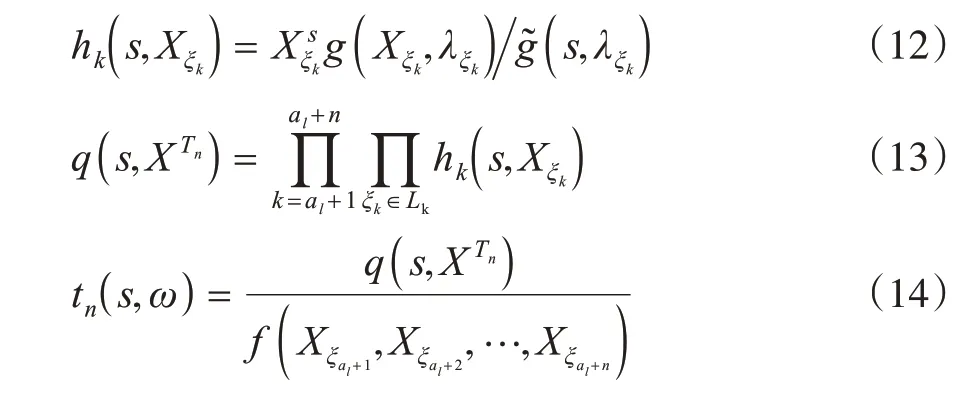
則{tn(s,ω),σ(Xξal+1,Xξal+2,…,Xξal+n),n≥1}在概率測度P下是一非負鞅。
證明由式(5),有
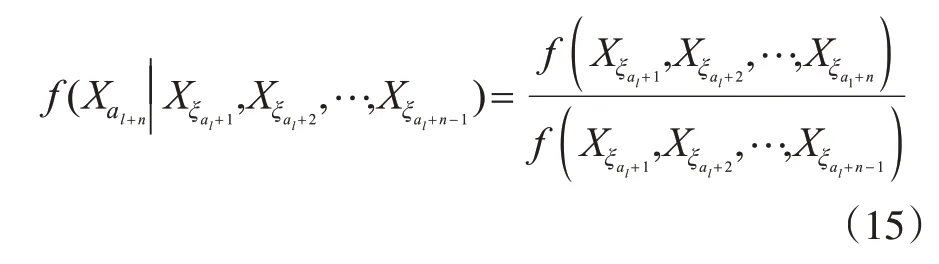
由式(11)、式(12)、式(13)與式(14),有
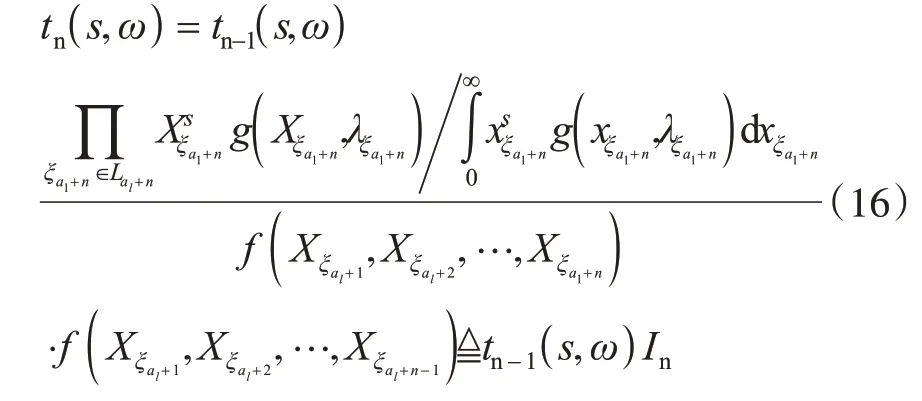
由式(15)與式(16),有
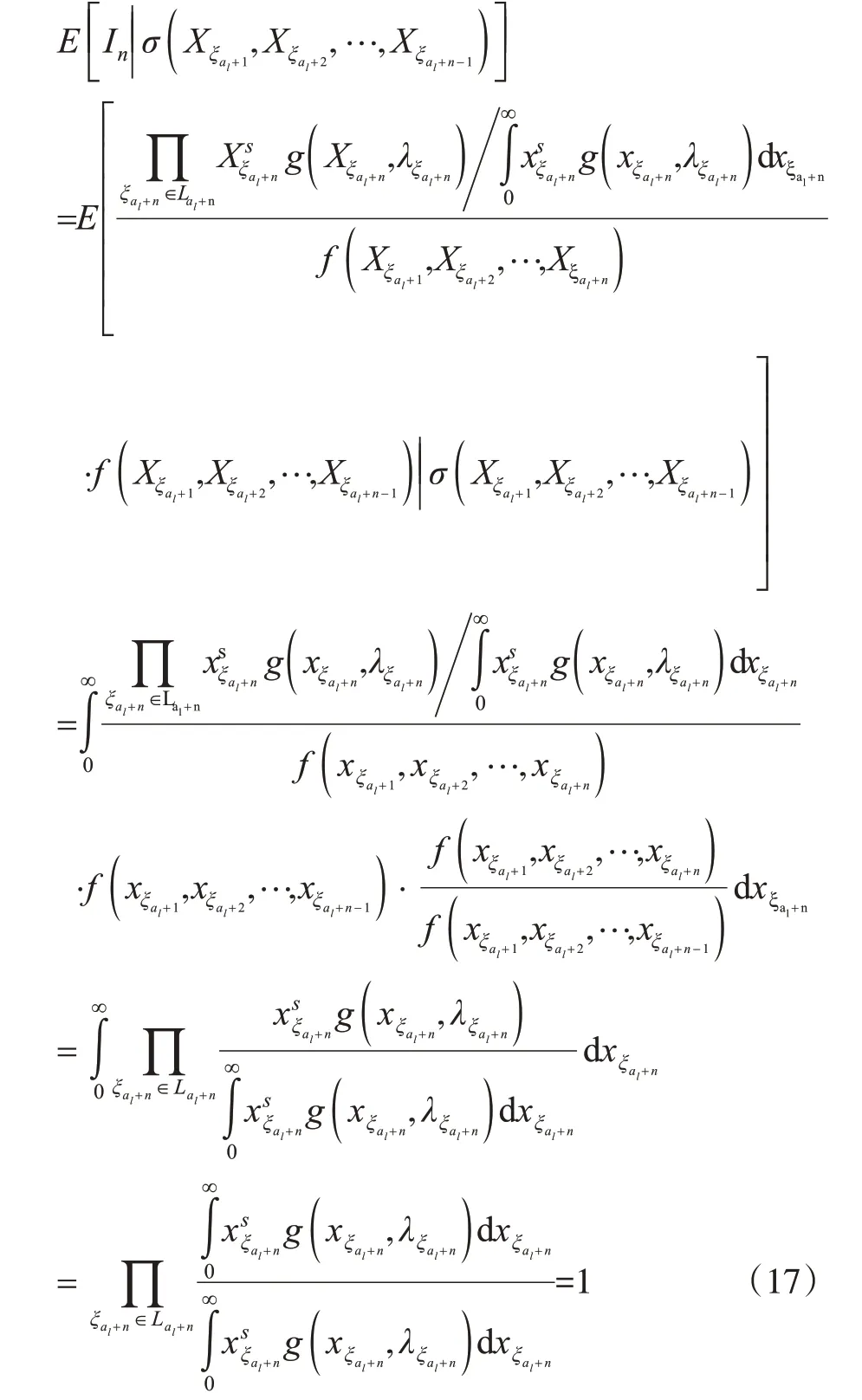
由(16)式和(17)式,有
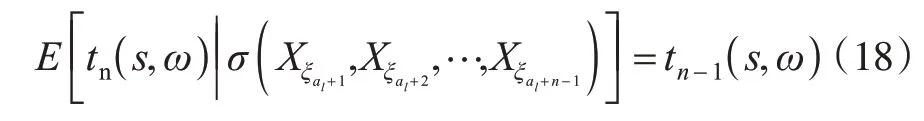
則{tn(s,ω),σ(Xξal+1,Xξal+2,…,Xξal+n),n≥1}在概率測度P下是一非負鞅[7]。
定理1 設{Xσ,σ∈T}為如上述定義的連續狀態樹指標非齊次Markov鏈,其在Q下的聯合分布密度函數如式(6)所定義,實數s∈(-1,1),正整值數列{al,l≥1}如前定義。設存在M>0,使得
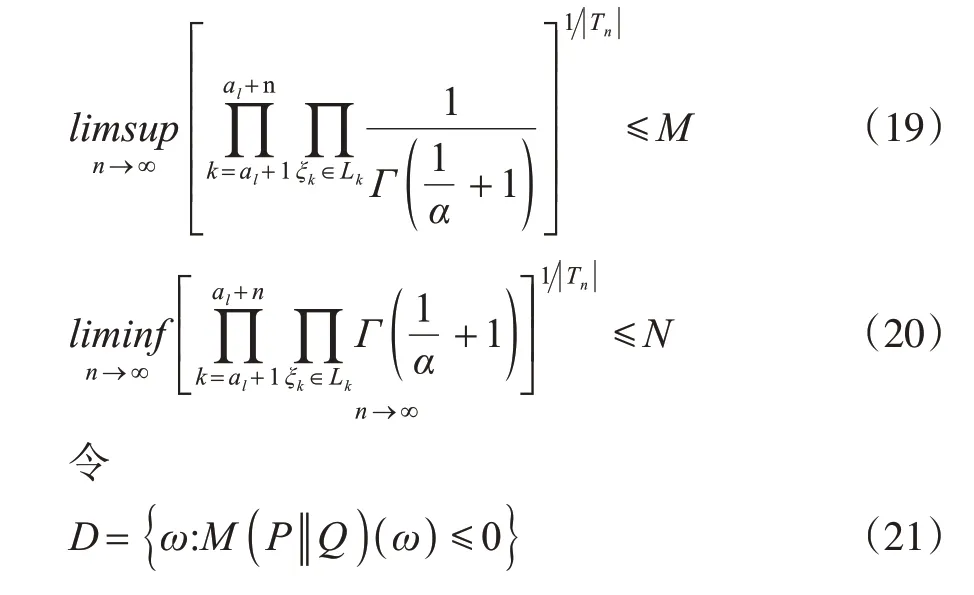

證明 由引理1 及Doob 鞅收斂定理[8]知,存在A(s) ∈F,P(A(s))=1,使得

由式(7)、式(11)、式(12)、式(13)與式(14),有

由(25)式,有

由式(8)、式(9)、式(21)、式(24)及式(26),有

取0 <s<1,將(27)式兩端同除以s,有


由不等式lnx≤x-1(x>0)及式(11)、式(19)、式(29)可知


由式(31),有式(22)成立。
取-1 <s<0,將式(27)兩端同除以s,有

由式(32)及下極限的性質
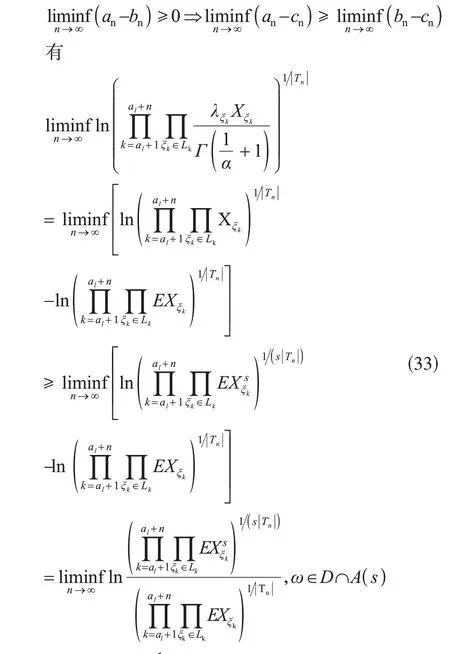


由式(35),有式(23)成立。

