地面和埋置爆炸土中地沖擊作用分區數值模擬及試驗研究*

劉 琦，翟超辰，張躍飛，曲建波，吳祥云

（1. 湘潭大學土木工程與力學學院，湖南 湘潭 411105；2. 軍事科學院國防工程研究院工程防護研究所，河南 洛陽 471023）

地表或淺埋爆炸產生的能量一方面用于破碎爆炸附近的巖土介質形成飛散的拋擲體，另一方面與地表上面的空氣發生相互作用，在空氣中形成沖擊波。爆炸時，通過直接壓縮地介質并在其中形成的波稱為直接地沖擊，而空氣中的沖擊波掠過地表，通過壓縮空氣和地介質相互作用形成的在地介質中傳播的波稱為感生地沖擊。所以爆心附近土中淺層地下介質所受地沖擊荷載比較復雜，既有直接地沖擊，也有感生地沖擊。地沖擊和空氣沖擊波到達地表觀測點的時間相對關系由巖土介質中的地沖擊傳播速度和空氣沖擊波傳播速度差異決定，不同介質、不同埋置深度的爆炸造成地沖擊應力、加速度場的不同分布。

近年來，對于巖土介質中直接地沖擊方面的研究已經較為完善。Wu 等通過現場大型地下爆炸試驗，研究了介質內部、巖土界面和地表的爆炸應力波特性；給出并分析了實測應力波時程及其特征參數，如質點速度峰值和質點加速度峰值以及不同位置的主頻率。何翔等通過石灰巖中不同裝藥深度的爆炸試驗，得到了石灰巖中爆炸成坑經驗公式以及地沖擊傳播規律。Leong 等根據新加坡殘積土的小規模現場爆破試驗，檢驗了TM5-855-1 對應力峰值的估算。吳祥云等通過現場試驗研究了常規裝藥爆炸埋深對自由場直接地沖擊參數的影響，得到了不同巖土介質、不同地沖擊參數等效當量埋深系數的計算方法。葉亞齊等運用等效當量埋深系數，給出了砂質黏土中不同深度爆炸自由場地沖擊參數的預估方法。Yankelevsky 等通過現有經驗數據的分析和數值模擬，研究了土中爆炸沖擊波峰值壓力衰減特性。Jayasinghe 等對不同埋深爆炸條件下飽和砂土中樁的動力響應進行了數值分析，給出了爆炸波在土體中的傳播和樁的水平變形。Song 等對聚能裝藥爆炸過程進行了數值模擬，得到了土介質的動力響應、爆炸空腔的形成和發展規律以及爆炸波在土中的傳播規律。

然而，感生地沖擊方面的研究則十分有限，且大多是研究觸地爆炸條件下的感生地沖擊效應。埋置爆炸條件下土中感生地沖擊的影響范圍尚不明確。Alekseenko 等基于相似理論進行了相關試驗研究，試驗測量結果如圖1 所示，得到了土中壓縮波的大致分布情況以及表面區域地沖擊有2 個峰值等結論。Beshara基于擬靜態特性，給出了包括烈性炸藥、混合氣體和粉塵懸浮物在內的多種內爆氣體壓力的半經驗關系式和預測方法，在忽略土-結構相互作用的情況下，給出了一種感生地沖擊和直接地沖擊的簡化計算形式。Wu 等基于對地面爆炸的一系列參數化數值模擬，確定了可以應用于結構響應分析的地沖擊和空氣沖擊波荷載。然后，他們以單層砌體填充的鋼筋混凝土框架為例，計算了結構在地沖擊和空氣沖擊波共同作用下，或單獨在地沖擊和空氣沖擊波作用下的動力響應和損傷。范俊余等結合Alekseenko 等的試驗現象，對炸藥地面爆炸條件下淺地表波場的分布以及作用到土中淺埋結構上的荷載進行了數值模擬研究，發現典型土中淺埋結構的頂板主要承受感生地沖擊的作用，外墻主要承受直接地沖擊的作用。柳錦春等基于數值模擬結果和試驗數據，對根據一維平面波理論和特征線解法得到的空氣沖擊波為突加三角形荷載的感生地沖擊的理論計算公式進行修正，提出了炸藥地面接觸爆炸下土中感生地沖擊的實用計算方法。楊仁華等采用平面裝藥方法進行了核彈空爆試驗模擬研究，給出了間接地沖擊在黃土中的衰減規律。吳祥云等通過石灰巖中不同裝藥深度的爆炸試驗，研究了石灰巖中裝藥埋深對地表空氣沖擊波超壓的影響，給出了不同埋深爆炸地表空氣沖擊波超壓峰值的預計方法。Krauthammer 等和Chee基于高能炸藥模擬技術（high explosive simulation technique，HEST）試驗，提出了一種改進的單自由度（single-degree-of-freedom，SDOF）方法，并對淺埋鋼筋混凝土箱形結構在空氣沖擊波荷載下的受力性能進行了一系列研究。榮吉利等提出了考慮感生沖擊波與直接沖擊波疊加效應的核爆地沖擊描述方法，并以美軍核爆地沖擊試驗為例研究了核爆地沖擊作用下土體運動特性。

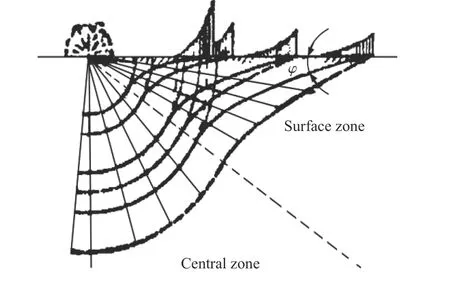
圖1 波陣面的連續位置[9]Fig. 1 Successive locations of wave fronts[9]

為了研究爆炸條件下土中直接地沖擊和感生地沖擊的影響范圍，本文中利用ANSYS/AUTODYN 軟件建立二維軸對稱有限元模型，開展土中爆炸地沖擊效應數值模擬分析；通過黃土中爆炸試驗，測得不同比例爆距上地面空氣沖擊波超壓和土中直接地沖擊豎向應力，并以此進行計算模型的驗證；利用驗證后的計算模型，對裝藥不同比例埋深和不同類型炸藥的土中爆炸進行數值模擬；根據不同工況的計算結果，獲得不同爆炸條件下土中感生地沖擊和直接地沖擊荷載的作用特征，并以此對地沖擊作用區域進行劃分；最后分析影響地沖擊作用區的關鍵參數。

1 計算模型

1.1 幾何模型

建立了如圖2 所示的模型，該模型由炸藥、空氣和黃土3 部分組成，其中，對炸藥和空氣采用歐拉算法，對黃土采用拉格朗日算法。數值模擬中采用ANSYS/AUTODYN 軟件的自動流固耦合算法。炸藥裝藥為圓柱體，起爆點為炸藥的幾何中心。

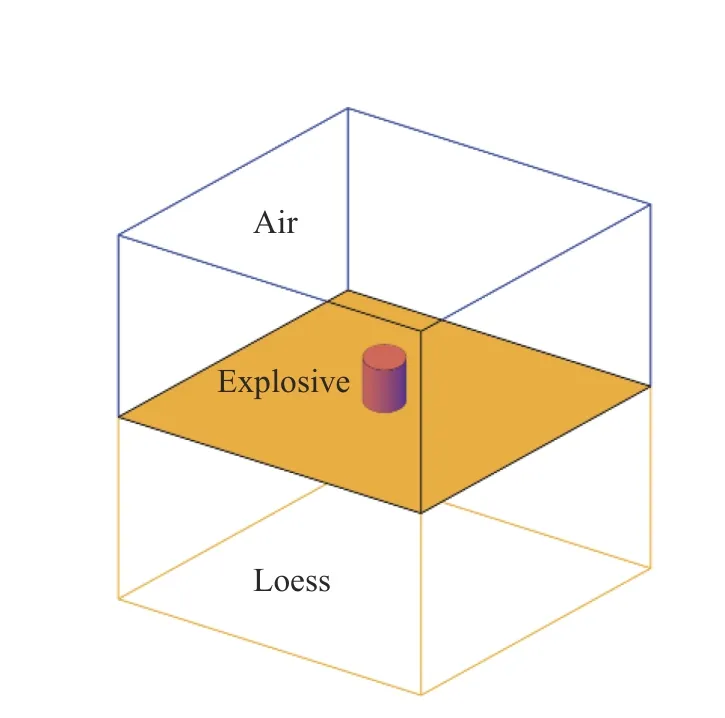
圖2 爆炸模型Fig. 2 The explosion model

計算工況如表1 所示。B1～B10 為TNT 炸藥不同比例埋深的工況，裝藥量為1 kg，比例埋深分別為-0.05、-0.025、0、0.025、0.05、0.075、0.1、0.2、0.3 和0.4 m/kg。C1～C12 為不同類型炸藥的工況，不同工況以炸藥的初始比內能為依據進行等效處理。炸藥類型分別為ANFO、C4、EXPLOS.D、HMX、HNS 1.65、NM、PBX9407、PBX9502、PETN 1.77、SEISMOPLAS、TETRYL、TNT。

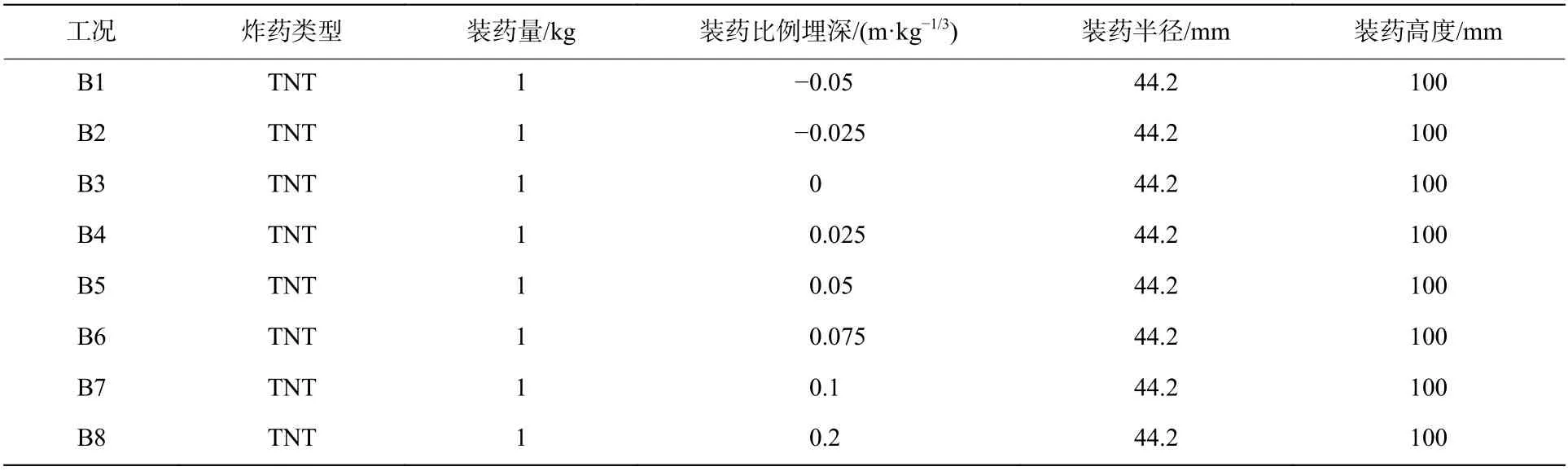
表1 計算工況Table 1 Calculation conditions

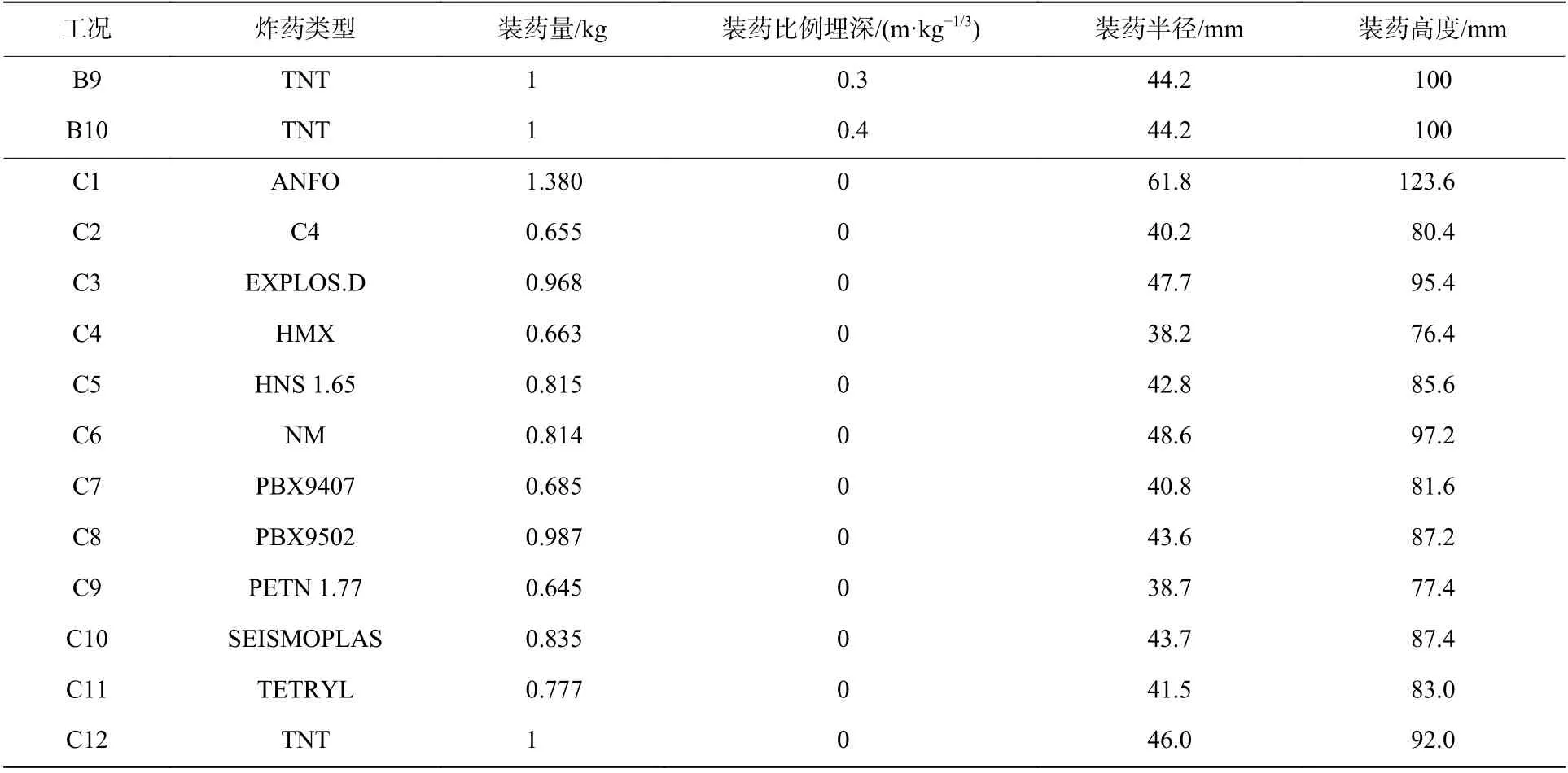
表1（續）Table 1 (Continued)

1.2 有限元模型

考慮到計算模型的對稱性，建立了二維軸對稱有限元模型，計算域尺寸為4 m×8 m，如圖3(a)所示。其中，空氣尺寸為4 m×8 m，炸藥通過Fill 命令填充在空氣中。如圖3(b)所示，歐拉域的左邊界為對稱邊界，其他3 條邊界為流出邊界。如圖3(c)所示，拉格朗日域的左邊界為對稱邊界，下邊界和右邊界為傳輸邊界，其余邊界為自由邊界。

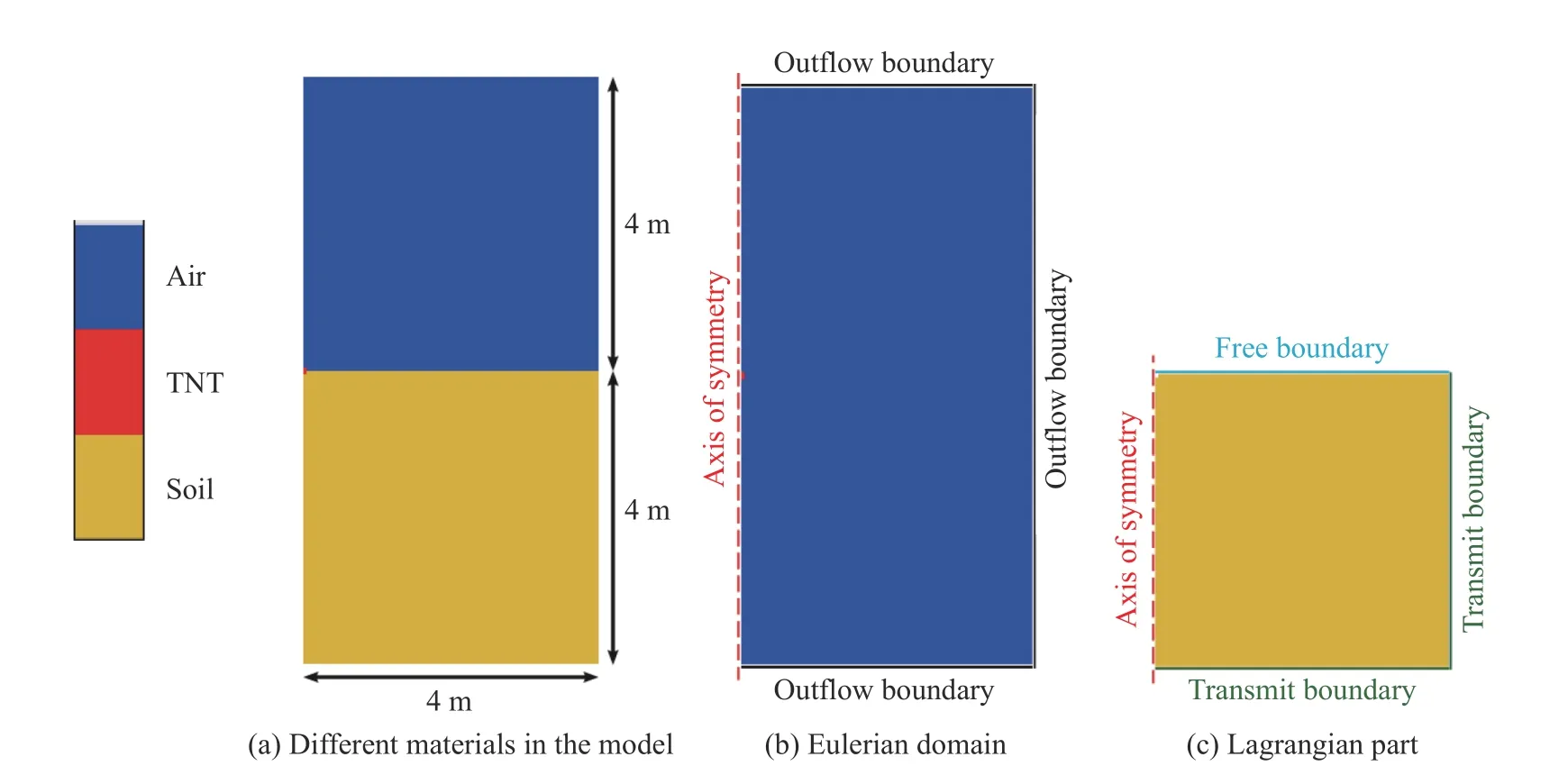
圖3 有限元模型和邊界條件Fig. 3 The finite element model and boundary conditions

如表1 所示，對于計算工況B1～B10，炸藥尺寸為 ? 88.4 mm×100 mm。黃土的寬度為4 m，隨裝藥比例埋深的增大，黃土的高度略有差別。炸藥附近區域的局部放大如圖4 所示，炸藥放置位置以上為空氣，以此模擬鉆地武器的鉆地效果。對于計算工況C1～C12，炸藥密度和裝藥量的不同導致裝藥尺寸略有差別，黃土的寬度為4 m，高度為4 m。

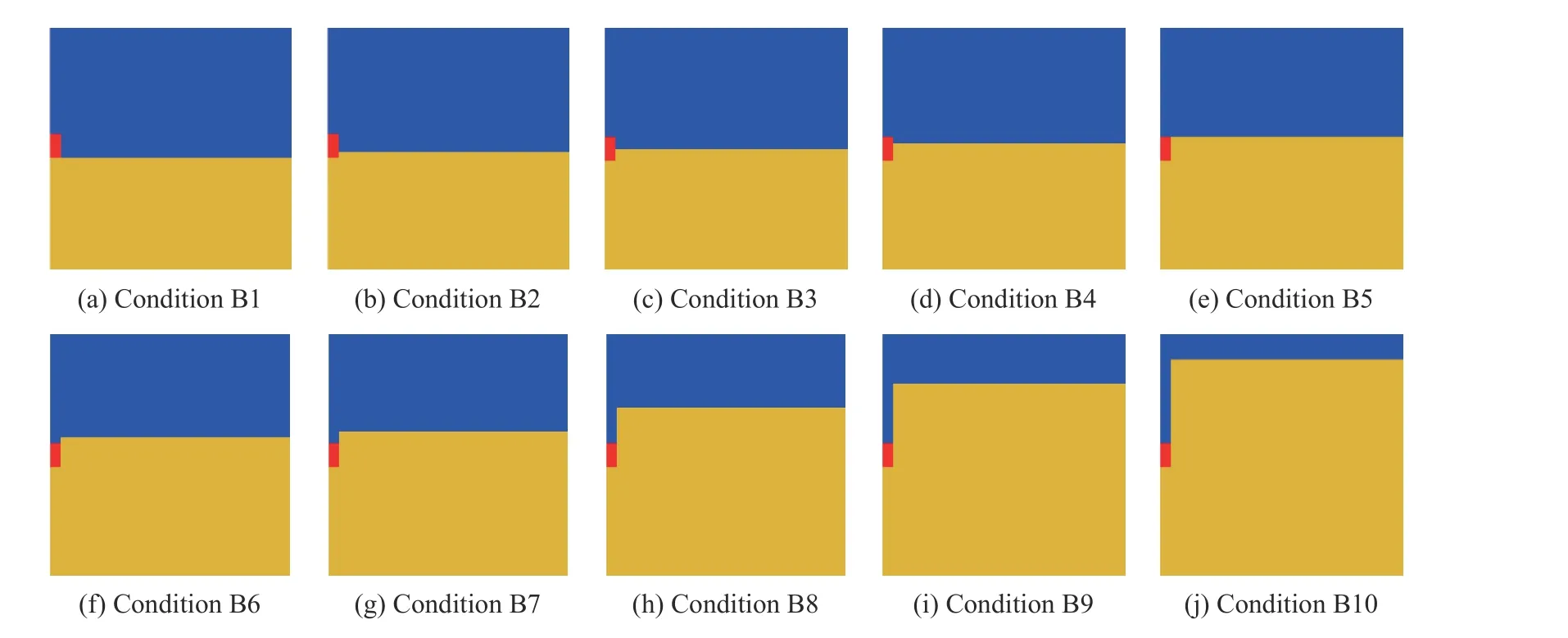
圖4 工況B1～B10 下炸藥附近區域的放大Fig. 4 Enlarged details near TNT under conditions B1-B10

以工況B3 為例，圖5 給出了有限元模型的網格劃分情況。炸藥網格的徑向長度為4.42 mm，高度方向長度為5 mm。對空氣和黃土以炸藥網格的尺寸為基礎采用漸變網格，空氣網格的最小尺寸為4.42 mm×5.0 mm，黃土網格的最小尺寸為8.84 mm×10.0 mm。整個有限元模型中，歐拉單元為165 000個，拉格朗日單元為36 000 個，共201 000 個單元。

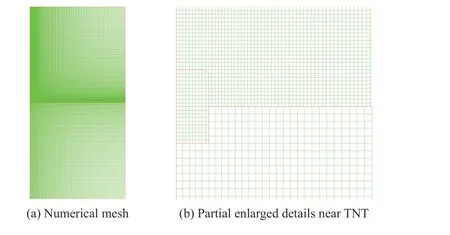
圖5 數值網格Fig. 5 Numerical mesh

1.3 材料模型

1.3.1 炸藥

炸藥采用ANSYS/AUTODYN 內置材料庫中的炸藥模型。Jones-Wilkins-Lee （JWL）狀態方程常用來描述炸藥的爆炸和膨脹，其表達式如下：

式中：γ 為理想氣體等熵絕熱指數，ρ 為氣體密度，為初始比內能。本文中空氣的初始密度為1.225 kg/m，γ=1.4，=206.8 J/g，比熱容為717.6 J/(kg·K)，參考溫度為288.2 K，這些參數均取自文獻[25]。

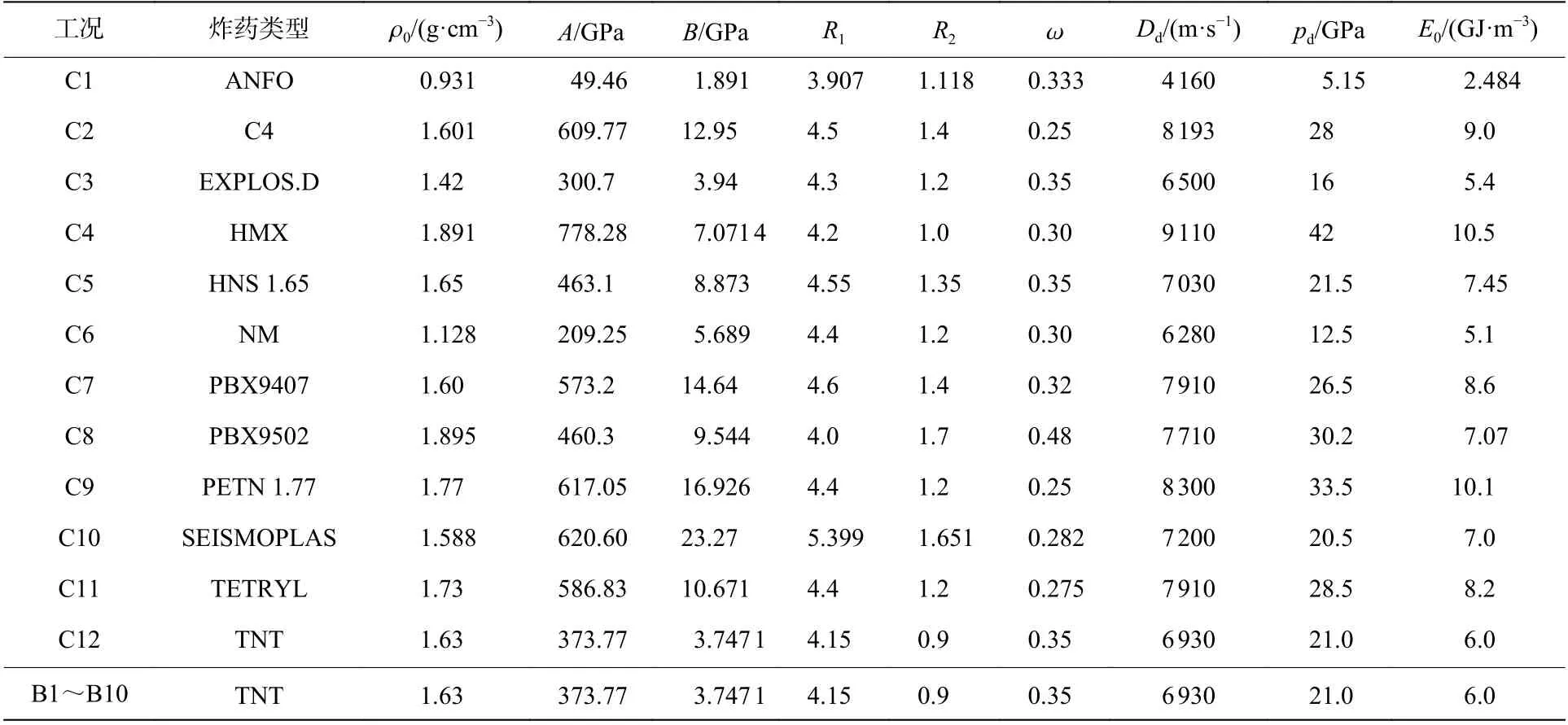
表2 炸藥參數[23]Table 2 Explosive parameters[23]

1.3.3 黃土

對黃土采用ANSYS/AUTODYN 軟件內置材料庫中的SAND 模型。Laine 等根據砂土在動態加載條件下的響應提出了SAND 模型，并基于該模型進行了一系列數值模擬研究。SAND 模型主要包括狀態方程與顆粒強度模型2 個部分。ANSYS/AUTODYN 軟件中的壓實態狀態方程分為線性和非線性2 類，SAND 模型選用的是線性壓實態狀態方程。壓實態狀態方程還可以與多種強度模型、失效模型共同描述材料的力學行為。顆粒強度模型是Drucker-Prager 強度模型的拓展，考慮了包括粉末、黏土和砂土等顆粒介質的強度。除了壓力強化效應，SAND 模型還描述了密度強化效應以及剪切模量與密度之間的函數關系。表3 為SAND 模型輸入的參數值。

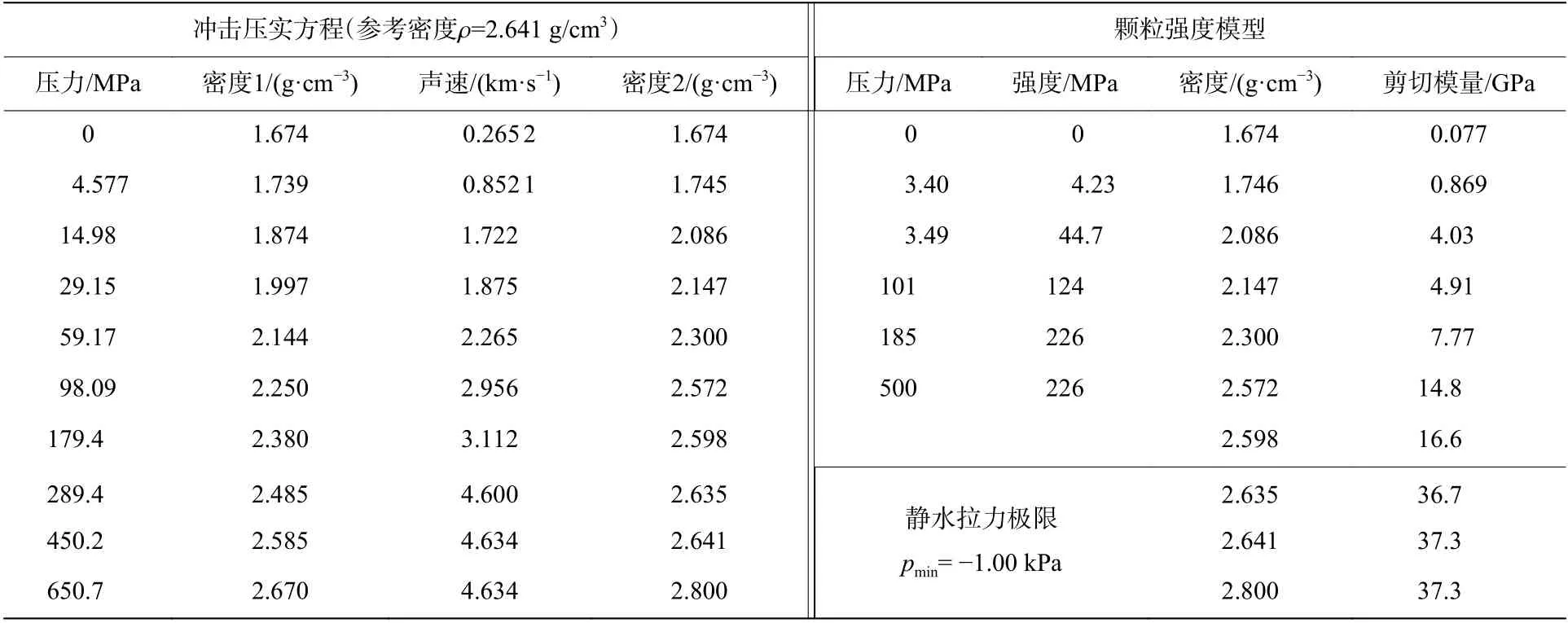
表3 SAND 模型參數[32-33]Table 3 Parameters of the SAND model[32-33]

試驗時，土介質為洛陽地區的黃土，該黃土比重為2.54～2.84，干密度為1 200～1 790 kg/m，天然含水率為10%～15%，黏聚力為30～60 kPa，內摩擦角為15°～25°。洛陽地區黃土的壓力（Pa）與體積應變 ε 的 關 系為：

因此，基于式(3) 對SAND 模型中沖擊壓實方程的壓力與密度1 的對應關系進行修正，如表4所示。

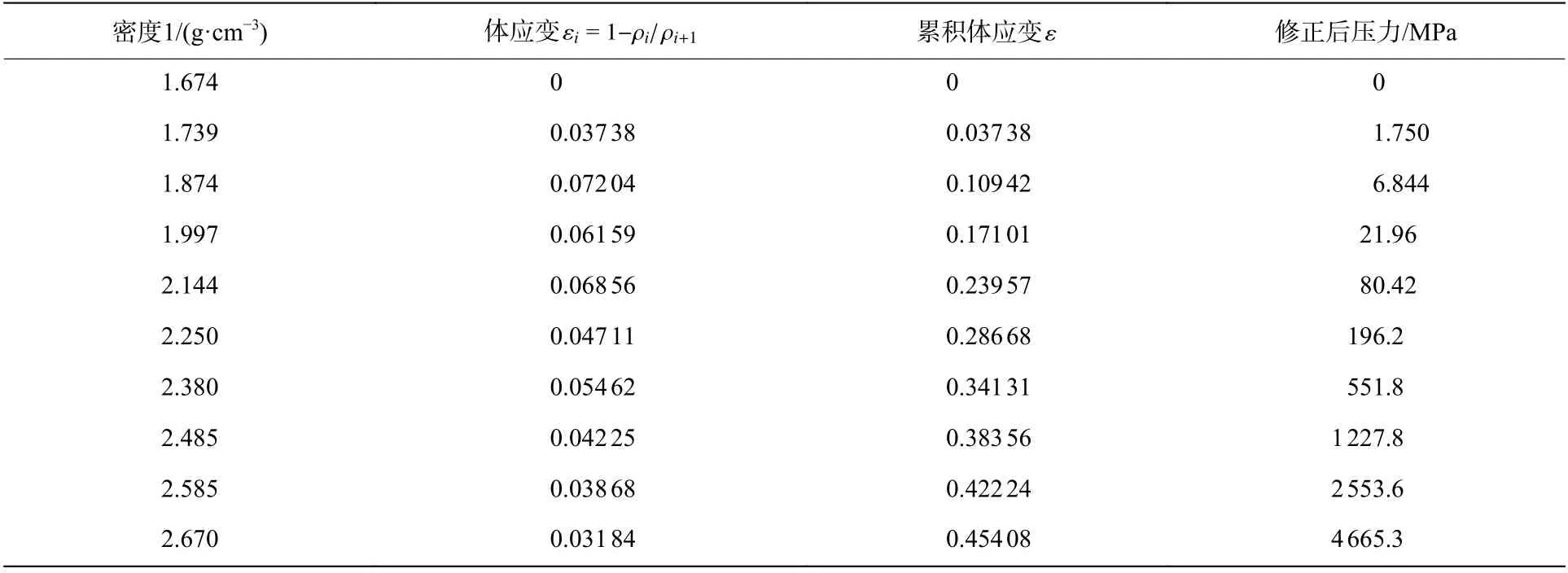
表4 線性壓實狀態方程中壓力與密度1 的關系（基于式(3)）Table 4 Relationship between pressure and density 1 in the compaction linear equation of state(based on formula (3))

2 計算模型的試驗驗證

2.1 試驗概況

圖6 為土中接觸爆炸和半埋爆炸的布置圖，TNT 炸藥的比例埋深分別為-0.05 和0.0 m/kg。地面布置空氣沖擊波超壓測點A1～A4，土中爆心正下方布置直接地沖擊豎向應力測點S1～S4。

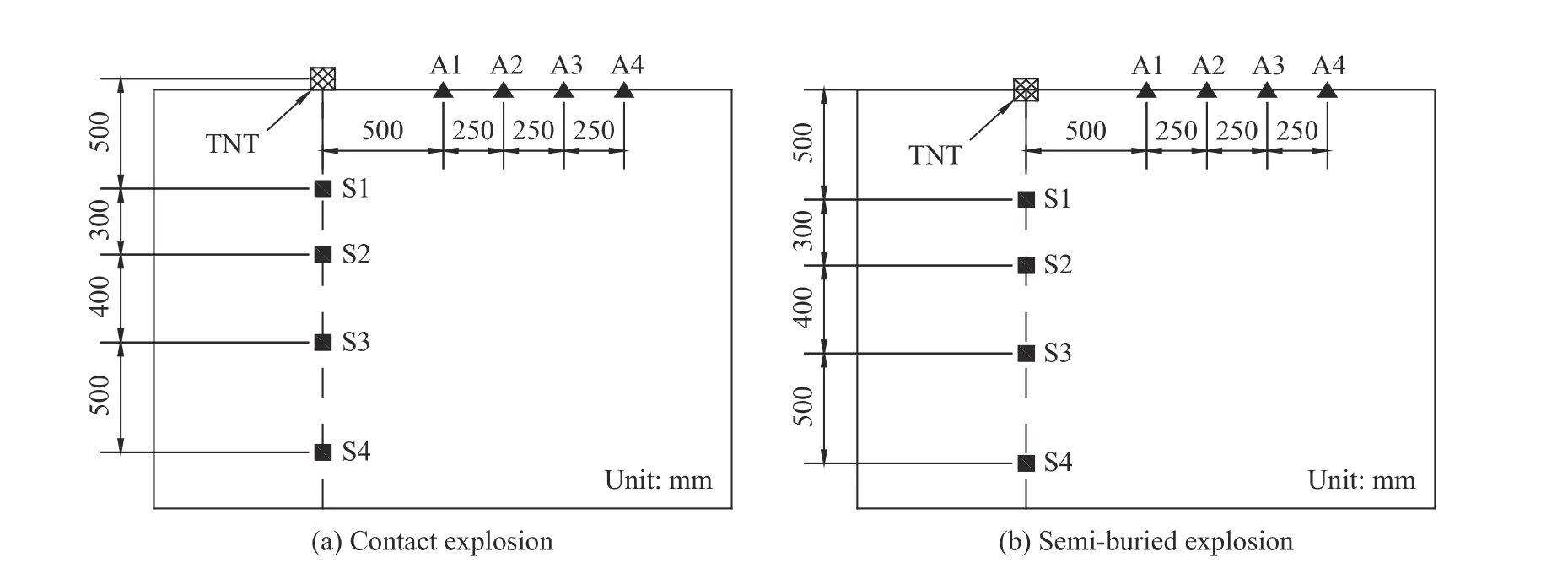
圖6 測試布置Fig. 6 Test arrangements

試驗中采用PCB 壓力傳感器（見圖7(a)）測試地面空氣沖擊波超壓，采用電荷式壓力傳感器（見圖7(b)）測試土中應力。圖6 給出了8 個傳感器的位置，4 個地面空氣沖擊波超壓測點距爆心水平距離分別為0.50、0.75、1.00 和1.25 m，4 個土中直接地沖擊豎向應力測點的爆心距分別為0.5、0.8、1.2 和1.7 m。回填黃土的密度控制在1 600～1 700 kg/m范圍內。數據采集儀選用了東華測試公司生產的DH5960 超動態信號測試分析儀（見圖7(c)），采樣頻率高達1 MHz。

圖7 試驗中的測量儀器Fig. 7 Measuring instrumentation used in test

2.2 試驗方案

試驗共進行2 炮次，工況見表5，試驗工況E1 和E2 分別對應數值模擬中的工況B1 和B3。圖8 為試驗準備完成后的現場布置。炸藥采用電雷管起爆，將電雷管插入炸藥中間，使得起爆點接近炸藥中心位置。

表5 試驗工況Table 5 Test conditions

圖8 試驗前現場布置Fig. 8 Site layout before the test

2.3 試驗結果與計算模型驗證

圖9 為試驗后的破壞情況。將坑底回落的土進行清理后，測得試驗E1 的真實爆坑直徑約為69.0 cm，真實爆坑深度約為23.5 cm；試驗E2 的真實爆坑直徑約為87.0 cm，真實爆坑深度約為27.5 cm。根據圖9 中傳感器的位置判斷，試驗E1 的爆坑唇緣直徑約為140 cm，試驗E2 的爆坑唇緣直徑約為160 cm。

圖9 試驗后破壞情況Fig. 9 Damages after the tests

采用截止頻率為2 000 Hz 的低通濾波方法處理試驗數據，這2 次試驗中各測點的時程曲線如圖10 所示，由于數據異常，部分測點未給出曲線。對比這2 次試驗數據，隨著裝藥比例埋深的增大，地面空氣沖擊波超壓峰值減小，而土中直接地沖擊應力峰值增大。圖10～12 和表6 給出了試驗與數值模擬結果的荷載峰值對比情況。其中，圖10 測得的地下應力，在不同距離的傳感器上測得波形在相同的時間均出現1 個類似的負向跳動，這是由于試驗時傳感器距離爆心較近，受到爆炸產生的電磁干擾。經計算，試驗數據與數值模擬結果的平均偏差約為14.8%。由此表明，試驗與模擬結果的一致性較好，可利用該計算模型做進一步分析研究。

表6 試驗與數值模擬荷載峰值Table 6 Peak loads obtained by tests and simulations

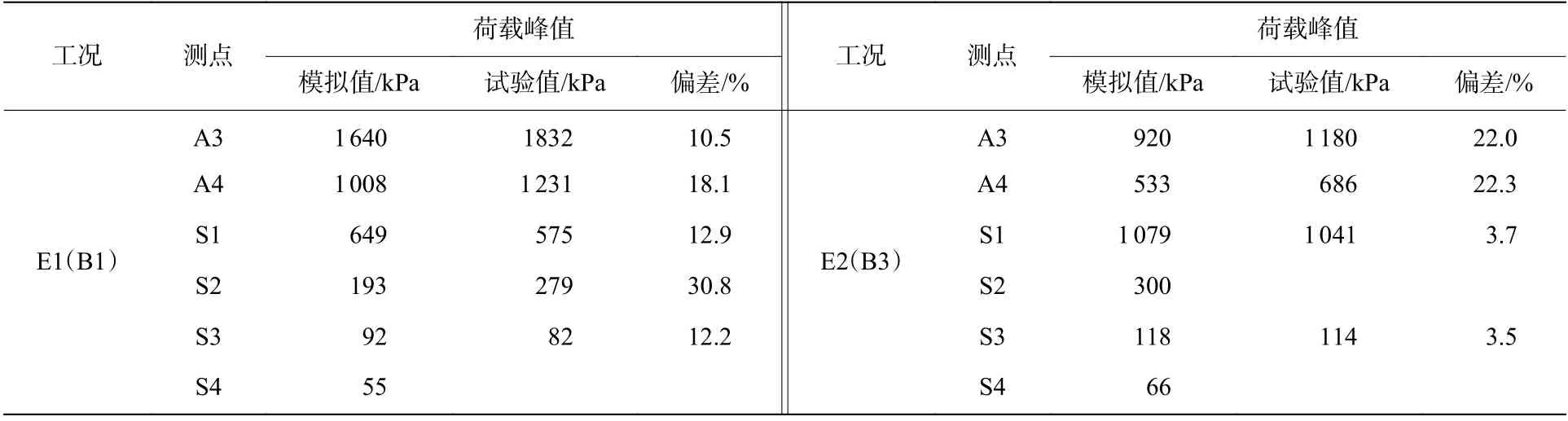
表6（續）Table 6 (Continued)

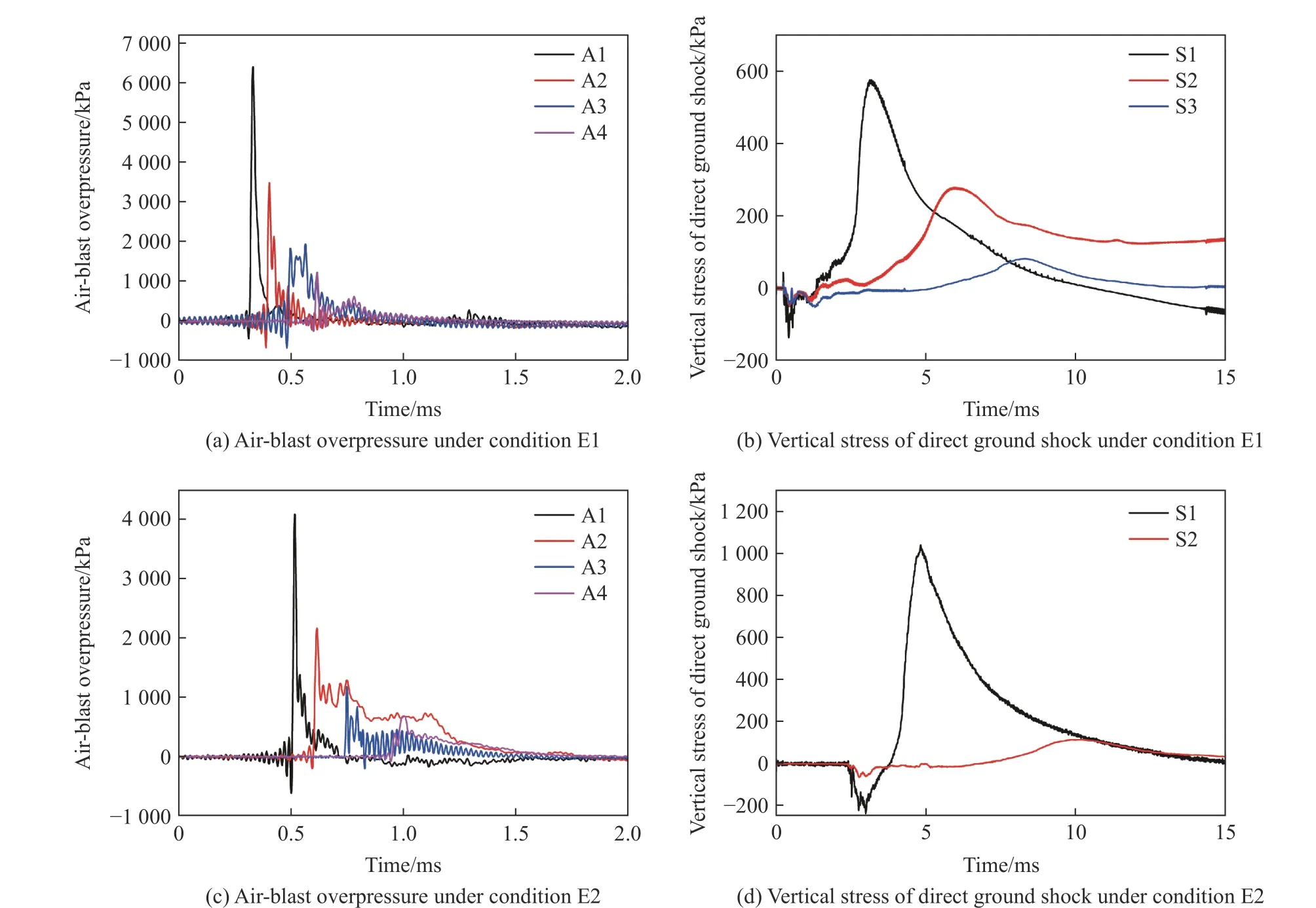
圖10 地面空氣沖擊波超壓和土中直接地沖擊豎向應力時程曲線試驗結果Fig. 10 Tested time history curves of air-blast overpressure and vertical stress of direct ground shock

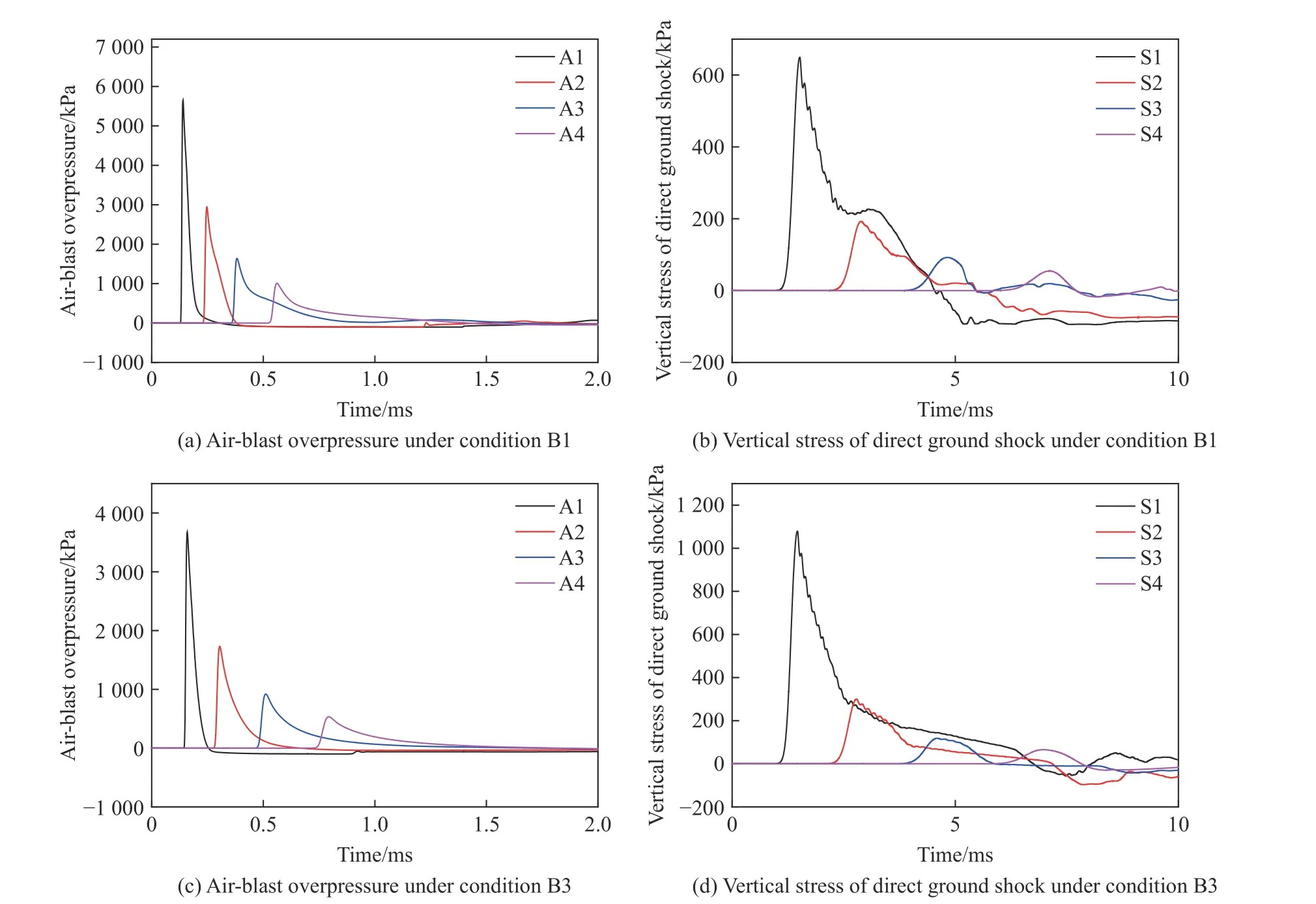
圖11 地面空氣沖擊波超壓和土中直接地沖擊豎向應力時程曲線數值模擬結果Fig. 11 Numerically-simulated time history curves of air-blast overpressure and vertical stress of direct ground shock

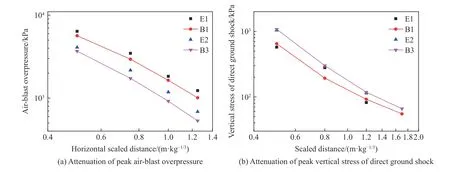
圖12 試驗與數值模擬數據對比Fig. 12 Comparison of tests and simulations

3 地沖擊作用分區

3.1 感生地沖擊影響范圍

基于已驗證的計算模型，對土中爆炸地沖擊效應作進一步數值模擬研究。以工況B3 為例，其壓力云圖如圖13 所示，從圖中發現土中應力波的時空分布與圖1相符，可將地沖擊作用區域劃分為表面區（即區域A 和B）和中心區（區域C）。

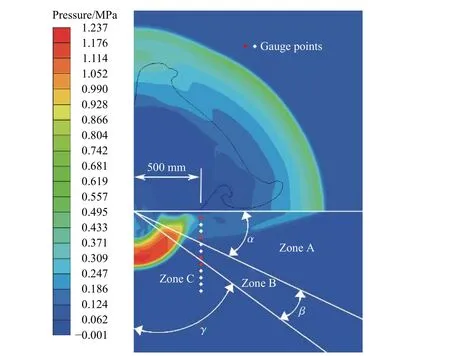
圖13 工況B3 下的壓力云圖Fig. 13 Pressure contours under condition B3

圖14(a)為表面區中地下5 cm 處壓力時程曲線，該時程曲線存在2 個明顯的峰值（即感生地沖擊峰值和直接地沖擊峰值）。圖14(b)為中心區中地下40 cm 處壓力時程曲線，該時程曲線只存在1 個峰值（即直接地沖擊峰值）。由地下5 cm 至地下40 cm 處的壓力時程曲線從2 個峰值減少為1 個峰值，表明隨著深度的增加，地沖擊作用區域的受力特征從感生地沖擊與直接地沖擊共同作用演變為主要受直接地沖擊作用。進一步分析表面區的受力特征，如圖15(a)所示，在區域A 中地下20 cm 處的豎向應力時程曲線存在2 個峰值，且感生地沖擊應力峰值明顯大于直接地沖擊應力峰值，此時感生地沖擊起主導作用。隨著深度增加，在區域B 中地下35 cm 處的豎向應力時程曲線如圖15(b)所示，此時同樣存在2 個峰值，但感生地沖擊應力峰值與直接地沖擊應力峰值相當，說明該區域受感生地沖擊和直接地沖擊聯合作用。根據表面區中不同深度豎向應力的特征，將表面區劃分為地表區（區域A）和近地表區（區域B）。圖14 和圖15 中地下測點具體位置在圖13 中用紅色點進行標注。

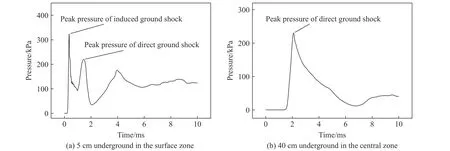
圖14 工況B3 下爆心水平距離0.5 m 處的壓力時程曲線Fig. 14 Pressure-time curves at the horizontal distance of 0.5 m from the detonation point under condition B3

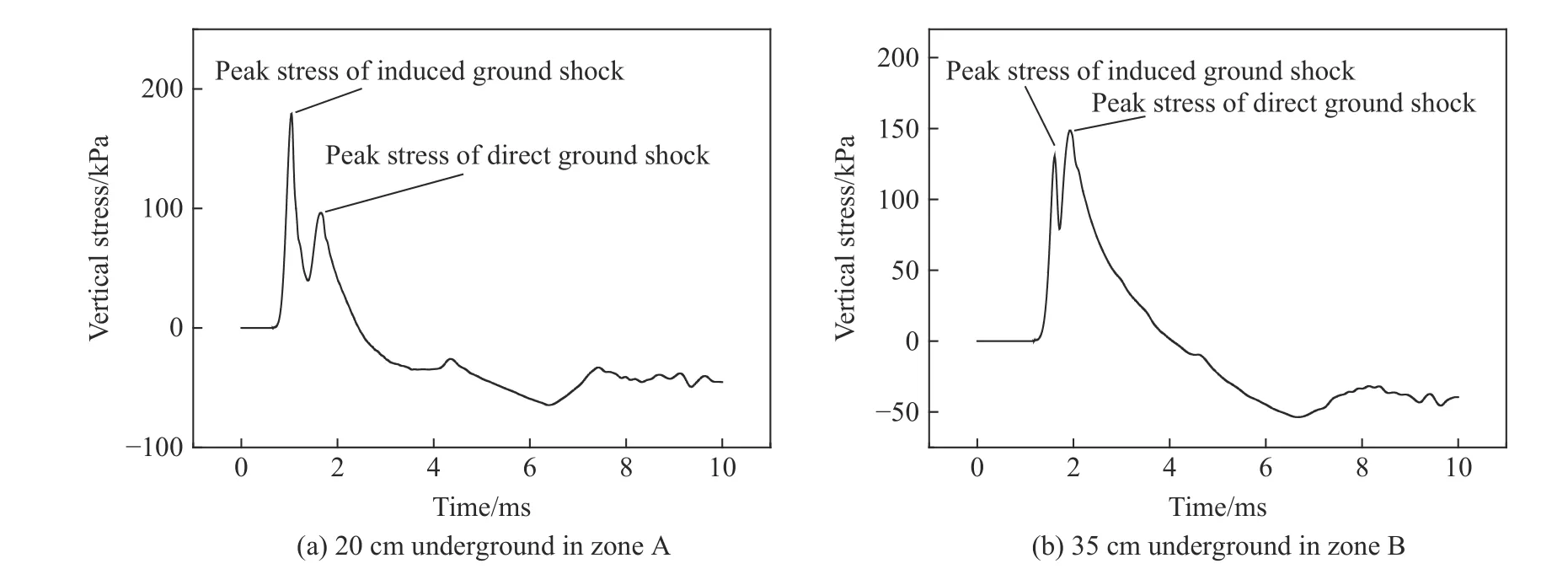
圖15 工況B3 下爆心水平距離0.5 m 處豎向應力時程曲線Fig. 15 Vertical stress time curves at the horizontal distance of 0.5 m from the detonation point under condition B3

3.2 裝藥比例埋深的影響

圖16 是工況B1～B10 下1.0 ms 時的壓力云圖，為了方便對比，壓力云圖截取了炸藥周圍2.5 m×3.5 m 的區域。圖16 的壓力云圖采用了相同的標尺，可以發現相同時刻下，隨著裝藥比例埋深的增加，黃土中直接地沖擊的作用范圍和壓力值逐漸增大，而接近地面處空氣沖擊波的作用范圍和壓力值逐漸減小。

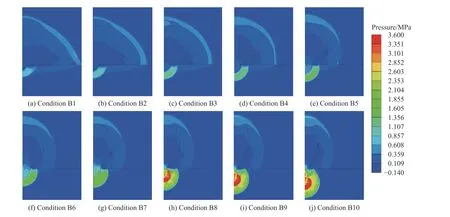
圖16 工況B1～B10 下1.0 ms 時的壓力云圖Fig. 16 Pressure contours at 1.0 ms under conditions B1-B10

圖17 以工況B3 為例，給出了數值模擬的總能量時程曲線和計算模型中空氣、黃土和TNT 的動能時程曲線。由圖17(a)可知，在6.4 ms 左右，空氣沖擊波到達流出邊界，隨后空氣沖擊波溢出流出邊界，導致計算模型的能量逐漸降低。在6.4 ms 時，能量守恒誤差為2.479×10J，計算模型能量為5.377×10J，能量守恒誤差約為計算模型能量的0.46%；在計算終止時刻10 ms 時，能量守恒誤差為2.532×10J，計算模型能量為4.898×10J，能量守恒誤差約為計算模型能量的0.52%。由圖17(b)可知，計算模型中空氣、黃土和TNT 炸藥的動能達到峰值的時間均在1 ms 以內，此時空氣沖擊波尚未溢出流出邊界。

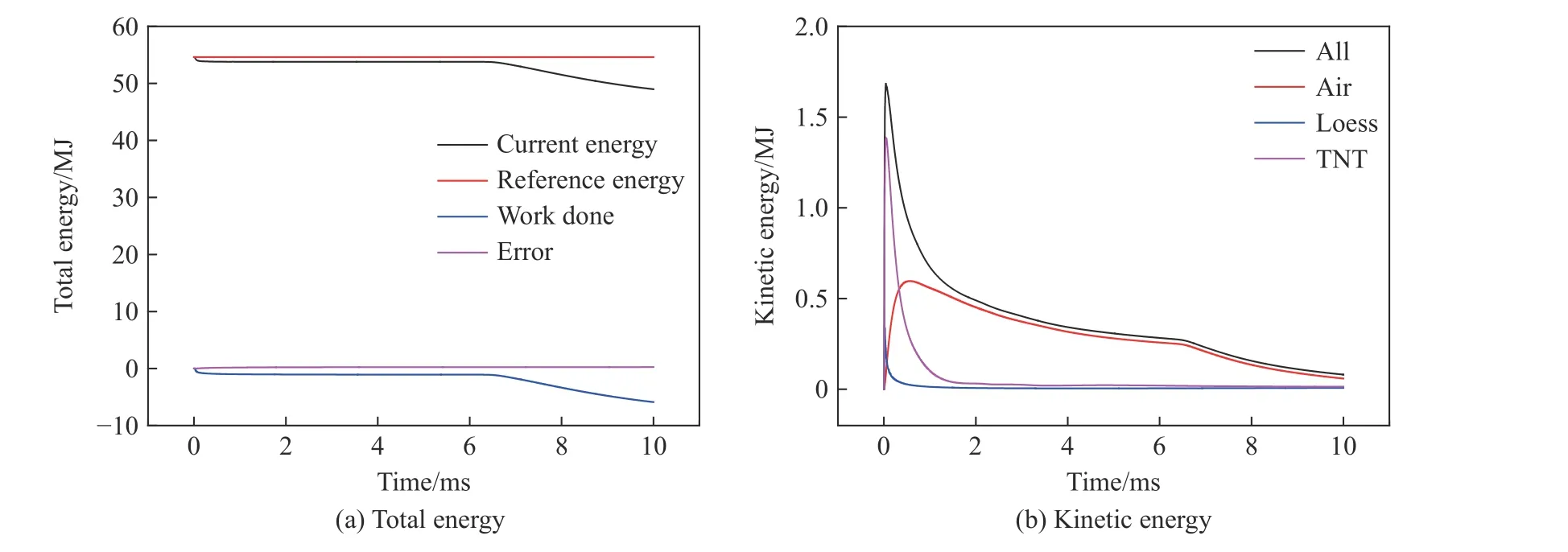
圖17 工況B3 下的能量時程曲線Fig. 17 Energy time history curves under condition B3

圖18 給出了空氣和黃土的動能峰值隨裝藥比例埋深的變化情況。隨裝藥比例埋深的增加，空氣的動能峰值迅速減小，在裝藥比例埋深達到0.1 m/kg后趨于穩定；黃土的動能峰值迅速增大，在裝藥比例埋深達到0.05 m/kg后趨于穩定。這說明隨著裝藥比例埋深的增加，空氣沖擊波獲得的能量越來越少，更多的能量耦合進入黃土介質，這將導致感生地沖擊影響范圍減小。

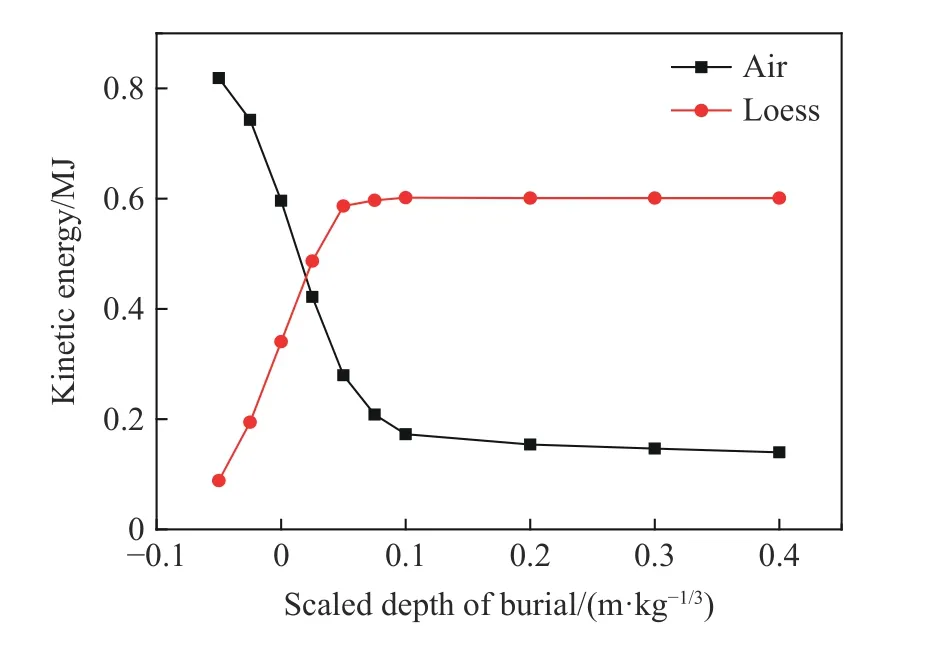
圖18 工況B1～B10 下空氣和黃土的動能峰值隨裝藥比例埋深的變化Fig. 18 Peak kinetic energy of air and loess varying with charge scaled depth of burial under conditions B1-B10

如圖19(a) 所示，以地平線為角的一條邊，以對稱軸和地平線的交點為頂點；從距離點水平距離500 mm 處的點向下選取數據測點。通過對比分析點正下方不同深度處數據測點的壓力時程曲線，同時根據壓力云圖中波陣面經過數據測點的大致時間，可以發現，隨著深度的加深，感生地沖擊壓力峰值迅速減小。在一定深度后，從壓力時程曲線上只能觀察到直接地沖擊峰值，觀察不到感生地沖擊峰值。圖19(b)僅展示部分數據測點，實際為了判斷準確，所取數據測點間隔更小。存在某一深度處測點的壓力時程曲線從2 個明顯的峰值轉變為1 個明顯的峰值，取這一點為點，用90°減去∠即為γ 的大小。然后，對比點和點之間的數據測點的豎向應力時程曲線（見圖19(c)），可以發現，隨著深度的增加，感生地沖擊豎向應力峰值減小，直接地沖擊豎向應力峰值增大。存在某一深度處測點的豎向應力時程曲線中，感生地沖擊和直接地沖擊的豎向應力峰值相等，取這一點為點，則∠=α，∠-∠=β。

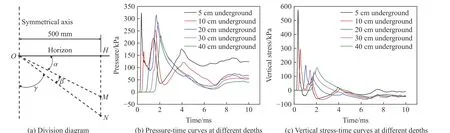
圖19 α、β 和γ 的取值方法Fig. 19 Determination methods of α, β and γ

圖20 給出了工況B1～B10 下的數值模擬結果。其中，α、β 和γ 分別表示圖13 中地表區、近地表區和中心區的角度，且α、β 和γ 三者之和為90°。隨裝藥比例埋深的增大，α、β 和γ 的變化呈較強的規律性。

圖20 工況B1～B10 下地沖擊作用區的角度隨裝藥比例埋深的變化Fig. 20 Angles of ground shock subzones varying with charge scaled depth of burial under conditions B1-B10

(1)當裝藥比例埋深為-0.05～0.075 m/kg時，地沖擊作用區角度的變化較劇烈。隨著裝藥比例埋深的增加，中心區的角度γ 迅速增大，地表區的角度α 迅速減小，近地表區的角度β 逐漸增大。

(2)當裝藥比例埋深為0.1～0.4 m/kg時，地沖擊作用區的角度趨于穩定。

3.3 炸藥類型的影響

圖21 為工況C1～C12 下1.0 ms 時的壓力云圖，同樣截取了炸藥周圍2.5 m×3.5 m 的區域。圖22 給出了不同工況下空氣和黃土的動能峰值的變化情況。不同工況下，直接地沖擊和感生地沖擊壓力值不同，爆炸耦合進入空氣和黃土介質動能存在差異，這將引起不同工況地沖擊作用區角度的變化。

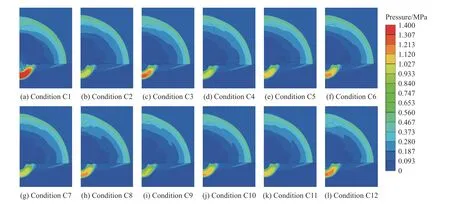
圖21 工況C1～C12 下1.0 ms 時的壓力云圖Fig. 21 Pressure contours at 1.0 ms under conditions C1-C12

圖22 工況C1～C12 下空氣和黃土的動能峰值Fig. 22 Peak kinetic energy of air and loess under conditions C1-C12

表7 給出了工況C1～C12 下的數值模擬結果。表7 中：為水平爆心距0.5 m 處地面空氣沖擊波超壓峰值，σ為爆心正下方0.5 m 處直接地沖擊應力峰值，其位置可參見圖6(b)）中A1 和S1 測點；為水平爆心距0.5 m 處地面空氣沖擊波超壓的沖量，為爆心正下方0.5 m 處直接地沖擊應力的沖量。由圖23可知，/隨炸藥爆速和爆壓的升高呈增大的趨勢，即隨著炸藥爆速和爆壓的升高，地面空氣沖擊波超壓的沖量增大，而直接地沖擊應力的沖量減小。

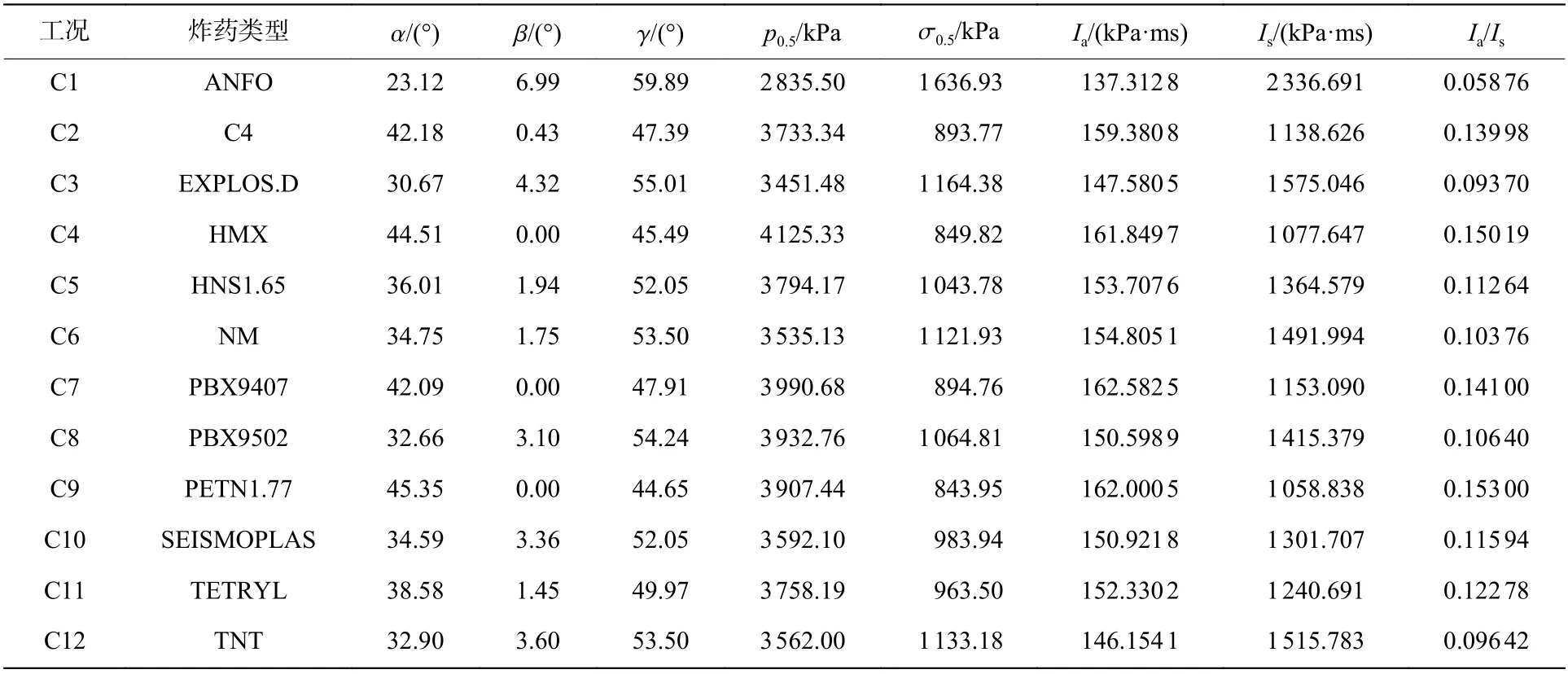
表7 工況C1～C12 下的數值模擬結果Table 7 Numerically simulated results under conditions C1-C12

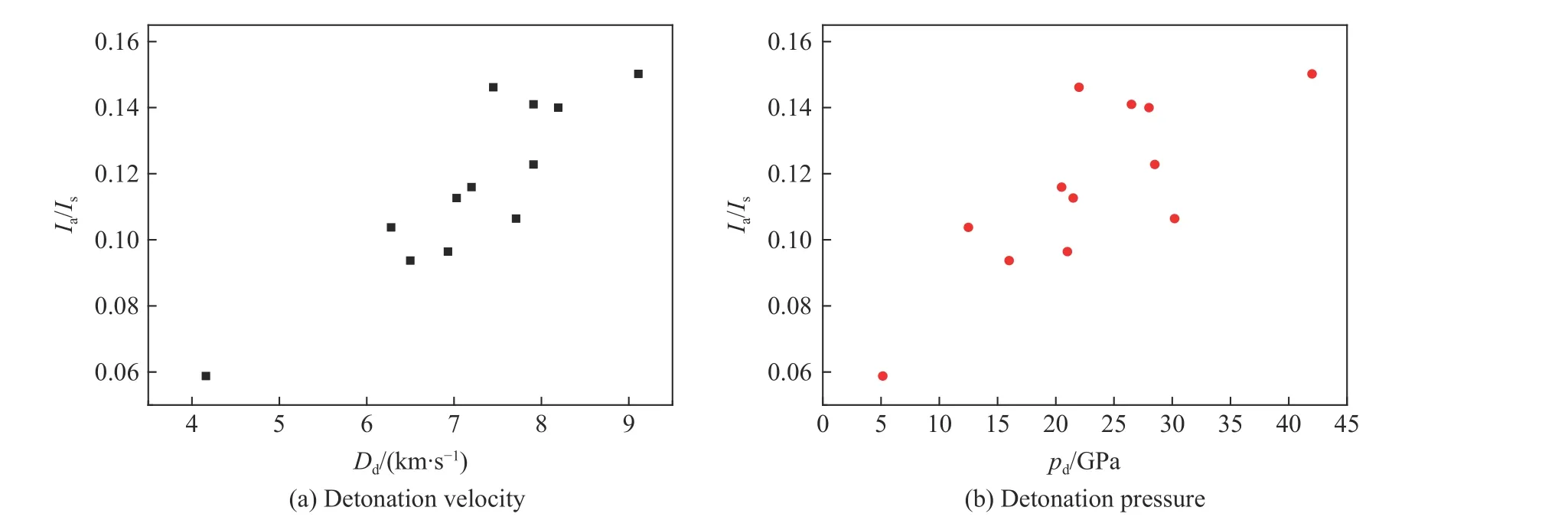
圖23 Ia/Is 隨炸藥爆速和爆壓的變化Fig. 23 Variation of Ia/Is with detonation velocity and detonation pressure of explosive

經分析，發現當/的取值范圍為0.058 76～0.153 00 時，地沖擊作用區角度與地面空氣沖擊波超壓沖量和直接地沖擊應力沖量之比呈線性相關關系（見圖24），擬合后可得到：

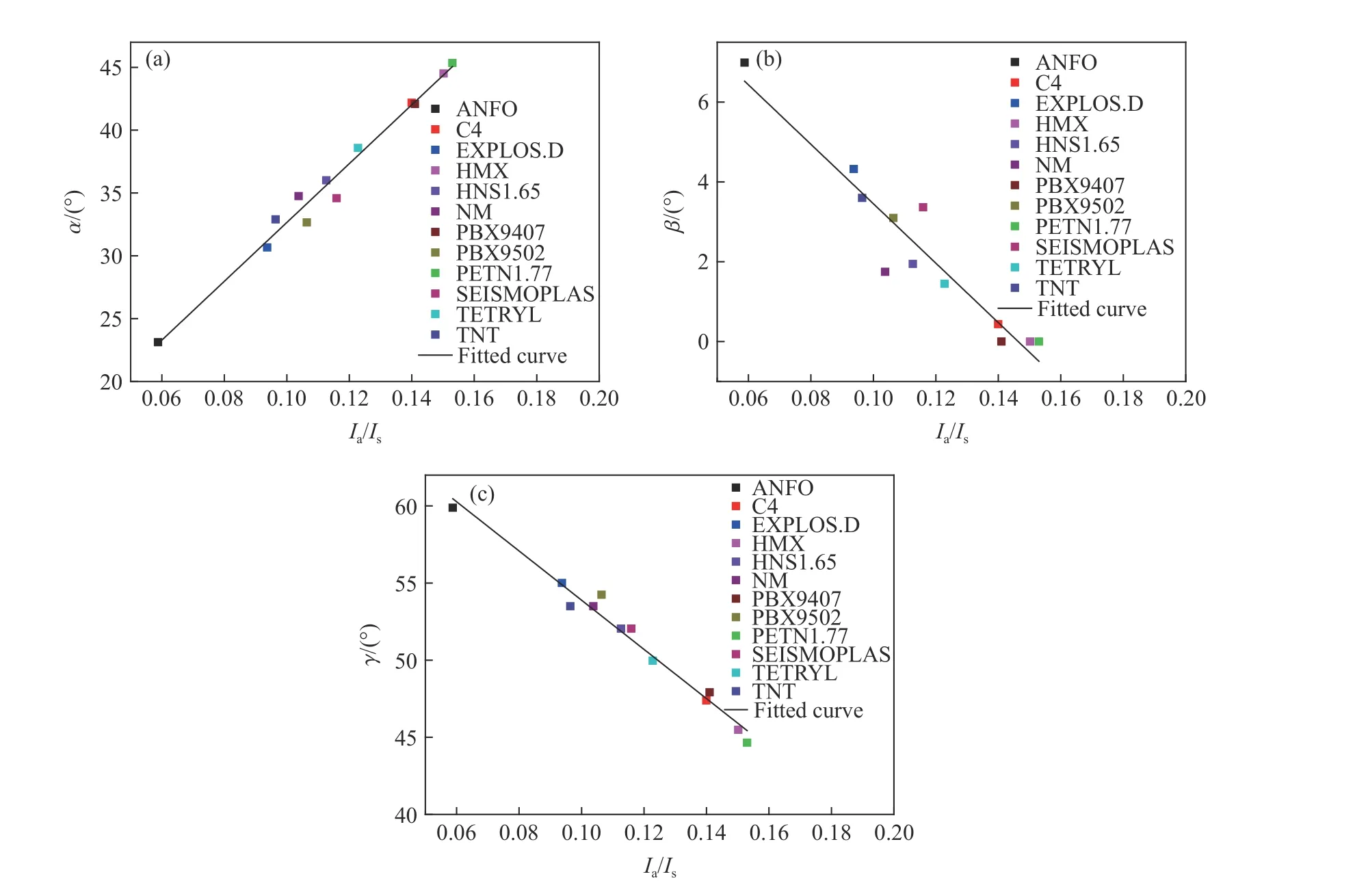
圖24 α、β 和γ 隨Ia/Is 的變化Fig. 24 Variation of α, β and γ with Ia/Is

式中：α、β 和γ 的單位均為(°)。

4 結 論

針對土中爆炸應力波的時空分布問題，以數值模擬分析為主要手段，并輔以土中爆炸試驗，得到以下主要結論。

(1)通過黃土中接觸爆炸和半埋爆炸試驗，得到了不同比例爆距上地面空氣沖擊波超壓和土中直接地沖擊豎向應力，并以此驗證了所建立計算模型的有效性。

(2)根據土中不同深度壓力和豎向應力的特征，將土中應力波場劃分為地表區、近地表區和中心區。地表區的時程曲線出現2 個峰值，且感生地沖擊起主導作用；近地表區的時程曲線同樣出現2 個峰值，且受感生地沖擊和直接地沖擊的聯合作用；中心區的時程曲線僅出現1 個峰值，主要受直接地沖擊的作用。

(3)通過研究不同裝藥比例埋深爆炸工況，發現當裝藥比例埋深為-0.05～0.075 m/kg時，隨著裝藥比例埋深的增加，土中應力波場的中心區迅速增大，地表區迅速減小，近地表區逐漸增大；當裝藥比例埋深為0.1～0.4 m/kg時，地沖擊作用區的分布趨于穩定。

(4)通過研究裝藥比例埋深為0.0 m/kg時，不同類型炸藥爆炸工況，發現隨著炸藥爆速和爆壓的增加，地面空氣沖擊波超壓的沖量增大，而直接地沖擊應力的沖量減小，在一定范圍內，地沖擊作用區角度與地面空氣沖擊波超壓沖量和直接地沖擊應力沖量之比呈線性相關關系。