基于經驗模態分解的螺栓連接狀態敲擊檢測方法

劉俊燚，李寧，姜玉虎，李美求

(1.長江大學結構強度與振動研究所，湖北荊州 434023；2.江蘇省油(氣)井設備工程技術研究中心，江蘇鹽城 224000；3.江蘇宏泰石化機械有限公司，江蘇鹽城 224000)

0 前言

螺栓連接廣泛應用于工程現場連接結構中，螺栓連接結構容易拆裝，降低了大型設備的運輸成本。在含有螺栓連接的各種設備中，設備工作時螺栓的松動是一個不可避免的問題，全球每年約有20%的機械故障是由于螺栓松動引起的。并且在整個結構中，螺栓是比較薄弱的一個部位，一旦發生松動或者脫落，可能造成整個設備失效，嚴重的甚至威脅到人的生命財產安全。為避免螺栓松動，國內外學者對彈簧墊圈、雙螺母、楔形墊圈以及非金屬墊片等螺栓防松結構進行了大量相關研究，并證明了其在螺栓連接防松應用的有效性。但是現有防松結構的防松機制主要是靠摩擦防松或者張力鎖緊防松，實際應用中存在安裝拆卸不方便、螺紋強度差或者受溫度影響顯著等缺點。而開發一種低成本、簡單可靠的螺栓在線監測方法既可以簡化螺栓連接結構，又可以得到螺栓連接狀態的及時反饋，進而保證整個系統的穩定運行。

常規的螺栓健康檢測方法有敲擊法、扭力扳手法、電阻應變片法等，其中扭力扳手法在工程實際中應用較為廣泛。但是由于螺紋副與零件、螺栓與零件之間均存在摩擦且摩擦較為分散，扭力扳手測得的結果并不準確，同一規格的螺栓在相同扭矩下的預緊力誤差甚至可以達到50%，并且受到螺栓安裝位置的限制，扭力扳手在一些情況下無法對螺栓擰緊力進行快速檢測。隨著智能材料的發展，利用壓電材料對螺栓的擰緊狀態進行檢測得到快速的發展。但是利用壓電片對螺栓狀態進行檢測大部分應用于實驗室條件，在工業上沒有得到廣泛的應用。通過在螺栓上粘貼電阻應變片，測量應變片形變可以直觀地反映出螺栓的形變，在工業上得到較為廣泛的應用。但是螺桿的表面是曲面，在其表面粘貼受到了一定程度的限制。在實際應用中，一個設備上安裝的螺栓數目很多，若在每個螺栓上都安裝應變片會帶來較高的經濟成本、時間成本。在螺栓狀態監測方法的實際應用中，敲擊法由于操作方便、對工作環境要求較低等原因可以較好地應用在實際工程中。

作為一種方便快捷的檢測方法，敲擊法最早的應用是使用硬幣敲擊構件表面，通過敲擊聲音判斷構件是否有結構性損傷。在日常生活中，鐵路工人通過敲擊鐵軌表面的聲音判定鐵軌是否有裂縫，建筑工人在鋪地磚時用錘敲擊地磚表面檢查地磚下面是否有空洞。傳統的通過敲擊判斷結構損傷的方法雖然簡單，但是非常依賴人工經驗，沒有可以進行量化的標準。在理論上對敲擊信號進行解釋，最早是CAWLEY、ADAMS通過實驗發現結構缺陷處被敲擊時的聲音信號與正常區域不同是因為敲擊時力在結構中的傳遞發生了變化而造成的。WANG、SONG使用新開發的一維記憶增強卷積長短期記憶網絡方法對鋁制框架結構的敲擊信號進行分析并證明了新方法對螺栓狀態識別的有效性。肖強宏等基于敲擊聲音建立了一套可以對陶瓷產品進行結構缺陷在線監測的系統。

隨著信號處理技術的快速發展，不斷有新的信號處理方法應用于螺栓監測信號的分析中。傅里葉變換現已廣泛應用于結構在線監測工作中，傅里葉變換是應用最為廣泛的信號處理方法，對平穩信號的分析效果較好。但是現實中大部分信號都是非平穩信號，直接使用傅里葉變換對其進行處理，結果并不理想。為此，研究人員通過對傅里葉變換算法進行改進或者與其他信號處理方法相結合來更好地提取信號中包含的信息。在這些新的結構監測方法中，短時傅里葉變換、小波變換等方法得到了較多的應用，但是傳統的短時傅里葉變換的時頻窗口大小不變，沒有自適應特性；小波分析雖然有可調的自適應窗口，但本質上仍然是一種窗口可調的傅里葉變換，依舊沒有擺脫傅里葉變換的局限性。

美籍華人HUANG等在1998年提出了經驗模態分解(Empirical Mode Decomposition，EMD)算法，這種方法對非平穩、非線性信號具有比較好的分析效果，可以對信號進行時頻域上的自適應分析，EMD算法在HUANG等提出后廣泛應用于結構健康領域。ZHOU等通過對含有螺栓的框架結構施加激勵，并利用EMD能量損傷指標反映螺栓的連接狀態，實驗結果表明EMD能量指標對螺栓早期的松動更為敏感。PEREZ-RAMIREZ等通過EMD方式成功實現了對高層建筑振動信號中高頻噪聲的處理。周文強等利用EMD分解后的第一階IMF分量構造能量損傷指標識別螺栓的損傷狀態。

本文作者提出一種新的基于敲擊聲對螺栓連接狀態進行分析的方法，使用經驗模態分解對7種擰緊力矩下的螺栓敲擊聲信號進行分解，取分解后的前兩階IMF分量進行頻譜分析，觀察峰值點的頻率值隨螺栓擰緊力矩的變化趨勢，并與原信號的頻譜圖進行對比，通過實驗驗證了該方法對螺栓連接狀態檢測的有效性。

1 理論分析

1.1 敲擊信號檢測機制

作為典型的非線性動力學問題，螺栓連接界面邊界條件的時變性和接觸非線性造成了連接界面剛度和阻尼的非線性。在實際生產工作中，螺栓連接中存在著接觸、摩擦和預緊的耦合關系，在動態激勵下，非線性耦合激勵更為復雜，難以建立準確的數學力學模型。有學者研究發現螺栓預緊力的大小對螺栓法向接觸剛度影響較大，預緊力越大，法向剛度越大，同時結構的固有頻率隨著結構剛度的增大而增大。因此可通過分析敲擊螺栓連接部位信號的內在特征來實現對螺栓擰緊力矩的監測。作者主要是通過敲擊信號檢測螺栓的擰緊力矩，因而不對非線性動力學做細節上的分析，只尋找敲擊信號隨螺栓擰緊力矩變化的相關特征。

1.2 EMD算法原理

EMD算法將一個復雜的信號分解為若干個本征模式分量之和，這基于一個假設，假設任何復雜信號都是由一些不同的分量(IMF)組成。每個IMF分量都必須滿足下面兩個條件:(1)極值點個數和過零點的數量相同或最多相差1個；(2)分量的上下包絡線關于時間軸局部對稱。這樣，任何一個信號就可以分解為有限個IMF之和，在此假設的基礎上，任何信號都可以通過采用EMD方法來進行分解。而IMF可以按以下方法“篩選”獲得：

(1)找到信號的所有局部極值點，將所有的局部極大值點用三次樣條線連接起來，形成上包絡線。

(2)同理，將所有局部極小值點用三次樣條線連接起來形成下包絡線，上、下包絡線應將所有采集的數據點都包含進去。

(3)上、下包絡線的平均值記為，求出

()-=

(1)

理想情況下，如果是一個IMF，那么就是()的第1個IMF分量。

(4)如果不滿足IMF的條件，把作為原始數據，重復步驟(1)—(3),得到上、下包絡線的平均值，再判斷=-是否滿足IMF的條件，如不滿足則繼續重復次，得到1(-1)-1=1使得1滿足IMF的條件。記=1，此時，為信號()的第一個滿足IMF條件的分量。

(5)將從()中分離出來，得到

=()-

(2)

將分離出來后，再將作為原始數據繼續重復步驟(1)—(4)，直至得到()滿足IMF條件的第二個分量。重復循環次，得到信號()的第個滿足IMF條件的分量。這樣就有

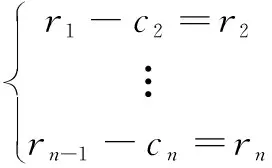
(3)

當變成一個單調函數，不能再從中提取出滿足IMF條件的分量時，循環結束。這樣由式(2)和式(3)得到

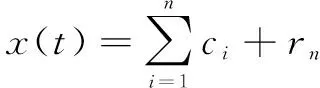
(4)

式(4)中：是殘余函數，代表信號的平均趨勢。

所以，通過經驗模態分解可以把任意一個信號()分解為階IMF分量和一個余項之和，螺栓的敲擊信號是非平穩、非線性的信號，并且信號較為復雜，對其進行經驗模態分解處理可以將信號包含的各分量分解為不同的階數。

2 實驗研究

2.1 實驗設備

螺栓擰緊力矩檢測實驗裝置如圖1所示：實驗設備包括M10的螺栓，螺母和墊片組合，尖頭小錘，內六角扳手，墊在試件下的泡沫，量程10～200 N·m、測量精度為0.1 N·m的定扭矩扳手；實驗所用數據采集設備為MPS-010602信號采集卡和YAVZ2環境聲音傳感器，信號采集卡的采樣率為5～80 kSps，此實驗中信號采樣率為48 kHz，A/D精度為14位，錄音環境在較為安靜的室內。

圖1 實驗裝置

2.2 實驗過程

為獲取螺栓連接在擰緊力矩不同的條件下，聲音信號在時頻域上的特征，用小錘敲擊螺母側邊并使用聲音傳感器對敲擊聲信號進行采集。此次試驗共采集了擰緊力矩分別為0、10、15、20、25、30、35 N·m時的螺栓敲擊聲信號，其中0 N·m即為螺栓完全松動的狀態，采集信號時要保持敲擊螺栓的力度不發生劇烈變化。對上述7種螺栓狀態分別進行20次測試，增加樣本數量的同時減少了偶發情況對數據集的影響。

3 實驗結果及討論

從圖2中可以發現：在不同擰緊力矩下，敲擊信號的時域信號圖并不能很直觀地反映出信號與擰緊力矩的關系。而頻譜圖可通過觀察峰值點頻率值尋找隨擰緊力矩變化的規律，下面對信號做傅里葉變換，進行時頻分析。

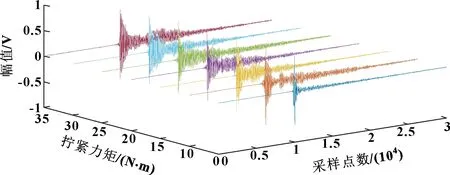
圖2 不同擰緊力矩敲擊下的時域信號圖

3.1 頻域分析

傅里葉變換是以時間為自變量的信號和以頻率為自變量的頻譜函數之間的一種變換關系。自變量時間和頻率可以是連續的，也可以是離散的。傅里葉變換是一種線性的積分變換，這種變換是從時間轉換為頻率的變換或者從頻率域轉換到時間域上，一些在時域上沒有明顯特征的信號通過傅里葉變換可以簡單地從頻域上提取出相應的信息。

快速傅里葉變換是離散傅里葉變換的一種快速算法。對不同工況下的敲擊信號進行快速傅里葉變換(FFT)處理，得到不同擰緊力矩下敲擊螺母的聲信號在頻域上的特征。圖3—圖6為不同擰緊力矩下的頻譜。

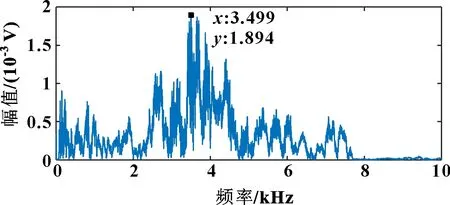
圖3 擰緊力矩為0 N·m時的頻域

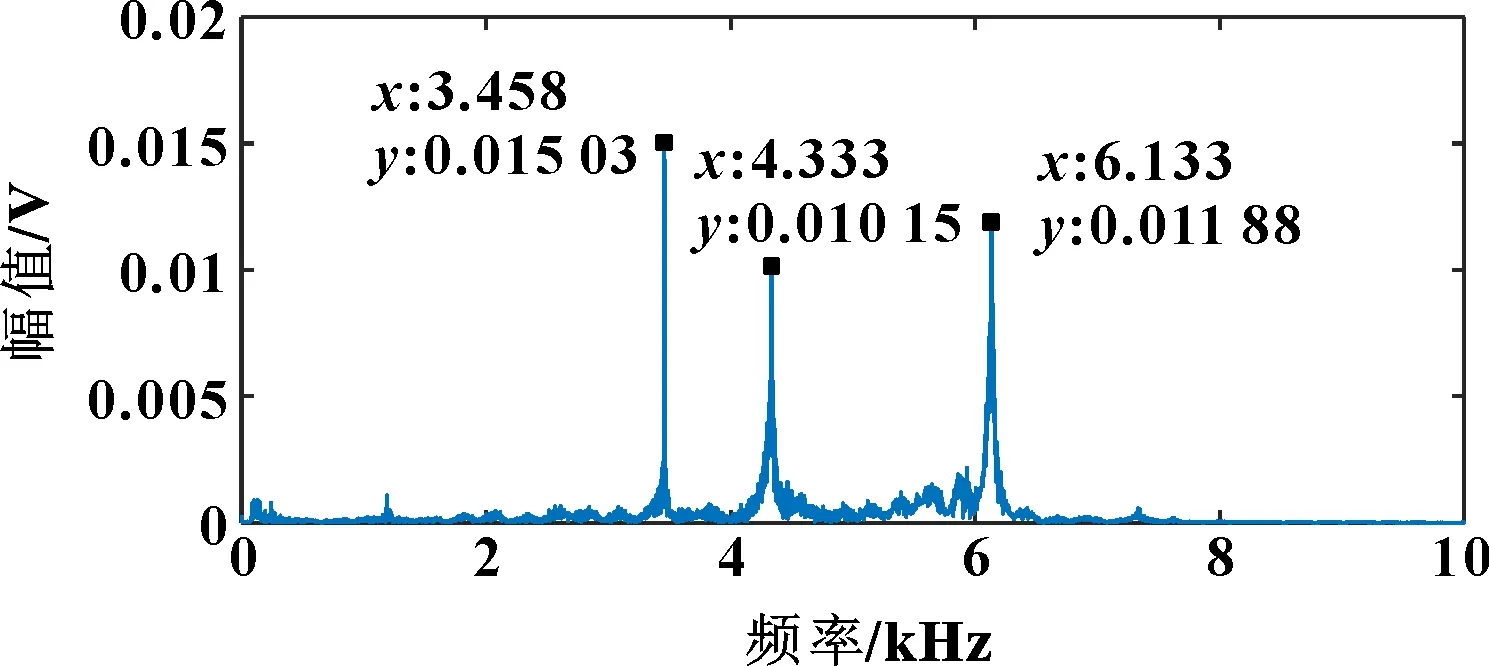
圖4 擰緊力矩為10 N·m時的頻域

圖5 擰緊力矩為20 N·m時的頻域

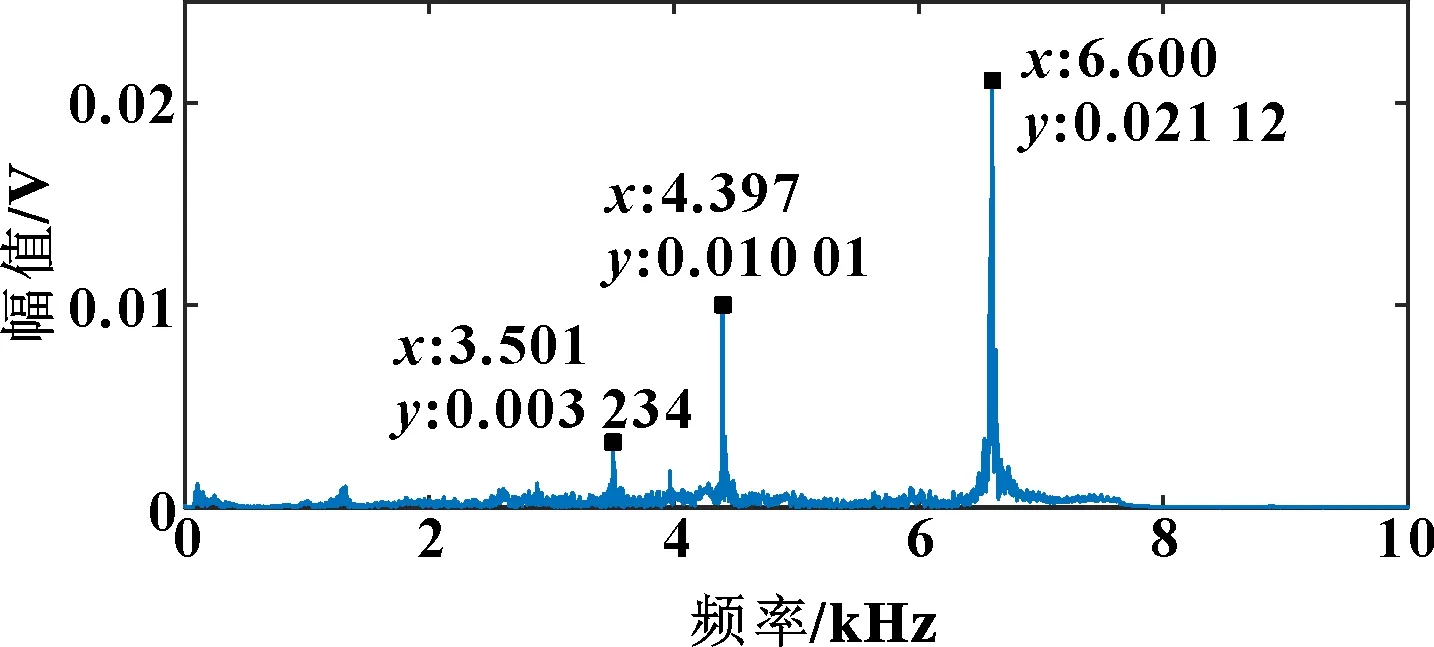
圖6 擰緊力矩為30 N·m時的頻域

圖7反映了不同擰緊力矩下敲擊聲信號經傅里葉變換后的3個峰值點對應的頻率隨擰緊力矩變化的規律。

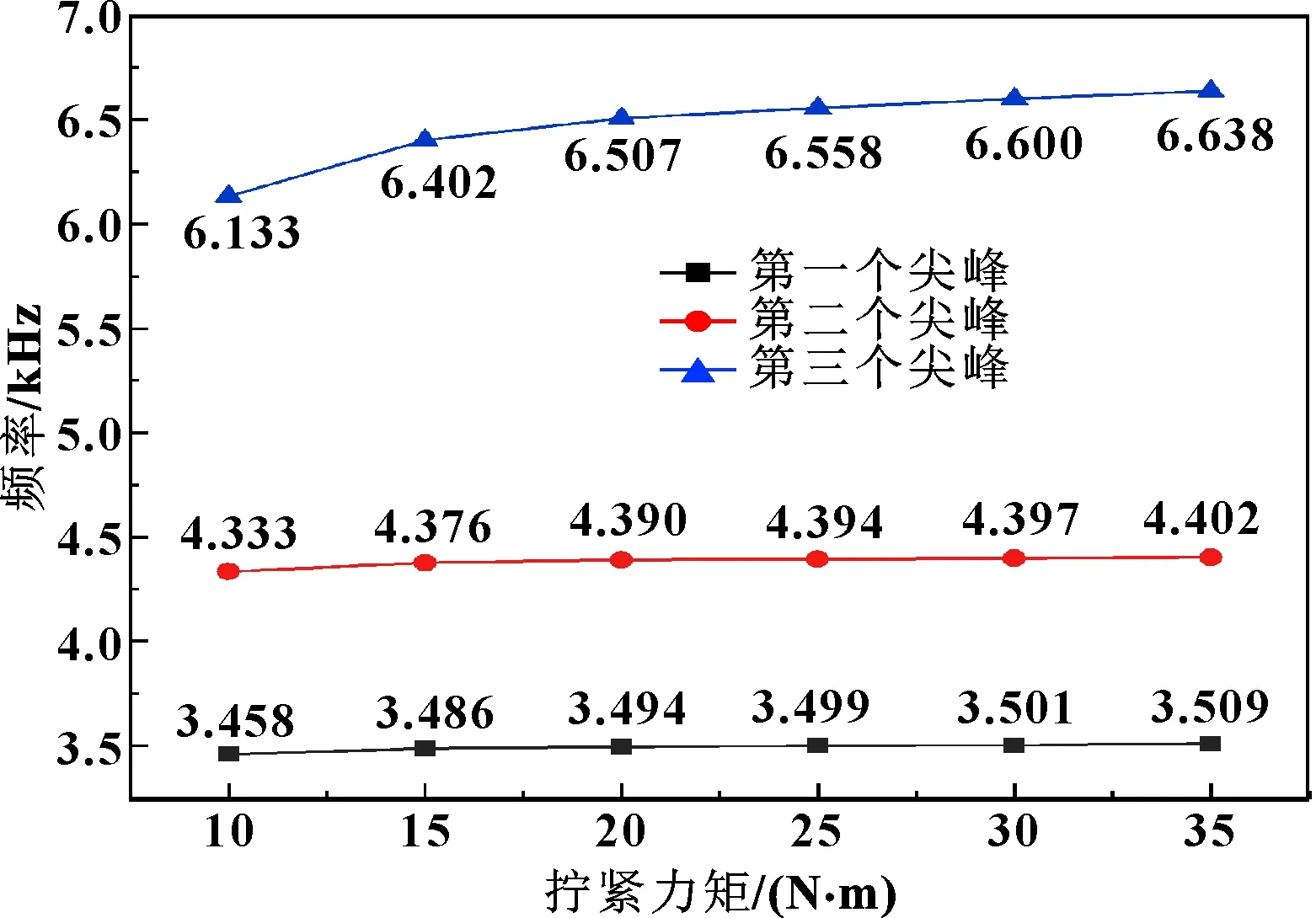
圖7 不同擰緊力矩下3個峰值點的頻率值

通過觀察頻譜圖可以發現:除擰緊力矩為0時信號上只有一個峰值外，在螺栓處于有擰緊力的狀態下，頻譜圖上會出現3個峰值。進一步觀察還可以發現：3個峰值都會隨著擰緊力矩的增大向高頻方向偏移，這說明螺栓連接的剛度隨擰緊力矩增大而增加。連接剛度主要是通過螺母與螺帽之間接觸的緊密程度表現出來的，和擰緊力矩有直接的相關關系。

定義主頻為原始波形信息經過傅里葉變換后所得到的二維頻譜圖中最大幅值所對應的頻率。雖然3個峰值分別隨螺栓擰緊力矩的增大而增大，但是主頻值在頻譜圖上散布在不同的尖峰上，并沒有確定的分布規律。

3.2 經驗模態分解

由前文傅里葉變換分析結果可知，信號集中分布在由低到高的3個峰值上，可使用經驗模態分解方法對信號進行分解，對分解后的IMF分量再做頻域分析。經EMD分解過后，信號被分解為14個IMF分量，一般認為EMD方法是一種主成分分析方法，主要的故障信息集中在前幾個IMF分量，故選用前兩階IMF分量對信號進行分析。圖8為信號經過EMD分解后的前兩階IMF分量時域信號圖。

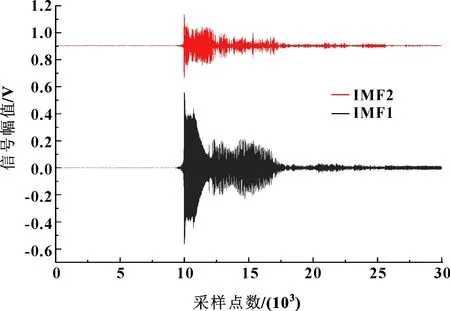
圖8 前兩階IMF信號分量

獲得信號的各階模態分量之后，分別對前兩階IMF分量進行傅里葉變換，其峰值點的頻率值如圖9、圖10所示。

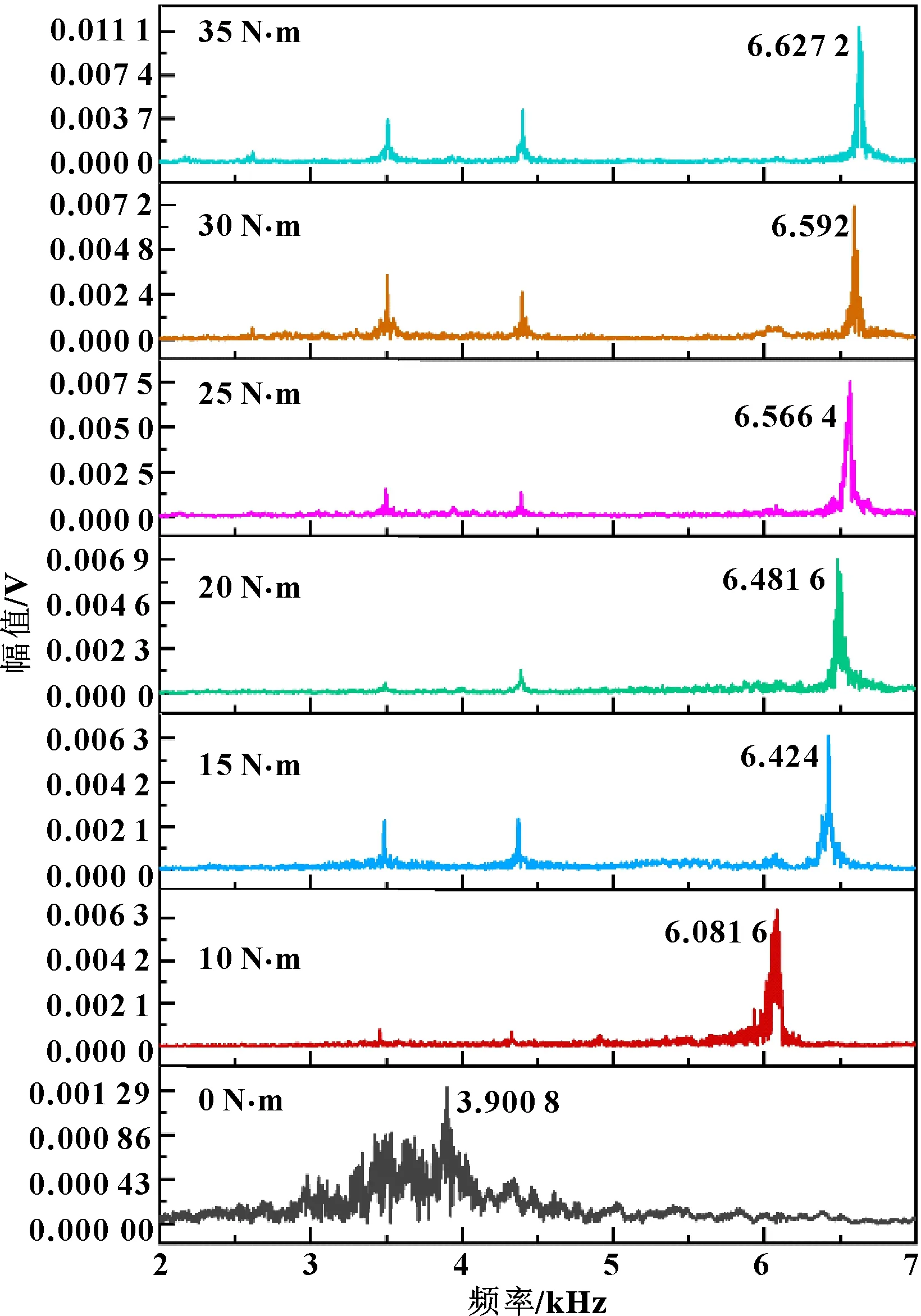
圖9 不同力矩下IMF1信號峰值點的頻率值

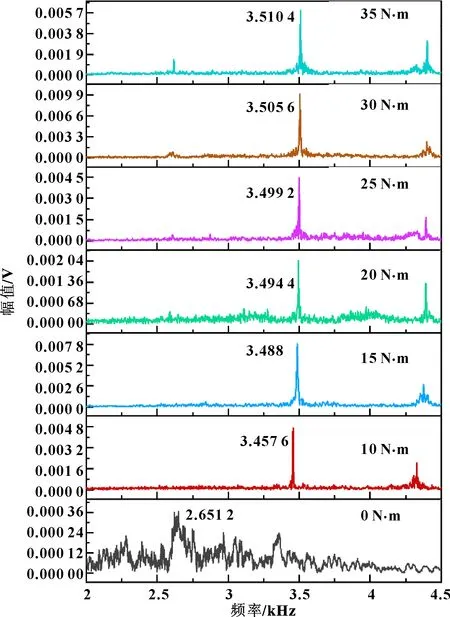
圖10 不同力矩下IMF2信號峰值點的頻率值

通過實驗數據可以發現，信號前兩階IMF分量的峰值都隨擰緊力矩增大而增大，并且從0到10 N·m的過程中峰值頻率變化趨勢最為明顯。原因是IMF1的頻率范圍在螺栓連接的固有頻率附近，螺栓從松動到擰緊狀態轉變時，螺栓連接界面之間的接觸從表面微凸體之間的點接觸變為相互嵌埋的狀態，內部接觸界面的結構發生了較大的變化；而在之后隨著擰緊力矩增大到一定程度之后，大部分連接面的接觸狀態已轉變為相互嵌埋的狀態，接觸剛度變化速度逐漸變慢。因而可以通過觀察螺栓敲擊信號的前兩階IMF信號分量來判定螺栓的連接狀態，尤其是螺栓接近或者已經松脫時，峰值頻率相較于螺栓正常連接狀態有明顯的變化。

4 結論

基于螺栓的敲擊聲信號提出了一種螺栓擰緊力矩的無損檢測方法。通過上述研究，可以得出以下結論：

(1)在不同擰緊力矩下，螺栓的敲擊聲信號經傅里葉變換處理，在頻譜圖上可觀察到有3個明顯的尖峰，但是3個峰值點幅值之間的大小關系并沒有很明顯的規律；

(2)原始信號經EMD分解后，前兩階IMF分量都有很明顯的峰值頻率，并且峰值頻率的大小都與擰緊力矩呈正相關，可以反映螺栓的連接狀態；

(3)螺栓的擰緊力矩在從0到10 N·m的過程中峰值頻率變化趨勢最為明顯，說明在螺栓即將松脫時，兩階模態分量的峰值頻率對螺栓的連接狀態變化更為敏感。

由于檢測方法的便捷，該方法在工程實際中有較好的應用價值，但是通過觀察信號兩階模態分量隨螺栓擰緊力矩的變化趨勢可以看出：隨著擰緊力矩的增加，峰值頻率增長速度逐漸放緩，在螺栓松脫程度比較小時，擰緊力矩對IMF1與IMF2峰值頻率的影響都較小，對螺栓連接狀態的檢測精度較低；而螺栓接近松脫時，峰值頻率變化曲線相對陡峭，此時，對螺栓連接狀態的判斷比較準確。對螺栓松脫程度較小時的狀態可以作為接下來的研究內容。