柔性機座-轉子系統動力學參數優化仿真

孫志，買買提明·艾尼，尼加提·玉素甫

(新疆大學機械工程學院，新疆烏魯木齊 830049)

0 前言

隨著旋轉機械向高轉速、大跨度、柔性輕結構方向發展，轉子系統的偏心、剛度、阻尼和質量及自身結構復雜性等因素的影響引起的穩定性問題日益突出。

為了解決此問題，早在1972年，KIRK和GUNTER提出了對轉子系統應用動態阻尼器設計的固定點理論(PQ點理論)。1997年，郭增林等在固定點理論的基礎上提出了虛擬振幅法，從而解決了滑動軸承-轉子系統的最優彈性阻尼器匹配問題。2002年， ISHIDA、INOUE用固定點理論計算結果和用動態吸振器的實驗測試結果對比研究了轉子軸承系統的非線性影響，通過動態吸振器的最優設計獲得了與線性相同的減振效果。2015年，RIBEIRO等針對黏彈性機座的優化設計提出了一種基于廣義當量參數的方法，并通過使用混合優化技術達到了使頻率不平衡響應最小化的目的。2016年，SHEN等利用負剛度的動態吸振器來降低系統振幅，發現在幅頻曲線上仍然存在3個不動點，而通過利用固定點理論計算，獲得了支承最優剛度阻尼比。黑棣等人以轉軸剛度為控制參數，運用改進的 Newmark 法研究了拉桿轉子的動力學特性，同時通過改變支點比和預負荷來研究轉子系統動力穩定性，發現當轉軸剛度、預負荷和支點比的匹配域范圍合理時，轉子運動更穩定。徐璐等人采用數值積分法,發現偏心量的取值會對系統狀態產生顯著影響。

買買提明·艾尼提出了基于“窮舉法”的一種新的動力學參數最優匹配方法。通過在合理的給定域內離散支承剛度和阻尼、并在合理的給定轉速范圍內進行數值計算，從而獲得支承剛度和阻尼與其他給定動力學參數相互匹配的最大振幅比及其分布范圍，并用窮舉法獲取支承參數的最優匹配點及其最優匹配軌跡。然而轉子系統的理論計算過程十分復雜，有必要針對全局動力學參數下的最佳支承參數匹配進行軟件開發研究和軟件平臺建設。

作者將根據柔性機座-轉子軸承系統全局最優參數匹配及其非線性動力學方程組的數值建模理論、關鍵算法，詳細研究全局參變量的變化形式、編程技巧和算法技術，架構設計數值軟件系統總體結構，編程實現高效的數值計算軟件集成，同時建立方便的動力學參數全局最優匹配數值建模方法，為高效快速最優匹配數值分析和非線性振動分析提供軟件平臺，并以M701F重型燃氣輪機轉子系統作為研究背景進行可行性驗證。

1 RSS機座-軸承轉子系統動力學模型

燃氣輪機透平端RSS機座支承的軸承-轉子系統是復雜的多質量、非對稱的系統。而機座在大參數、高速、高溫、重載轉子系統中，不僅起到支承的作用，而且在轉子振動時對吸收能量和降低轉子振幅也有重大作用。因此，RSS機座-軸承轉子系統動力學參數的相互匹配將直接影響系統的穩定性。為了方便研究RSS機座的最優動力學參數匹配點及軌跡，本文作者將實際的RSS機座-軸承-轉子系統簡化成如圖1所示的對稱機座-軸承-轉子(Jeffcott)系統，并建立了圖1(a)和(b)所示的力學模型和計算坐標，可建立圖1所示的力學模型。

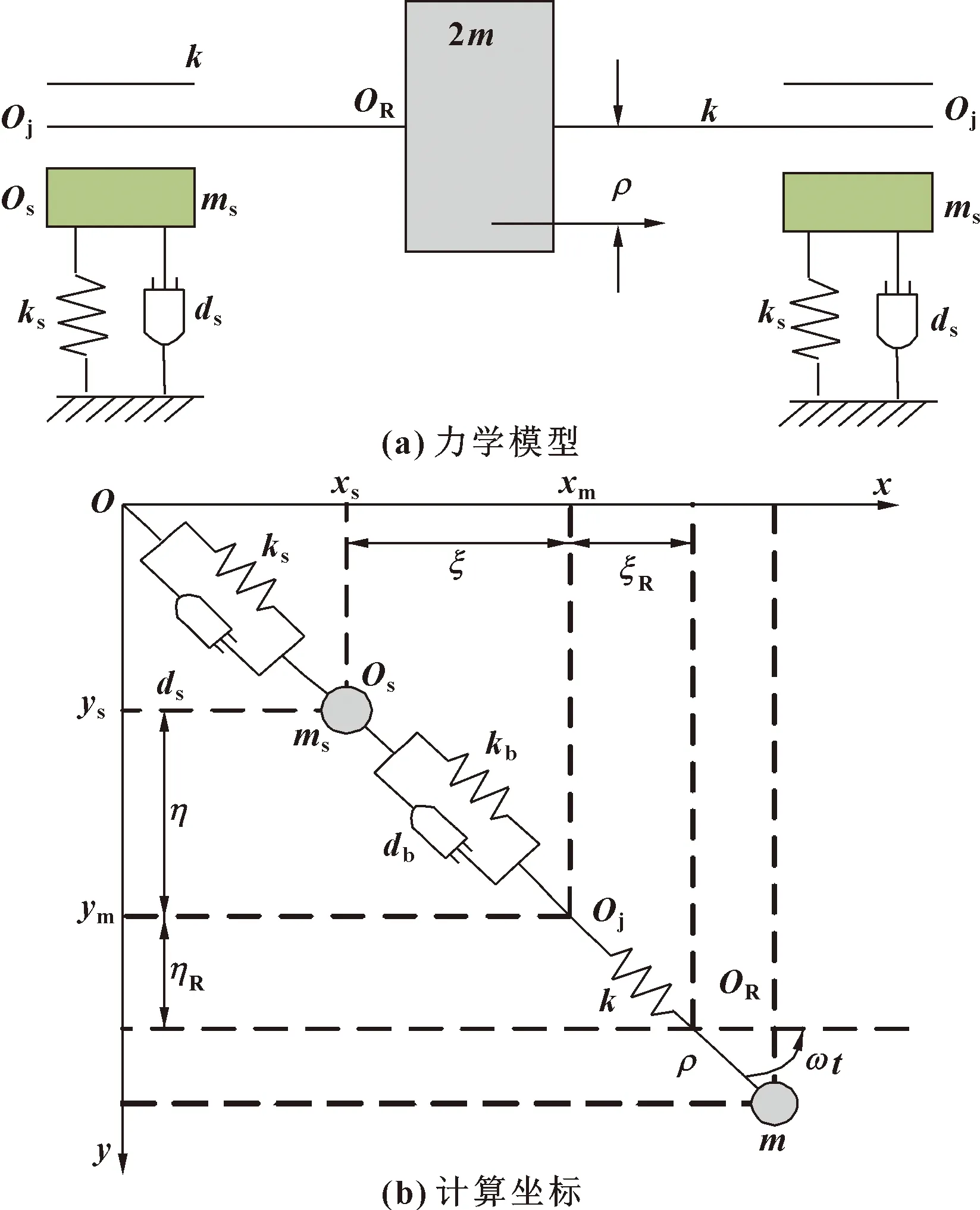
圖1 RSS機座-軸承-轉子系統簡圖

對于單質量圓盤近似的轉子來說有：

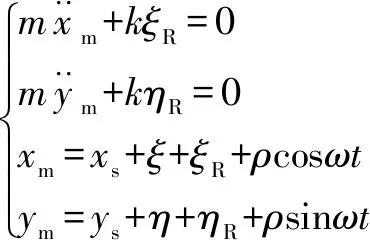
(1)

對于轉子與滑動軸承來說有：

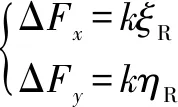
(2)

對于RSS支承座有：

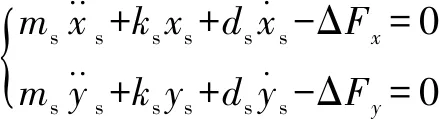
(3)

式中：為單質量圓盤近似的轉子質量；為轉子軸剛度；、、分別為RSS支承座的質量、剛度和阻尼；為質量偏心距。

滑動軸承在向轉子系統提供阻尼方面比滾動軸承更有效，因而對于大型轉子系統，常采用滑動軸承可以較好地減小振動。為了方便起見，滑動軸承設為固定瓦徑向滑動軸承，這時軸頸中心和方向偏離靜態工作點時所產生的油膜力增量為

(4)

式中：、(,=,)分別為油膜剛度和阻尼系數。

固定瓦徑向滑動軸承的動力特性采用8個系數來描述。如公式(5)所示：

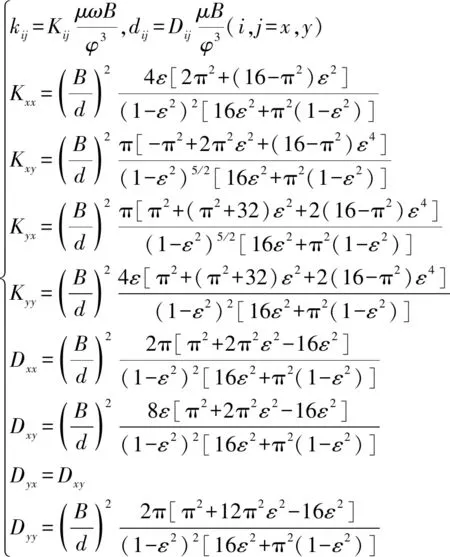
(5)

式中：為軸承寬度；為軸承內直徑；為潤滑油膜動壓黏度；偏心率=；=為間隙比；為軸承的半徑間隙；為軸承內半徑；(,=,)為相應的量綱一剛度系數；(,=,)為相應的量綱一阻尼系數。

令:

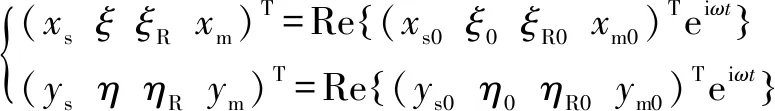
(6)

以上、、…、、為復振幅。

圓盤振幅計算公式:

(7)

式中：=/60為轉動頻率，為轉速；為圓盤最大振幅；、分別為圓盤在和方向移動的位移。

2 動力學參數全局最優匹配方法

作者基于上述柔性RSS機座-軸承轉子系統動力學模型與相關動力學公式，推導出系統的轉子頻率、振幅和支承質量、阻尼、剛度之間的關系式，提出了全局最佳匹配分析法。系統動力學參數最佳匹配就是在柔性RSS機座軸承轉子系統參數中尋找能使系統振幅比達到較小的參數。因此本文作者將系統的轉子及機座參數設為最佳匹配的設計變量，全局匹配分析方法示意如圖2所示。

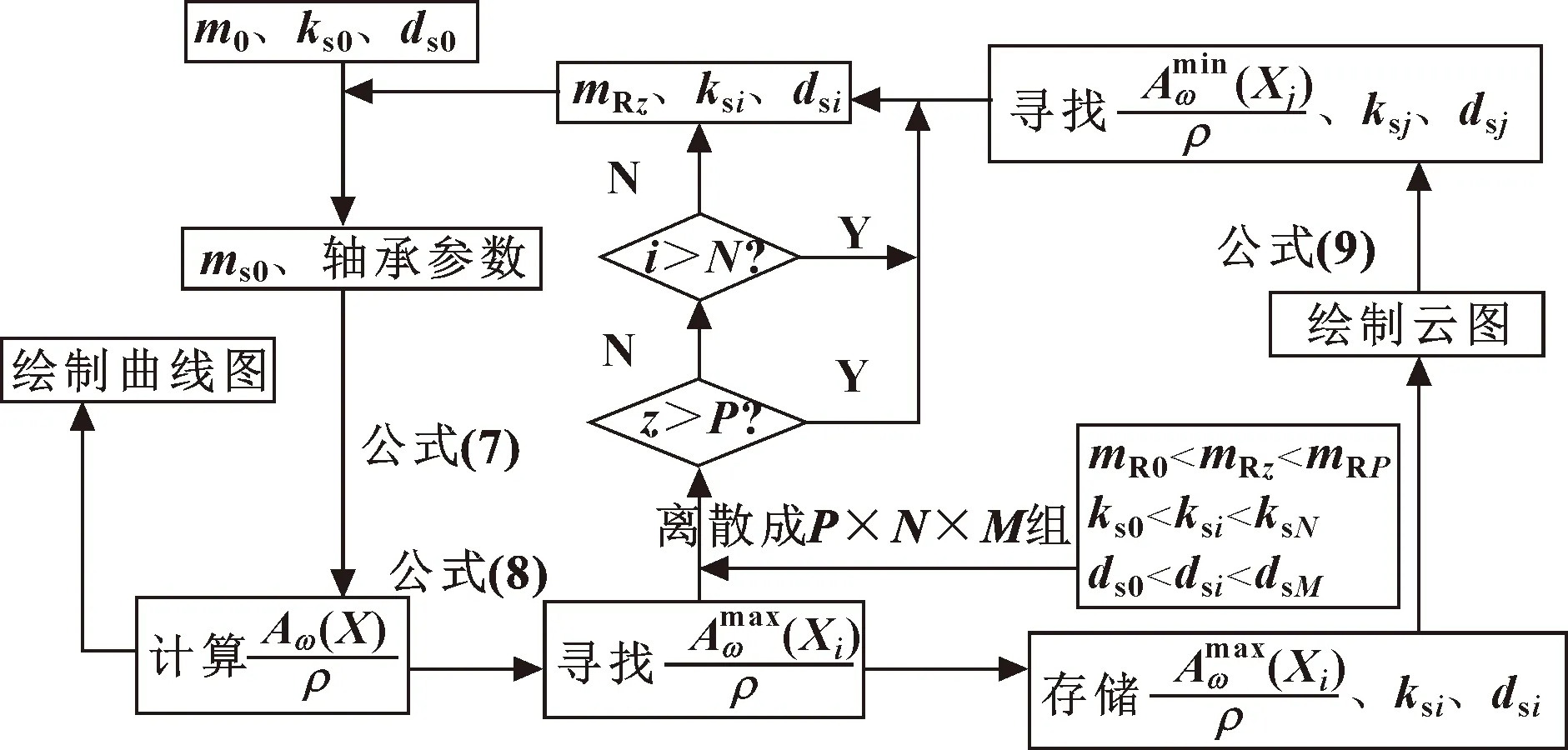
圖2 全局匹配分析方法示意

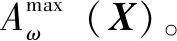
(8)

本文作者將合理范圍內的轉子質量、支承剛度及阻尼離散成××組動力學參數并計算出匹配點集后排列組合，構成系統支承參數的一個復雜的多維匹配空間，如圖3所示。

圖3 剛度-阻尼-振幅曲面示意

這是支承剛度和阻尼所組成的平面中計算出來的振幅比值在三維空間中構成的一個復雜曲面，而在這個復雜曲面中可能出現多個極值點，可通過式(7)尋找最小振幅比值，然后使用公式(9)來尋找最優匹配參數。

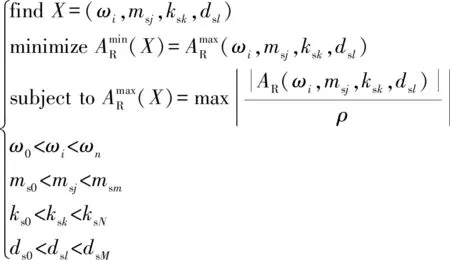
(9)

3 動力學參數全局最優匹配數值分析軟件系統

本文作者利用計算機高效的計算特點，在“支承參數最佳匹配與振動控制軟件” PASA-OSP的基礎上進一步架構設計和優化編程，實現了動力學參數全局最佳匹配數值計算軟件系統。通過輸入評估范圍內的剛度、阻尼、質量、轉速、振幅及偏心率等參數就能夠計算出全局最優匹配的過臨界振幅值最小RSS支承剛度和阻尼，對數值計算結果進行分析，研究參數時變性對穩定性的影響規律，最終建立比較完善的全局最優匹配及穩定性評估方法，并可評價全局動力學參數匹配域及最優匹配軌跡等，其總體編程思路如圖4所示。由于篇幅有限，具體內容可參考文獻[13-14]。

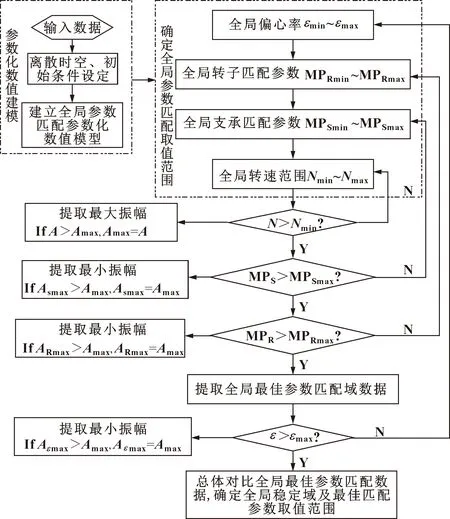
圖4 數值計算流程框圖

4 全局動力學參數最佳匹配分析

為了驗證軟件系統的可行性，以M701F燃氣輪機轉子系統參數(見表1)為例，研究轉子質量和剛度對系統最佳匹配的影響。

表1 轉子和RSS機座參數

根據簡化的Jeffcott轉子，通過改變轉子結構及質量，理論計算轉子剛度，分析轉子質量與轉子剛度的變化關系，將轉子質量的計算變化范圍設定為10～10kg，其轉子剛度全局變化范圍為2.15×10～1.63×10N/m。根據對數坐標均勻離散為200個點進行逐一計算，分析研究轉子參數變化對支承參數最優匹配的影響規律。

圖5表示在偏心率為0.125時，并保持其他參數不變的條件下，隨著轉子質量及剛度變化，最佳匹配支承剛度和阻尼的變化規律。由圖5可知，當轉子質量從1.0×10kg增加到8.26×10kg時，所對應的最佳匹配支承剛度從1.41×10N/m降低到1.04×10N/m，支承阻尼從1.06×10N·s/m增加到2.51×10N·s/m，但其支承剛度變化曲線呈階梯狀下降，即在局部轉子質量變化情況下其值保持不變，而支承阻尼則是成鋸齒狀曲線增長，即在對應局部轉子質量變化情況下其值增加，但到下一階段其值先下降后增加。

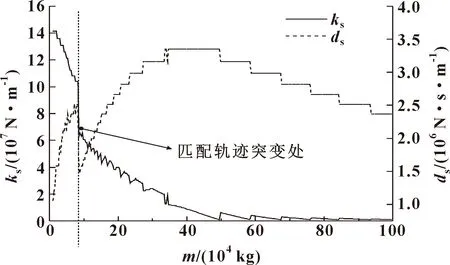
圖5 支承參數最佳匹配點的變化規律

當轉子質量由8.26×10kg增加到8.59×10kg時，如圖5所示，最佳匹配剛度從1.04×10N/m突變到6.3×10N/m，最佳匹配阻尼也從2.51×10N·s/m突變到1.49×10N·s/m，顯示出強烈的間斷性和不連續性。且突變后最佳匹配的支承剛度及阻尼變化趨勢出現交替變化。突變處的匹配云圖如圖6所示。

圖6 支承剛度、阻尼與振幅比全局云圖與最佳匹配點

圖6中所示的白圓圈點表示最小振幅出現的位置，也是RSS支承參數最佳的匹配點。從圖6(a)可以看出：當轉子剛度大于1.75×10N/m時最佳匹配點從封閉狹窄的三角域內的點突變到點，然后隨著轉子剛度逐漸增加形成新的匹配區域。

隨著轉子質量繼續增加至9.97×10kg，最佳匹配支承剛度在6.3×10N/m到1.04×10N/m區間內開始呈鋸齒形下降，而最佳匹配支承阻尼從1.49×10N·s/m到2.37×10N·s/m區間內呈階梯狀上升。

結合圖7為控制振幅比小于1.2時，最佳振幅比與轉子剛度和支承剛度的變化關系，可以看出：當轉子剛度為4.4×10～1.66×10N/m;支承剛度變化范圍控制在1.04×10～3.55×10N/m，可使振幅比小于1.1。而M701F燃氣輪機轉子系統的轉子剛度及支承剛度均處于這個范圍。

圖7 最佳匹配支承剛度下的轉子剛度和

以上分析可以看出：當偏心率為0.125，轉子參數變化，保持其他參數不變的條件下，最佳匹配點軌跡在轉子剛度1.75×10N/m附近呈現出奇異性，而奇異區域前后的支承剛度及阻尼變化趨勢恰好相反，且M701F燃氣輪機轉子系統的轉子剛度及支承剛度處于最佳匹配范圍，驗證了系統的可靠性與可行性。

5 結論

(1)通過全局匹配分析方法，建立動力學參數全局最優匹配數值分析軟件系統，研究基于M701F燃氣輪機轉子系統參數的數值分析，只需輸入轉子、支承機座和軸承的關鍵參數，就可高效快速地進行最優匹配數值分析和非線性振動分析。

(2)通過在全局轉子質量、剛度和支承剛度、阻尼范圍內進行數值計算分析可知：當偏心率等于0.125，穩定的轉子剛度可在4.4×10～1.66×10N/m的范圍選擇最優，支承剛度變化范圍控制在1.04×10～3.55×10N/m，這樣可保證過臨界振幅比不超過1.1的支承參數最優匹配。