多邊矩陣的塊拉長Te運算
羅 純,馬萱航,夏琪祺,郟君樂,潘 翔,張應山
(1. 上海應用技術大學 理學院, 上海201418;2. 硅湖職業技術學院 校長室, 江蘇 昆山215332;3. 華東師范大學 金融與統計學院, 上海200241)
象數學邏輯[1]主要研究對象為多個復雜系統并探究其內部存在的某種運算關系,復雜系統包含2部分,根據變量為輸出變量或輸入變量對空間給出定義,輸出變量構成的空間定義為象空間,輸入變量構成的空間定義為卦空間。在對象空間內數據存在的客觀規律研究的過程中,結論是可逆數據的變換分析結論是具有再現性的。在一般的矩陣中,矩陣按行拉長vecr運算和按列拉長vecc運算也被定義為常用的運算法則。推廣到多邊矩陣理論中,這2個運算也形成多邊矩陣理論的基本運算之一,定義為塊拉長Tensor運算,分別用Te、te表示。
文獻[2-3]中主要探究了不同指標問題的運算規律和相關性質,并給出其從特殊情況推廣至一般場合的證明;文獻[4-5]中分別利用多邊矩陣的基陣和置換矩陣探究了在多邊矩陣中存在的一些一般運算法則,文獻[6-9]中的按行拉長Vr=vecr和按列拉長Vc=vecc及 其相應的逆的運算方法,也可以歸納為是多邊矩陣塊拉長Te及其逆Te-1運算規則的一種特殊情況,即總體拉長te及其逆te-1運算的情況。而本文則是為了將一般矩陣按行拉長vecr的運算法則和性質推廣至多邊矩陣,并探究多邊矩陣塊拉長Tensor運算規則。
1 多邊矩陣塊拉長Tensor 運算的定義和基本定理
定義1.1設多邊矩陣的一個剖面可以表示為
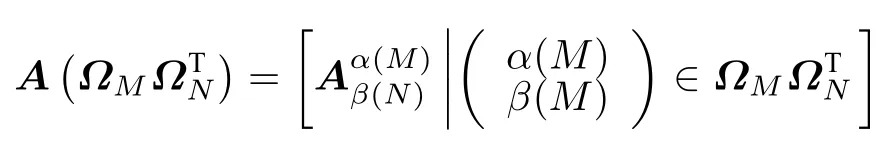

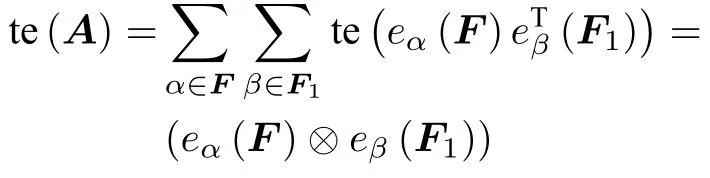
稱te(A)是多邊矩陣A的總體拉長,其中為基陣總體拉長te的 基本拉長定義。其他拉長同理可得。
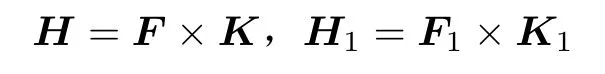
令eα(F)、eβ(F1)、eλ(K)、eμ(K1)分別為F、F1、K、K1型多邊矩陣的標準基陣。
記IF、IF1、IK、IK1分別為F FT、、KKT、型單位多邊矩陣。又記分別為F(F×K)T、型多邊矩陣。又記HKT多邊矩陣為
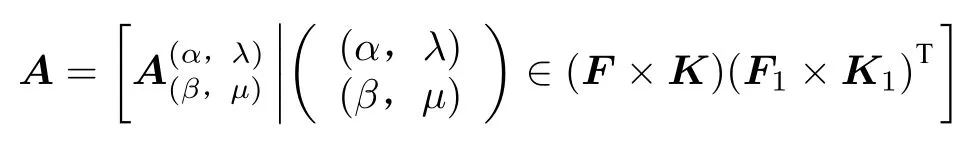
則
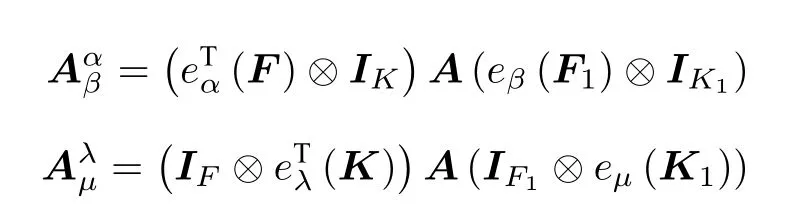
定理1.1如果設矩陣A的一個剖面表示為,那么如下結論是等價的。
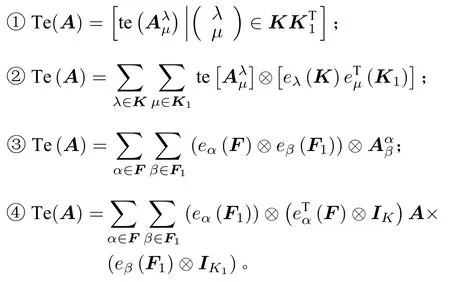
證由定義1.1可知等式①和②是等價的。等式③和④表達了同一個等式,因此它們是等價的。
只需證明等式②和等式③是等價的即可。
根據多邊矩陣A的定義可知,多邊矩陣A沿框架的基陣為
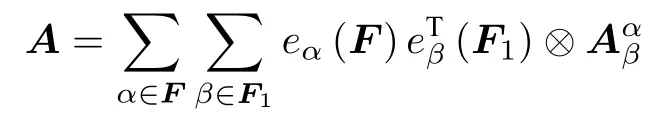
而多邊矩陣A沿框架的基陣表示是
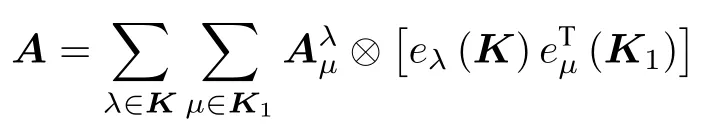
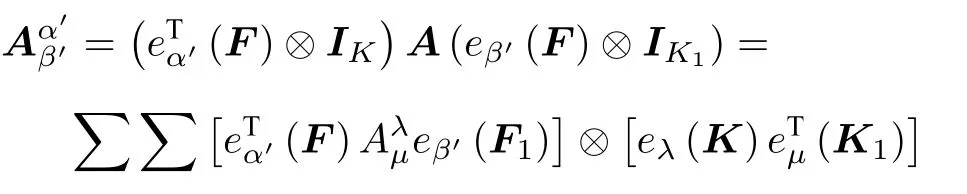
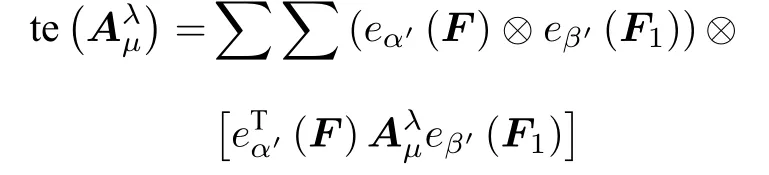
可知
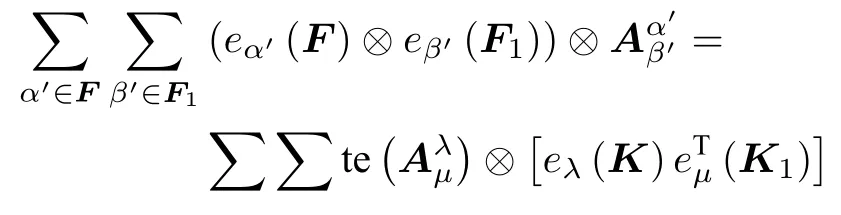
這說明等式③和等式②是等價的。即證。
推論1.1若A為型多邊矩陣,則A沿框架的塊拉長為
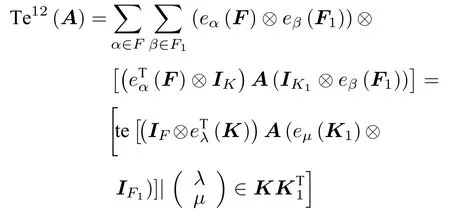
若A為型多邊矩陣,那么沿A框架的 塊拉長為
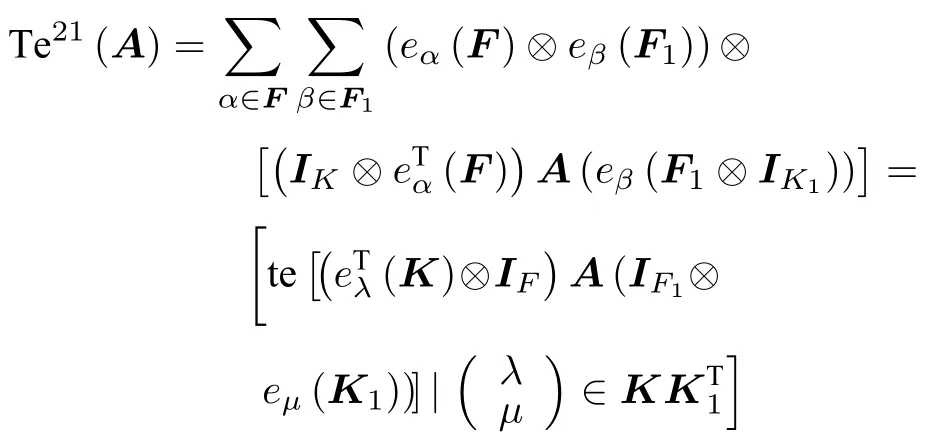
若A為型多邊矩陣,那么A沿框架的塊拉長為
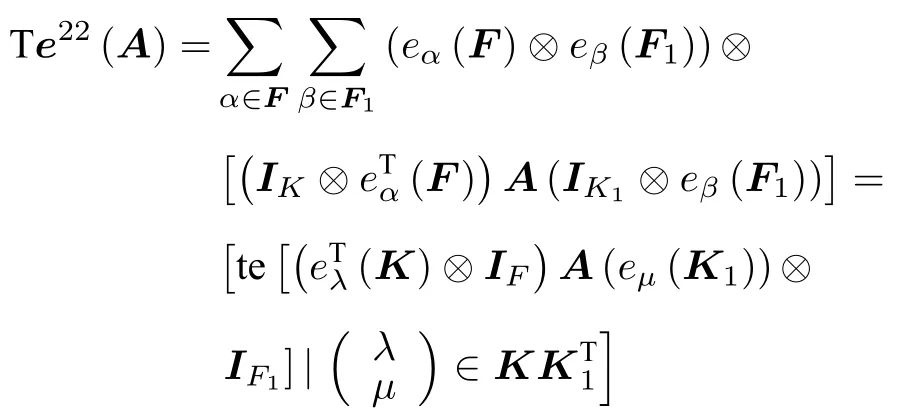
2 多邊矩陣塊拉長Te 的基本性質
性質2.1(線性與轉置)如果A,B為×型多邊矩陣,a、b為數值,*T定義為多邊矩陣轉置,則
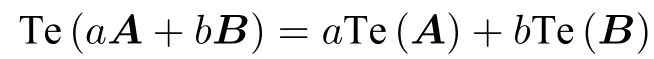
設多邊矩陣A沿剖面的基陣表達性質為
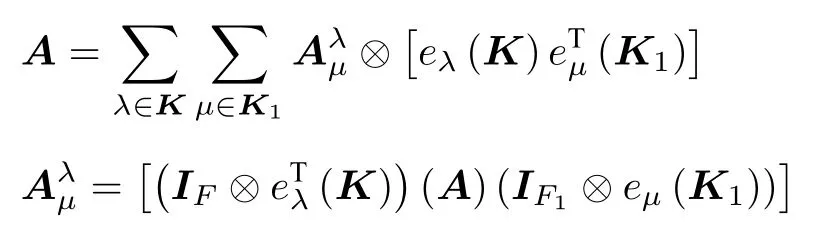
記塊轉置T (A)為:
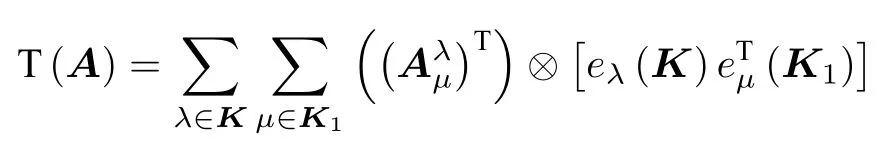
則
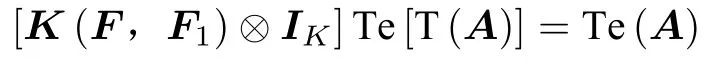
其中
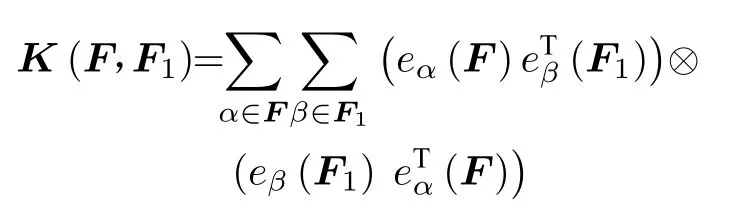
為換位多邊矩陣。
證明用定理1.1的結論4可知
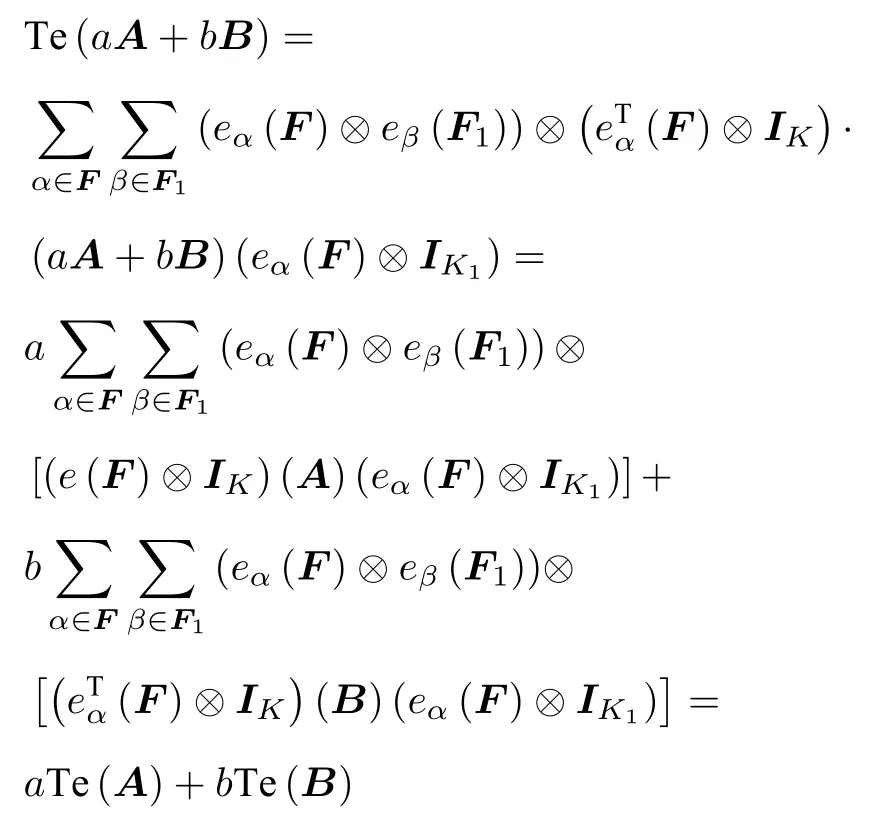
因為
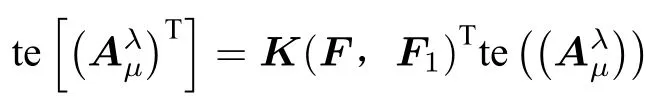
所以
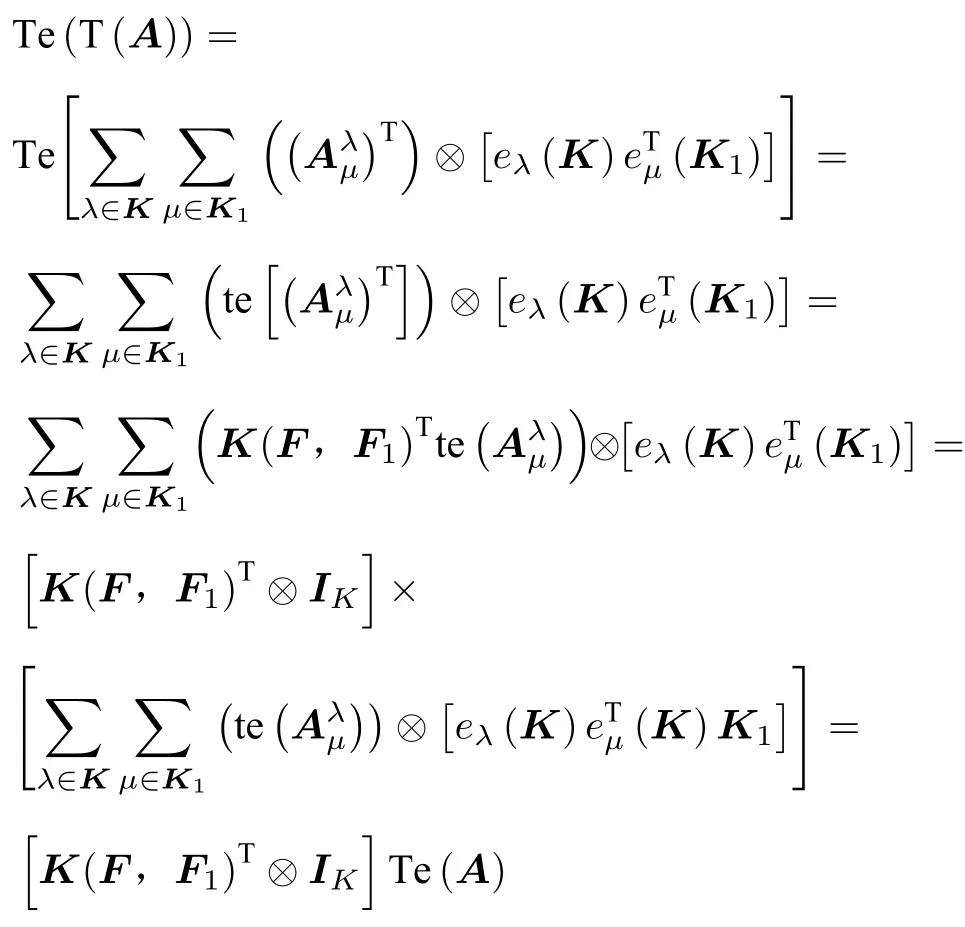
即證。
性質2.2(Kronecker積性質)如果A、B分別為型多邊矩陣,則
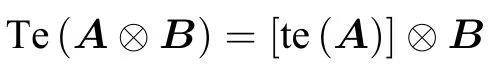
證根據定理1.1已知,,,可以得到
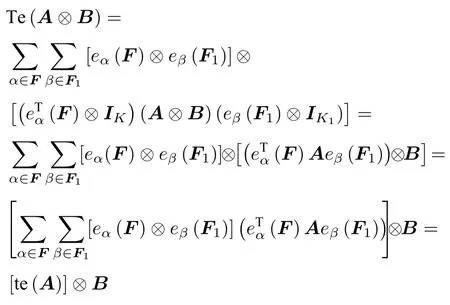
即證。
性質2.3(乘積性質)如果A為型多邊矩陣,C為K0KT型多邊矩陣,D為型多邊矩陣,則
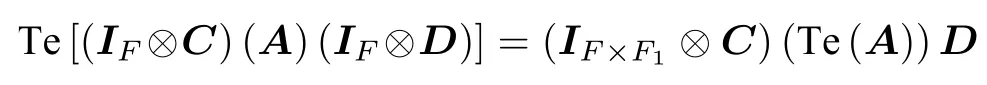
證根據定理1.1已知,
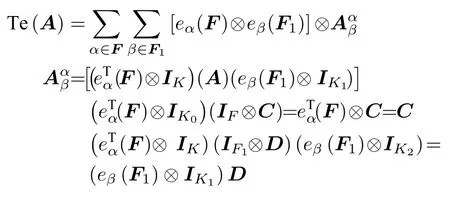
可以得到:
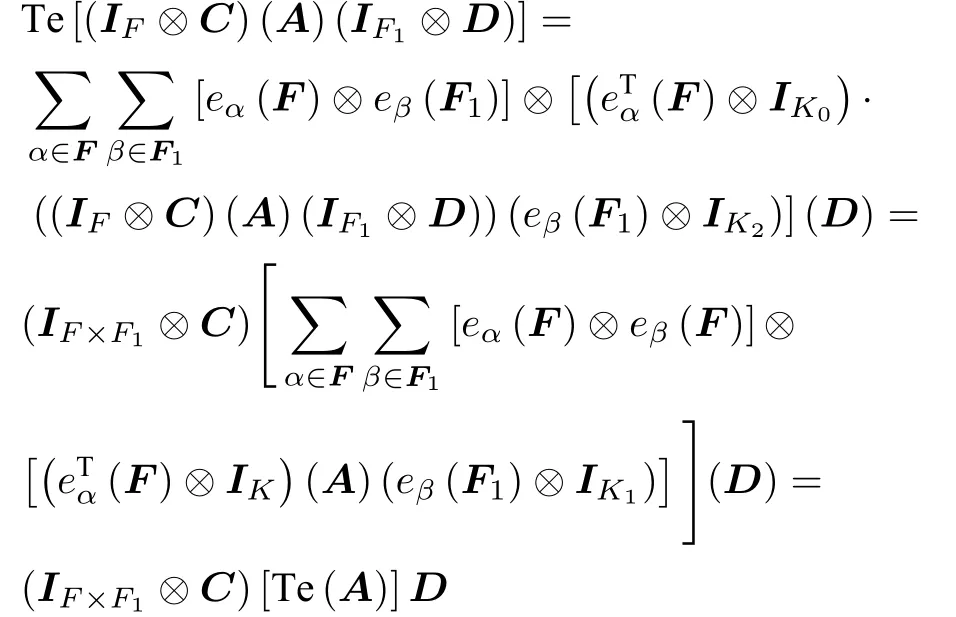
即證。
性質2.4(乘法拉長)如果A為型多邊矩陣,C為F0FT型多邊矩陣,D為型多邊矩陣,則
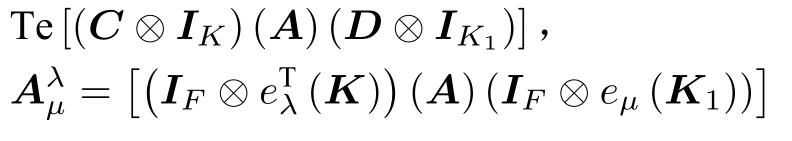
證根據性質2.1已知,
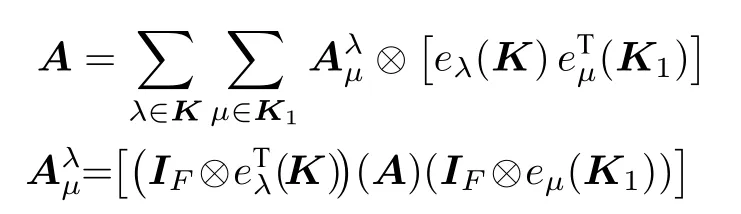
根據定理1.1已知,
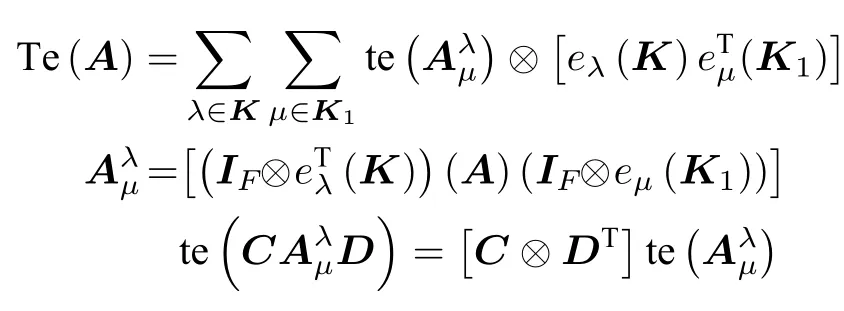
可以得到:
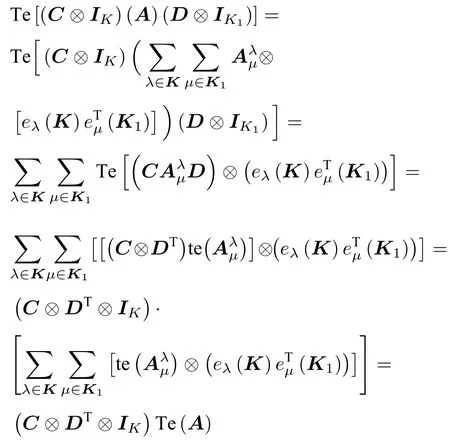
即證。
3 塊拉長Teij 之間的關系
定義3.1如果A為型多邊矩陣,多邊矩陣A沿剖面的基陣表達性質為
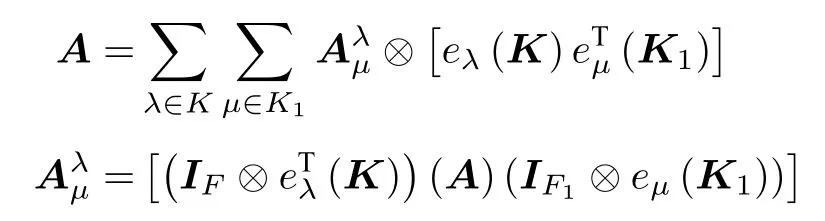
那么定義運算記號te?IK為

Te=Te11=te?IK
則。
如果A為型多邊矩陣,多邊矩陣A沿剖面的基陣表達性質為
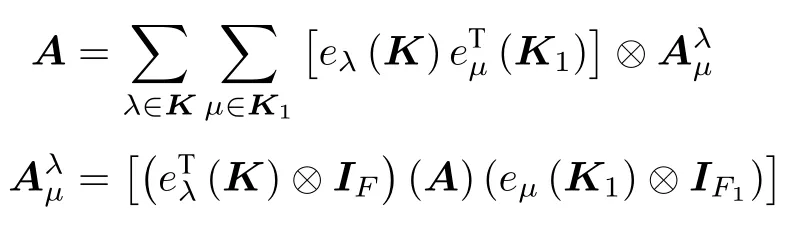
那么定義記號IK?te為
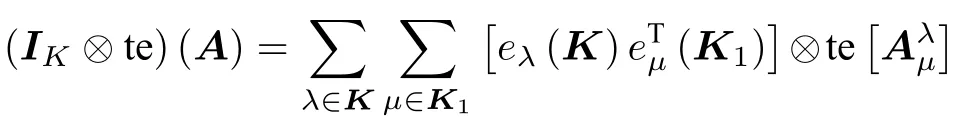
如果A為型多邊矩陣,多邊矩陣A沿剖面的基陣表達性質為
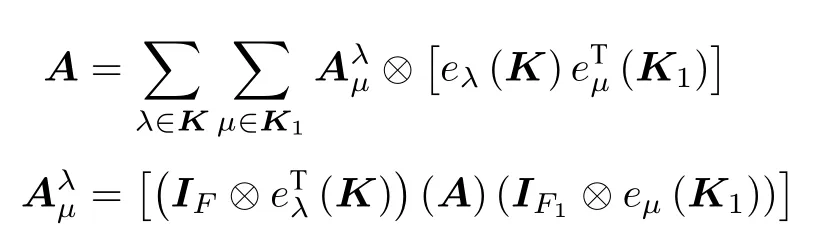
那么定義記號te?te 為
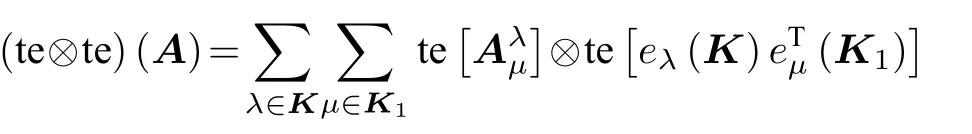
則te=te?te, 定義為總體拉長。
性質3.1(塊拉長的嵌套性質)如果A為型多邊矩陣,Te(A)=Te11(A)為多邊矩陣A沿框架的 塊拉長,te(A)為A沿框架的總體拉長,(IF?te)(T(A))為Te(A)=Te11(A)沿框架的塊拉長,則
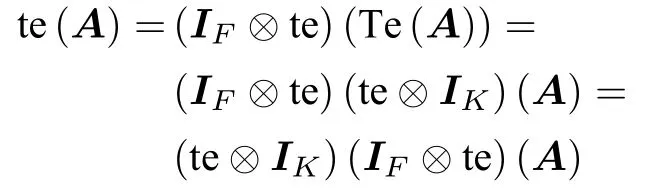
其中, Te11=Te 。
證根據定理1.1和多邊矩陣的基陣表達性質可知,
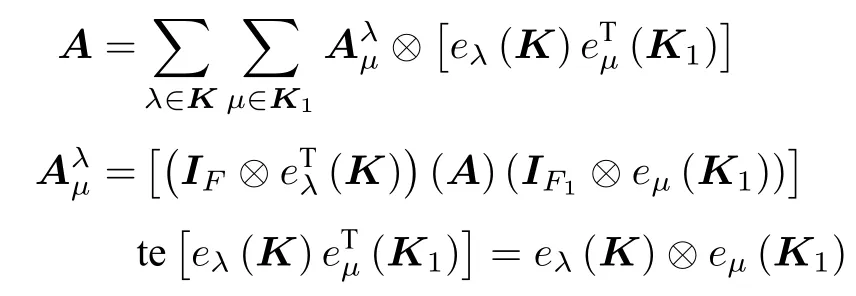
根據總體拉長的定義可知,
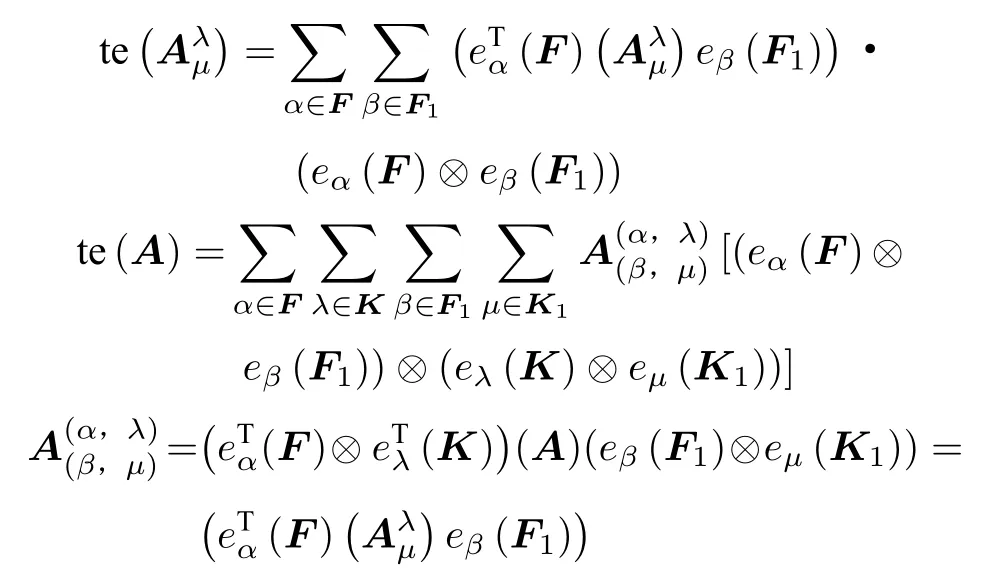
可以得到:
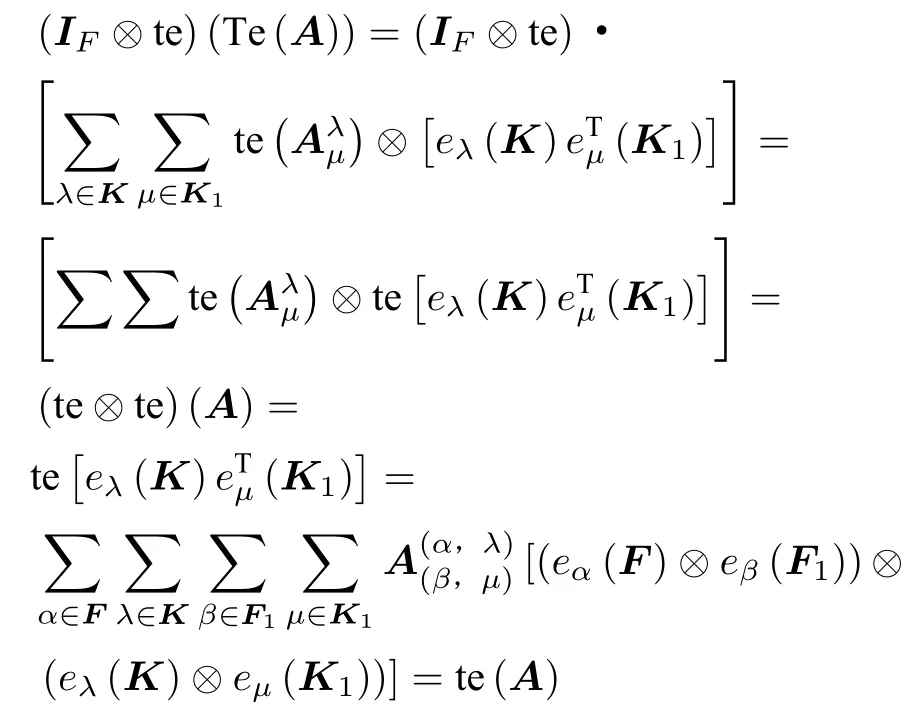
因為te?te與的乘法位置無關,所以

即證。
性質3.2(多邊矩陣塊拉長Te和塊拉長Teij的關系)
(1) 如果A為型多邊矩陣,那么AK(F1,K1)T為型多邊矩陣,K(K,F)A為型多邊矩陣,則
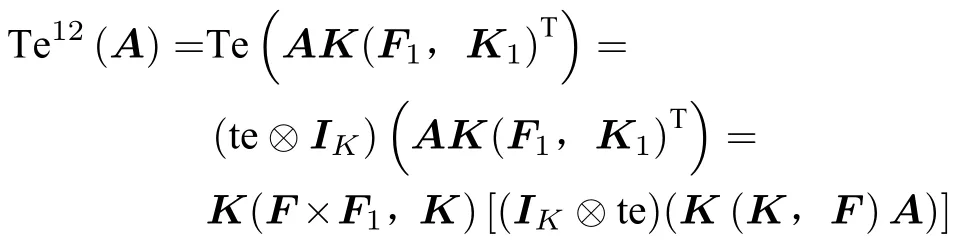
(2) 如果A為型多邊矩陣,那么K(F,K)A為型多邊矩陣,AK(K1,F1)T為型多邊矩陣,則
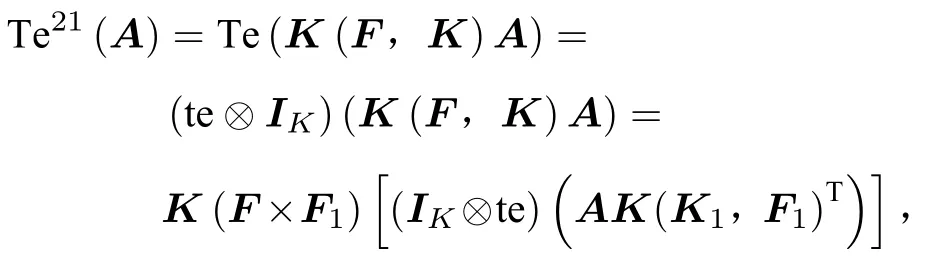
(3) 如果A為型多邊矩陣,那么K(F,K)AK(F1,K1)T為型多邊矩陣,則
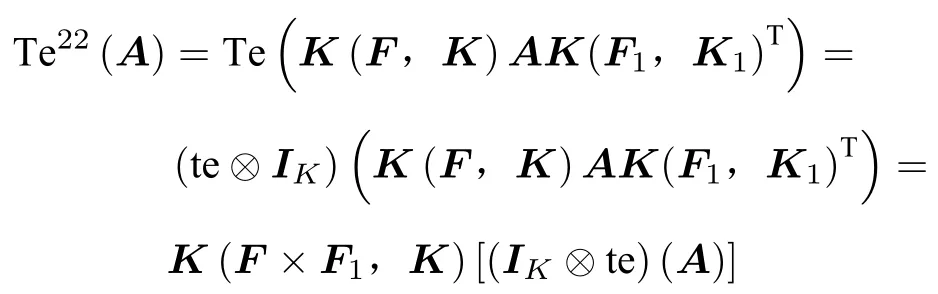
其為型多邊矩陣。
(4) 如果A為型多邊矩陣,那么(A)T是型多邊矩陣,則,
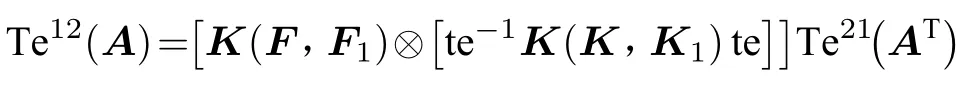
證(1)先證結論3根據推論1.1,如果A為型多邊矩陣,那么多邊矩陣A沿剖面的基陣表達性質為
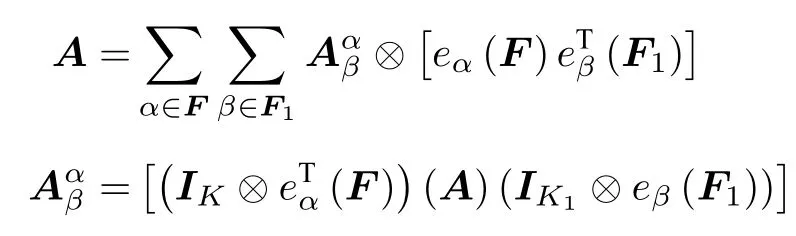
于是,采用記號(IK×te)滿足
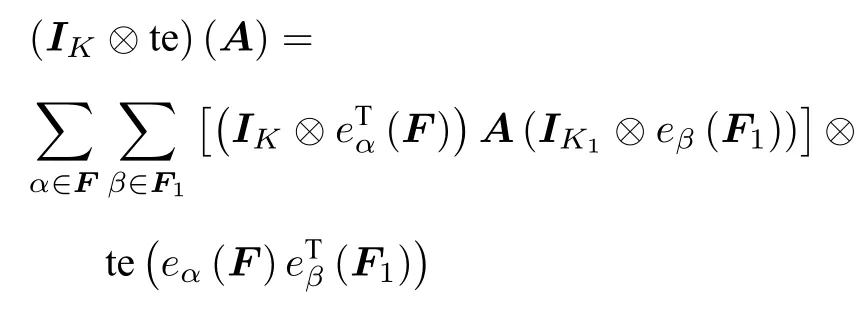

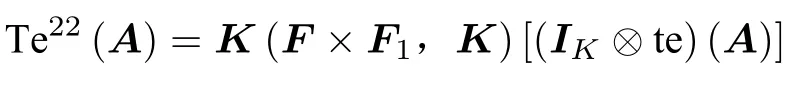
于是得到命題的結論3的最后等式。其他等式是定義。
證(2)根據上述結論3可知
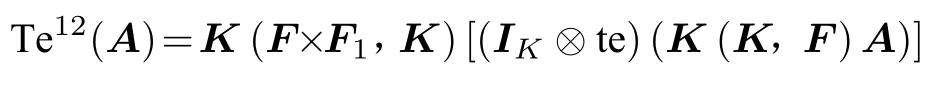
于是得到命題的結論1的最后等式。其他等式是定義。
證(3)根據上述結論3可知
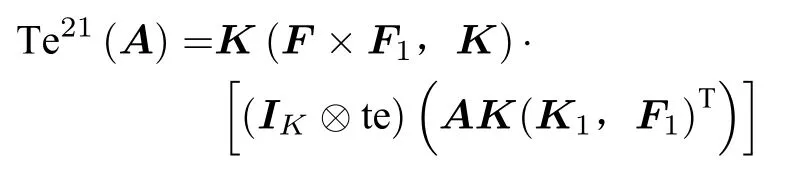
于是得到命題的結論2的最后等式。其他等式是定義。
證(4) 如果A為型多邊矩陣,則(A)T是K1FT×F1KT型多邊矩陣,用結論1和2知,
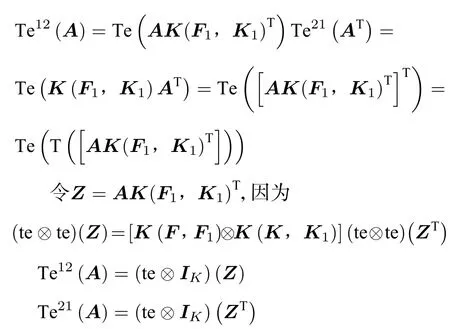
所以
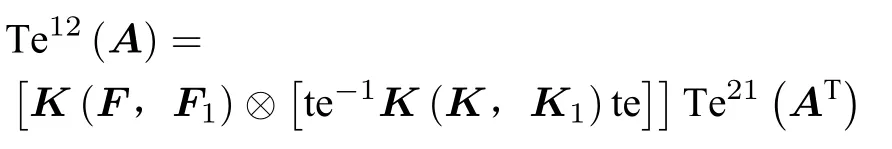
即證。
4 結 語
本文的推導過程嚴格證明了多邊矩陣的塊拉長Te和塊跡Tr存在著密切關系;也與總體拉長te和總體跡tr關系密切,即Te=te?IK和Tr=tr?IK。而總體拉長te與運算te?te運算有關,總體跡tr與運算tr?tr運算有關。塊拉長Teij基本是等價的拉長運算,與記號IK?te具有關系。各種運算之間僅僅相差置換多邊矩陣,說明各種塊拉長Tensor運算都是可逆的等價運算,具有同構運算性質,是考慮再現性問題的重要運算工具。

