多品種小批量生產模式下共軛貝葉斯動態質量控制方法

李曉波，孫小慧

（新疆大學 建筑工程學院，烏魯木齊 830017）

對于制造業而言，產品質量是企業重要關注的議題之一，也是影響企業利潤率的重要因素。通過對生產各個階段進行過程控制可以發現制造過程中存在的異常情況并進行分析，給出相應的解決辦法和措施，完成質量控制和提升。

隨著全球經濟的快速發展，市場經濟的需要也在不斷地變化，多品種、小批量的生產模式也在逐步演化成現在最主要的生產模式。目前，多品種、小批量生產方式下工序質量控制主要有4種方法：精確控制界限法、成組技術法、統計變換法和貝葉斯估計法。

20世紀50年代King[1]第一次提出精確控制界限法，此法以小樣本數據量為基礎設置精確控制界限，控制限下的每個質量數組誤報錯誤的概率持續在較小的值。該方法局限于控制圖中的控制限隨著樣本容量的調整而變化，對樣本容量的變化很敏銳，容易忽視漏發報警。為了解決精確控制界限法漏發報警的缺陷，國內外學者以成組技術中的相似性理論為依據，通過充實樣本容量解決過程質量控制中數據量較少的問題[2]。Desmond[3]針對多品種、小批量數據缺少問題，提出工序質量控制一個工序中其他相似零件可以提供質量信息的想法從而擴充質量數據庫，為實現精確質量控制提供關鍵理論方法。楊旭等[4]對成組技術中的相似工序法進行研究，認為生產過程中各工序之間是相似的，同時影響工序質量的各因素也是相似的并存在密切相關性，同時給出了計算相似度的方法。

成組技術雖然解決了質量控制中數據量較少的問題，但不同產品、不同批次的質量數據相關性和不是同一分布的問題，給數據分析工作帶來阻礙。為了滿足不同產品獨立同一分布，同時也為了消除不同生產過程中不同均值和不同公差帶來的不利影響，國外學者Quesenberry[5]提出通過統計變換解決過程質量控制中數據統計問題，該方法為了實現不同母體數據采用相同統計方法處理，引入標準正態數據變換將數據正態化來完成。余忠華等[6]將成組技術中相似元理論與統計變換過程控制方法相結合，提出了通過相似元分析和統計變換來構建相似工序，實現生產過程中質量的有效控制，該方法局限于需要相關產品技術支持，且收集的數據一般可能為非正態分布。

當統計的生產過程質量數據服從非正態分布時，國內外學者提出了以貝葉斯估計為基礎的統計控制方法，該方法將生產過程中的歷史數據與人們的主觀評價、預測和判斷相結合，通過控制圖和過程能力分析建立實時跟蹤與預警的生產質量控制模型，從而在低樣本容量下實現高精度預測。卡祥民等[7]以貝葉斯分析為理論基礎，將先驗和樣本信息相結合用貝葉斯理論估計當前產品質量數據的分布參數及回歸系數，并根據所得參數繪制相關控制圖，實現對小批量生產的質量管理。該方法在生產過程變動不大的產品過程質量控制中得以應用，當此方法遇到生產過程變化大時，如生產品種較多，批量小，加工工序復雜，會因無法獲得足夠多歷史樣本數據而無法使用。趙飛濤[8]對多品種、小批量生產模式進行研究，提出通過共軛貝葉斯估計完成統計過程控制模型的建模，在當前少量容量下有效地估計2個或2個以上未知參數，有效規避以往貝葉斯估計在估計2個或2個以上未知參數的局限性。但該方法未考慮先驗信息中歷史批次質量數據的加工時間與當前批次的加工時間的相關關系，即先驗信息中歷史批次質量數據的加工時間與當前批次質量數據的加工時間越靠近越能反映當前的生產狀況，如不考慮此種情況會引起統計過程控制活動的無效或引起嚴重的質量問題，所以在研究中各先驗信息權重占比需考慮進去。

針對多品種、小批次生產模式國內外研究的局限性，本文引入共軛貝葉斯理論，實現及時追蹤和反饋的工序質量控制目的。首先根據成組技術中的相似理論選擇備選先驗信息，通過統計變換方法將歷史數據進行變換處理，經過里爾福斯（Lilliefors）檢驗、聯合假設檢驗（F檢驗）確定為先驗信息；然后以時間序列指數加權理論對歷史數據各批次賦予權重；其次通過共軛貝葉斯方法完成工序質量控制模型的建立，在產品質量數據累計過程中計算控制限，實現工序質量控制的及時追蹤與預警；最后通過實際案例利用MATLAB工具比較此種方法與常規方法的優缺點。上文提出的共軛貝葉斯統計控制方法流程如圖1所示。

圖1 共軛貝葉斯工序質量控制方法流程圖

1 先驗信息的確定

產品工序質量控制的第一步就是收集一段時間段內與相似理論相符的歷史質量特征數據，然后以數據變換的方式將各批次相關數據轉換為具有同分布的情況，其次對變換后的歷史質量數據做方差和均值的齊性檢驗，最后將檢驗合格的歷史質量數據作為共軛貝葉斯建模的先驗信息。

1.1 成組技術

運用成組技術，首先就是要利用工序相似性分類方法對工序相似性研判。企業根據現場實際情況選取相應方法，如目測分類法等，將生產中的影響工序質量的5M1E，即人、機器、材料、方法、環境和測量5個因素，通過篩選、分類匯總，構建工序相似性評定模型，通過以上模型收集相關重要工序同組內的歷史批次質量數據，將其作為備選先驗信息。

1.2 數據變換

由于各部件的基本尺寸和公差值的差異，導致了其歷史批次質量數據平均值μ和方差δ的差異，因此，必須對不同零件的歷史批次質量數據進行規范化，實現相似工序質量特征數據的同一分布。數據處理流程如下

式中：yij為標準化數據；xij為j批樣本中的第i個樣本實測數據；Mj為第j批樣本的公差中心；Tj為第j批樣本的公差，Tj=TUj-TL。

式中：TUj為第j批數據的上偏差；TLj為第j批數據的下偏差。

1.3 先驗信息篩選

用Lilliefors檢驗對待選的m批先驗樣本信息進行篩選[9]，方法如下。從m批樣本中隨機抽取第j批樣本xj進行檢驗，原假設為xj服從正態分布，Lilliefors檢驗的檢驗統計量為

式中：sup為集合中的最大值；G（yj）為第j批樣本累計分布函數；F（yj）為以第j批樣本均值和方差為總體均值和方差的累計分布函數。樣本均值和方差依據式（4）執行。

當D檢驗統計量小于等于標準值時，原假設成立，即該樣本特征服從正態分布。

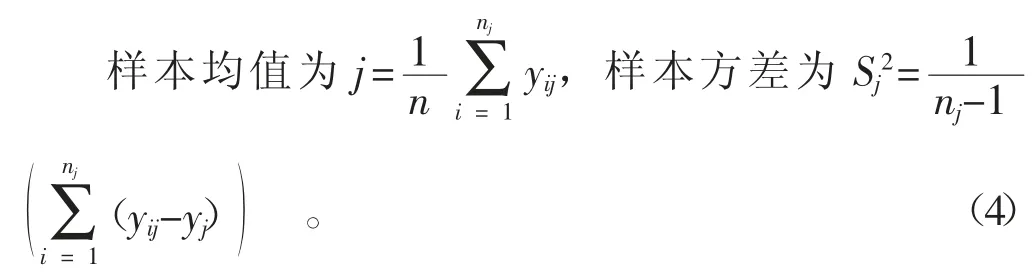
為了保證備選數據與當前樣本數據方差的一致性，需先利用Bartlett's球狀檢驗[10]進行判別，Bartlett's球狀檢驗的原假設H0為所有的樣本總體即m+1批數據的方差σj2是否相等。樣本容量為nj的（m+1）批樣本中，用第m+1批樣本方差Sj2代替第j批樣本的總體方差σj2估計值，Bartlett's球狀檢驗統計量為

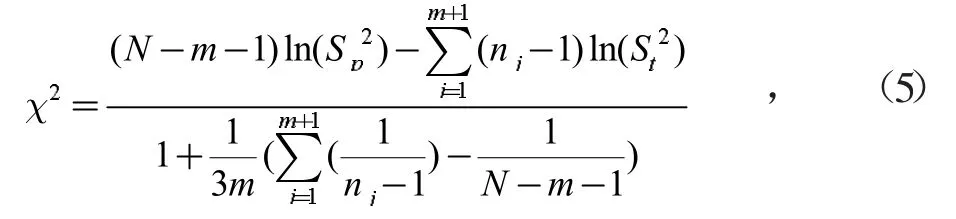
為了保證備選數據與當前樣本數據均值的一致性，確保共軛貝葉斯估計中先驗和后驗分布總體均值一致。需采用單因素方差分析確定備選數據與當前樣本均值是否相同。即采用F檢驗

當F＞Fa（r，N-r-1）時，備選信息中各批次樣本組的總體均值不同，且Fa（r，N-r-1）為F的臨界值不能作為先驗信息，還需對剩余備選信息中的樣本組重新進行F檢驗，直至出現F＜Fa（r，N-r-1），最終得到m批的歷史數據，將其做為可選的先驗數據。

2 共軛貝葉斯質量控制模型建立

2.1 控制圖的建立

產品的好壞有一定的隨機性，產品質量特征值可以反映質量的好壞程度，把這種隨機性分布通過建立產品質量控制模型進行監控，一般認為質量控制模型建立在正態分布連續隨機變量的基礎上，而產品的質量特征值落入（μ-3σ，μ+3σ）的概率為99.7%。由此確定產品特征值的控制圖：CL為中限，UCL為上控制限，LCL為下控制限。

由公式（7）可知，質量控制的效果主要取決于對質量數據均值μ和方差σ的準確估計，利用共軛貝葉斯控制模型可以充分利用先驗信息提高參數μ、σ估計準確率，從而實現對質量的有效控制。

2.2 共軛貝葉斯參數的估計

2.2.1 先驗信息均值、方差計算及權重分配

通過數據變換、篩選后歷史數據得到（y1，y2，y3，y4，…，ym）=Y組先驗數據，且服從正態分布N（μ，σ2），則各歷史數據為yij=N（μj，σj2）。

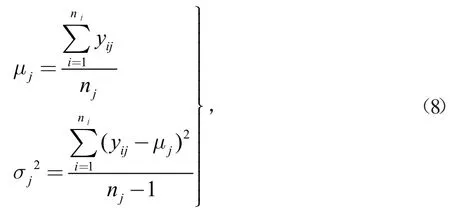
式中：nj為第j批歷史數據樣本容量n。

企業在生產過程中，加工時間與當前生產批次靠近的歷史數據，應該與當前生產情況有更緊密的聯系。由此可以根據時間序列中的指數加權思想為各批次歷史數據進行賦權值。

根據多品種、小批量生產模式自身特點，因企業檢驗方式的不同，可能造成各批次所選取的歷史數據的數量也有可能不同，為此可通過變樣本容量計算公式獲得各歷史數據間的均值和方差。

將指數加權思想和多品種、小批量生產模式下變樣本容量計算公式相結合，可得歷史的質量數據的組間均值和方差為

2.2.2 μ，σ2參數估計

根據貝葉斯理論中多參數模型，若先驗信息已知，總體方差σ2未知，總體方差服從逆伽馬分布（IGa），即σ2的先驗分布為逆伽馬分布，記為IGa（α，β），μ的先驗分布為正態分布，考慮到μ和σ2間有相互影響，故其共軛先驗分布有乘積形式π（μ|σ2）π（σ2），可以表示為μ|σ2~N（a，b2）；σ2~IGa（α，β）。μ，σ2分布參數依據先驗數據計算可得，計算方法如下。

（1）σ2的估計，因σ2~IGa（α，β），根據逆伽馬分布的性質，可得

聯合（10）和（11）可得

在獲得當前數據Y后，當目前樣本σ2服從逆伽馬分布，由共軛貝葉斯理論可知，其后驗與先驗分布形式相同，可記作

由此可得σ2的貝葉斯估計

（2）μ的估計，因μ|σ2~N（a，b2），根據正態分布性質可得μ期望值

在獲得當前批次樣本數據Y后，由共軛分布性質可得

因聯合先驗分布為π（μ，σ2）=π（μ|σ2）π（σ2），由此可得，聯合后驗分布π（μ，σ2|Y）可得條件后驗密度π（μ|σ2，Y）和邊緣后驗密度π（μ|Y）的乘積，將聯合后 驗密度σ2積分，可得μ的邊緣后驗密度

利用逆伽馬分布密度函數的正則性性質，得出

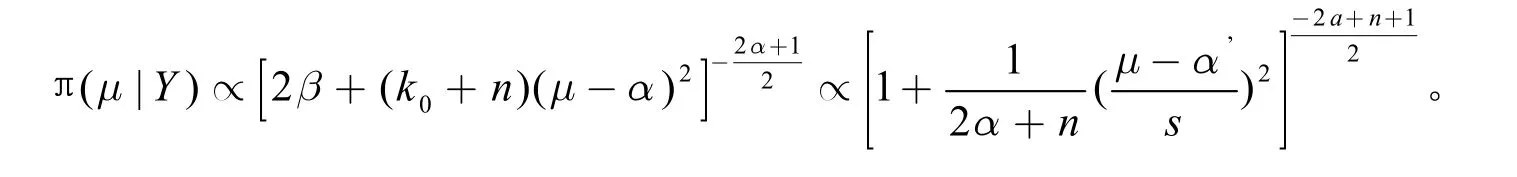
這是個自由度為（2α+n）的t分布，其中

由此可得μ的貝葉斯估計為

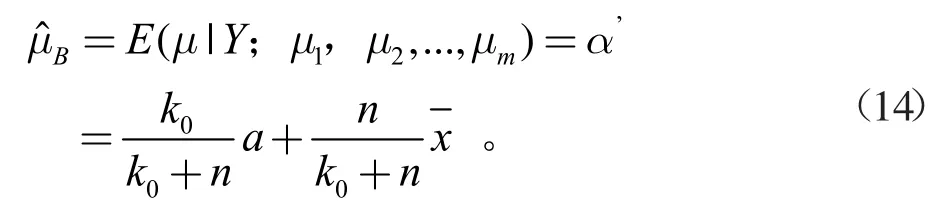
（3）計算控制限。依據多品種、小批量生產模式下質量數據的特點，選用單值-移動極差控制圖，同時結合生產過程中實際數據，根據式（13）、式（14）計算α，β貝葉斯估計值，求控制圖控制限

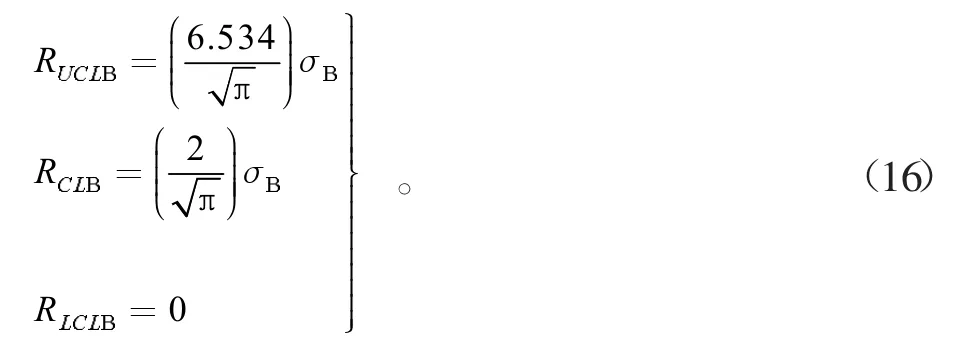
移動極差控制限為

依據統計學的原理，得移動極差控制限計算公式可以轉化為

2.2.3 工序過程能力

在生產中，工序能力是否滿足要求計算公式如下

式中：CP為工序能力指數表示過程均值與公差中心值重合時的狀態；CPK為工序能力指數過程均值與公差中心值有偏移的狀態；μl，σl分別為未變換前的原始數據的均值和標準差。

3 實例驗證

以某電機制造廠家總裝車間中的轉子導條漲緊工序為例，利用MATLAB仿真比較本文方法與現有常用最大似然估計方法的優劣。

表1 歷史質量特征數據

假設工序過程能力指數為1.67并進行仿真，由此可得，每批數據的標準差σij=Tj/6，均值為Mj。根據式（16）可得，總體分布的均值μ=0，標準差σ=σij，Tj=1/10，由此可根據正態分布（0，0.01）生成仿真數據。

本文采用的單值-移動極差控制圖的效果主要取決于對分布參數總體均值μ和總體方差σ的準確估計，故本文通過MATLAB生成數據與歷史數據相結合，比較本文方法與最大似然估計在總體均值μ和總體方差σ的估計情況，已確認本文方法的有效性。

具體仿真過程如下。

（1）根據正態分布（0，1/10）生成數據，然后從中取n個數據作為當前批次，n的初始值為1，計算當前樣本的均值μ和方差σ2。

（2）根據表1，從其中抽取10批數據，每批歷史數據確定為30個樣本。抽取的樣本數據經過式（1）變換后，先后進行Lilliefors、Bartlett's球狀、方差分析（ANOVA）檢驗確定選定的歷史數據與當前的數據是否來自同一分布，如是留存，不是棄之，直至生成樣本容量為30的10組歷史數據。

（3）將指數加權思想與各批次歷史數據進行指數加權結合，可得歷史數據的組間均值和方差。

（4）利用先驗歷史數據計算超參數μˉ，σˉ，α，β。

（5）利用當前數據信息結合超級參數通過貝葉斯模型得到貝葉斯參數估計的值。

（6）以傳統的方法最大似然估計得出當前樣本的參數值。

（7）計算樣本容量m下的平均絕對誤差

式中：xmn為仿真估計值；Ln為樣本容量n下真實值。

由圖1、圖2可知，當目前樣本量持續增大時，最大似然和共軛貝葉斯計算所得的分布參數估計的平均絕對誤差逐漸降低，但是當選擇樣本數量時以共軛貝葉斯估計為基礎的平均絕對誤差比最大似然估計要小得多。絕對誤差能夠反映估算值的準確度，而隨著誤差的持續變化，估算值的持續縮小和真實狀況也隨之接近。由此得出2個結果：一是在小樣本生產條件下，共軛貝葉斯估計更能反映實際情況；二是隨著樣本的增加，估算值的接近程度也隨之提高。

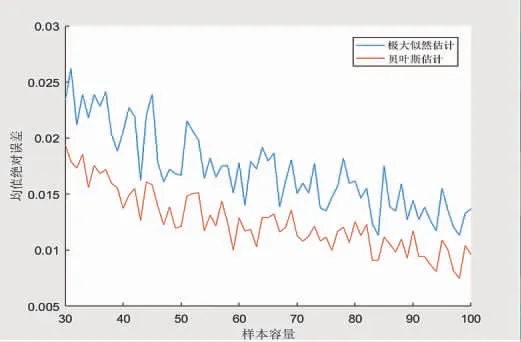
圖1 總體均值下2種估計方法的平均絕對誤差比較

圖2 總體方差下2種估計方法的方差絕對誤差比較

本文結合成組技術中相似理論同時利用數據變換方法，通過數據檢驗，將各批次歷史質量數據作為當前數據的有效補充，同時通過指數加權將各批次數賦予權重。利用共軛貝葉斯理論的優點，實現產品質量的及時追蹤和反饋。為了驗證本方法的有效性，本文通過仿真與現有傳統方法比較，本方法在適用范圍、控制效果等方面均有顯著效果，在多品種、小批量工序質量控制中能有效解決質量控制問題。因在生產過程中的觀測值呈現出自相關性，為此在后期工作中，需進一步對研究觀測數據相關性進行分析，實現此模型下多品種、小批量工序質量控制的有效性。