多效率擾動下復雜熱力系統能效分析與評價方法
陳海平, 薛凱麗, 張 衡
(華北電力大學 能源動力與機械工程學院, 北京 102206)
火力發電廠是能源消耗大戶,是復雜熱力系統的應用典范。實現復雜熱力系統的集成與優化,既是提高火力發電廠經濟效益的有效途徑,也是實現國家“雙碳目標[1]”的重要一環。因此,如何評價復雜熱力系統在多效率擾動模式下的能效水平,考察不同邊界條件下總系統的能耗分布及其影響權重,是一個亟待解決的關鍵問題。
對于1個由多個子系統或熱力設備構成的發電廠熱力系統(綜合系統),其總效率等于各分效率的連乘。眾所周知,機組實際運行過程中,綜合系統的效率擾動源可能是單一的,但多數情景下是多種效率擾動源同時存在的,即多個子系統或熱力設備的效率是同時改變和相互耦合的。值得注意的是,即使僅有單一擾動源,也可能引起多個熱力設備的效率發生變化。目前,關于多效率擾動源模式下綜合系統的能效分析與評價方法卻鮮有報道,相關研究主要集中在子系統或某些熱力設備運行能效和評價方法上,屬于局部優化的范疇[2]。楊勇平等[3]針對蒸汽朗肯循環和S-CO2布雷頓循環的典型流程,提出了一種熱力循環流程重構能效分析方法。張春發等[4]針對火電機組熱力系統的構成特點,從不同視角考察了主要運行參數和輔助汽水流量等因素對機組熱力系統運行熱經濟性的影響。閆順林[5]探究了多元擾動下汽輪機汽水動力循環運行能耗的時空分布及其耦合機制,獲得機組在多元擾動下的能效指標變化幅度及其分布規律。周少祥等[6]針對火電機組構建了系統總熵產計算模型,并導出了超超臨界機組鍋爐煙氣余熱回收用于加熱凝結水的節約能量計算公式。Usn等[7]研究了熱力系統中效率較低部分的位置和量級,建立了系統中某一設備的損失和效率的分析計算模型。慈文斌等[8]提出一種多時間尺度電熱綜合能源系統狀態估計方法。劉剛[9]以鍋爐及其輔助系統為對象,研究了影響能效指標的底層因素,建立了基于神經網絡軟測量模型和主元分析的診斷模型。張春發等[10]綜合考慮煤質揮發分、灰分、水分變化及運行工況變化對鍋爐效率的影響,導出了鍋爐機械不完全燃燒損失q4的解析評估模型。孫浩祖等[11]研究了機組變工況運行時管道熱效率對機組運行能效的影響。劉磊[12]針對管道效率計算過程中存在的問題,改進了反平衡管道效率的計算方法,明確了管道效率對綜合系統節能潛力的影響規律。
上述研究均表明,子系統效率的改善且單獨作用于綜合系統均有利于綜合系統熱經濟性的提高。但是,實際系統運行過程中,由于子系統及其熱力設備對綜合系統運行性能產生的影響屬于多效率擾動源同時作用,實際運行值與僅考慮單效率擾動影響的計算值存在一定的偏差,綜合系統的運行性能并非最優。
為此,在總結單效率擾動模式下電廠熱力系統節能分析計算方法的基礎上,系統研究多效率擾動模式對綜合系統運行性能的影響機制,提出多個子系統或熱力設備的熱效率同時變化時綜合系統運行熱經濟性的能效分析與評價方法,以期為復雜熱力系統節能分析與能效評價提供理論支撐,為綜合系統的節能增效工作提供指導。
1 能效評價指標及其計算方法
圖1為典型火電廠原則性熱力系統,該系統是由鍋爐熱力系統、汽輪機熱力系統、管道系統、聯軸器及發電機電氣系統組成的一個復雜發電系統。

D1—全廠汽水損失; Dma—鍋爐補水量; HP—高壓缸; IP—中壓缸; LP1—低壓缸1; LP2—低壓缸2; TD—小汽輪機; FP—給水泵;HD—除氧器; SG—軸封加熱器; DE—凝結水精處理器; CP—凝結水泵; H1~H3, H5~H8均為回熱加熱器。
1.1 能效評價指標
火電廠運行能效評價指標中,供電標準煤耗率是發電廠各方面工作水平的反映,是火力發電系統運行熱經濟性能評價的總指標。與供電標準煤耗率緊密關聯的二級評價指標主要有發電標準煤耗率、全廠熱效率和熱耗率。其計算表達式分別為:
(1)
(2)
(3)
(4)
式中:bcp,n為供電標準煤耗率,kg/(kW·h);ξap為廠用電率,%;bcp,s為發電標準煤耗率,kg/(kW·h);ηcp、ηb、ηp、ηi、ηm、ηg分別為全廠熱效率、鍋爐熱效率、管道熱效率、汽輪機循環熱效率、機械效率和發電機效率,%;qcp為熱耗率,kJ/(kW·h)。
由式(2)~式(4)可知,qcp、bcp,s、ηcp三者知其一,即可求得其余2項,進而可求得其他能效評價指標。在工程應用中,一般情況下計算全廠熱效率較為方便。
1.2 能效評價指標的變化及其關系
進行電廠運行能效分析時,一般用能效指標的絕對變化量或相對變化率來表征其變化程度,表1給出了全廠熱效率、熱耗率和發電標準煤耗率變化值的計算公式[13],其中帶“ ′”者表示變化后的參數。

表1 能效指標的變化Tab.1 Changes in energy efficiency indicators
當采用發電標準煤耗率和熱耗率指標的相對變化率來表征電廠運行能效變化時,其相對變化率的絕對值是相同的[14],即
(5)
式中:δqcp和δbcp,s分別為qcp和bcp,s以變化前為基準的相對變化率。
工程應用中,全廠熱效率相對變化率的計算較為方便,故系統運行能效分析計算的主要任務就是導出全廠熱效率相對變化率δηcp的分析計算模型。據此,可求出電廠其他能效評價指標絕對變化量的計算公式。
發電標準煤耗率絕對變化量Δbcp,s:
(6)
年耗發電標準煤絕對變化量ΔBcp,s:
(7)
式中:Bcp,s為年耗發電標準煤,kg。
熱耗率絕對變化量Δqcp:
(8)
2 單效率擾動下全廠熱效率相對變化率的計算方法
發電系統運行過程中,當構成它的任意一個子系統或熱力設備的分熱效率單獨變動時,考慮到全廠熱效率的提高意味著能耗率降低這一普遍規律,熱耗率、發電標準煤耗率、全廠熱效率的相對變化率與各子系統熱效率相對變化率之間的普適關系式[14]可以寫為:
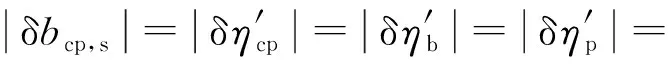
(9)
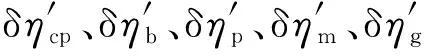
式(9)表明,當任意一個分熱效率單獨發生變動時,它們的相對變化率的絕對值是相同的,但絕對變化量不同。此時,可以通過計算汽輪機循環熱效率的相對變化率,再按照式(6)~式(8)來計算其他能效指標的絕對變化量,汽輪機循環熱效率相對變化率的計算可依據參考文獻[3]和文獻[4]進行,在此不詳細展開。
目前,多數電廠的節能工作都是根據式(6)~式(9)進一步求出全廠熱效率、熱耗率和發電標準煤耗率的相對和絕對變化量,以指導全廠節能減排工作。然而,在實際運行中,促使機組偏離基準工況運行的效率擾動源可能是單一的,也可能是多種擾動源同時存在且相互耦合作用的; 同時,單一擾動可能引起單個熱力設備效率發生變化,也可能引起多個熱力設備效率同時發生變化。因此,依據子系統或熱力設備的分效率單獨變化而得出的結果并不能全面反映發電系統運行能效的實際情況,綜合系統的運行性能不一定是最優的。因此,建立多效率擾動下發電系統運行能效的分析計算模型是電廠實現深度節能增效亟待解決的一個關鍵問題。
3 多效率擾動下全廠熱效率相對變化率的計算方法
多效率擾動條件下,計算綜合系統能效指標的首要工作是求得全廠熱效率的相對變化率。為使導出結果具有普適性,對于圖1所示的電廠原則性熱力系統,設某一運行工況下影響機組熱經濟性的各個參數或因素分別為x1、x2、x3、x4、…、xb、xp、xi、xm、xg(包括非運行和運行因素,非運行因素主要有煤質、送風溫度和循環水溫度等,運行因素主要有氧量、主蒸汽壓力和溫度、再熱蒸汽壓力和溫度等)。假定各參數間相互獨立、線性無關,且函數連續可導,微分計算過程中忽略高階無窮小量。則鍋爐熱效率ηb、管道熱效率ηp、汽輪機循環熱效率ηi、機械效率ηm、發電機效率ηg和全廠熱效率ηcp可表示為如下多元函數:
ηb=fb(x1,x2,x3,…,xb)
(10)
ηp=fp(x2,x3,x4,…,xp)
(11)
ηi=fi(x3,x4,x5,…,xi)
(12)
ηm=fm(x4,x5,x6,…,xm)
(13)
ηg=fg(x5,x6,x7,…,xg)
(14)
ηcp=ηbηpηiηmηg=fb(x1,x2,x3,…,xb)×
fp(x2,x3,x4,…,xp)×fi(x3,x4,x5,…,xi)×
fm(x4,x5,x6,…,xm)×fg(x5,x6,x7,…,xg)
(15)
3.1 2個分效率同時發生變化
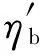
(16)
(17)
則全廠熱效率為:

(18)
其中,
Fimg(x)=fi(x3,x4,x5,…,xi)×fm(x4,x5,x6,…,xm)×fg(x5,x6,x7,…,xg)
(19)
全廠熱效率、鍋爐熱效率以及管道熱效率的絕對變化量分別為:
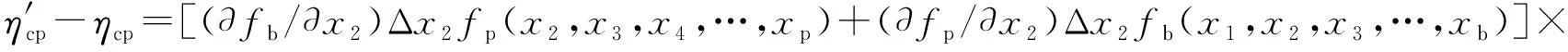
Fimg(x)
(20)
(21)
(22)
由此可得鍋爐熱效率和管道熱效率的相對變化率之和為:
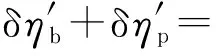
(23)
全廠熱效率的相對變化率為:
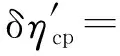
(24)
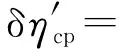
(25)
由式(25)可知,當參數x2變化引起鍋爐熱效率ηb和管道熱效率ηp變化而其他熱力設備的熱效率不發生改變時,全廠熱效率的相對變化率近似等于鍋爐熱效率和管道熱效率的相對變化率之和。
可以推理得出,在電廠實際運行過程中,當某些參數變化引起任意2個子系統或熱力設備的熱效率發生變化而其他子系統或熱力設備的熱效率不變時,全廠熱效率的相對變化率近似等于這2個子系統或熱力設備分效率的相對變化率之和。

(26)
它們的絕對變化量分別為:
(27)
它們的相對變化率分別為:
(28)
將式(27)和式(28)代入式(26),經數學推導,得:
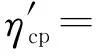
(29)
又因為
(30)
聯立式(29)和式(30),推導并整理可得:
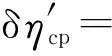
(31)
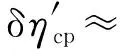
(32)
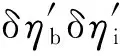
(33)
由式(33)可得出如下結論:當ηp、ηm和ηg為固定值時,鍋爐熱效率和汽輪機循環熱效率同時發生變化的情況下,全廠熱效率的相對變化率近似等于鍋爐熱效率相對變化率與汽輪機循環熱效率相對變化率之和。
3.2 3個分效率及以上同時發生變化
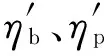
(34)
(35)
(36)

(37)
式(37)中:
Fmg(x)=fm(x4,x5,x6,…,xm)×fg(x5,x6,
x7,…,xg)
(38)
全廠熱效率、鍋爐熱效率、管道熱效率和汽輪機循環熱效率的絕對變化量分別為:
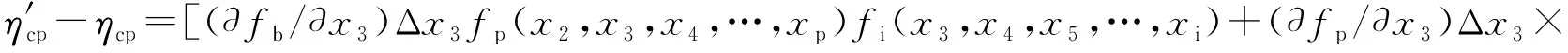
fb(x1,x2,x3,…,xb)fi(x3,x4,x5,…,xi)+
(?fi/?x3)Δx3fb(x1,x2,x3,…,xb)×
fp(x2,x3,x4,…,xp)]Fmg(x)
(39)
(40)
(41)
(42)
由此可得鍋爐熱效率、管道熱效率和汽輪機循環熱效率的相對變化率之和為:
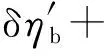
(43)
則全廠熱效率的相對變化率為:
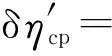
(44)
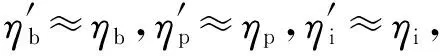

(45)
由式(45)可知,當參數x3變化引起ηb、ηp和ηi變化,而其他熱效率不發生改變時,全廠熱效率的相對變化率近似等于ηb、ηp和ηi的相對變化率之和。
同理,電廠實際運行過程中,當某些參數變化引起任意3個子系統或熱力設備的熱效率同時變化而其他子系統或熱力設備的熱效率不變時,全廠熱效率的相對變化率近似等于這3個子系統或熱力設備分效率的相對變化率之和。
當機組運行過程中因運行參數變化引起ηb、ηp、ηi、ηm和ηg中的4個或5個分效率同時變化時,采用同樣的方法,可以推得如下關系式:
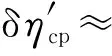
(46)
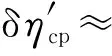
(47)
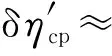
(48)
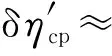
(49)
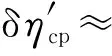
(50)
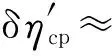
(51)
由式(46)~式(51)可得出如下結論:當因運行參數變化引起ηb、ηp、ηi、ηm和ηg中的4個或5個分效率同時發生變化時,全廠熱效率的相對變化率近似等于相應的4個或5個分效率的相對變化率之和。
需要說明的是,上述公式是以電廠原則性熱力系統為對象導出的,但其結果也適用于鋼鐵、冶金和石化等行業系統運行能效的分析和評價。當采用熱力學第二定律的方法來進行系統能效評價時,其結果也是適用的。因此,上述方法具有一定的普適性。
4 誤差分析
前述多效率擾動時電廠熱力系統能效分析計算模型是在忽略高階無窮小的情況下導出的,為此,需要對該模型進行誤差分析,以驗證本文所構建的計算模型能否滿足工程應用的需要。實際值采用變化后的各子系統分效率的連乘積進行計算,計算值采用本文構建的多效率擾動下復雜熱力系統能效分析與評價方法得出。
4.1 分效率同時變化時的誤差分析
分效率同時變化時,全廠熱效率實際值與計算值之間的誤差數據見表2~表5。由表2~表5可以看出,保持各子系統的分效率初始值不變,多個分效率同時變化時,全廠熱效率計算值與實際值誤差較小,近似一致。同時,分效率的變化幅度越大、變化個數越多,全廠熱效率計算值與實際值的偏差也越大。當5個分效率同時變化,且各個分效率變化幅度均為0.6%時,全廠熱效率計算值與實際值的偏差最大,但其絕對誤差僅為0.000 239,相對誤差為0.055 8%,完全滿足工程實際應用要求。

表2 2個分效率同時變化時的誤差計算數據1)Tab.2 Calculated error data for simultaneous changes in two sub-efficiencies

表3 3個分效率同時變化時的誤差計算數據1)Tab.3 Calculated error data for simultaneous changes in three sub-efficiencies

表4 4個分效率同時變化時的誤差計算數據1)Tab.4 Calculated error data for simultaneous changes in four sub-efficiencies

表5 5個分效率同時變化時的誤差計算數據1)Tab.5 Calculated error data for simultaneous changes in five sub-efficiencies
4.2 不同分效率初始值情況下,分效率同時變化0.2%時的誤差分析
在工程實際應用中,較少出現多個分效率同時變化較大的情況,而多個分效率基于初始值小范圍波動的情況較為常見。表6~表9給出了分效率同時變化2%時的誤差計算數據。由表6~表9可知,在各個分效率初始值不同的情況下,得到的全廠熱效率計算值與實際值誤差較小,近乎一致。分效率變化的個數越多、初始值越大,全廠熱效率計算值與實際值的偏差也越大。當各個分效率初始值分別為ηb=95%、ηp=98.5%、ηi=47.5%、ηm=99.5%、ηg=99.5%,各分效率同時變化0.2%時,全廠熱效率計算值與實際值的偏差最大,其絕對誤差為0.000 026 5,相對誤差為0.005 96%,滿足工程實際應用要求。

表6 2個分效率同時變化0.2%時的誤差計算數據1)Tab.6 Calculated error data for a simultaneous 0.2% variation in two sub-efficiencies

表7 3個分效率同時變化0.2%時的誤差計算數據1)Tab.7 Calculated error data for a simultaneous 0.2% variation in three sub-efficiencies

表8 4個分效率同時變化0.2%時的誤差計算數據1)Tab.8 Calculated error data for a simultaneous 0.2% variation in four sub-efficiencies

表9 5個分效率同時變化0.2%時的誤差計算數據Tab.9 Calculated error data for a simultaneous 0.2% variation in five sub-efficiencies
從誤差分析結果可以看出,分效率同時變化的個數越多,對全廠熱效率的影響權重就越大。因此,僅考慮單個熱效率擾動來進行綜合系統能效分析與評價是不科學的,只有在多效率擾動條件下進行綜合系統能效分析與評價,才能科學評價綜合系統的運行能效,進而促進綜合系統的節能增效。
5 結 論
(1) 對于單熱效率擾動,全廠熱效率的相對變化率等于各子系統或熱力設備分效率的相對變化率。
(2) 經過嚴謹的數學推演,導出了多效率擾動條件下全廠熱效率的相對變化率等于相關子系統或熱力設備分效率的相對變化率之和;通過誤差分析,驗證了據此進行電廠運行能效的分析與評價更符合現場實際情況。該方法可以定量計算出多個子系統或熱力設備的分效率同時變化時對全廠熱效率的影響規律及其權重大小,進而可計算出電廠熱耗率、煤耗率等能效評價指標的大小及其分布規律,為協調優化各熱力設備提供了理論支撐。
(3) 根據誤差分析結果,分效率同時變化的個數越多,對全廠熱效率的影響權重就越大。因此,只考慮單效率擾動來進行綜合系統的能效分析與評價難以促進復雜熱力系統深度節能。本文所建立的多效率擾動下電廠熱力系統能效分析與評價模型也適用于其他行業由多個子系統構成的復雜熱力系統。若采用熱力學第二定律來分析,按照同樣的處理手段,也可以得出類似的計算模型。

