基于GASA-BP神經網絡的煤層瓦斯含量預測方法研究*

馬 磊，陸衛東，魏國營,,3

(1.河南理工大學 安全科學與工程學院，河南 焦作 454000；2.新疆工程學院 安全科學與工程學院，新疆 烏魯木齊830023；3.煤炭安全生產與清潔高效利用省部共建協同創新中心，河南 焦作 454000 )

0 引言

煤層瓦斯含量是描述單位質量煤容納瓦斯體積的量，是預測瓦斯涌出量和煤層突出危險性的重要參數，瓦斯含量的精準預測對瓦斯災害治理具有重要意義[1-2]。

近年來，隨著機器學習和智能算法的快速發展，人工神經網絡、支持向量機和極限學習機等方法在煤層瓦斯預測中得到了廣泛應用[3-5]。魏國營等[6]利用主成分分析法(Principle Component Analysis,PCA)提取瓦斯含量影響因素的主成分，并用自適應混合粒子群算法優化支持向量回歸機(Vector Regression Machine,SVM)的初始參數構建PCA-AHPSO-SVR瓦斯含量預測模型；林海飛等[7]利用粒子群優化算法(Particle Swarm Optimization,PSO)優化BP神經網絡(Back Propagation Neural Network,BPNN)的初始權值和閾值，構建PSO-BPNN瓦斯含量預測模型；汪吉林等[8]將構造指數、煤層埋深、煤層厚度和原始瓦斯含量作為模型輸入，構建BPNN瓦斯含量損失量預測模型；曹博等[9]采用PCA法降低數據維度，利用遺傳算法(Genetic Algorithm,GA)搜索BPNN的初始參數，構建GA-BPNN瓦斯含量預測模型；溫廷新等[10]利用改進的果蠅優化算法優選極限學習機(Extreme Learning Machine，ELM)的參數建立IFOA-ELM瓦斯預測模型；付華等[11]利用蟻群聚類(Ant Colony Clustering，ACC)算法優化Elman神經網絡建立絕對瓦斯涌出量預測模型。對BPNN易陷入局部極小的陷阱且收斂速度慢的問題，學者都利用改進了的單一算法優化模型初始參數，但瓦斯含量影響因素多且各影響因素之間非線性關系復雜，再加上單一智能算法的改進程度的局限性導致預測模型穩定性和準確率低。為解決這類問題，將GA和具有時變且最終趨于零概率突跳性的模擬退火(Simulated Annealing，SA)算法整合成GASA混合優化算法，該算法吸取2類算法的優點，克服GA易早熟的缺點，提升BPNN的尋優訓練速度和最優解質量。

本文擬利用灰色關聯分析法篩選瓦斯含量的地質影響因素，建立預測參數體系，將GA和SA整合為GASA混合算法協同初始化BPNN參數建立GASA-BPNN瓦斯含量預測模型，以期得到更高效和精準的預測模型。

1 建立模型

1.1 相關理論

GA是模擬自然界遺傳機制和達爾文生物進化論的并行隨機搜索算法[12]。GA將待優化的參數編碼為若干個個體形成群體，通過遺傳操作來效仿生物的進化過程，利用適應度值來評價個體的質量，通過循環迭代和適應度函數引導種群共同進化，使最優個體逼近問題全局最優解。

SA[13]是基于Monte Carlo迭代求解策略的1種隨機搜索算法，出發點是基于固體物質的退火過程與組合優化問題之間的相似性。SA由初始高溫開始，利用具有概率突跳性的Metropolis抽樣準則以一定概率接受鄰域中次優解隨機搜索，隨著溫度不斷下降，最終找到全局最優解。

依據SA在搜索過程中逐漸趨于0的概率突跳性和GA優勝劣汰的優勢，將GA和SA整合成GASA混合算法，避免算法落入局部極小的陷阱；在結構方面，GA是依據鄰域函數對群體并行搜索，而SA每次搜索時只針對1個個體，GASA混合算法相當于在GA中群體的每個個體下均串行1個SA，使個體的鄰域搜索結構更加豐富，增強算法搜索能力和效率。GASA算法優化流程包括以下10個步驟[14]：

1)初始化GA。設定種群規模N，初始化種群PK，設定最大遺傳代數M，遺傳迭代次數K=1。

2)定義適應度函數。

3)評價PK適應度值。判斷是否滿足遺傳停機條件？若滿足，選擇適應度最大的個體作為最優解輸出，算法結束；若不滿足，執行步驟4)～9)。

4)對種群PK執行遺傳交叉和變異生成種群PK0，并評價PK0適應度值。

5)初始化SA參數。設定種群PK0為SA的初始解，令i=0，設定初溫T=Ti(足夠高)，確定每個T狀態下Metropolis鏈長L，令鏈中迭代次數Q=1。

6)對當前溫度T和Q=1,2,3,…L狀態下，重復執行步驟7)～9)。

7)對當前群體的每個個體隨機擾動產生新的群體，評價新群體適應度。

8)計算新群體和當前群體各個體適應度值的差值ΔE。若-ΔE<0，則接受新個體；若-ΔE≥0，計算接受概率，即判斷P=exp(-ΔE/T)≥rand是否成立，若成立，也接受新解；否則拒絕新解。

9)令Q=Q+1，判斷條件Q>L是否成立，若成立，則i=i+1，按溫度衰減函數進行降溫，即T=Ti+1，其中TL不成立，則轉至步驟7)。SA停機條件通常為設置停機溫度。

10)PK種群經遺傳操作產生種群PK0，種群PK0作為SA的初始解經退火操作產生PK+1，若新種群PK+1沒有滿足遺傳停機條件，則由SA產生的種群PK+1作為GA的初始種群再參加迭代尋優。

1.2 建立GASA-BPNN預測模型

BPNN是由誤差逆向傳播算法訓練的多層前饋神經網絡，在結構上由輸入層、若干隱含層和輸出層組成，各層采用權重參數全連接方式，其核心是信息從輸入層經隱含層處理后傳遞到輸出層計算誤差，若誤差不滿足要求，將誤差信號反向傳遞給各節點，節點更新參數，反復迭代直至滿足要求，最終構建能逼近復雜非線性映射的模型[15]。但BPNN初始參數對模型性能的影響十分敏感，隨機初始化參數是導致BPNN陷入局部極值、收斂速度慢和模型精度低的主要原因。因此，利用GASA算法初始化BPNN的參數來代替傳統方法，有效地提高BPNN訓練速度和預測精度，GASA算法初始化BPNN參數具體流程如圖1所示。

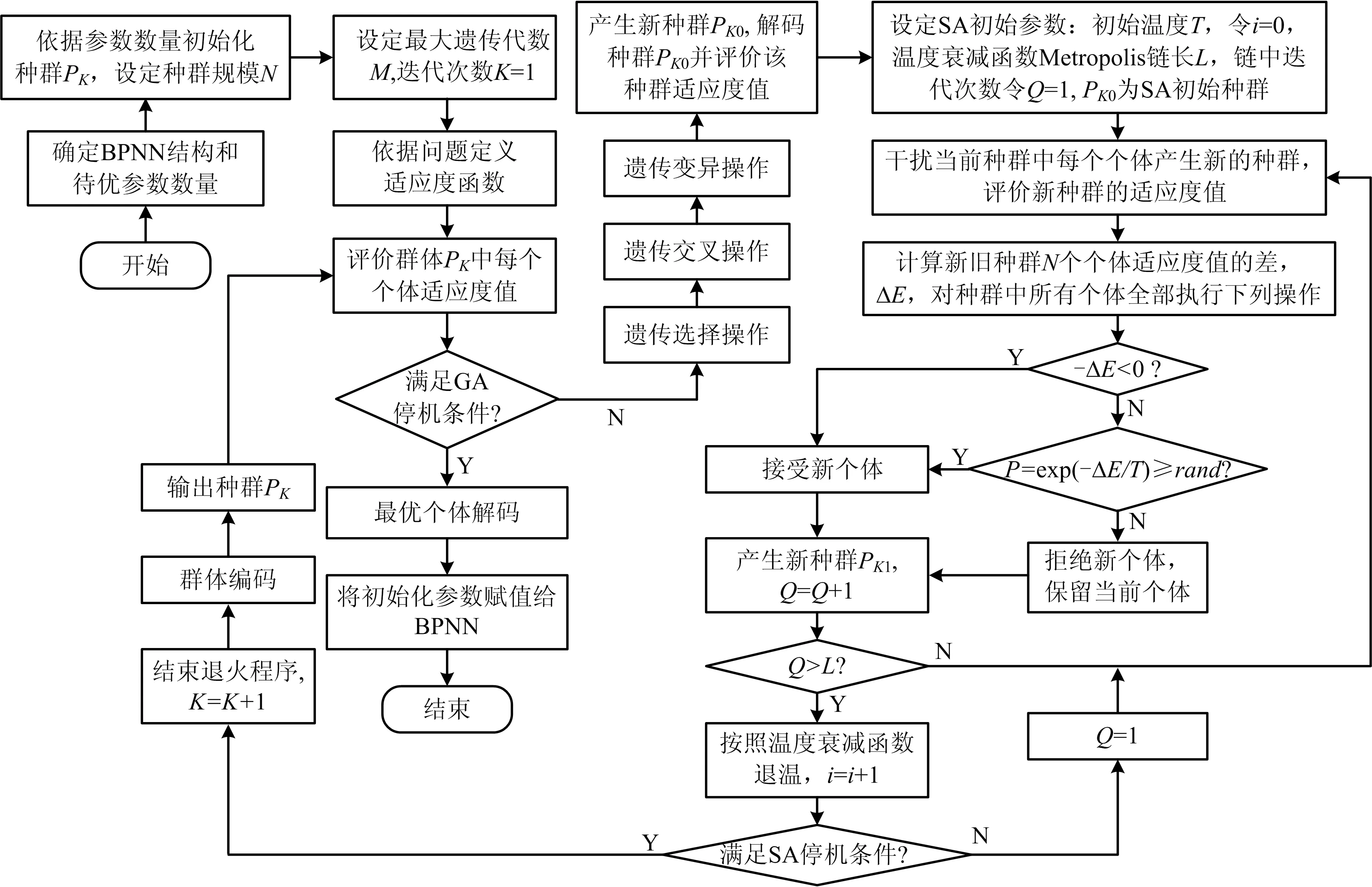
圖1 GASA初始化BPNN參數流程Fig.1 Procedure of GASA to initialize BPNN parameters

2 現場應用

2.1 瓦斯含量影響因素分析及建立數據集

根據焦作礦區某礦瓦斯地質條件和瓦斯分布規律研究情況[16]，瓦斯含量(X0,m3/t)影響因素選取可量化處理的以下8個因素：煤層埋深(X1,m)、煤層厚度(X2,m)、傾角系數(X3)、上覆基巖厚度(X4,m)、圍巖等效系數(X5)、斷層復雜系數(X6)、褶皺復雜系數(X7)和底板標高(X8,m)[6]。在該礦選取300組瓦斯含量及影響因素的數據作為實驗數據集，訓練集和測試集利用10折交叉驗證的方式劃分，部分數據見表1。

表1 瓦斯含量及影響因素數據Table 1 Data of gas contents and influencing factors

2.2 確定BPNN結構

利用灰色關聯分析法篩選主控因素為模型的輸入。灰色關聯計算步驟如下[17]：

1)確定參考序列和比較序列：參考序列為瓦斯含量(X0)，比較序列為瓦斯含量的8個影響因素。

2)數據按公式(1)進行歸一化處理。

(1)

式中：xl(h)為樣本編號為h的第l評價指標的數值；h為樣本編號，h=1,2,…,n；l為評價指標，即瓦斯含量的各影響因素，l=1,2,…,m；xmax和xmin分別是評價指標的最大和最小值。

3)按公式(2)計算關聯度系數。

(2)

式中：ξe(k)為比較序列xe對參考序列x0在第k指標上的關聯系數，k=1,2,…,n；ρ∈[0,1]為分辨系數。

4)按公式(3)計算關聯度。

(3)

式中：n為樣本數量；wk為指標權重。

關聯度計算結果見表2。由表2可知：影響因素X4和X5的關聯度相近，說明這2個因素對含量影響效果一樣，只需保留1個即可說明效果，因此，剔除X5。因素X3和X7的關聯度不足0.5，屬低相關度，因此剔除，從而確定輸入層節點數為5。

表2 灰色關聯分析結果Table 2 Results of grey correlation analysis

BPNN隱含層節點數過少會造成參數無法得到充分訓練和預測精度低的問題，節點過多會造成過擬合現象。依據經驗公式(4)確定隱含層節點數范圍為[4,12][18]：

(4)

式中：W為隱含層節點數；c是輸入層節點數；q為輸出層節點數；B是1～10范圍內的整數。

通過比較不同節點數模型的誤差試湊出最佳隱含層節點數，結果見表3。由表3可知：當W=12時誤差最小，因此，網絡隱含層節點確定為12。研究表明三層BPNN能任意逼近任何復雜非線性系統，因此，GASA-BPNN預測模型的結構被確定為5-12-1型BPNN。

表3 隱含層節點數與平均相對誤差Table 3 Numbers of hidden layer nodes and average relative errors

2.3 模型應用

模型應用具體流程如下[14]：

1)劃分測試集與訓練集。首先將數據按公式(1)歸一化到[0,1]范圍內。然后將數據集分層抽樣劃分10個互斥子集，每次利用某個子集作為測試集，其余作為訓練集進行10組訓練和測試，重復10次，10折交叉驗證示意如圖2所示[19]。

圖2 10折交叉驗證示意Fig.2 10-fold cross-validation diagram

2)GA種群初始化。采用浮點數的編碼規則對85個參數進行編碼，每個個體代表1套權值和閾值，并隨機生成50個個體的種群PK。

3)GA參數設定。設定遺傳最大迭代次數為300，迭代次數K=1，當滿足最大遺傳迭代次數時遺傳停機，交叉概率pc=0.7，變異概率pm=0.005。

4)定義適應度函數。適應度函數根據預測均方誤差(Mean Square Error，MSE)進行設定，MSE越小，個體適應度值越大。

5)評價初始種群PK每個個體的適應度，依據適應度值進行排序。

6)GASA停機判定。判斷是否滿足最大遺傳迭代次數，若滿足，則優化結束，轉至步驟7)～11)；否則，K=K+1，轉步驟12)。

7)初始化BPNN。將步驟6)優化后的解賦值給BPNN，設定最大訓練次數為H=750，記錄迭代次數為S=0，隱含層和輸出層的激活函數分別選擇logsig函數和purelin函數。

8)輸入數據集。數據按照BPNN的正向向前傳輸，第f個隱含層神經元的輸入如式(5)所示：

(5)

式中：γf為第f個隱含層神經元的輸入；vvf是輸入層第v個神經元和隱含層第f個神經元之間連接的權值。

第j個輸出節點的輸入如式(6)所示：

(6)

式中：βj為第j個輸出神經元的輸入；wfj為隱含層第f個神經元與輸出層第j個神經元的連接權值；bf為隱含層第f個神經元的輸出。

9)更新BPNN權值和閾值。預測均方誤差反向傳播給各個節點，節點誤差自適應學習率梯度下降法更新參數如式(7)所示：

(7)

式中：μ(S+1)為第S+1代的學習率；μ(S)為第S代的學習率；Sin為增量系數；Sde為減量系數；E(S+1)為第S+1代的誤差；E(S)為第S代的誤差。

當誤差以較少的趨勢逼近目標值時，表明模型訓練方向正確，可增大學習速度；當誤差的增加超過允許范圍時，表明模型訓練方向錯誤，應降低學習率。

10)BPNN停機判定。判斷是否滿足停機條件(設定最小誤差為停機條件)，若滿足，網絡結束學習完成模型建立，轉步驟11)；否則判斷是否H=S，若是則返回7)；若不是，則S=S+1返步驟8)。

11)模型仿真及評價。將測試集輸入GASA-BPNN模型測試，利用MSE、迭代次數和預測相對誤差進行模型性能評價。

12)GA選擇。采用輪盤賭選擇法篩選個體，個體xu的適應度值為f(xu)，則個體xu被選擇的概率為式(8)：

(8)

式中：N為群體中個體數目總和。

(9)

式中：λ1+λ2=1，λ1>0，λ2>0。

14)GA變異。隨機選擇個體基因型X=x1x2…xb…xS，將xb作為突變點，按公式(10)進行遺傳運算。

(10)

式中：UB,LB分別為xb的上、下邊界值；r為隨機數；K為進化代數；Δ(t,y)的定義為式(11)：

(11)

式中：q為控制非一致性參數，取0.8。

15)評價PK0適應度。評價PK0的適應度值，設定PK0為退火算法的初始種群。

16)SA參數初始化。將所有經過遺傳運算的個體進行退火。設定初始溫度T=100 ℃，冷卻系數0.98，停機準則，令Q=1，馬爾可夫鏈長L=60。

17)對群體中的每個個體進行擾動產生1個新解，計算新舊群體每個個體的適度值的差值，根據Metropolis抽樣準則判斷是否接受新解。

18)令Q=Q+1，判斷是否在馬爾可夫鏈中，若在則轉步驟17)，若不在鏈中，則退溫，再判斷是否達到SA停機條件，如滿足停機，則SA算法結束，轉步驟4)；否則，Q=1，轉步驟17)。

2.4 模型性能對比與結果分析

為了驗證GASA-BPNN瓦斯含量的預測效果，在同等條件下分別建立BPNN和GA-BPNN模型對比分析。首先利用GA算法和GASA算法分別初始化BPNN的參數30次，最優個體的平均適應度變化曲線如圖3所示，由圖3可得GASA算法和GA優化過程平均適應度分別在第92次和第177次迭代時完成尋優，GASA算法尋優速度明顯快于GA算法并且最優適應度大于GA算法的最優適應度，說明GASA算法在參數尋優過程中效率和效果均優于GA算法。

圖3 平均最優個體適應度值曲線Fig.3 Curves of average optimal individual fitness value

其次，將經過10次10折交叉驗證劃分的100組訓練集分別輸入BPNN模型、GA-BPNN模型和GASA-BPNN模型中按照誤差自適應學習率梯度下降法進行參數學習，3種模型分別訓練100次，100次訓練平均均方誤差曲線如圖4所示，圖4顯示GASA-BPNN和GA-BPNN分別在第332次和第459次訓練時達到目標誤差線，而BPNN在第736次訓練時仍未達到目標誤差，說明經GASA優化后的模型對樣本學習所需的訓練次數明顯減少并且權值和閾值更接近最優參數。

圖4 平均均方誤差收斂曲線Fig.4 Curves of average mean square error convergence

最后，將100個測試樣本集分別輸入3種模型中預測計算，各組預測平均相對誤差見表4，從表4可知，各組GASA-BPNN模型預測的平均相對誤差和10組總平均相對誤差明顯低于其他模型。

表4 各組測試集平均相對誤差Table 4 Average relative error of each group of test set %

選取樣本編號為1到30的30個樣本集作為研究對象，分析30個樣本在10組仿真測試中均是測試集時的預測性能，得到實測值與平均預測值對比如圖5所示，平均預測相對誤差對比如圖6所示。由圖5可得GASA-BPNN的預測值較GA-BPNN和BPNN最接近實測值，由圖6可得GASA-BPNN模型預測的平均相對誤差最小且相對誤差波動最小，說明GASA-BPNN模型預測穩定性強并且預測準確率更高，能滿足預測目標和工程需求。

圖5 實測值與平均預測值對比Fig.5 Comparison of measured values and average predicted values

圖6 平均預測相對誤差對比Fig.6 Comparison of average prediction relative error

3 結論

1)將GA和具有時變概率突跳性的SA整合為GASA算法，該策略突破了單一智能算法改進程度的局限性，相同環境下該算法在BPNN初始參數尋優過程中效率和效果均優于GA算法。

2)利用灰色關聯分析法消除瓦斯含量影響因素相關性，建立瓦斯含量預測參數體系從而確定BPNN輸入層節點個數，減少數據維度，降低模型訓練的計算量和預測誤差。

3)利用GASA算法優化BPNN的權值和閾值，有效地解決BPNN收斂速度慢和易陷入極小的問題，與其他模型相比，經過GASA優化的BPNN對數據的學習迭代次數明顯減少并且GASA-BPNN模型能更加準確地預測瓦斯含量，對煤礦瓦斯治理具有重要意義。