基于GA-BP神經網絡的深基坑變形最優化預測研究
邱章龍
(中鐵七局集團武漢工程有限公司,湖北 武漢 430000)
1 概述
隨著我國經濟發展水平不斷提高,基礎設施建設更新需求日益增加,高速公路作為我國公共交通基礎設施的重要一環,國民經濟發展上發揮著至關重要的作用。由于城市地上空間的制約,地下空間的拓展利用逐漸增多,城區復雜環境下明挖隧道施工技術趨于成熟,與此同時深基坑施工技術也得到愈加廣泛的應用,傳統基坑監測方法忽視地下水位的預警,錯失解決問題的良機,因此造成重大安全問題。地下水位隨時間呈不規則非線性變化,具有優越的非線性動態處理能力的BP神經網絡被廣泛用于預測。目前,不少研究人員依托實際工程構建了多種BP神經網絡模型用于工程預測。季慧等[1]運用了一個基于混沌的局部搜索技術大大提高了算法收斂速度;劉海龍等[2]利用遺傳算法對BP神經網絡進行改進操作,提高了模型的穩定性和預測能力;黃震等[3]構建了基于模擬退火法的SA-BP神經網絡預測模型對軟土基坑開挖墻后最大地表沉降進行預測,并進行了對比和驗證;謝饒青等[4]提出一種基于NPCA-GA-BP神經網絡預測方法提高了采場穩定性;劉蕊蕊等[5]通過遺傳算法和拉文伯格-馬爾夸特算法改善了BP算法收斂速度慢,易收斂到局部極小點的問題。
為了提高工程進展的高效性和穩定性,本文依托廣州新白云國際機場第二高速公路南段工程新塘互通立交路段大觀路隧道工程,就城區復雜環境下明挖隧道深基坑開挖過程中土體及地下水位監測數據展開預測優化研究。通過實時監測數據進行分析,結合城市軌道交通工程監測技術規范,提出工程優化策略,實現科學、優質、安全、高效的現代項目管理。
2 工程概況
2.1 工程基本情況
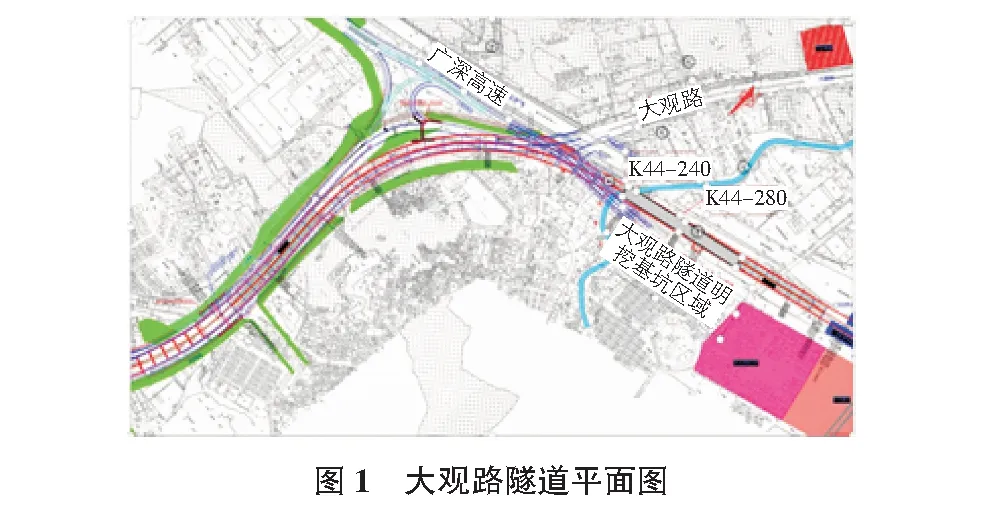
工程主體為總長度1 520 m的明挖隧道,隧道于天河區大觀中路新園新村附近起始,終點位于廣深高速公路廣氮收費站,里程范圍從K44-240到K44-280,其中地下暗埋長度945 m,地面敞開長度575 m。大觀路隧道平面圖如圖1所示。
2.2 地質條件
施工現場鉆探結果顯示:地質從上到下依次為全新統人工填土層、全新統河流相沖積層、上更新統河流相沖積層及殘積層。
其中,全新統人工填土層包含部分地段呈層狀分布的褐灰色雜填土以及大部分地段呈層狀分布黏性土;全新統河流相沖積層主要包含場區部分地段的呈似層狀分布的粉質黏土,絕大部分地段的呈層狀連續分布的粉質黏土;沖積層揭露于場區大部分地段的呈層狀粉質黏土和場區部分地段的呈似層狀分布的粉質黏土;殘積層裸露于場區部分地段的呈透鏡狀分布的可塑狀砂質黏性土以及呈層狀分布的砂質黏性土。
2.3 氣候條件
施工現場所屬地區為亞熱帶季風氣候,全年降雨量十分充沛,夏季炎熱,冬季溫暖。第二、三季度受洋流影響,以偏南風、天氣炎熱、降雨量大為主要特征。
2.4 監測方案
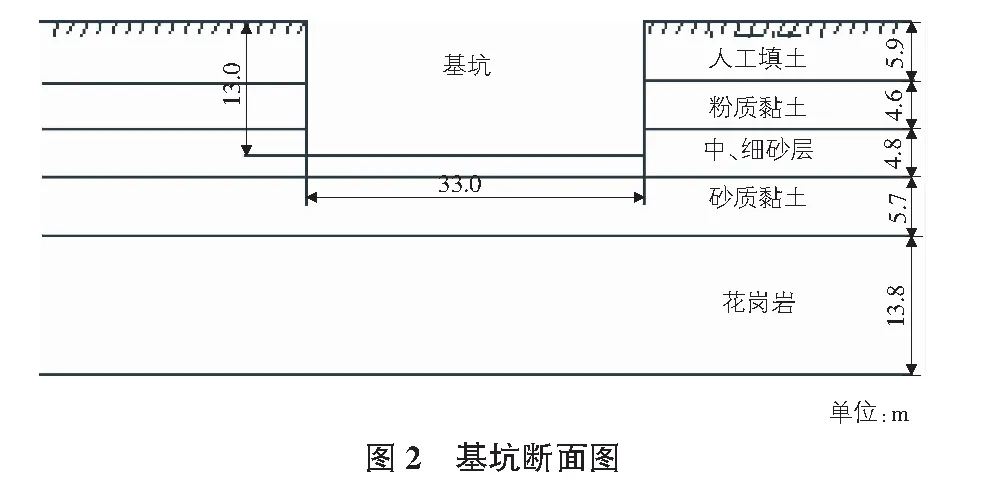
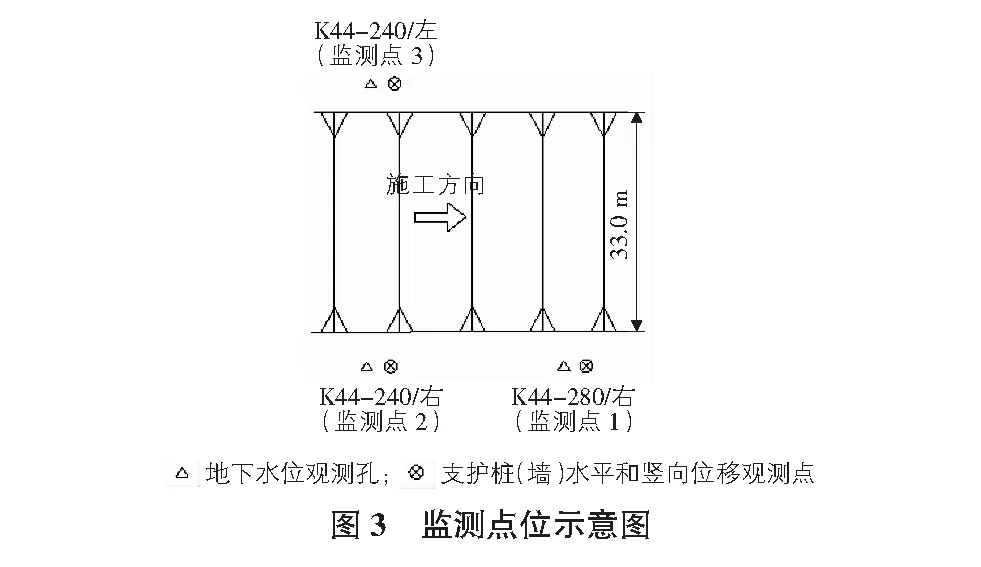
施工工程中實際位移越大,風險系數越高,因此將位移較大點位設為風險點位進行監測,同一點位布置1個~3個監測點,同時進行地下水位監測、樁頂沉降及水平位移監測,監測點位置距離基坑側面6 m,基坑斷面圖如圖2所示。其中樁(墻)頂沉降監測、樁(墻)頂水平位移監測、地下水位各3個測點,監測點位示意圖如圖3所示。
2.5 現場實測
本文主要在已開挖的里程范圍段關鍵點位進行了樁頂沉降及水平位移、樁體深層水平位移、地下水位、立柱結構豎向位移的監測工作,本次監測時間從2021年9月1日持續至2022年2月23日,其中地下水位、樁(墻)頂豎向位移、水平位移初始數據由勘察報告得出。圖4,圖5為數據監測傳感器安裝現場。

2.6 現場監測數據分析
施工過程監測點數據保持穩定,附近支撐軸力測點最大累計變化值為1 469.30 kN,地下水位測點最大累計變化值為-0.80 m,地下水位測點最大累計變化值為-17.7 mm,樁體深層水平位移測點最大變化值為20.84 mm,支護樁(墻)頂部豎向位移測點最大變化值為-19.30 mm,支護頂部水平位移測點最大變化值為23.19 mm,立柱結構豎向位移最大變化值-13.70 mm,累計變化值均在控制值范圍內,風險可控。
從現場監測數據分析來看,每個監測點的數據都有相似的規律性,不同的因素對地下水位影響程度如圖6,圖7所示。隨著墻體水平位移增大,地下水位值也逐漸增大,變化曲線從陡峭向平緩過渡,隨著立柱結構豎向位移增大,地下水位值逐漸減小,曲線曲率變化小。
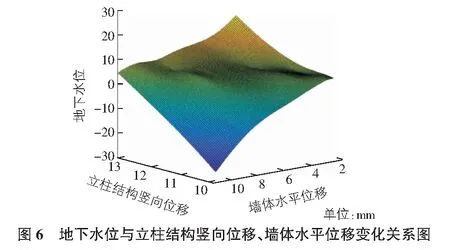
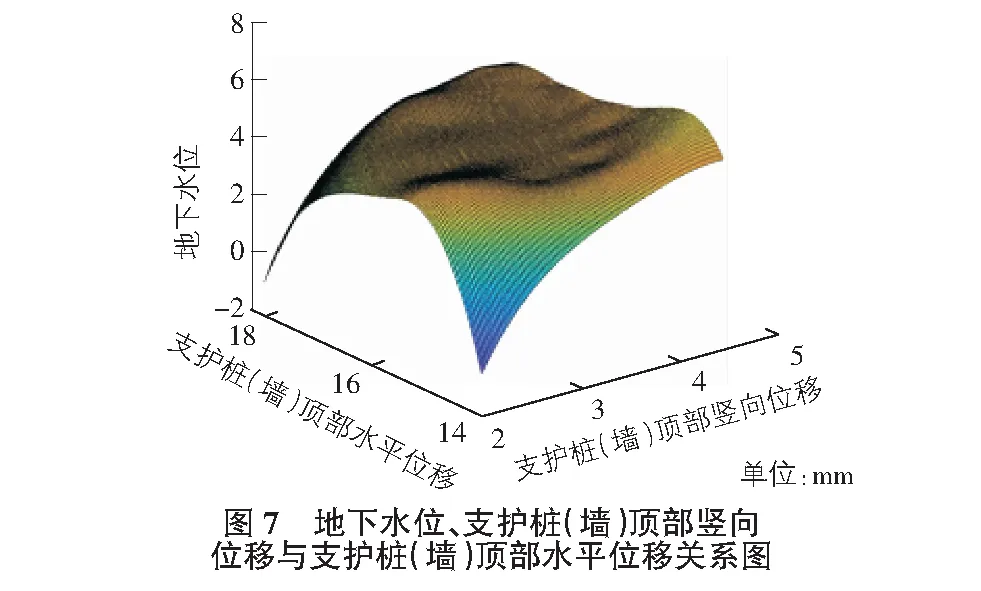
支護樁(墻)頂部豎向位移增大時,地下水位值呈現先減小后增大的變化趨勢,且減小段曲率較大增大段曲線較為平緩,支護樁(墻)頂部水平位移與地下水位值呈反比關系。
總體來看,地下水位與立柱結構豎向位移、墻體水平位移、支護樁(墻)頂部豎向位移、支護樁(墻)頂部水平位移表現出緊密的關聯性和規律性,而且呈現非線性變化。每一個變量都有合適值,偏離合適值有可能產生不良后果,例如地下水位過高,會引起淺基礎地基承載力的降低,巖土體在部分地區例如有的地震砂土地區易產生變形、崩塌等嚴重地質災害;地下水位過低,容易導致周邊道路、建筑物等沉降不均而傾斜、坍塌等等,因此,有必要對地下水位值進行優化預測[6]。
3 GA-BP神經網絡
BP神經網絡包括輸入層、隱含層、輸出層,BP神經網絡正向傳播過程中,輸入層輸入信號后,隱含層對信號逐層處理再從輸出層輸出,當結果與期望值存在較大偏差時,誤差信號沿原通道反向傳播,在不斷調整各層神經元的權閾值方法下,輸出誤差信號不斷減至最小,信號單向傳遞時下一層狀態只受上一層影響。所以BP神經網絡利用誤差反向傳播訓練前饋網絡,系統地解決了多層中隱含單元連接權的學習問題。本文選取該施工項目監測數據中與地下水位相關的立柱結構豎向位移、墻體水平位移、支護樁(墻)頂部豎向位移、支護樁(墻)頂部水平位移4個數據作為輸入量,地下水位值作為輸出量,單層隱含量節點為7,BP神經網絡結構如圖8所示。
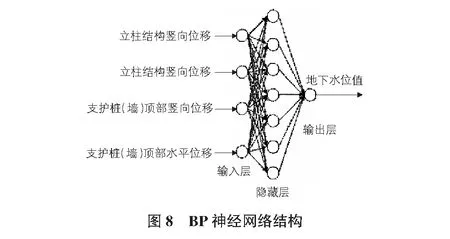
BP神經網絡簡單實用,執行效率高,具有強大的自適應能力,無論是在理論分析還是在實際的應用方面都比較成熟,但是依然存在網絡收斂速度慢和容易陷入局部極小值的不足[7]。因此,為了實現更好的預測效果需要引入遺傳算法(GA)進行改善[8],遺傳算法(GA)屬于一種生物智能算法,通過借鑒生物染色體交叉變異保留優良個體的特性,不斷篩選優化BP神經網絡的權值和閾值,極大地減小了輸出誤差,提高算法穩定性。BP神經網絡算法流程以及GA算法的優化過程如圖9所示。
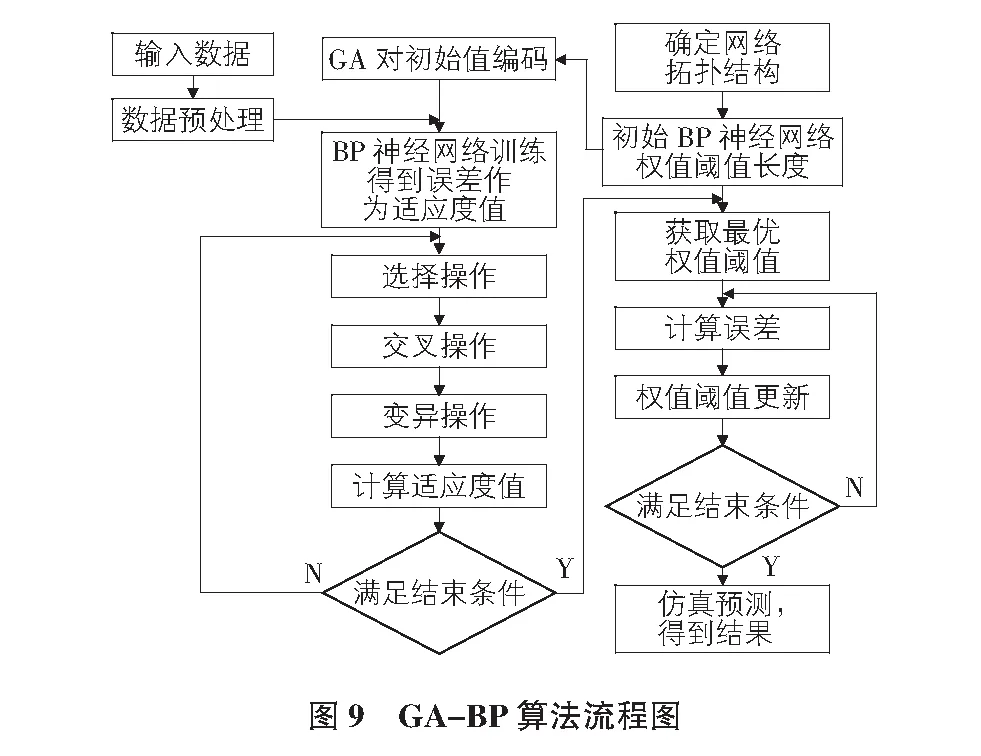
3.1 基于GA-BP神經網絡算法的預測優化算法應用
實驗步驟如下:
1)選取K44-280段監測點1右端的實測數據為樣本,將數據導入MATLAB并做歸一化處理,設置變量的取值范圍和染色體長度。
2)利用BP神經網絡的自適應性以及誤差負反向傳播特性,可采用遺傳算法優化BP神經網絡的權值和閾值,采用適應度為優化評價標準,適應度為BP神經網絡輸出值的絕對誤差累加響應,適應度值越低,代表網絡權值和閾值最優,收斂效果越好[9-11]。
3)在得到最優的權值和閾值后設定BP神經網絡參數,對樣本數據進行神經網絡訓練,得到一系列訓練結果。
4)預測誤差過程必不可少,主要是將檢測數據輸入然后進行模擬輸出,得出相應結果;選取其中立柱結構豎向位移、墻體水平位移、支護樁(墻)頂部豎向位移、支護樁(墻)頂部水平位移和最小的一組結果作為目標最優值。輸入層、隱含層、輸出層的參數設置如表1所示。

表1 網絡訓練參數
優化后形成的模型適應度曲線變化趨勢見圖10,平均適應度曲線呈階梯形快速下降,在反復對模型進行遺傳優化后,個體適應度指標逐漸下降、適應力不斷增強,在進化到第5代時,適應度數值趨于穩定。
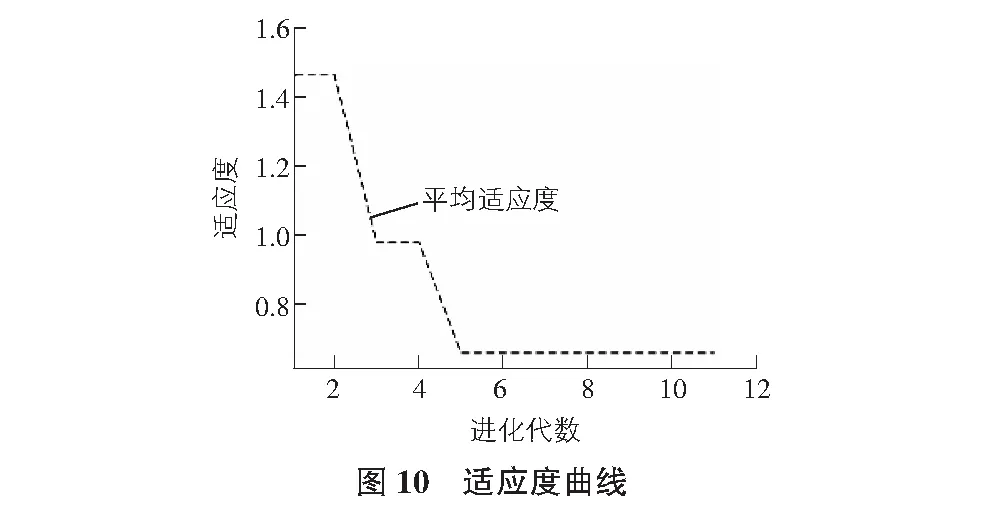
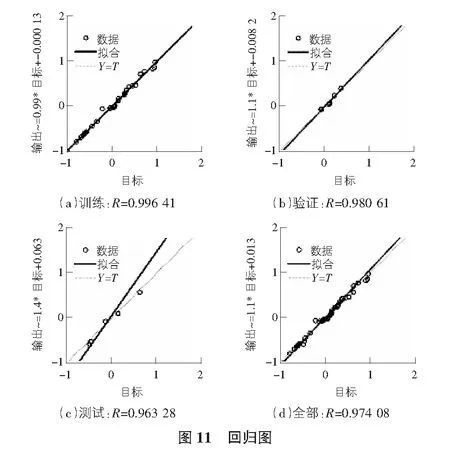
圖11的訓練回歸圖印證了輸入量和輸出量之間極大的相關性,在70%的訓練部分相關系數達到0.996 41,15%驗證相關系數為0.980 61,剩下15%的測試部分相關系數也有0.963 28,總體相關系數值為0.974 08,神經網絡訓練效果優異,為接下來的預測優化奠定基礎。
給每一個變量設置范圍,使范圍同時處在安全值和實測數據之內,采用循環計算的方法,將所有可能的組合輸入到經過訓練的GA-BP神經網絡中,以變量相加得到最小值為最優結果,以此尋找最優地下水位值及其條件。
對神經網絡進行全域搜索,得到的預測值如圖12所示,預測信號和原始信號趨勢基本吻合,經過遺傳算法優化的BP神經網絡得出的K44-280監測點1(右)最優地下水位值為3.852 7 m,達到此最優數值時的條件為立柱結構豎向位移9.1 mm,墻體水平位移2.5 mm,支護樁(墻)頂部豎向位移3.10 mm,支護樁(墻)頂部水平位移19.0 mm,以上數值均在安全范圍內。
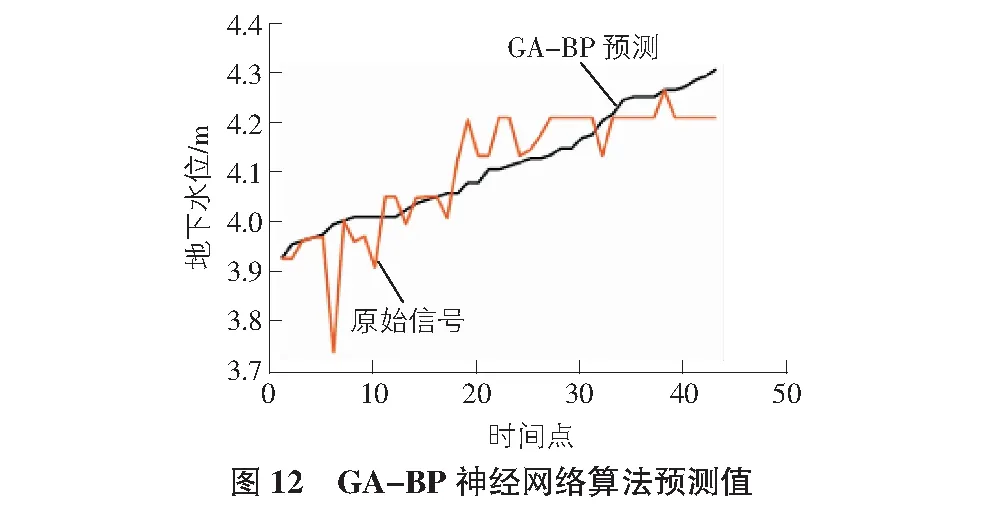
誤差曲線如圖12所示,對比多元回歸方程預測的數值誤差圖如圖13,表2所示。

表2 誤差對比
由圖13可知,基于遺傳算法的BP神經網絡算法具有良好的誤差控制能力,誤差曲線鋸齒狀延伸,整體誤差在±0.1范圍內波動,曲線多元回歸分析曲線在前40 min也呈現良好的誤差表現,變化趨勢與GA-BP神經網絡算法大致相同,誤差震動幅度稍大,峰值超過0.25。
絕對誤差代表了測量值與真實值之間的偏離程度,均方誤差則是度量估計量和被估計量之間的差異程度的值。由表2可知,GA-BP神經網絡算法的絕對誤差均值和誤差均方差均小于多元回歸分析方法,體現了機器學習方法在數據分析上的優勢。
3.2 實驗分析及建議
實測數據表明立柱結構豎向位移、墻體水平位移、支護樁(墻)頂部豎向位移、支護樁(墻)頂部水平位移、地下水位之間有良好的相關性,基于遺傳算法優化的BP神經網絡算法能夠精確預測地下水位最優值,實驗誤差略高于目標誤差,但誤差控制總體處于優良狀態,不影響實驗準確程度,而且通過誤差對比得出相比于多元回歸分析,采用遺傳算法優化的BP神經網絡算法預測效果更好,預測結果更平滑。建議在后續的施工過程中,充分利用神經網絡,深度學習方法,結合施工現場數據,進行更全面、誤差更小的數據分析工作,為后續工程的平穩、安全、高效地向前推進提供數據支撐和保障。
4 結語
本文通過GA-BP神經網絡算法部分的理論分析及基于現場數據的分析仿真實驗,對明挖法市政隧道深基坑過程中的現場數據進行了詳細的分析和預測,并針對后續施工給出了優化意見。研究結論表明:
1)監測數據之間相互影響且影響程度各不相同,其中地下水位與立柱結構豎向位移、墻體水平位移地下水位、支護樁(墻)頂部豎向位移、支護樁(墻)頂部水平位移之間呈現極大相關的非線性變化規律。
2)機器學習方法能夠精確預測地下水位最優值及達到最優時的條件,本文運用基于遺傳算法的BP神經網絡法對地下水位進行預測分析,得到最優結果絕對值為3.852 73 m,此時條件為:立柱結構豎向位移9.1 mm,墻體水平位移2.5 mm,支護樁(墻)頂部豎向位移3.10 mm,支護樁(墻)頂部水平位移19.0 mm,根據城市軌道交通工程監測技術規范[11],均處于安全范圍內。
3)通過誤差對比,揭示了GA-BP神經網絡相比傳統多元回歸分析方法具有更好的預測能力和誤差控制能力,展現了機器學習在工程應用上的獨特優勢。

