一種自適應擾動觀測器的機械手滑模控制研究

馬金茹，高文華，祁宇明

(1.北京電子科技職業學院汽車工程學院，北京 100176；2.天津科技大學，天津 300222;3.天津職業技術師范大學，天津 300222)

0 前言

近年來，機械手發揮著越來越重要的作用，也受到越來越多的關注。對機械手的控制性能要求也越來越高，機械手操作系統的運動控制特性受負載的變化影響比較大，進而使得機械手控制系統特性嚴重下降。

國內外研究學者對機械手控制系統開展了較多的研究，文獻[3]中利用自適應協調控制方法開發了一種用在線參數估計算法來增強的自適應滑模控制器，估計了機器人手臂的質量和轉動慣量等未知物理參數。文獻[4]中研究表明在擾動是有界變差的假設下，基于觀測器控制的閉環系統是輸入到狀態穩定的，不確定性的影響只能衰減到一個特定的水平。文獻[5]中開發出一種SMC方法，假設當時間接近無窮大、擾動導數為零的情況下，通過非線性觀測器處理具有非匹配不確定性的系統，這些觀測器只能用于慢時變擾動，而該假設不適合工程實際。觀測器的增益矩陣是逼近未知不確定的一個重要設計參數。文獻[6]中提出了一種新的自適應機制的觀測器增益矩陣的一般設計方法，但對于多輸入多輸出(MIMO)系統不適用。王炯宇等提出一種基于模糊滑模的交叉耦合輪廓誤差控制方法，通過設計的模糊跟蹤控制器的仿真驗證，表明了該方法能夠提升兩軸伺服系統輪廓的控制精度。王文娟、李俊針對軌跡跟蹤存在隨機干擾等問題，在自適應控制與滑模控制的基礎上，利用徑向基函數(RBF)神經網絡設計了高精度控制律，消弱了滑模控制的抖振現象，通過仿真驗證了所設計的控制律的精確性。陳治提出了一種基于RBF神經網絡的自適應滑模控制算法，仿真結果表明該算法的系統動態誤差小，具有較強的抗干擾能力，能有效解決路由數據傳輸隊列長度的控制。鄭耿峰基于移動機械臂自適應模糊控制和滑模控制方法，提出了考慮未知動力學模型不確定性干擾的控制模型，通過模糊控制來逼近系統以解決參數的不確定性，該模型有效補償了控制器對系統總體參數的不確定性問題，提高了機械臂的軌跡跟蹤性能。邢艷榮等針對四輪全向移動機器人提出了一種自適應滑模控制方法，MATLAB仿真表明:該方法能夠減小系統的抖振，較好地降低了參數變化、外部干擾對機器人軌跡跟蹤的影響。劉樹博等基于機器人多目標擾動觀測器不確定性問題，提出一種滑模自適應控制策略，采用設計多目標擾動觀測器來估計擾動的參數值，仿真結果表明:該算法能夠在給定信號的情況下，有效實現機器人的軌跡跟蹤。

本文作者將進一步探討在明確考慮未知外力的情況下，基于觀測器的機械手跟蹤軌跡控制策略，通過設計一種新的自適應增益算法，提出一種自適應機制的觀測器一般設計方法，在未知恒定負載的情況下，使觀測器狀態達到預計的平衡。該算法將非線性擾動觀測器設計方法擴展至多輸入多輸出系統，且放寬了滑模控制中擾動的邊界假設，能夠有效減輕控制系統的抖振現象。

1 模型化方法

對于個自由度的剛性機械臂，其動力學可以用拉格朗日-歐拉矢量方程來描述：

(1)

1.1 基本控制設計

跟蹤誤差由()=-表示，其中∈表示運動協調中的參考軌跡。設計任務是建立機械手系統的控制律，使得在未知載荷存在時，跟蹤誤差()能夠為零。選取滑動變量：

(2)

其中：是對角矩陣。將方程(2)代入方程(1)得到：

(3)

(4)

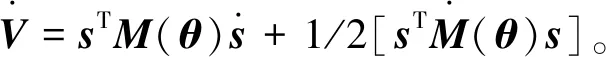
(5)

則基本的滑模控制律可以由下式推導出：

(6)

(7)

為減少抖振，采用連續逼近(+)的方法代替signum函數，其中為較小的正常數，越小，逼近性能越好。為了消除抖振，用飽和函數sat()代替signum函數，然而這個方法的缺點在于原有的魯棒性和控制性能會下降，如降低跟蹤位置精度和增加穩態誤差。另外，由于目標完全未知，不確定度的上界很難得到。當界限沒有完全確定時，方程(6)中的增益需要選得足夠大，較大的增益將導致劇烈的抖動。

1.2 非線性觀測器的設計

在這一小節中，基于文獻[6]設計關于動態方程(1)的自適應非線性擾動觀測器(ANDO)：

(8)

將估計誤差定義為

(9)

根據式(9)，可以得出：

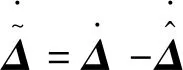
(10)

將方程(1)和(8)代入上述方程，得到

(11)

(12)

可以看出，估計誤差受下式影響：

(13)

引理1:在上述假設成立的基礎上，如果選擇觀測器增益()，使估計誤差系統公式(13)為輸入狀態局部穩定，那么式(14)是漸近穩定的。

(14)

1.3 自適應觀測器增益的設計

引理3:令為Re[()]<0的常數矩陣，那么下式的結論都是漸近穩定：

(15)

如果()在區間[0,∞)上是連續的矩陣函數，則式(16)為常量

(),?≥0

(16)

式中:>0，<0。

證明：如果把方程(15)乘以積分因子et，并且從0到進行積分，得到

(17)

由于Re[()]<0，存在常量<0，>0,使得et≤e，≥0。利用此估計在等式(17)中得出：

(18)

應用Gronwall不等式，得到

(19)

對其進行估計，可以得到

(20)

(21)

對于常數，有()≤e，當為負時，可以得出，當→∞，()→0。即完成了引理2的證明。

方程(8)中觀測器增益()的設計可以用定理1來描述。

定理1：如果方程(8)中的觀測器增益()由下列等式控制，則方程(14)是漸近穩定的。

(22)

其中：和是正常量；是階單位矩陣。

證明：令()表示方程()=η的理論解，從而

()=η

(23)

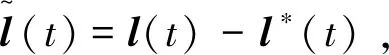
(24)

可以直接從式(22)得到：

(25)

利用公式(22)—(25)可以得到：

(26)

則有：

(27)

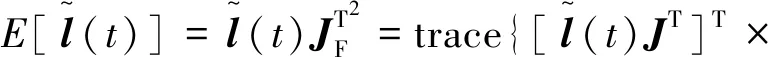
(28)

其中‖·‖是Frobenius范數，則有

(29)

(30)

()=η+e-

(31)

其中：=(0)(0)-η。

由于()全局指數收斂到η，()收斂為η的剩余集。根據引理3，方程(14)是漸近穩定的，即完成了定理1的證明。利用定理1的結果，由引理1導出了估計誤差系統方程(13)為輸入狀態穩定的。

圖1 自適應擾動觀測器增益結構圖

值得注意的是，項可被包括在方程(1)中的，而集中擾動不滿足其導數為定常穩態值的假設：

(32)

即估計誤差不能被逼近到期望的平衡點，對估計誤差的影響將在后面的模擬比較中進行研究。

2 基于自適應非線性觀測器的滑模設計

利用擾動的估計，可以得到定理2中給出的結果。

定理2：假設系統方程(1)滿足假設2和3，根據自適應觀測器增益方程(22)，考慮滑動變量方程(2)和非線性擾動觀測器方程(8)，通過下式所示控制律將機器人系統的狀態驅動到滑模面()=0上：

(33)

其中：>。

證明：考慮到Lyapunov函數

=1/2()

(34)

根據方程(1)的軌跡取導數，得到

(35)

(36)

將等式(4)和(33)代入等式(36)得到

(37)

3 仿真實例與比較

3.1 自適應非線性擾動觀測器的性能

在這一小節中，分析雙連桿機械手的質量發生突變時，所提觀測器(方程(8))的性能特性。假設機械手的未知質量為圖2和圖3所示的形式，觀測器所需參數為=10、=5，參考軌跡由=sin(2)給出。

方程(1)中描述的雙連桿機械手模型如下所示:

()=

(38)

(39)

(40)

未知質量是=[]∈,=。根據參考文獻[14]的研究，線性回歸矩陣和可以寫成：

(41)

(42)

機械手系統參數如下：=0.4 m，=0.3 m，重力加速度取=9.81 m/s。質量標稱值為=2.2 kg，=1.6 kg。

圖2 未知質量Δm1和估計質量 圖3 未知質量Δm2和估計質量

自適應非線性擾動觀測器的性能如圖2和3所示，可以看出即使質量在某些點上發生突變，自適應非線性擾動觀測器的輸出也能及時收斂到實際未知質量和。從這些結果來看，所提出的自適應非線性擾動觀測器提供了對不確定質量變化的有效估計，如圖4所示。

圖4 未知質量的估計誤差

3.2 實驗結果

為了驗證所提出的基于觀測器的滑模控制方法，進行仿真實驗。對于所考慮的單連桿剛性機械臂，其動力學可以用下式描述;

(43)

其中：∈是關節角；單連桿機械臂的參數為：負載臂長度=18.6 cm，負載臂質量=0.225 kg，負載質量=0.298 kg，重力加速度=9.8 m/s。對于所提出的控制律，通過反復試驗來選擇參數，直到獲得更好的跟蹤性能。在模擬中，式(8)中控制參數和觀測器參數=035、=6和=2。在末端效應器處施加未知質量∈。

實驗裝置如圖5所示：伺服基礎單元是齒輪伺服機構系統；負載軸的位置可以使用高分辨率編碼器進行測量；轉速表可以測量馬達的速度；傳感器直接連接到數據采集板，并提供控制連桿所需的位置反饋；數據采集板輸出一個控制電壓，用于放大并驅動電機。

圖5 實驗測試平臺

這里未知有效載荷=0.15 kg，在模擬中被視為未知項。參考軌跡分別由=sin和=sin(2)給出。首先根據圖6和圖7中的等式(8)和(22)分析所提出的非線性觀測器的性能，可以看出估計誤差最終為0.003。即在此研究中所提出的自適應非線性擾動觀測器，通過未知質量的估計來代替不確定性，所設計的自適應非線性觀測器是有效的。

圖6 r1=sint下未知載荷的估計偏差

圖7 r2=sin(2t)下未知載荷的估計偏差

圖8描述了等式(33)中基于觀測器的滑模控制下未知慣性矩的位置跟蹤，該控制器使位置跟蹤誤差為零。基于觀測器的滑模控制為機械手系統產生的有界控制力矩如圖9所示，可以明顯看出基于觀測器的滑模控制在滑模面附近有很小的抖動。這種情況的原因是該觀測器提供了適當的控制增益，以確保跟蹤誤差趨于零誤差。因此，抖振問題得到了有效的緩解。

圖8 自適應擾動觀測器下的響應曲線

圖9 自適應擾動觀測器下控制輸入的響應曲線

綜上所述，所提出的控制方案具有良好的跟蹤性能，適用于快速變化的參考。在觀測器和滑模控制器合理設計的情況下，可以抑制干擾帶來的不利影響。

3.3 實驗分析

為了進行比較，根據方程式(43)分析了參考文獻[15]提出的非線性擾動觀測器的性能，可以得到以下方程：

(44)

其中，集中不確定性=，負載臂長度=19.8 cm。根據參考文獻[15]，對于動力學方程(44)，相應的觀測器重構如下：

(45)

為了研究觀測器方程(41)對不同頻率擾動的精確估計問題，用下列被測擾動代替方程(44)中的不確定度。

情況1：=sin(02)

情況2：=sin(06)

情況3：=sin

情況4：=sin(2)

最大估計誤差的變化規律如圖10所示，是擾動的估計誤差，可以看出:最大估計誤差隨干擾頻率的變化而變化，估計精度主要取決于干擾頻率，擾動的頻率主要是由這種變化引起的。與參考文獻[15]相比，所提觀測器在這方面具有明顯的優勢。

圖10 非線性擾動觀測器估計誤差的比較

對于基本滑模控制律來說，一般通過試錯法選擇控制器參數，直到獲得更好的跟蹤性能。為了評價控制器的性能，跟蹤誤差平方積分()和控制力矩平方積分()等指標考慮如下：

(46)

所有情況下均選擇=30 s，表1為控制器的性能指標，圖11為基本滑模控制律控制輸入的響應曲線，可以看出由于開關增益較大，控制器產生了較大的抖動。此外，性能指標僅在0.001 3～0.003 5之間變化，而性能指標從671.190 7 N·m下降到582.435 6 N·m。結果表明：這兩種方法在控制效率方面取得了相似的效果；存在未知有效載荷的情況下，通過自適應非線性擾動觀測器估計擾動，可以有效地減少抖振的出現。

表1 控制器的性能指標

圖11 基本滑模控制律下控制輸入的響應曲線

4 結論

針對機械手目標捕獲等操作任務，提出了一種基于觀測器的滑模控制。為了提高系統性能，設計了一種新的自適應非線性觀測器，用于逼近機械手的未知載荷引起的不確定性，建立了魯棒觀測器增益矩陣的一般設計方法，并將基于觀測器的滑模控制的適用范圍擴展到一些工程問題。該觀測器克服了現有非線性擾動觀測器的一些限制。對于未知載荷的機械手，將滑模控制與觀測器相結合，得到了漸近穩定結果。最后，通過兩個算例驗證了所提出的自適應非線性觀測器和基于觀測器的滑模控制方法的有效性。仿真結果表明：所提出的基于觀測器的滑模控制方法是有效的。