基于模擬優化模型的渠井結合灌區多目標水資源優化配置

王芊予，胡天林，芮松楠，褚夢喬，降亞楠，2

（1.西北農林科技大學水利與建筑工程學院，陜西 楊凌 712100；2.西北農林科技大學旱區農業水土工程教育部重點實驗室，陜西 楊凌 712100）

0 引 言

水是糧食生產和社會經濟發展不可替代的寶貴資源，伴隨著生活水平的提高和飲食結構的變化，我國對優質農產品的需求不斷增加，導致農業用水量不斷增加。受我國水資源宏觀稀缺的約束，經濟社會的高速發展和人口數量的不斷攀升導致工業用水不斷擠占農業和生態用水，部分地區農業用水矛盾突出[1]。尤其在氣候干燥、降水稀少的西北地區，有限的地表水資源難以滿足灌溉用水的需求，因此常采用井灌來補充灌溉，形成了典型的渠井結合灌溉模式，實現了地表水和地下水的聯合利用，提高了灌溉用水保證率，涵養了寶貴的地下水資源。但近年來由于地區性降雨較少，上游河流開發力度加大以及引水工程的老化失修，導致灌溉引水量不斷減少，地表水用水保證率無法得到保障，再加之井灌的靈活性、便捷性和經濟性，部分農戶轉向采用地下水進行灌溉，導致地下水過量開采，渠井用水比例失調[2]，灌區渠灌用水下降，地下水補給量減少而無法得到有效涵養，地下水水位持續下降，形成了地下水降落漏斗[3]，機井出水量下降、灌溉時間和抽水能耗激增，甚至機井報廢。傳統的灌區水資源配置沒有與地下水數值模擬模型進行緊密耦合，因此對灌區水文地質條件、種植結構的空間分布考慮不足，容易導致灌區地下水開采總量不變，但地下水局部超采的現象，不滿足地下水管理條例[4]提出的取水總量和地下水位雙控指標。因此亟需構建基于模擬優化模型的水資源優化配置模型，將地下水數值模擬模型與優化算法進行耦合，充分考慮研究區的水文地質情況、邊界條件，補給、徑流和排泄的時空分布特性，采用數值模擬模型對灌溉條件下的地下水的時空動態進行模擬，最終得到空間分布的模擬結果，進一步提高渠井結合灌區水資源配置的合理性，促進灌區灌溉用水方式由粗放低效向節約集約的精細化管理轉變[5]。

當前的水資源優化配置常考慮經濟、生態、社會等多方面目標。邵東國[6]等通過考慮生態環境保護、水權轉讓、利益補償等因素，在滿足人們生存、工程供水能力，用水公平性的基礎上，構建了水資源凈效益最大的目標函數，并采用水資源系統的熵變關系對水資源配置進行合理性評價。付銀環[7]等基于區間兩階段隨機規劃的方法，以灌區用水成本最小為目標結合作物水分生產函數，建立了不確定性的水資源優化配置模型。粟曉玲[8]等以生態、經濟綜合效益最大為目標建立單元種植結構優化模型，再利用水資源轉化模擬模型對結果進行求解，實現了先優化后模擬的模擬優化松散耦合模型。Farhadi[9]等以灌溉缺水量最少，水量分配公平度最大和地下水下降最小為目標，將MODFLOW 求解出的分配方案作為數據訓練集，進而構建基于神經網絡的多目標優化模型并結合納什議價模型進行方案選取。綜上，在目標的量化方面，目前研究大多通過貨幣價值衡量水資源價值，而忽略其社會屬性、環境屬性和公有性[10]，當前盡管有部分模型在選取配置方案的過程中考慮了行政區間配水的公平性問題，但針對渠井結合灌區考慮用水公平度的模型較少，在實際應用中不利于灌區的統觀統管，在我國種植結構受政府政策、市場和政府引導的大背景下，在水資源配置中需要充分考慮特色名優經濟作物的用水特點，也應保證糧油等作物的用水需求，進一步提升水利對地方特色經濟的推動作用，因此有必要在水資源配置中進一步考慮各區域的配水公平性。

隨著計算機領域的優化算法和水資源模型理論的高速發展，水資源模擬優化模型的研究日益深入。譚倩[11]等人將魯棒規劃的多目標方法引入水資源優化研究中，建立基于魯棒規劃方法的農業水資源多目標優化配置模型（MRPWU 模型），通過引入保護函數和非線性保護函數線性化的方式有效處理雙目標規劃中權重的不確定性。邵東國[12]等通過構建AquaCrop 作物模型，對不同作物的產量與灌排關系進行模擬計算，以水稻產量、灌水量、排水量為優化目標，提出基于AquaCrop 模型與熵值法耦合的多目標多情景優化方法。孫月峰[13]等人采用混合遺傳模擬退火算法建立了以經濟、社會和環境的綜合效益最優為目標的優化配置模型，有效提高了求解速度和解的精度。楊蘊[14]等人將基于過渡帶理論的海水入侵變密度流數值模擬程序SEAWAT 同遺傳混合算法NPTSGA 相耦合，開發了海水入侵條件下地下水多目標模擬優化管理模型，以實現多重管理的目標。傳統水資源多目標模擬模型的優化方法采用目標加權法、距離函數法或最小最大準則將多目標問題轉化為單目標問題進行求解[15]，但由于權重和需求水平的高敏感性使得解集的優劣性無法得到保證。而現階段的優化方法也可以耦合數值模擬模型進行求解，但多采用松散耦合的方式，雖然提高了結果的合理性和可行性，但采用的耦合方式使得計算機內存在優化算法和模擬模型之間無法快速的共享數據，極大地降低了計算速度和求解效率[16]。緊密耦合的模擬優化模型可采用統一的編程語言把優化算法與數值模擬模型進行緊密耦合，將數值模擬模型計算的分布式結果作為目標函數值，極大地增強了目標函數對空間信息的提取能力，也可將空間分布的約束條件施加到相應的位置（單元格）上，在空間上對地下水的開采進行調控。目前研究中采用的多目標優化算法如蟻群算法[17]、粒子群算法[18]、NSGA-II[19]等啟發式算法，在處理多個目標（5 個及以上，Many-Objective Optimization）函數時搜尋能力較低，采用專門針對多目標改進的NSGA-III算法的研究較少。

基于此本研究從一個假想算例著手，基于Python 語言將優化框架Pymoo 中的NSGA-Ⅲ算法與地下水數值模擬軟件包FloPy 進行緊密耦合，通過編寫模塊化目標函數建立典型渠井結合灌區的多目標水資源配置模擬優化模型，以探索經濟效益、區域配水公平、地下水可持續利用等多個目標對配置方案的影響，同時給決策者提供基于不同偏好和基于博爾達計數規則確定的兩類水資源配置方案，為灌區地表水地下水可持續安全高效利用，地下水取水總量和地下水水位雙控提供強有力的技術支撐。

1 研究方法

1.1 地下水數值模擬模型

MODFLOW 是由美國地質調查局采用有限差分法開發的用于孔隙介質中三維地下水流模擬的模塊化數值模擬模型軟件[20]，由一個主程序與若干相對獨立的子程序包組成，通過定義子程序（補給、河流、井、排水等）中的相關模塊進行數值模擬過程。鑒于其顯著的模塊化結構，Bakker[21]等人基于Python編寫了地下水數值模擬FloPy庫。

由于灌區承壓水開發利用程度較低，資料匱乏，目前灌溉主要開發利用潛水，且淺層地下水以垂向運動為主，故將研究區潛水水流系統概化為均質各向同性二維非穩定流單層潛水含水層，地下水流數學模型[22]如下：

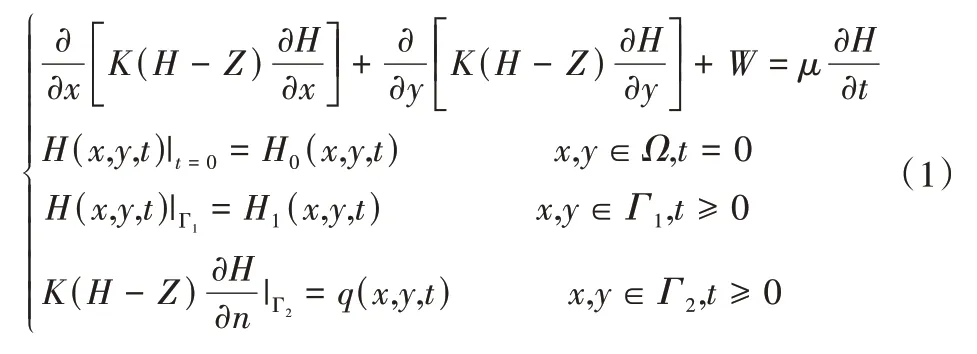
式中：K為潛水含水層滲透系數，m/d；H為潛水水位，m；Z為含水層底板高程，m；W為源匯項，m/d；μ為潛水含水層給水度；t為時間，d；Ω為計算區域；x,y為坐標；Γ1，Γ2為第一、二類邊界；q(x,y,t)為流量邊界單寬流量，m2/d。

本研究通過調用FloPy 中相應的子程序包基于上述數學模型定義并修改含水層網格、水文地質參數、初始條件、邊界條件等方面，通過自定義灌區補給項（包括降雨、田灌入滲、井回歸補給等）和灌區排泄項，開發、運行精細化模型并讀取分析結果。

1.2 多目標遺傳算法NSGA-Ⅲ

多目標問題的傳統求解方法是通過加權或約束折衷等方法將多目標優化問題轉化為單目標優化問題，當需獲得多個不同解決方案時只能通過重復應用模擬來實現，而進化算法能夠在一次模擬運行的過程中找到一系列帕累托最優解集，非支配排序遺傳算法（NSGA）則是最早的進化算法之一。由于在排序過程中出現計算復雜度較高、易丟失良好解決方案和需提前設定共享參數的問題，Deb[23]等人提出改進的非支配排序遺傳算法（NSGA-Ⅱ），通過快速非支配排序的方法降低計算復雜度，引入精英策略以增大采樣空間，提出擁擠距離代替共享參數，以保證種群在進化過程中的多樣性。隨著優化目標數量的進一步增多，求解出的非支配個體在種群中的占比呈指數型上升，非支配解集的收斂性顯著下降，為保證多樣性而引入的擁擠距離算子計算代價增加，為解決以上問題，Deb 和Jain[24,25]進一步提出基于參考點的第三代非支配排序遺傳算法（NSGA-Ⅲ），采用邊界交叉構造權重的方法產生參考點，在臨界層的環境選擇中通過預定義多個分布良好的參考點以維持種群的多樣性，修改精英選擇算子和后代種群以求解一般約束的多目標優化問題，有效解決了高維目標優化問題中的解集收斂性問題。

2 模擬優化模型的構建

2.1 數值模擬模型的構建

康燕楠[26]等在對西北典型渠井結合灌區寶雞峽灌區調研的基礎上，綜合灌區的實際情況設計了一個灌溉設施完善包含不同水文地質分區的典型灌域，該灌域僅采用渠灌或井灌均可滿足灌溉要求，長5 km，寬3.5 km，在空間上剖分成50 行50 列的長方形網格，東西邊界概化為定水頭邊界，南北邊界概化為零流量邊界，灌域內共設置50 眼抽水井，具體見文獻[26]。本文在此基礎上，根據不同作物種類將灌區在空間上劃分為5 個種植區域，同時基于行政管理的考慮將灌域劃分為5個行政分區，通過行政分區1、5 和2、3、4 不同的地下水埋深來模擬灌區塬上和塬下兩個灌溉系統，在各行政分區設置一口觀測井以便監測地下水位，渠井結合灌域的模型示意圖如圖1所示，相關水文地質參數參考鄧康婕[27]根據涇惠渠灌區成果報告等資料確定，種植結構與灌溉周期[28-30]如表1和表2所示。

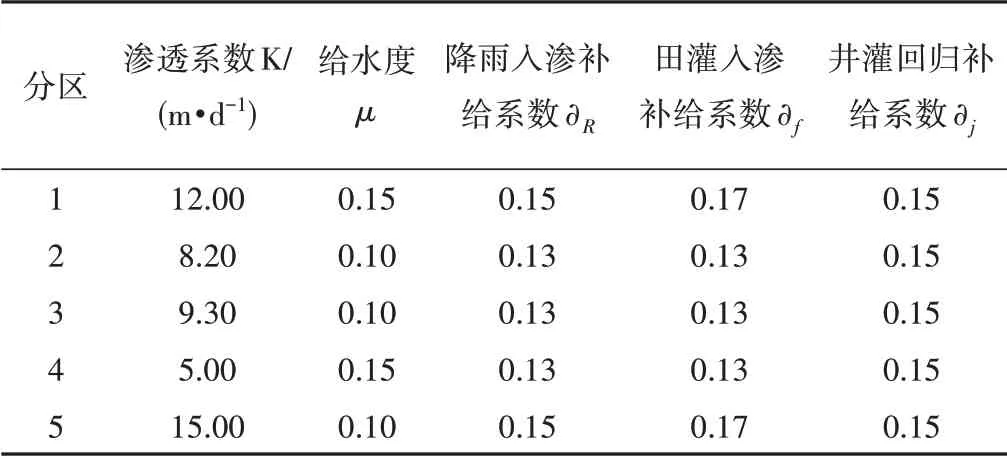
表1 水文地質參數表Tab.1 Hydrogeological parameters of the case study

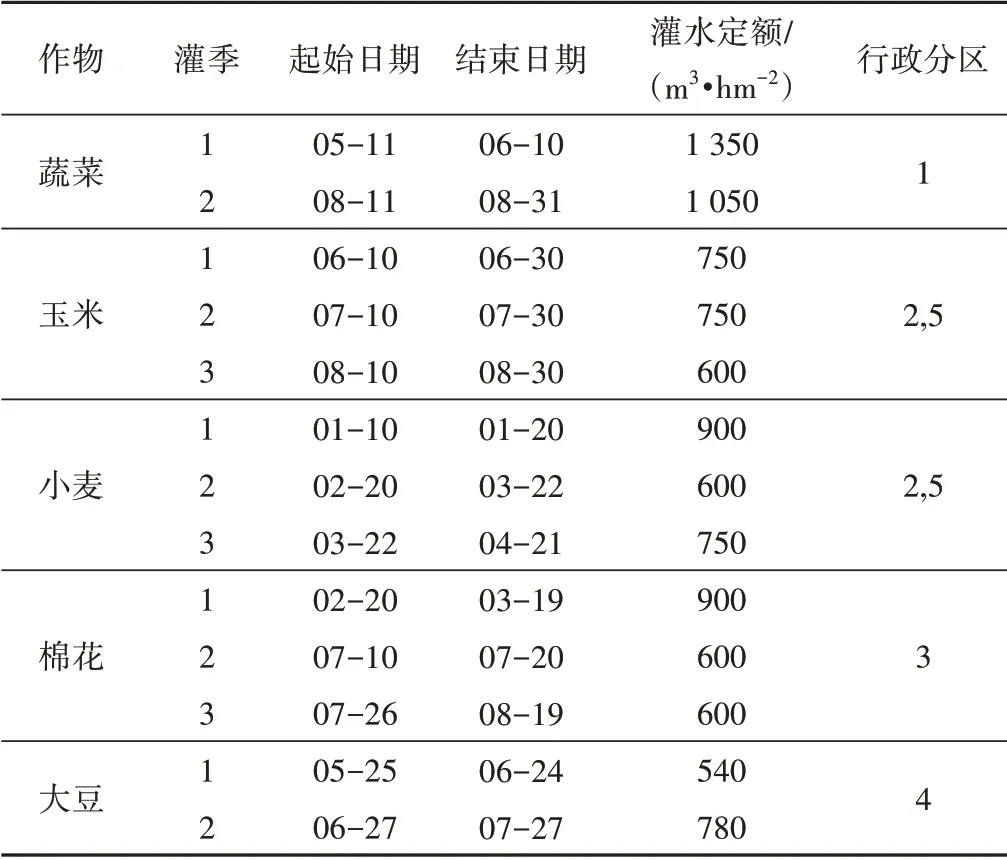
表2 種植結構與灌溉制度表Tab.2 Crop patterns and irrigation schedule

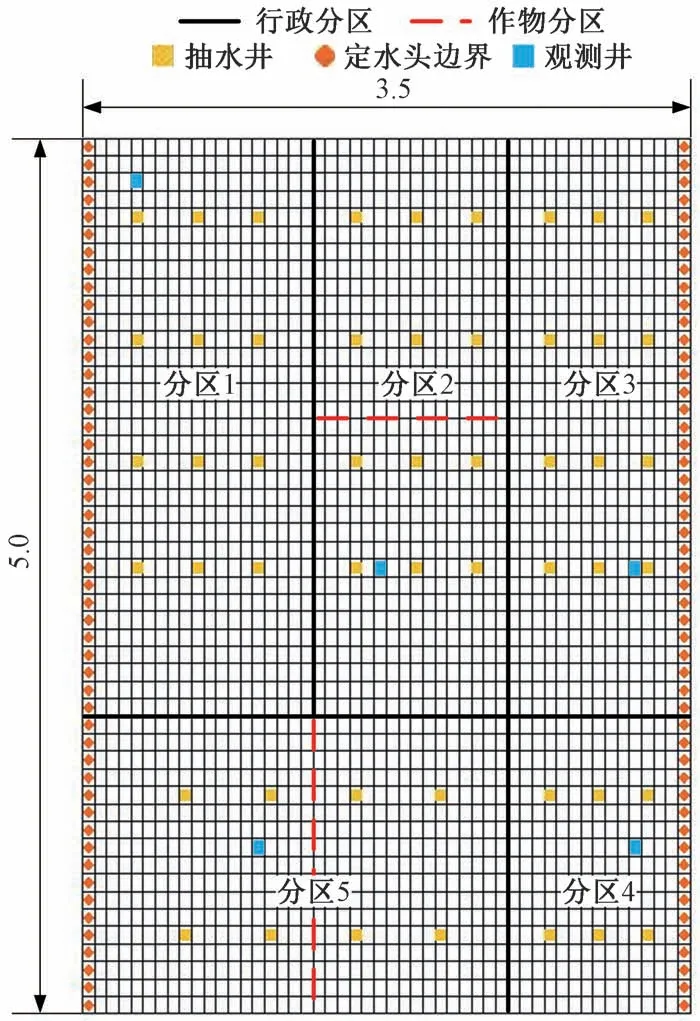
圖1 典型灌域示意圖（單位：km）Fig.1 A diagram of geological model of typical irrigation area

本文使用FloPy 構建MODFLOW 模型，首先導入FloPy 并創建一個MODFLOW 的模型對象；利用FloPy 中的Dis 程序包創建含水層，設定應力期和計算時間步長為默認值1d；采用FloPy 中的Bas 程序包模擬活動單元格的屬性并設定初始水頭值、Lpf 程序包對含水層的水力特性與類型進行定義、Ghb 程序包對含水層的邊界條件進行設定、Rch 程序包將降雨入滲、田灌入滲和井回歸補給給地下水、Wel程序包通過輸入的抽水井位置、抽水速度和應力期對含水層的井開采情況進行模擬；最后調用Sip 求解器進行求解并使用Oc 程序包對MODFLOW模型的輸出頻率和類型進行定義。

2.2 優化模型

2.2.1 決策變量

本文針對五種作物分別考慮其灌溉用水量與渠井用水比例，因此共設置10 個決策變量，分別為PCWi、Fi，其中：PCWi為各作物用于灌溉的渠井用水比例；Fi為分配給各作物的灌溉用水量，m3；i為作物種類數量。以各作物在不同灌季不同灌水定額的比例為依據，將各作物的渠灌用水量與井灌用水量在不同灌季進行分配，根據作物種植結構與行政分區進行空間劃分，以模擬灌溉水入滲補給，包括渠灌回歸、井回歸補給和地下水灌溉開采情況。

2.2.2 目標函數

灌區水資源優化配置是一個涉及多方利益主體的復雜問題，因此本文在選擇優化目標時，通過引入灌區凈經濟效益最大目標以滿足農戶需求，設置地下水平均累計下降變化最小目標以滿足生態和地下水管理的可持續發展要求，考慮缺水量最小目標以滿足作物生長發育要求，設置各行政區配水公平度和用水效率最大目標以滿足管理者實行配水方案的需求。

（1）經濟效益目標。灌區內用水產生凈效益最大，即：

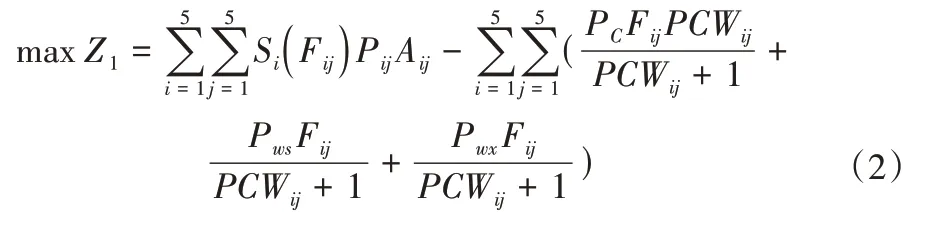
式中：Z1為灌區用水總凈效益，元；i,j分別代表作物類型編號與行政分區編號；Fij為各作物在各行政區的灌溉用水量，m3；PCWij為各作物在各行政區用于灌溉的渠井用水比例；Pij為各作物在各行政區的單價，即蔬菜、夏玉米、冬小麥、棉花、大豆的單價分別為3.9、3.4、3.2、7.0、2.4 元/kg；Aij為各作物在各行政區的面積，hm2；Pc為渠道引水灌溉的價格，0.27 元/m3；Pws和Pwx分別為塬上塬下抽水灌溉的價格0.16 和0.11 元/m3；Si為不同作物產量與灌溉量的具體關系。

通過查閱作物耗水量與產量相關關系文獻[31-34]，得出如下公式：

式中：S1、S2、S3、S4、S5分別為蔬菜、夏玉米、冬小麥、棉花以及大豆的產量函數，kg/hm2；Q1、Q2、Q3、Q4、Q5分別為蔬菜、夏玉米、冬小麥、棉花以及大豆的全生育內的灌溉水量，m3/hm2。

（2）單元格地下水位平均累計下降變化目標。灌區單個網格每日地下水位較前一日的下降年累計值最小（不考慮地下水位上升的情況），即：

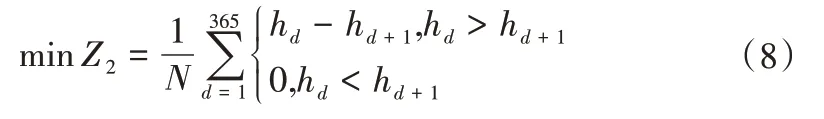
式中：Z2為單個網格的年累計下降值，m；N為灌區在空間內劃分的總網格數；hd為灌區內各網格每日地下水位之和，m。

（3）缺水目標。各作物需水量與灌溉用水量之差最小，即：

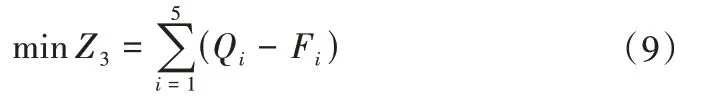
式中：Z3為各作物的缺水量之和，m3；Qi為灌區各作物在概化模型中的最大灌溉需水量，m3。

（4）公平度目標。塬上與塬下的各行政分區灌溉用水量與需水量比值差異最小，即：

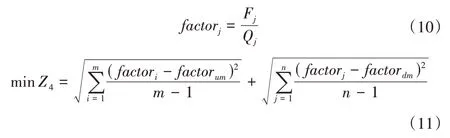
式中：Z4為灌區塬上塬下公平度之和，公平度目標值越小表明越公平；m,n為塬上、塬下行政區數；factorj為各行政區的公平度因子；factorum為塬上各行政區公平度因子的均值；factordm為塬下各行政區公平度因子的均值。

（5）用水效率目標。各行政區內不同作物總產量與總分配水的比值最大，即：

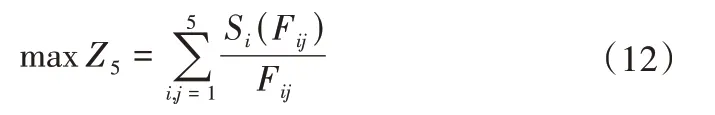
式中：Z5是灌區總用水效率之和；Si為各作物產量與需水量的函數關系。

2.2.3 約束條件

為保持地下水采補平衡以及灌區用水特點，考慮約束如下：

（1）供水能力約束：

式中：Wi為用于灌溉各作物的地下水開采量，m3；Ci為用于灌溉各作物的渠灌量，m3；Wmax,i為種植各作物行政區內的所有井的開采能力之和，m3；Cmax,i為種植各作物行政區內的渠道輸水能力之和，m3。

令布爾變量μ(pi,kα)表示協同成員pi與知識點kα間是否存在關聯關系。協同成員pi與知識點kα間存在關聯關系，即協同成員pi掌握知識點kα，則μ(pi,kα)=1；反之，則有μ(pi,kα)=0。因此，K-K子網絡與P-P子網絡之間的映射關系可以表示為

（2）需水量約束：

式中：Fmin,i為各作物所分配用于灌溉的最小水量值，m3，本文取枯水年灌溉定額的60%，Fmax,i為各作物所分配用于灌溉的最大水量值，m3，本文取枯水年的灌溉定額。

（3）渠井用水比例約束：

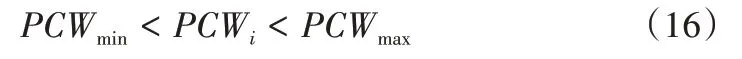
式中：PCWmax為使寶雞峽灌區地下水位抬升兩米的最大渠井用水比例；PCWmin為使寶雞峽灌區地下水位降低兩米的最小渠井用水比例，參考寶雞峽灌區渠井用水比例對地下水位影響的相關研究[35]，取PCWmax為1.97，PCWmin為0（即全井灌）。

（4）非負約束：

式中：Wi為用于灌溉各作物的井灌量，m3；Ci為用于灌溉各作物的渠灌量，m3。

2.3 模擬優化模型

優化問題中灌區總經濟效益目標通過調用灌溉水量—產量函數對個體進行遍歷計算得出對應目標結果；灌區地下水位平均累計下降變化目標需調用2.1 中基于FloPy 構建的MODFLOW 地下水數值模擬模型對其輸出的水頭數據進行處理得到所需目標結果；缺水量目標則可通過決策變量間的簡單計算得出相應目標結果；公平度目標可根據塬上塬下不同行政分區的基本數組運算得出；用水效率目標可基于各行政區的經濟效益與用水量進行數組運算求解，采用外部耦合的方式，將各優化目標以目標函數的形式內嵌至優化模型中，通過決策變量在模擬模型和優化模型間進行參數傳遞，不斷重復調用優化問題中的目標函數和約束條件，使用NSGA-Ⅲ算法進行優化求解。優化問題部分將模擬模型內嵌進目標函數，優化求解則通過不斷調用優化問題計算目標函數值和約束條件實現模擬模型和優化模型的緊密耦合，具體耦合過程如圖2所示。

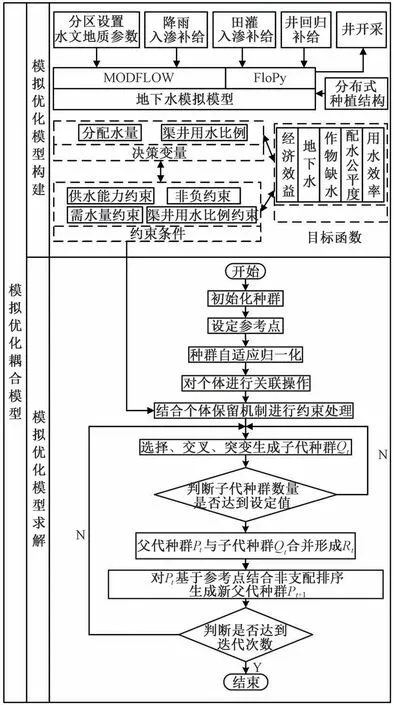
圖2 模擬優化緊密耦合流程圖Fig.2 Tightly coupled simulation optimization flowchart

3 結果與分析

3.1 參數設置與模型評價

NSGA-Ⅲ參數設置：參考方向采用Das-Dennis 方法，分區數partitions=5；選擇空間隨機采樣、隨機選擇方式；取用模擬二進制交叉和多項式突變，其中交叉率Pc= 0.73，變異率Pm= 0.05；種群大小popsize=130，優化搜索代數generation=100。

將采用模擬優化模型求解出的Pareto 解集使用Hypervolume 指標[36]（表示解集中的個體與參考點在目標空間中所圍成的超立方體體積）進行評價，該指標可以有效評價解集的收斂性、均勻性以及廣泛性，同時當Hypervolume 指標達到最大時表明該解集收斂至Pareto 最優[37]。經過反復調試，最終選取參考點（40.34，-14 045 971.15，5 777 949.98，1.019，-0.05）并計算得出相應的Hypervolume 指 標。Hypervolume指標見圖3，算法在50代左右達到收斂。

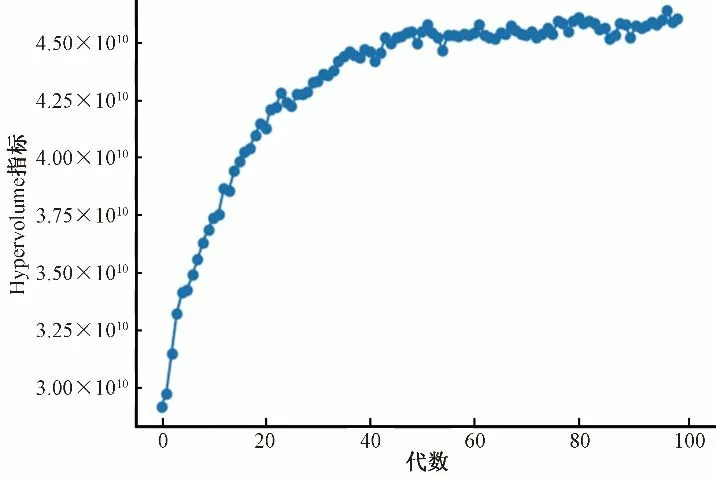
圖3 Hypervolume指標Fig.3 Hypervolume indicator

3.2 基于不同偏好的配置方案選擇

由于模擬優化模型各優化目標間的排斥性，無法得出唯一的全局最優解，而是得到一系列的非劣解集。求解得出的非劣解共57 組，五目標對應Pareto 非劣解集見圖4（其中散點尺寸越大代表該目標方案缺水量越大，顏色接近紅色代表該目標方案經濟效益越高，顏色越接近藍色代表該目標方案經濟效益越低）。

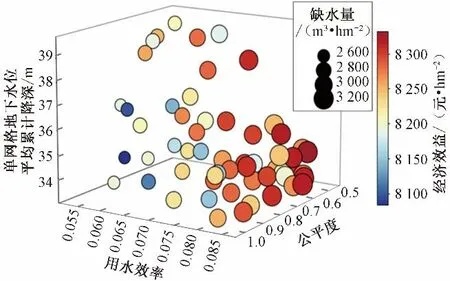
圖4 配置方案Pareto解集空間分布圖Fig.4 Spatial distribution of Pareto front

為方便決策者進行方案選擇，本研究分別選取灌區經濟效益最高、地下水位平均累計降深最小、缺水量最小、公平度最大和用水效率最高5個不同偏好的典型方案進行分析，各不同偏好方案見圖5（圖中各目標函數值經極差標準化處理，為避免標準化后目標函數值出現0值，故對標準化后各目標值加0.5），具體目標值如表3所示。

表3 5個不同偏好典型方案的目標值Tab.3 Typical plan values of five different allocation plans

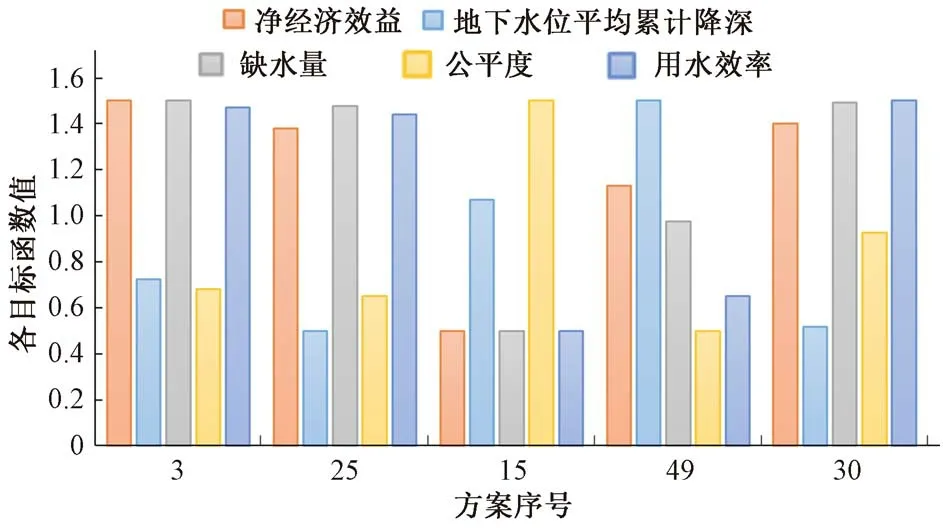
圖5 各不同偏好方案柱狀圖Fig.5 Objectives values of different allocation plans

在5 個不同偏好的典型方案中，方案3 經濟效益最高，但缺水量相較均值高11.27%，不利于灌區作物的生長發育；方案25 單網格地下水位平均累計下降變化最小，對灌區地下水的安全利用最有利；方案15 缺水量最少，但經濟效益相較于均值而言低0.61%，公平度相較于均值而言低16.42%，用水效率相較于均值低26.76%，不利于灌區配水方案的實施和經濟的可持續發展；方案49 公平度最高，但單網格地下水位平均累計下降相較于均值而言高10.76%，用水效率相較于均值低19.72%，雖對灌區配水方案的實施最有利，但不利于灌區整體的高效發展；方案30 用水效率最高，但缺水量相較均值而言高11.06%，影響灌區作物的產量。

綜上所述，以上5個目標間存在相互排斥關系，某一目標最優勢必要犧牲其余目標值，決策者可以根據自己的偏好目標進行方案選擇，若需要提高經濟效益則選擇方案3，若偏好保護地下水則選擇方案25（雖渠井用水比例中井灌用水占比較多，但實際灌溉用水量較少，即對地下水抽取總量較少），而若側重灌區作物的生長發育情況則選擇方案15，若想要更好推進配水方案的實施則選擇方案49，若提倡用水的高效性則選擇方案30，各方案對應的灌溉用水量、渠井用水比例見表4。

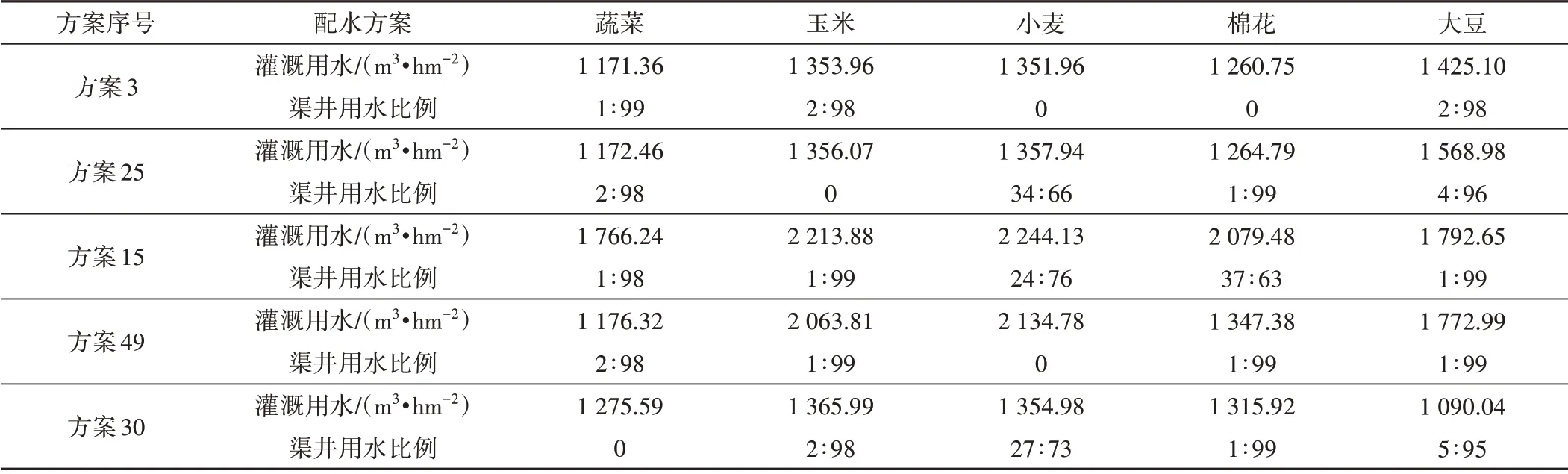
表4 5個不同偏好典型方案的灌溉用水量和渠井用水比例Tab.4 Water distribution and water used proportion of five different allocation plans

3.3 基于博爾達計數規則的配置方案選擇

灌區水資源配置問題是一個涉及多因素影響的復雜過程，單純追求某一因素最優而忽略其他方面是不夠合理的，應充分考慮各目標的實際情況，綜合選取決策方案。故本文基于博爾達計數規則[38]，針對不同目標對配水方案進行打分賦值，分數從1 到m，對應目標函數值最優的方案得到m分，目標函數值最劣的方案得到1 分，最終將各方案的目標分數值累加，取得分最高的方案作為最優方案。該計數規則更多地考慮各目標的綜合影響，避免對不同目標不同偏好引起的投票悖論，充分考慮各目標的偏好信息，具有一致性和共識性，各方案總得分情況如圖6所示。

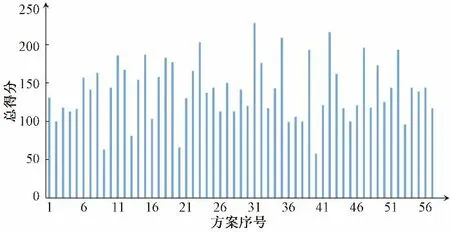
圖6 各方案得分Fig.6 Final score of each pareto front

最終選擇得分較高的前三名作為最優方案（見表5和圖7，其中圖7中各數據經極差標準化處理后加0.5），其中方案31的經濟效益增加0.14%，單元格地下水平均累計下降變化低4.49%，用水效率高16.9%，缺水量低0.15%，但公平度低52.2%；方案42 的單元格地下水平均累計下降變化低3.35%，公平度高8.96%，用水效率高15.49%，但經濟效益低0.54%，缺水量高5.83%；方案35 的單元格地下水平均累計下降變化低4.32%，公平度高1.49%，作物缺水量低5.21%，但用水效率低14.08%，經濟效益低0.08%（以上變幅均基于均值進行比較）。

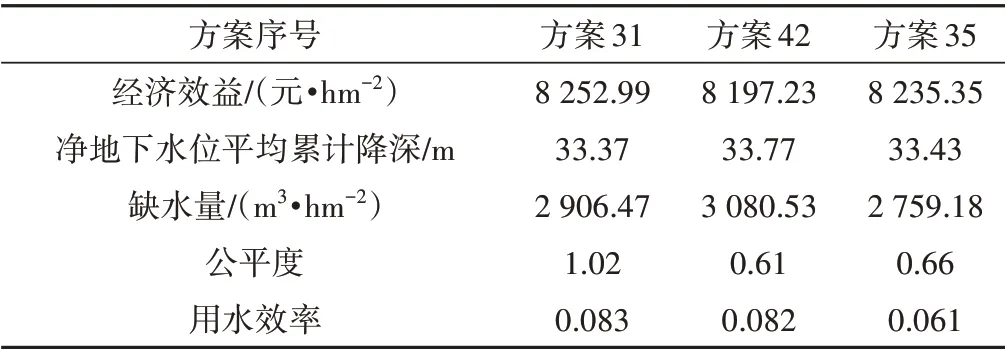
表5 基于博爾達計數規則的最優方案Tab.5 Best solutions chosen acquired based on Borda count

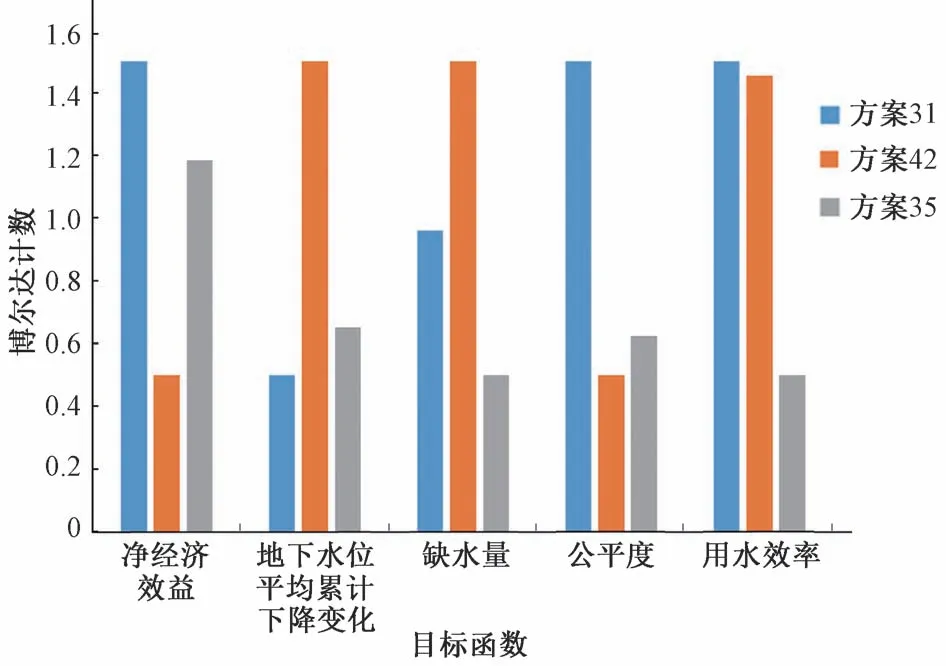
圖7 3個最優方案對比Fig.7 Comparison of three optimal solutions

取博爾達最優水資源配置方案31 的地下水位變化趨勢（圖8）進行分析，各個行政分區的地下水位隨降水和灌溉開采變化明顯，分區1年地下水位變幅不超過0.5 m，分區2年地下水位變幅不超過2 m，分區3年地下水位變幅不超過0.5 m，分區4年地下水位變幅不超過1 m，分區5年地下水位變幅不超過0.5 m。

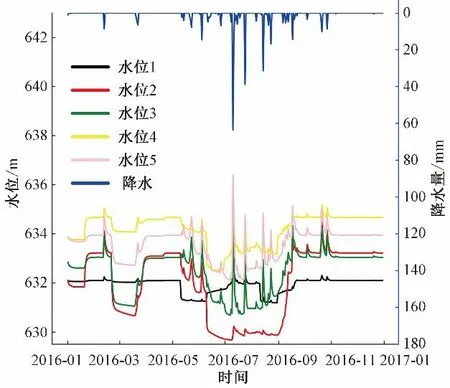
圖8 博爾達最優配置方案各分區觀測井地下水位變化趨勢Fig.8 The changing trend of groundwater level for each observed wells based on Borda count

綜上所述，若決策者對經濟效益、地下水可持續發展、用水效率以及缺水量四方面較為重視，而對配水公平度要求程度較低，則選取方案31；若決策者傾向配水公平度較高而對作物缺水量要求程度較低，則選取方案42；若決策者對用水效率要求程度較低，可選取方案35，基于博爾達計數規則選取的各方案對應的渠灌、井灌用水量見表6。

表6 基于博爾達計數規則選取方案的渠灌和井灌用水量m3/hm2Tab.6 The amount of canal and well irrigation water based on Borda count selected solutions

4 結論與討論

本文基于Python 語言構建了一個緊密耦合的渠井結合灌區多目標水資源配置模擬優化模型，充分考慮降雨入滲補給，地表水灌溉下滲補給地下水，井灌開采抽取地下水以及井灌回歸補給地下水等水循環環節，同時結合經濟效益、地下水水位平均下降變化、農作物缺水程度、各行政區域配水公平度和用水效率5 個目標，并采用NSGA-Ⅲ算法進行了優化求解。

根據優化求解的結果，本文提供傾向于不同目標的配水方案，若偏好全年的經濟效益最高，灌區蔬菜、玉米、小麥、棉花、大豆渠井用水比例分別為1∶99、2∶98、0、0、2∶98；若傾向維持地下水的可持續發展，灌區五種作物的渠井用水比例分別為2∶98、0、34∶66、1∶99、4∶96；若要保證作物的生長發育，灌區五種作物的渠井用水比例分別為1∶98、1∶99、24∶76、37∶63、1∶99；若要強調各行政區配水量的公平性，灌區五種作物的渠井用水比例分別為2∶98、1∶99、0、1∶99、1∶99；若要關注行政區用水的高效性，灌區5 種作物的渠井用水比例分別為0、2∶98、27∶73、1∶99、5∶95。

同時本文也提供基于博爾達計數規則綜合考量的配水方案，最終選擇3 個最優方案，其中博爾達最優方案對應的蔬菜、玉米、小麥、棉花、大豆的渠灌、井灌用水量分別為19.5、1 930.35；68.34、1298.41 m3/hm2；641.49、723.39；83.91、2 013.87 m3/hm2；533.08、554.84 m3/hm2,決策者可以根據當地的實際情況進行決策。

本文通過考慮行政區劃的配水公平度和用水效率模擬決策者的配水過程，使得模型的模擬結果更易于實際應用，通過調整渠井用水比例和灌溉水量來進行水資源優化配置，為灌區水資源配置提供了新的參考依據。但本模型僅基于一個假想案例，未采用連續多年資料進行多年調節，在考慮作物產量—耗水量關系時也并未采用目前通用的AquaCrop 作物模型[39]進行緊密耦合，同時并未分區約束地下水水位以及考慮地下水補償價格的影響，因此在后續的研究中可進一步將上述不足納入考量并基于真實灌區構建模型。此外也可以采用不同優化算法進行求解，橫向對比在各目標情況下不同算法的性能情況和求解結果的優劣性，以實現配水方案更為精準的管理。