基于改進雙卡爾曼濾波法的儲能電池SOH 估計

左 信 陳志鵬 岳元龍

（中國石油大學（北京）信息科學與工程學院自動化系）

儲能電池及以它為核心的不間斷電源系統（Uninterruptible Power Supply，UPS），對鉆井平臺作業的可持續性和安全性有著重要作用。 健康狀態（State-of-health，SOH）用來評估電池的老化程度， 是影響電池供電性能和安全運行的關鍵因素，SOH低于80%的電池應該及時更換。目前公認的SOH測量方法為全容量核對性測試方法，但因測試過程放電時間過長、深度過大，無法滿足運營需求。 因此，進行儲能電池SOH估計方法的研究是非常必要的。

目前對SOH估計的研究方向大致可分為數據驅動［1，2］和模型研究［3］。 數據驅動建模使用統計理論或機器學習技術直接從觀測數據中推導出數學模型［4］，不足或有偏差的訓練數據可能導致估計不準確。 模型研究常采用等效電路模型，即采用簡單的電路元件組合的方式來模擬電池的電化學行為。 通常，該方法使用離線數據校準模型參數， 而模型參數易受到荷電狀態 （State of Charge，SOC）和SOH的影響，使得模型精度偏低。為實現參數的動態校準，研究人員提出了遞歸最小二乘法［4］和卡爾曼濾波法（Kalman Filter，KF）［5］，并對算法進行了改進［6］。參數辨識后，可以使用已辨識的參數來估計模型狀態。 ZHOU D等提出高斯過程回歸與擴展卡爾曼濾波（Extended Kalman Filter，EKF）相結合的研究思路［7］，并在電動汽車充電數據上取得了較好的SOH估計結果。 付曉光使用雙卡爾曼濾波結合自定義工況數據實現了電池的SOC估計［8］，算法簡單，易于實現。

筆者以戴維南等效電路模型為研究對象，對雙卡爾曼濾波（Dual Kalman Filter，DKF）算法進行改進，提出一種多時間尺度雙擴展卡爾曼濾波（Multi-time Scale Dual Extended Kalman Filter，MDEKF）算法，并通過應用對比，驗證所提改進算法的有效性。

1 儲能電池運行工況及戴維南模型

1.1 儲能電池運行工況

與電動車輛、電動工具及手機等設備用電池運行工況不同，UPS儲能電池作為電力系統的應急電源，大部分時間浮充運行，由市電向負荷側供電。 在市電異常的情況下，電池放電承擔重要設備的應急電力供應任務。 電池SOH與電壓等參數不同，不能直接使用工具簡單測量得到，而且常規的內阻、溫度、電壓及電流等參數也不足以表征電池SOH。

DL/T 724—2000《電力系統用電池直流電源裝置運行與維護技術規程》［9］要求投入運行的電池組，應定期組織全容量核對性放電試驗， 并及時更換SOH低于80%的電池。 筆者將利用放電深度為50%的恒流放電數據， 實現對儲能電池SOH的精準估計，用電池最大可用容量來表征SOH。

1.2 戴維南模型

戴維南模型在歐姆內阻的基礎上，考慮了電化學極化的影響，可以準確地模擬出電池在恒流條件下的充放電暫態響應曲線。 模型結構相對簡單，計算時間短，在電池的實驗研究中應用廣泛，其結構如圖1所示。

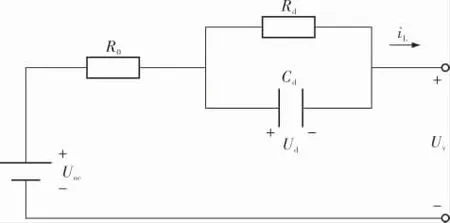
圖1 戴維南等效電路模型

圖1中，Uoc、Uv、Ud分別表示電池的開路電壓OCV、端電壓和極化電壓；R0、Rd、Cd分別表示電池的歐姆內阻、極化內阻和極化電容；iL表示電池的負載電流，圖中箭頭方向表示電流的正方向。 由基爾霍夫定律和安時積分法得到如下公式：

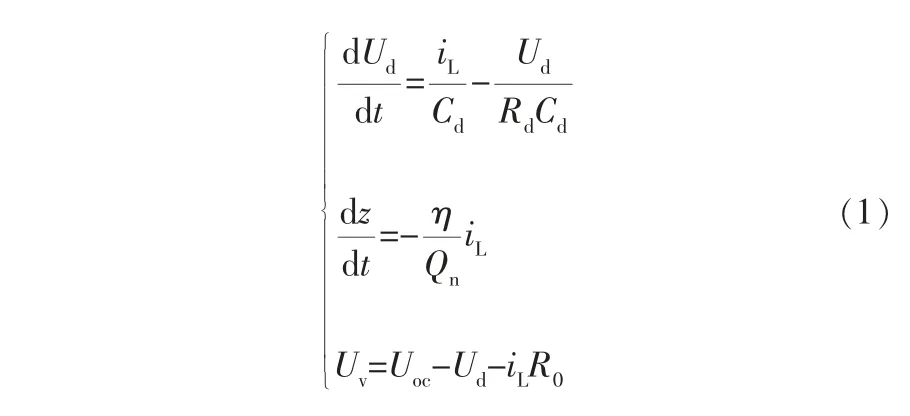
其中，z為電池SOC；η為電池當前充放電倍率下的效率，在0.1C放電倍率下，取值為1；Uoc隨電池z的變化而變化，可視為z的函數；Qn為電池的當前最大可用容量，即SOH的容量表示。

模型離散化。 在單位采樣時間內，電池的參數視為固定值，將模型看作時變定常系統進行簡化，得到下式：

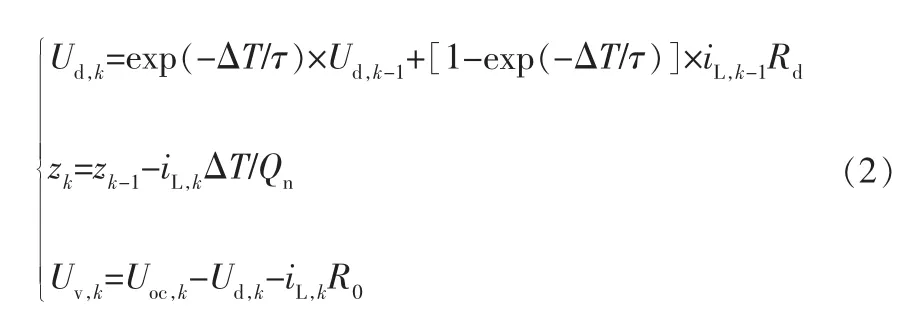
其中， 下標k為時刻；ΔT為采樣時間；τ=RddCdd為時間常數。

不同單體電池的OCV-SOC關系基本相似，通過離線數據進行多項式擬合，得到下式：

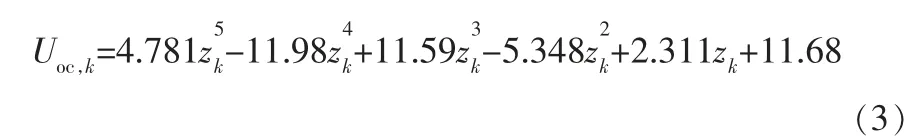
2 儲能電池SOH估計算法的實現

2.1 DKF算法

在DKF算法中， 用KF算法辨識模型參數，從而實現對戴維南模型中歐姆內阻、極化內阻和極化電容的更新； 用EKF算法估計模型狀態， 根據OCV-SOC曲線不斷標定開路電壓，從而實現對戴維南模型中電壓源的更新；然后利用安時積分法逆過程，實現SOH估計。

DKF算法原理如圖2所示。

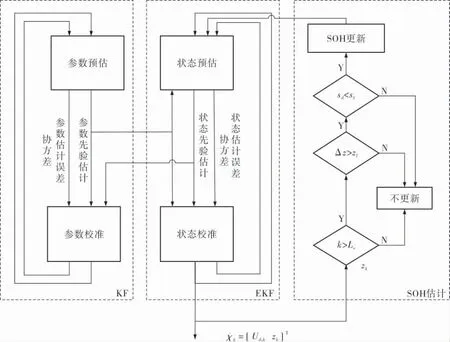
圖2 DKF算法原理示意圖

2.1.1 基于KF的模型參數辨識

將開路電壓Uoc和端電壓Uv的差值記為Uc，由式（2）可得：

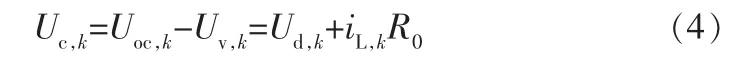
綜合式（2）和式（4），得到下式：

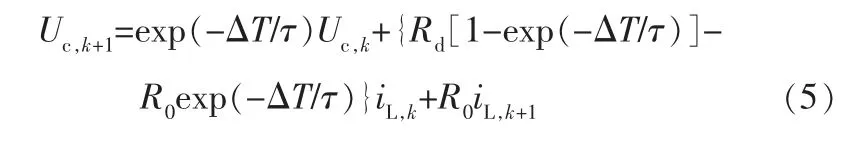
式（5）可以表達為：

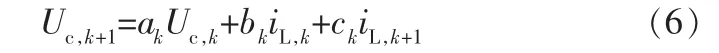
將k時刻的模型參數記為θc，k，得到：

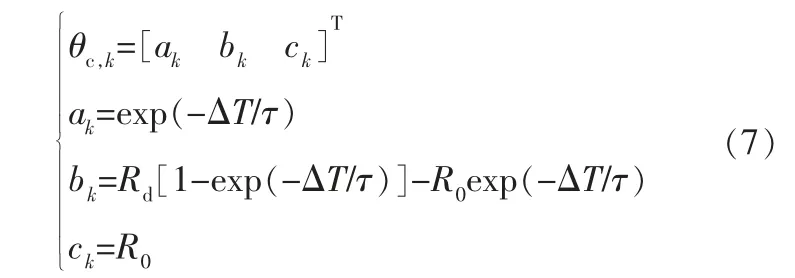
電池的模型參數變化緩慢，在采樣時間內可認為參數保持不變。 將式（6）代入KF算法表達式中，容易得到下式：

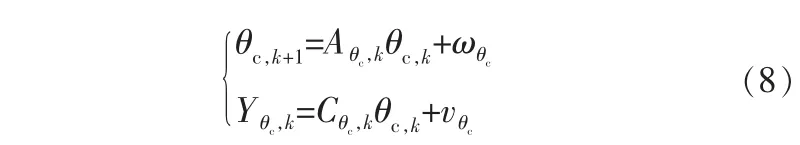
其中，ωθc、vθc分別為參數噪聲和觀測噪聲，協方差矩陣記為Qθc、Rθc。參數向量θc，k、輸出向量Yθc，k、系統矩陣Aθc，k、Cθc，k如下：

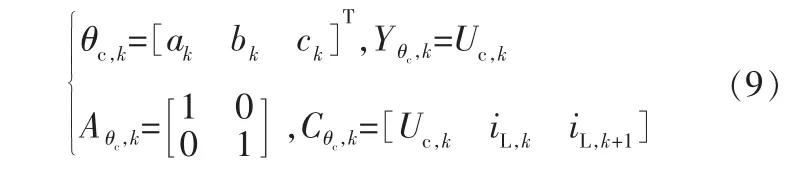
2.1.2 基于EKF的模型狀態估計

將離散化后的電池模型代入EKF算法表達式中，容易得到下式：

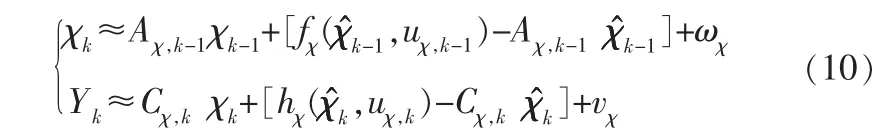
其中，ωχ和vχ為系統的狀態和觀測噪聲，協方差矩陣記為Qχ、Rχ，狀態向量χk的估計值記為χ^k。 輸入向量uχ，k、狀態向量χk、輸出向量Yk、系統矩陣Aχ，k-1、Cχ，k以及狀態方程函數fχ（，uχ，k-1）、觀測方程函數hχ（，uχ，k）如下：

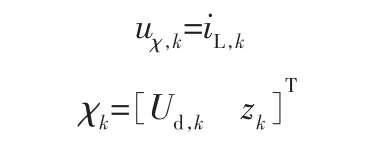
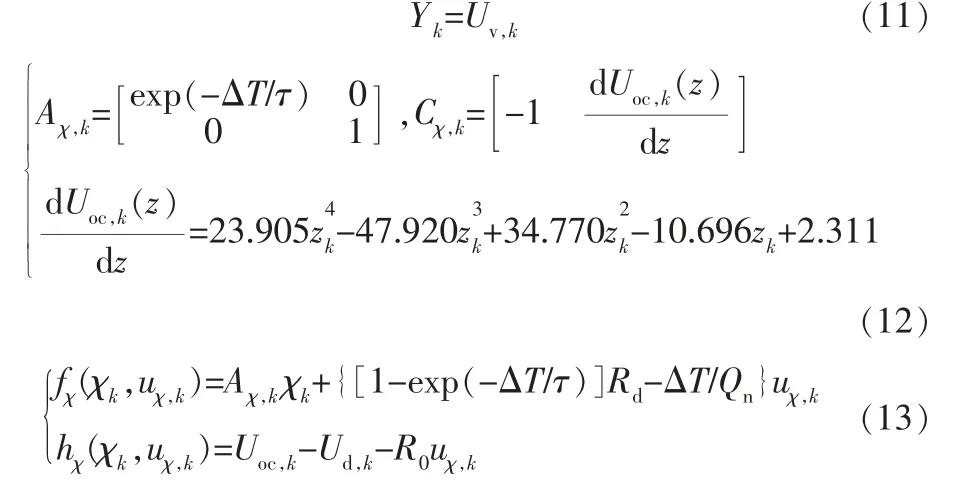
2.1.3 基于狀態估計的SOH估計

電池SOH對OCV-SOC曲線的影響較小， 根據安時積分法逆過程可得到在k時刻算法估計的電池最大可用容量Qn,k：

其中，Ts為SOH更新的時間間隔；Δzk為SOC的變化量；ΔQk為電池容量的變化量。 當Δzk較小時，SOC的估計誤差將嚴重影響SOH的估計精度，因此需要預設約束條件來保障算法的精度和穩定性：

a. 設置時間長度閾值Ls。 應預留充足的算法準備時間，使得SOC估計值能夠精準跟蹤真實值。

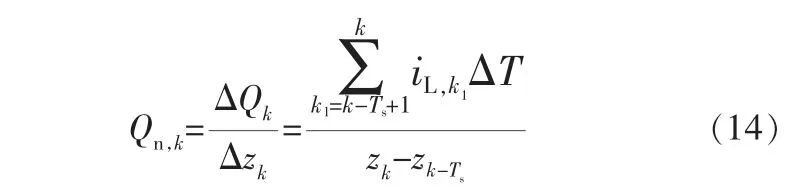
b. 設置Δzk的閾值zf。 當SOC的變化量Δzk大于閾值zf時，才允許更新SOH。 因為Δzk過小的話，容易造成SOH估計波動較大。

c. 設置SOH變化率限制。 應設置SOH變化率閾值sf，防止SOH大范圍波動導致估計結果發散。記SOH的變化率為sd，則有：

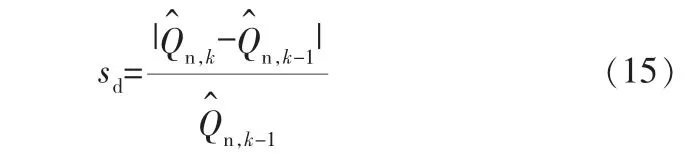
2.2 雙卡爾曼濾波改進算法

2.2.1 雙擴展卡爾曼濾波算法

為增強DKF算法的魯棒性， 筆者對其結構進行改進，調整參數濾波器的新息矩陣與狀態濾波器保持一致，建立起參數辨識和狀態估計的耦合結構。 參數記為θk=［R0RdCd］，代入EKF算法表達式中，容易得到下式：

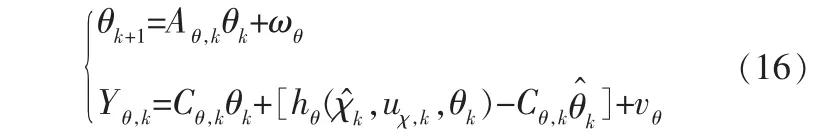
其中，θk為系統參數向量，θk的估計值記為；Aθ，k、Cθ，k為系統矩陣；ωθ、vθ分別為參數和觀測方程噪聲。 各參數向量、輸出向量、系統矩陣以及系統參數方程函數、觀測方程函數如下：

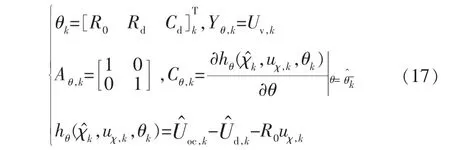
其中，Uoc，k的估計值記為，Ud，k的估計值記為。 需要指出的是，由于參數濾波器觀測方程的新息矩陣與狀態濾波器是一致的，hθ（，uχ，k，θk）的表達式與狀態濾波器的觀測方程hχ（χk，uχ，k）是一致的。

將基于EKF的狀態估計方法與基于EKF的參數辨識方法結合在一起，得到一種雙擴展卡爾曼濾波（Dual Extended Kalman Filter，DEKF）算法。在DEKF算法中，為了統一表達，使用H（χk，uχ，k，θk）表示包含了狀態和參數變量的觀測方程，F（χk，uχ，k，θk）表示包含了狀態和參數變量的狀態方程。

式（17）中，Cθ，k的計算式如下：

式（19）中，通常認為卡爾曼增益矩陣Lχ，k-1與θ是相互獨立的或者說二者之間的關聯性對算法的表現貢獻很小［10］，得到下式：

綜合式（22），初始值設置為0，通過遞推公式得出Cθ，k。

2.2.2 MDEKF算法

結合模型狀態和參數的時變特點，引入多時間尺度對狀態和參數分別在宏觀和微觀尺度上進行估計，得到一種MDEKF算法。

初始化：

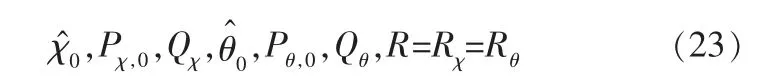
宏觀尺度上，計算參數的時間更新，得到k時刻參數的先驗估計及其估計誤差協方差矩陣

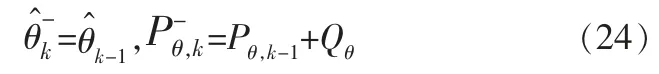
宏觀尺度的時刻記為k， 微觀尺度的時刻記為l， 取值范圍為［1，Lz］，Lz為多時間尺度轉換限值；ln為當前時刻，在數值上等于（k-1）×Lz+l。在微觀尺度上，計算狀態的時間更新，得到ln時刻狀態的先驗估計及其估計誤差協方差矩陣：

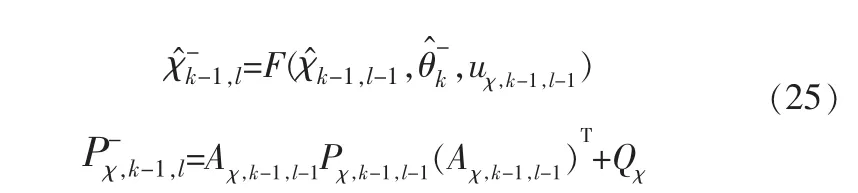
微觀尺度上，計算狀態的測量更新，得到ln時刻的新息矩陣ek-1，l、卡爾曼增益Lχ，k-1，l和狀態的后驗估計及其誤差協方差矩陣Pχ，k-1，l：

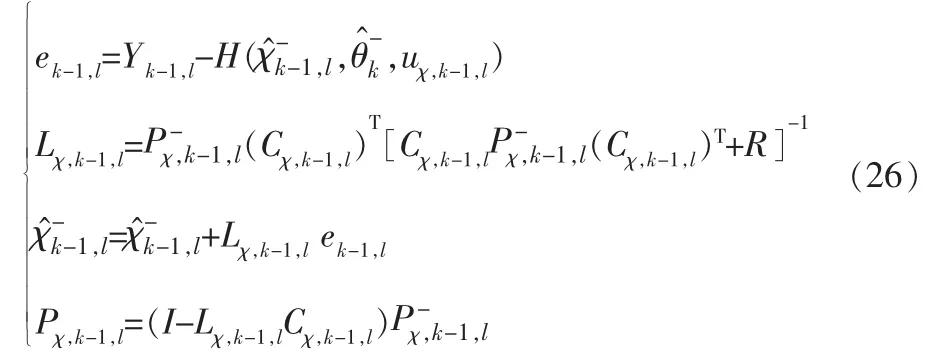
其中，I為單位矩陣。

循環計算，l取值Lz時，完成尺度轉換：

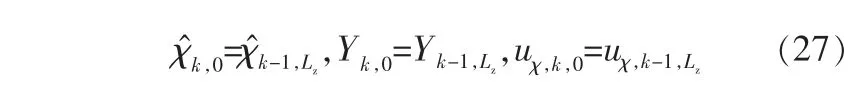
宏觀尺度上，計算參數的測量更新，得到k時刻的新息矩陣ek，0、 卡爾曼增益Lθ，k和狀態的后驗估計及其誤差協方差矩陣：

時間循環更新， 基于SOC的估計值實現SOH估計。

按下式賦值，推移至下一時刻繼續執行上述算法：

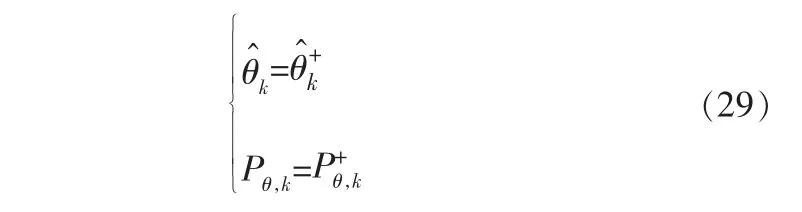
若當前時刻滿足預設的約束條件， 則計算SOH的更新。

MDEKF算法的結構如圖3所示， 圖中Lz為多時間尺度轉換限值，ln為當前時刻。

圖3 MDEKF算法的原理

3 應用算例

筆者選用的電池額定容量為200 Ah， 當前SOH為150 Ah。 在放電深度為50%的恒流放電數據上， 對比DKF、DEKF和MDEKF算法的應用表現，驗證參數辨識和狀態估計的耦合結構以及多時間尺度方法對算法魯棒性和精度的影響。

3.1 算法初始化

在狀態濾波器的初始值設置中， 如果Qχ設置得過小，算法將過于依賴模型，相當于安時積分法，很難收斂，魯棒性弱；如果Rχ設置得過小，算法將過于依賴測量值，相當于開路電壓法，精度很低。 狀態濾波器中的Qχ、Rχ、Pχ，0設置如下：

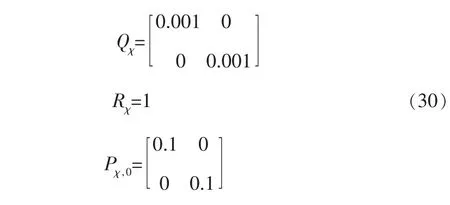
在參數濾波器的初始值設置中，如果Qθc設置得過小，算法將不會更新電池模型參數，導致參數濾波失敗；如果Rθc設置得過小，算法將大范圍更新電池參數，容易導致算法發散。 參數濾波器中的Qθc、Rθc、Pθc，0設置如下：

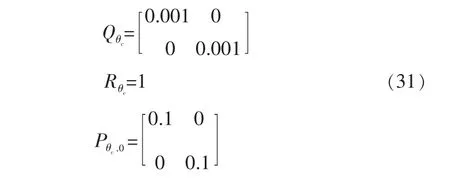
采樣周期ΔT取1 s； 時間長度閾值Ls取2 000 s；Δzk的閾值zf取0. 5%；SOH的變化率閾值sf取0.03。

MDEKF算法多時間尺度轉換限值Lz取60 s；DEKF、MDEKF算法其他參數設置與DKF算法保持一致。

3.2 DKF算法應用

DKF算法在放電數據上的應用表現如圖4、5所示。 圖4a、b分別為歐姆內阻初始值擾動前、后DKF算法的SOC估計和SOC估計誤差對比曲線。圖5a、b分別為歐姆內阻初始值擾動前、 后DKF算法的SOH估計和SOH估計誤差對比曲線。

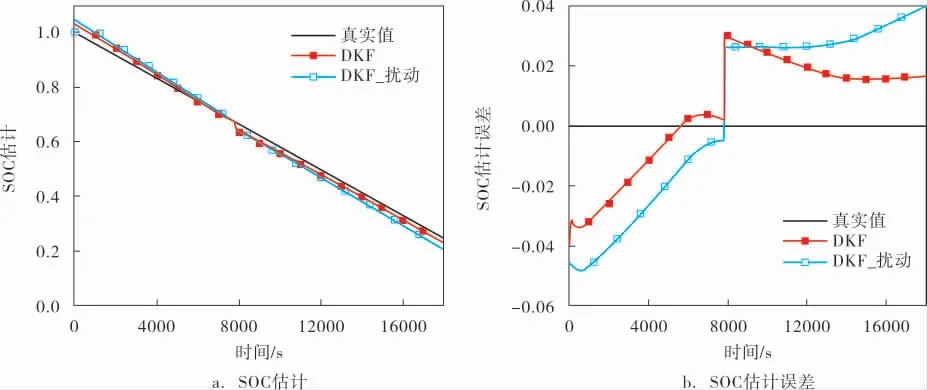
圖4 擾動前、后DKF算法在SOC上的跟蹤效果

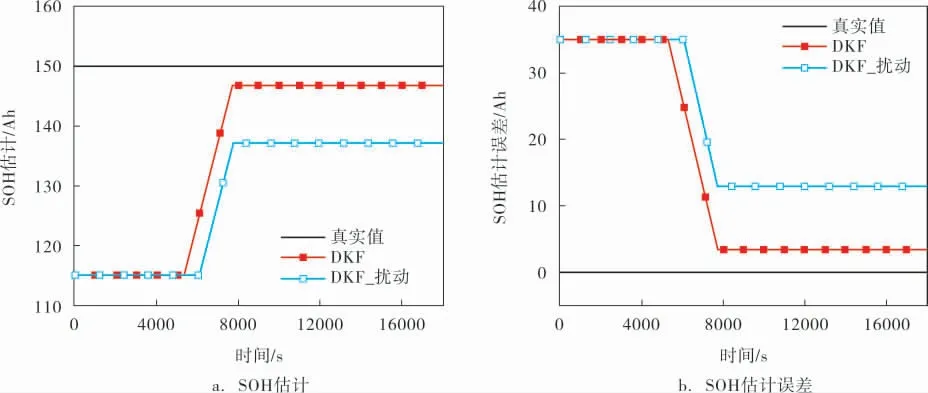
圖5 擾動前、后DKF算法在SOH上的跟蹤效果

綜合圖4、5可以發現： 選擇合適的初始值，DKF算法有著很好的估計精度。 SOC估計誤差最大值控制在0.05以內； 穩定后的SOH估計誤差控制在5 Ah以內；但DKF算法的魯棒性較弱，當模型參數初始值發生擾動后，SOC估計精度降低明顯，穩定后的SOH估計誤差超過了10 Ah。

3.3 DEKF算法應用

DEKF算法在放電數據上的應用表現如圖6、7所示。 圖6a、b分別為歐姆內阻初始值擾動前、后DEKF算法的SOC估計和SOC估計誤差對比曲線。圖7a、b分別為歐姆內阻初始值擾動前、 后DEKF算法的SOH估計和SOH估計誤差對比曲線。

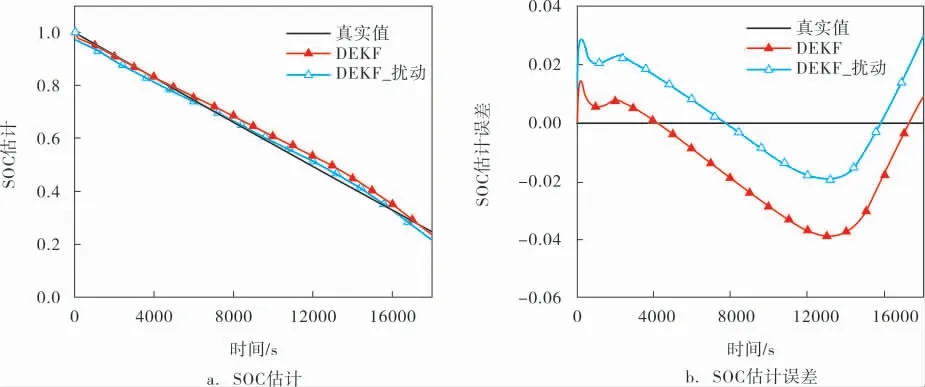
圖6 擾動前、后DEKF算法在SOC上的跟蹤效果

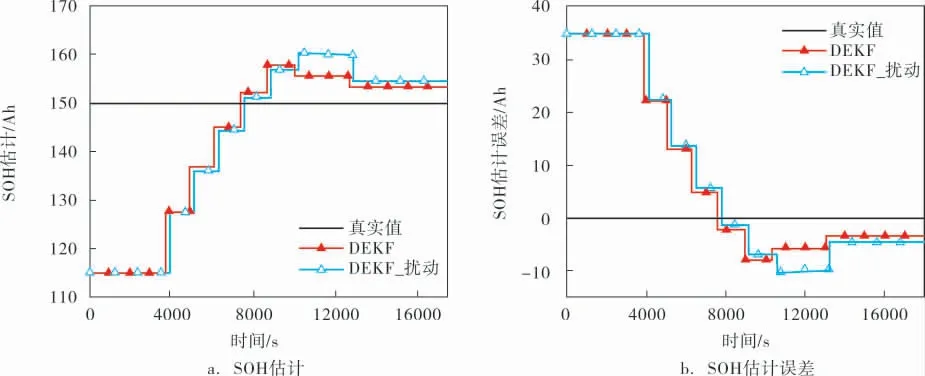
圖7 擾動前、后DEKF算法在SOH上的跟蹤效果

綜合圖6、7可以發現：DEKF算法的魯棒性明顯強于DKF算法， 證實了改進算法的有效性。 擾動前、 后，SOC和SOH的估計精度基本沒有變化，SOC估計誤差最大值控制在0.05以內； 穩定后的SOH估計誤差控制在5 Ah以內。

3.4 MDEKF與DKF、DEKF算法應用對比

MDEKF算法在放電數據上的應用表現如圖8、9所示。 圖8a、b分別為3種算法下的SOC估計和SOC估計誤差對比曲線。圖9a、b分別為3種算法下的SOH估計和SOH估計誤差對比曲線。

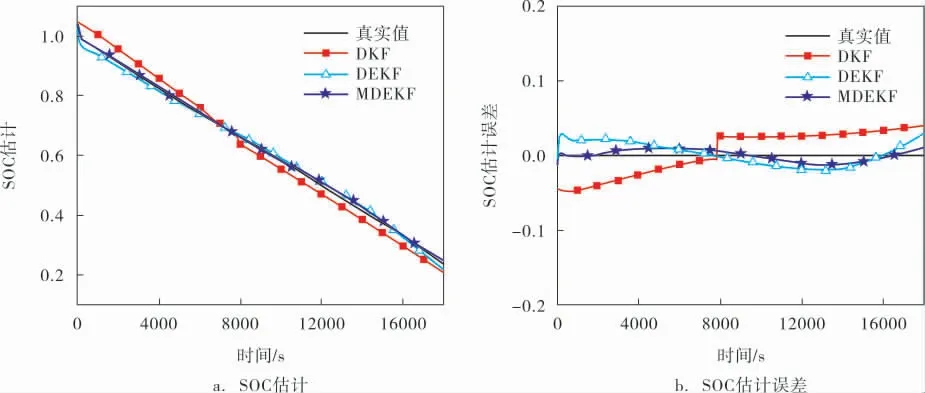
圖8 3種算法在SOC上的跟蹤效果對比

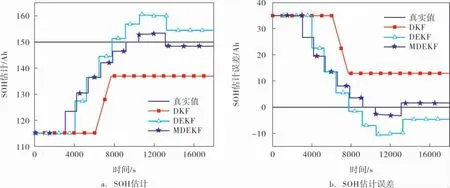
圖9 3種算法在SOH上的跟蹤效果對比

為了更直觀地展示DKF、DEKF和MDEKF算法的估計表現，對應用結果進行統計分析，結果見表1。 其中，平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE） 表征模型的估計精度，MAPE越大，代表樣本的估計誤差越大，估計精度越差。

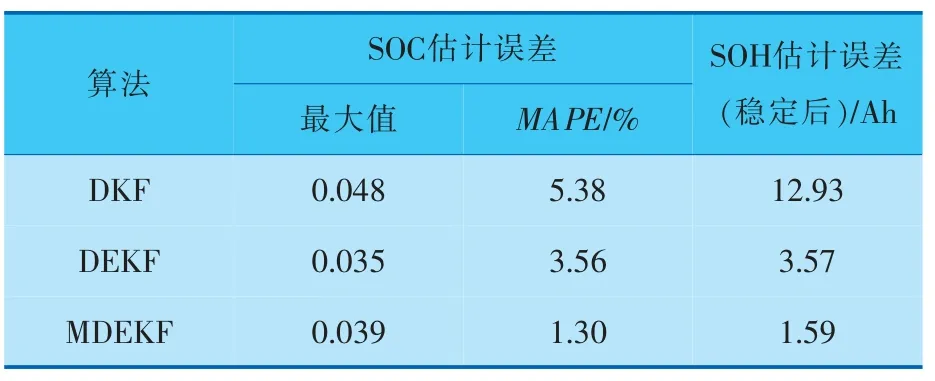
表1 3種濾波算法的實驗結果統計分析

結合應用案例可知：多時間尺度的引入有效地提升了算法的估計精度，證實了所提方法的有效性。 MDEKF算法獲得最佳的估計精度， 其中SOC估計誤差最大值為0.039，MAPE為1.30%；穩定后的SOH估計誤差為1.59 Ah， 誤差百分比為1.06%。

4 結束語

對雙卡爾曼濾波算法進行改進，并結合戴維南等效電路模型，提出基于多時間尺度雙擴展卡爾曼濾波的SOH估計算法。 在儲能電池放電深度為50%的恒流放電數據上的應用結果表明： 參數辨識和狀態估計的耦合結構以及多時間尺度方法的應用，能夠有效地提升算法的估計精度和魯棒性，SOC估計的MAPE小于1.5%， 穩定后SOH估計誤差小于2 Ah。筆者所提出的SOH估計方法，大幅縮短了電池放電的時長和深度，并取得較高的估計精度， 為儲能電池的SOH監測提供了很好的應用模型和算法。