基于改進GRNN的電離層VTEC誤差模型

簡益梅，許承東，王倚文，彭雅奇

(1. 北京理工大學宇航學院，北京 100081；2. 北京空間飛行器總體設計部，北京 100094；3. 中國直升機設計研究所天津直升機研發中心，天津 300000)

1 引言

電離層延遲是衛星導航定位的重要誤差源之一，在GPS測量中，天頂方向的電離層延遲誤差可達2～10m，而在接近地平方向產生的測量誤差甚至可以達到150m。發生電離層延遲的主要原因是導航電磁波穿過電離層時電磁波發生折射，使電磁波傳播方向和傳播速度發生改變，相對真空傳播，產生的電離層折射誤差。

國內外學者對改正電離層延遲進行了大量的研究，目前改正電離層延遲的模型主要有經驗模型、雙頻改正模型和實測數據模型三大類。其中，Klobuchar模型屬于經驗模型中應用比較廣泛的一類模型。經過多年觀測驗證，它的有效性和實用性得到了認可，是一種被廣泛采用的電離層延遲改正模型。Klobuchar模型基本上反映了電離層的變化特性，但其不足之處是改正精度僅能達到50%至60%，已不能滿足日益增長的精度需求。

為提高模型改正精度，大量學者對此進行了研究。文獻[7]在不增加參數的前提下，通過改善夜間項和余弦項的振幅，建立了極地地區單頻全球導航衛星系統(Global Navigation Satellite System，GNSS)用戶的修正Klobuchar模型；文獻[8]在對各種適用范圍較廣的模型精化方案進行歸納的基礎上，提出了一種適用于不同尺度區域的 Klobuchar-like模型；文獻[9]通過采用最小二乘擬合對初始相位和振幅進行改正，建立了適用于小區域的Klobuchar電離層延遲改正模型。

國內外大部分的研究成果從各個方面對 Klobuchar模型進行改進，雖較原模型精度有所提高，但仍存在著對電離層整體改正率不高，模型適用范圍有限等缺陷。在對Klobuchar模型電離層總電子含量TEC(Total Electron Content)研究時，通過與國際GNSS監測評估系統(International GNSS Monitoring & Assessment System，iGMAS)的電離層產品對比，發現Klobuchar 模型預報TEC值的誤差中存在一些周期性的規律現象。廣義回歸神經網絡(GRNN)在時間和空間上有較強的預測能力，文獻[11]提出了一種基于GRNN的電離層電子總含量的建模方法，并結合算例分析初步驗證了該方法的可行性和有效性，但存在精度不高，模型性能表現不穩定等問題。不同于文獻[10]，本文將用GRNN建立TEC的誤差預報模型，但試驗時發現針對短期預報利用的數據樣本不夠豐富，因此，提出一種基于最小二乘法原理的K-折交叉驗證方法以尋找GRNN中的最優徑向學習速度參數，不同的徑向學習速度自適應不同經緯度地區，得到解算誤差并補償到Klobuchar模型，以提高電離層延遲的改正精度。

2 Klobuchar模型誤差分析

2.1 總電子含量(TEC)

沿路徑長度的電子密度稱為總電子含量，其定義為

(1)

TEC以電子/平方米為單位或以TEC單位(TECU)來表示，這里的1 TECU定義為10電子/平方米。天頂方向總電子含量叫做VTEC(Vertical TEC)，TEC與VTEC的關系可通過投影映射函數得到。

圖1 Klobuchar電離層模型VTEC誤差

2.2 經典 Klobuchar 電離層模型

Klobuchar電離層模型是根據中緯度地區大量的實驗資料擬合得到，其夜間電離層天頂時延設為常量5ns(VTEC值為9.23 TECU)，在白天可用本地時余弦函數來近似表示，將每天電離層的最大影響確定為當地時間14：00，基本上能夠反映電離層的變化特性，從大尺度上保證電離層預報的可靠性。GPS采用8參數Klobuchar模型基于地磁坐標系，用Klobuchar模型的8個參數和穿刺點的地磁緯度進行計算，并通過映射函數將天頂電離層延遲投影至傳播方向

(2)

式中為以為單位的垂直方向時延；為以為單位的接收機至衛星連線與電離交點處的地方時；=5×10為夜間的垂直延遲常數；為白天余弦曲線的幅度，由廣播星歷中的系數求得，具體有

(3)

圖2給出了不同緯度下單點的10天內電離層VTEC變化，從圖中可以看出在不同緯度條件下電離層VTEC變化有差異，低緯度區域擬合效果最好，中緯度區域和高緯度區域擬合效果較差，Klobuchar模型的預報精度也不夠精確。

初始相位對應余弦曲線極點的地方時，一般取為50400，為余弦曲線的周期，根據廣播星歷中系數求得。其中

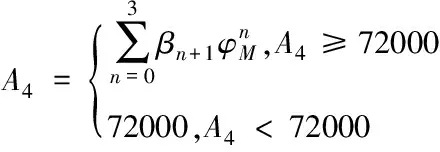
(4)

式中為電離層穿刺點的地磁緯度。

通過Klobuchar模型可求得天頂電離層時延，利用式(4)即可得到廣播星歷預報的VTEC

(5)

其中為光速，為測量時延時相應的頻率。

2.3 iGMAS 電離層產品

iGMAS導航數據分析中心利用分布在全球的觀測站資料解算電離層TEC分布圖，并從當日UTC0起每隔兩小時生成一張TEC地圖產品，全天共12張，其沿緯度和經度方向的數據點間隔分別為2.5°和5°，最后以IONEX(Ionospheric Map Exchange，IONEX)格式對外發布。iGMAS能夠提供高精度的全球電離層延遲模型事后產品，到無論是時空覆蓋率還是精度都是相當高的水準。因此本文將iGMAS的最終產品作為客觀標準，在此基礎上進行誤差分析。

2.4 誤差分析

圖1給出了GPS L1信號頻率下，2020年2月13日14點的Klobuchar模型VTEC預報誤差。從圖中可以看出Klobuchar模型給出的VTEC與iGMAS的精密VTEC相比之下較粗糙，Klobuchar模型能大致擬合VTEC分布，且在低緯度地區的擬合情況相對較好，但在中緯度地區和高緯度地區存在著不小的誤差。

圖2給出了不同緯度下單點的10天內電離層VTEC變化，從圖中可以看出在不同緯度條件下電離層VTEC變化有差異，低緯度區域擬合效果最好，中緯度區域和高緯度區域擬合效果較差，Klobuchar模型的預報精度也不夠精確。

圖2 不同點處電離層VTEC變化情況

圖3給出了中緯度一點(30°N，90°E)在不同季節下一周內電離層VTEC變化，從圖中可以看出Klobuchar模型能大致擬合其變化趨勢，且由于太陽光照、地球運動等因素，不同季節下的VTEC變化情況也不一樣，夏季擬合效果較好，春、秋和冬季較差。同時，從圖3中也可看出Klobuchar模型與iGMAS精密產品的誤差呈現出了一定的周期性變化規律，尤其秋季和冬季更為明顯。

圖3 不同季節電離層VTEC變化情況

3 改進廣義回歸神經網絡誤差預測模型

3.1 廣義回歸神經網絡

1991年D.F.Specht博士提出廣義回歸神經網絡，它是徑向基網絡的變種。GRNN建立在非參數回歸的基礎上，以樣本數據為后驗條件，執行Parzen非參數估計，依據最大概率原則計算網絡輸出。

GRNN具有很強的非線性映射能力和柔性網絡結構以及高度的容錯性和魯棒性，適用于解決非線性問題。相較于徑向基網絡，GRNN在逼近能力和學習速度上有更強的優勢。

GRNN在有4層結構，如圖4所示，分別為輸入層、模式層、求和層和輸出層。

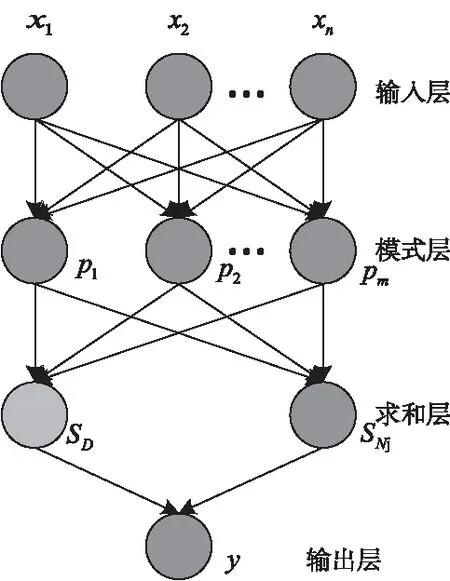
圖4 GRNN結構

1)輸入層

輸入層神經元的數目等于輸入數據向量的維數n，各神經元將輸入向量直接傳遞給下一層神經元。

2)模式層

模式層神經元數目為輸入數據樣本的數目m，每個神經元接收不同的樣本，模式層神經元的傳遞函數為

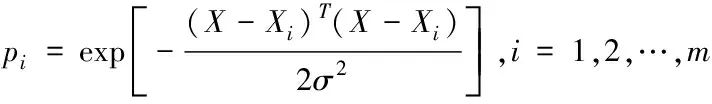
(6)

其中神經元的輸出為輸入數據與其對應的樣本之間的歐氏距離平方的指數平方=(-)(-)的指數形式。式中，為輸入；為第個神經元對應的輸入數據樣本。

3)求和層

求和層包含兩種類型神經元。第一種是對所有上一層神經元的輸出進行算術求和，計算公式為

(7)

與上一層神經元的連接權值均為1，傳遞函數為

(8)

第二種是對所有模式層的神經元進行加權求和，計算公式為

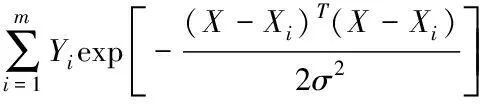
(9)

模式層中第個神經元與求和層中第個分子求和神經元之間的連接權值為第分輸出樣本中的第個元素，傳遞函數為

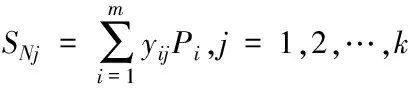
(10)

4)輸出層

(11)

3.2 基于K-折交叉驗證的GRNN電離層VTEC誤差預報模型

GRNN是在徑向基網絡的基礎上改進的，徑向基網絡是由輸入層、隱含層和輸出層構成，隱含層采用的徑向基函數的閾值B能夠影響輸出對輸入的響應靈敏度，但B本身不是訓練GRNN的可見參數，在MATLAB內部，網絡分布密度spread(S)起到了B的作用。根據文獻[15]，B與S的關系為

(12)

通常情況下，S越小，函數的逼近越精確，但逼近過程會不平滑，網絡性能差，可能導致過適應現象；S越大，函數擬合越平滑，但是逼近誤差會變大，需要的隱藏神經元也越多，計算量也越大。因此本文提出利用K-折交叉驗證(K-fold Cross Validation，K-CV)的方法來選取最佳S值。即，將訓練數據分成K組，每個子集數據分別做一次驗證集，其余K-1組子集作為訓練集，以驗證集的最小均方誤差為性能指標，這樣會得到K個模型下的最佳S，取這K個S的平均值作為GRNN電離層VTEC誤差預報模型的最終S。在電離層TEC網格里，每一個點都能自動匹配最適合自身的S值。

具體實施步驟如下：

1)選取網絡輸入輸出，本文將數據時序、穿刺點經度、緯度、周內秒、小時數以及Klobuchar模型計算出來的VTEC作為輸入，故輸入層有6個神經元；將VTEC誤差作為輸出；

2)歸一化處理，不同的參數往往具有不同的量綱，這樣的情況會影響到數據分析，因此需要對數據進行量綱統一；

3)數據分類與交叉驗證，將用到的樣本數據合理分為訓練數據和測試數據，在訓練數據中利用K-CV來尋找最佳S值；

4)將上一步得到的S值與樣本數據訓練GRNN模型得到基于K-折交叉驗證的GRNN電離層VTEC誤差預報模型。

4 試驗與分析

為驗證該模型的有效性和實用性，試驗數據選取從武漢大學IGS數據中心獲取的2020年8月21日起共10天廣播星歷數據，計算出Klobuchar模型與精密電離層產品的VTEC誤差。考慮到電離層VTEC每隔兩小時播報1次，為體現預報效果，將前7天的數據用于訓練GRNN模型，故K-CV中的K值選為7，后3天的數據作為測試數據來評價該模型的預報效果。本試驗選取包含低、中、高緯度的9個電離層穿刺點作為試驗點，如圖5所示，分別為

P1(0°,120°E)P2(0°,90°E)P3(0°,60°E)P4(30°N,120°E)P5(30°N,90°E)P6(30°N,60°E)P7(60°N,120°E)P8(60°N,90°E)P9(60°N,60°E)

圖5 試驗點選取分布圖

試驗時還加入了未優化S值的原始GRNN模型進行對比，試驗結果如圖6所示。從圖中可以看到，原始GRNN模型對真實誤差的預測效果差，僅能大致擬合變化趨勢，在數值上存在較大差異，而改進后的GRNN模型在不同緯度的表現均優于原始GRNN模型，能較好擬合Klobuchar模型電離層VTEC值誤差，且得益于優化的S值，在不同緯度表現均很穩定。

為進一步說明改進后GRNN模型的預測效果，表1中計算了該模型在不同穿刺點下的預測值的絕對值的均值偏差，并與原始GRNN模型進行比較。原始GRNN模型能夠大致擬合Klobuchar模型中電離層VTEC值誤差，但精度不高，誤差補償精度平均為47.7%，同時原始GRNN模型表現也不穩定，在9個試驗點中，誤差補償精度最高達到80%，最差低至2%。而改進后的GRMM模型則表現得更穩定，誤差補償精度平均為62.4%，且能夠在原始GRNN模型的基礎上將再提升5%-30%，對Klobuchar模型的誤差補償精度為32%-89%。

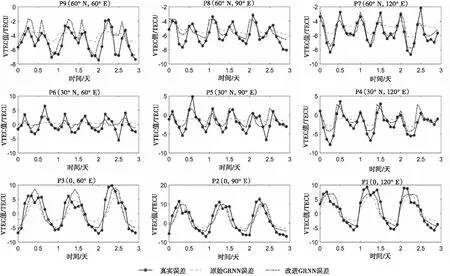
圖6 9個試驗點的模型預測情況

表1 不同模型補償精度提升情況

為更進一步說明模型的有效性，圖7給出了中緯度一點(30°N，90°E)在不同季節下10天(2019年12月21日至30日；2020年3月20日至29日；2020年6月21日至30日；2020年8月21日至30日)的電離層VTEC誤差值預測情況，不同季節下各選10天的數據，前7天用來訓練，后3天用來預測，同樣也與原始GRNN模型進行對比。

圖7 不同季節模型VTEC預測情況

表2給出了對應的預測均值偏差，從表中數據可看出GRNN模型可有效補償Klobuchar模型誤差，且改進后的GRNN模型補償效果更好，誤差補償精度為46%-90%，相對原始GRNN模型提升10%-20%。

表2 不同季節不同模型補償精度對比

事實上，影響電離層VTEC值的因素非常多，除了地理位置和時間之外，太陽活動，宇宙射線等都會對其產生影響。隨著對這些因素的不斷了解深入，將相關因素也作為模型的輸入參數以更進一步提高模型精度是下一步的研究方向。

5 結論

在利用Klobuchar模型計算電離層VTEC值時發現該模型計算得到的VTEC值與iGMAS提供的最終電離層產品中的值之間存在著一些周期性變化的規律，針對這一現象本文提出了一種改進GRNN對該模型VTEC值誤差進行預測和補償。在Klobuchar模型的基礎上，利用改進GRNN模型對不同經緯度穿刺點和不同季節的VTEC誤差進行預測，并與原始GRNN模型進行對比驗證了本文提出優化方法的有效性和實用性。應用改進后的GRNN模型對本文選取的不同試驗點的VTEC誤差進行預測和補償，可減小Klobuchar模型預報誤差的32%-90%，對于減小導航系統級誤差具有重要意義。