基于模糊邏輯系統的采礦船升沉補償控制方法研究

滕媛媛,陳林愷*,孫友剛,謝穎

(1.上海海事大學物流工程學院，上海 201306；2.同濟大學鐵道與城市軌道交通研究院，上海 201306；3.上海振華重工(集團)股份有限公司，上海 201306)

深海采礦船在海面上運行的時候由于海浪的涌動會作升沉運動，從而嚴重影響船體和采礦系統的安全。為保證深海采礦船在進行作業的時候可以安全運行，所以需要對其進行升沉補償。由于在當前升沉補償系統一般可以分為被動式、主動式，前者結構簡單、補償精度差，后者結構復雜、耗能高、補償精度好。周強等[1]通過在絞車型升沉補償模擬試驗臺上進行研究；展勇等[2]對半主動升沉補償系統進行非線性建模與仿真；袁建新[3]對采用液壓驅動的主動升沉補償模型控制研究，為了更好地模擬真實海浪情況，王玉紅等[4]對升沉補償系統實驗平臺進行設計并展開研究;段玉響[5]對海上吊裝主動式升沉補償與防擺控制系統進行了分析和研究,但是這些學者對于升沉補償系統的研究大部分是在機械方面的革新，很少有從控制算法的角度進行。控制算法的改善對于機械也可以起到很好的效果。李帆等[6]對橋式起重機的防搖采取模糊比例積分微分(proportion integral derivative，PID)算法進行研究；仝新峰等[7]利用模糊-內模雙環控制算法對船岸并網系統進行了分析和研究。基于此，首先分析了當前主流升沉補償系統的優缺點，并提出了一種結合二者優點的主被動復合式升沉補償系統，再從控制算法的角度設計模糊控制算法進行控制，最后在Simulink中進行仿真，并將模糊控制算法的仿真結果和傳統PID控制算法的仿真結果比較，以驗證所提系統和算法的有效性。

1 升沉補償系統的結構和工作原理

1.1 升沉補償系統結構

采用的升沉補償系統是主被動復合式該補償系統主要的組成部分包含液壓站、絞車、液壓缸、蓄能器組等，其系統結構簡圖如圖1所示。

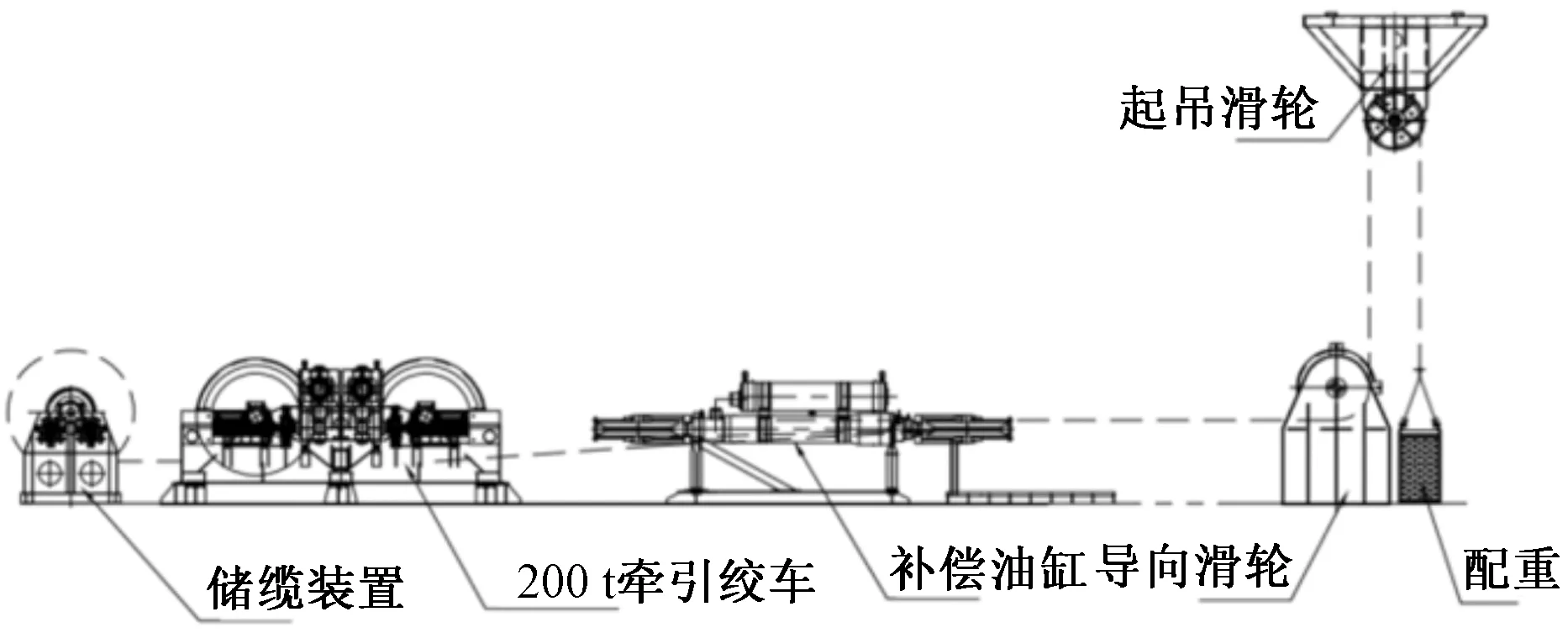
圖1 主被動復合式升沉補償系統結構簡圖Fig.1 Structure diagram of active and passive compound heave compensation system

1.2 升沉補償液壓系統原理

針對被動式補償系統精度不高、主動式補償系統能耗過大的缺點，采用主被動復合式升沉補償系統。在不同工況下可實現被動補償功能與主動補償功能的切換，具備更廣泛的負載適用性。其液壓原理簡圖如圖2所示。

圖2 主被動升沉補償系統液壓原理簡圖Fig.2 Schematic diagram of hydraulic principle of active and passive heave compensation system

被動補償模式下，比例閥、被動腔充液閥關閉，連通閥打開，主動腔A和B連通，被動腔C與被動腔蓄能器連通，通過蓄能器的柔性吸收升沉運動;一般情況下，被動模式和主動模式是同時工作的，但系統主要是在主動模式下工作。此時連通閥、被動腔充液閥關閉，比例閥根據采集的升沉運動信號閉環控制 補償液壓缸運動，可大幅抵消升沉運動。同時被動腔與蓄能器相連平衡重物重量，可以降低主動控制系統的能耗。

2 采礦船升沉幅值的計算

海浪的激勵作用會導致采礦船作升沉、縱搖、進退等六自由度運動，其中升沉運動對采礦船水下系統的安全性影響最大。船舶在海浪作用下升沉方向的動力學響應和船體的重量、外形、尺寸等因素息息相關。船體升沉一般近似為諧波運動，利用采礦船的型號、尺寸、結構及海浪的波長、波高和頻率可計算采礦船升沉運動的周期和幅值等參數。假設采礦船的升沉運動為某一簡諧運動，則其升沉運動函數為

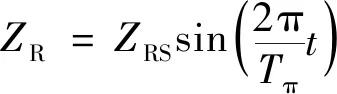
(1)

式(1)中：ZR為采礦船的升沉位移；ZRS為采礦船的升沉幅值；TH為海浪的波動周期；t為采礦船運動的時間。

根據莫爾經驗公式，可以推導出ZRS的計算公式為

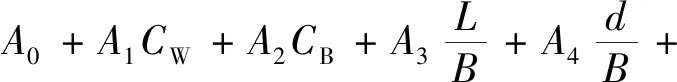
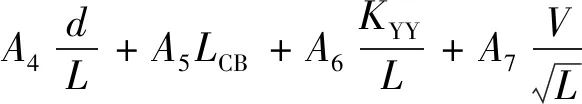
(2)

式(2)中：A0,A1，…，A7為隨風浪大小和傳播尺寸變化的相關系數，需查表2得；CW為水面線系數；CB為方形系數；L為水面線系數；B為船舶寬度；d為船舶的設計吃水深度。

計算采礦船升沉復幅值和周期所需參數如表1所示。

表1 計算采礦船升沉復幅值和周期所需參數Table 1 Parameters required to calculate the recovery amplitude and period of the mining ship heave

A0,A1,…,A7為相關系數，取決于風級和船的體積，其取值如表2所示。

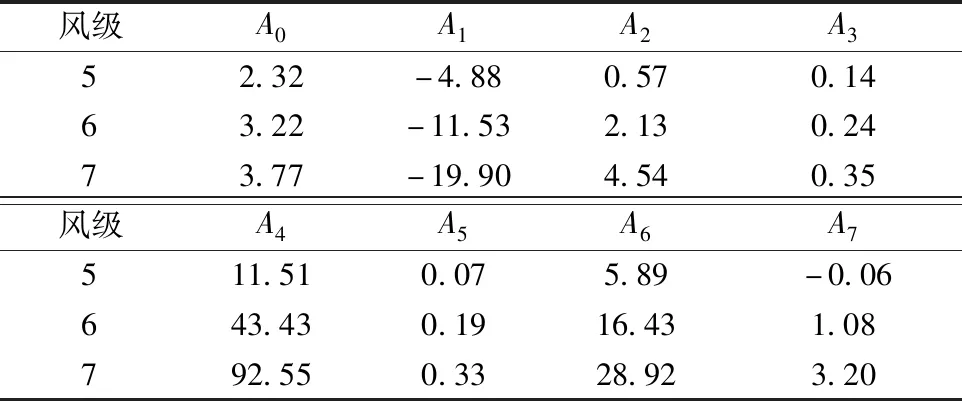
表2 相關系數的插值結果Table 2 Interpolation results of correlation coefficients

經計算，得出在波高為±2.5 m、周期為5.8 s的海況下，采礦船的升沉幅值為0.36 m，周期為5.8 s。

3 升沉補償系統數學模型的建立

升沉補償系統的組成部分包括比例閥、復合液壓缸、活塞式蓄能器等。因此要對其各組成部分的模型進行數學建模，并且推導出中間傳遞函數，最后才可以推導出總傳遞函數。

3.1 比例閥模型

由于比例閥的組成環節比較多，因此很難知道各種參數并建立一個精確的數學模型。在實際應用中，需將閥芯運動簡化為一階系統，其傳遞函數為

(3)

式(3)中：TXU為閥芯運動的時間常數；KXU為閥芯位移-電壓增益系數。

3.2 復合液壓缸模型

沉補償系統采用復合式液壓缸結構，如圖3所示。采用復合式的設計，把主動油缸和被動油缸集成在一起，在實現主動被一體化的同時大大節約了裝備空間。

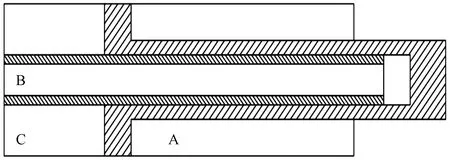
圖3 復合式液壓缸結構示意圖Fig.3 Schematic diagram of compound hydraulic cylinder structure

根據牛頓第二定律，鋼絲繩拉力與重物受力平衡方程為

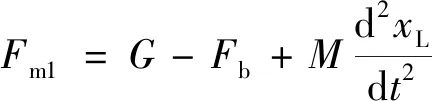
(4)

式(4)中：Fm1為鋼絲繩拉力；G為采礦船重力；Fb為負載浮力；XL為負載位移。

在主動升沉補償作用下，液壓缸受力平衡方程為

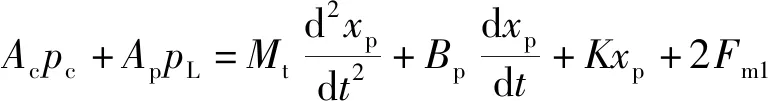
(5)

式(5)中：Ac為液壓缸被動腔C腔作用面積；pc為蓄能器液壓力；Ap為液壓缸主動腔A、B腔的作用面積，Ap=Aa=Ab;pL為系統壓力；Mt為液壓缸缸桿處的等效質量；xp為補償液壓缸位移；Bp為黏性阻尼系數；K為液壓缸缸桿處的等效負載剛度。

液壓缸主動補償腔流量連續性方程為

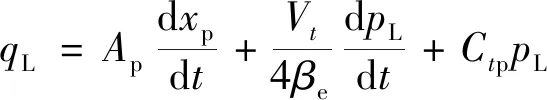
(6)

式(6)中：qL為液壓缸負載流量；Vt為液壓缸作用有效體積；Ctp為液壓缸總泄漏系數；βe為有效體積彈性模量。

3.3 活塞式蓄能器模型

活塞式蓄能器采用浮動活塞將液體與氣體隔離，并和氣瓶組合使用。在大流量、大體積的工況下可以保證液壓油輸出壓力的相對穩定。

活塞式蓄能器活塞受力平衡方程為

式(7)中：pg為氣體壓力；Ag為活塞蓄能器活塞作用面積；m為活塞質量；Bg為等效黏性阻尼系數；Kg為等效剛度系數；xg為活塞蓄能器活塞位移；Ffg為活塞摩擦力。

3.4 半主動模式下主動補償系統模型

液壓缸主動補償腔流量連續性方程為

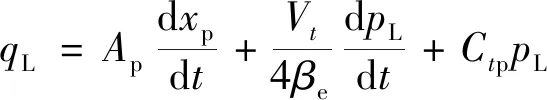
(8)

在升沉補償作用下，液壓缸受力平衡方程為

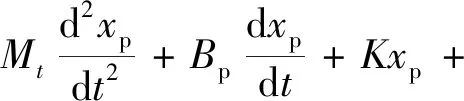
(9)

式(9)中：FZZ為垂直方向上的流體慣性力。

因此，半主動補償模式下,比例閥閥芯位移產生的液壓缸缸桿位移傳遞函數為

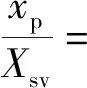
(10)

式(10)中：Kce為總泄露系數；Xsv為比例閥閥芯位移。

4 主動升沉補償控制器設計

在半主動升沉補償模式下，需要針對主動式補償工作模式，設計基于模糊邏輯系統的PID控制器。

模糊邏輯控制方法適用于相對復雜且目前無法得到精確模型的控制系統中，可以提高系統的控精度，故該方法目前使用較為廣泛。針對升沉補償系統的參數不確定性、非線性強、有滯后的特點，用模糊邏輯系統可實現無模型下的控制器設計以提高主動補償系統的魯棒性。模糊邏輯系統的設計過程如圖4所示[8]。

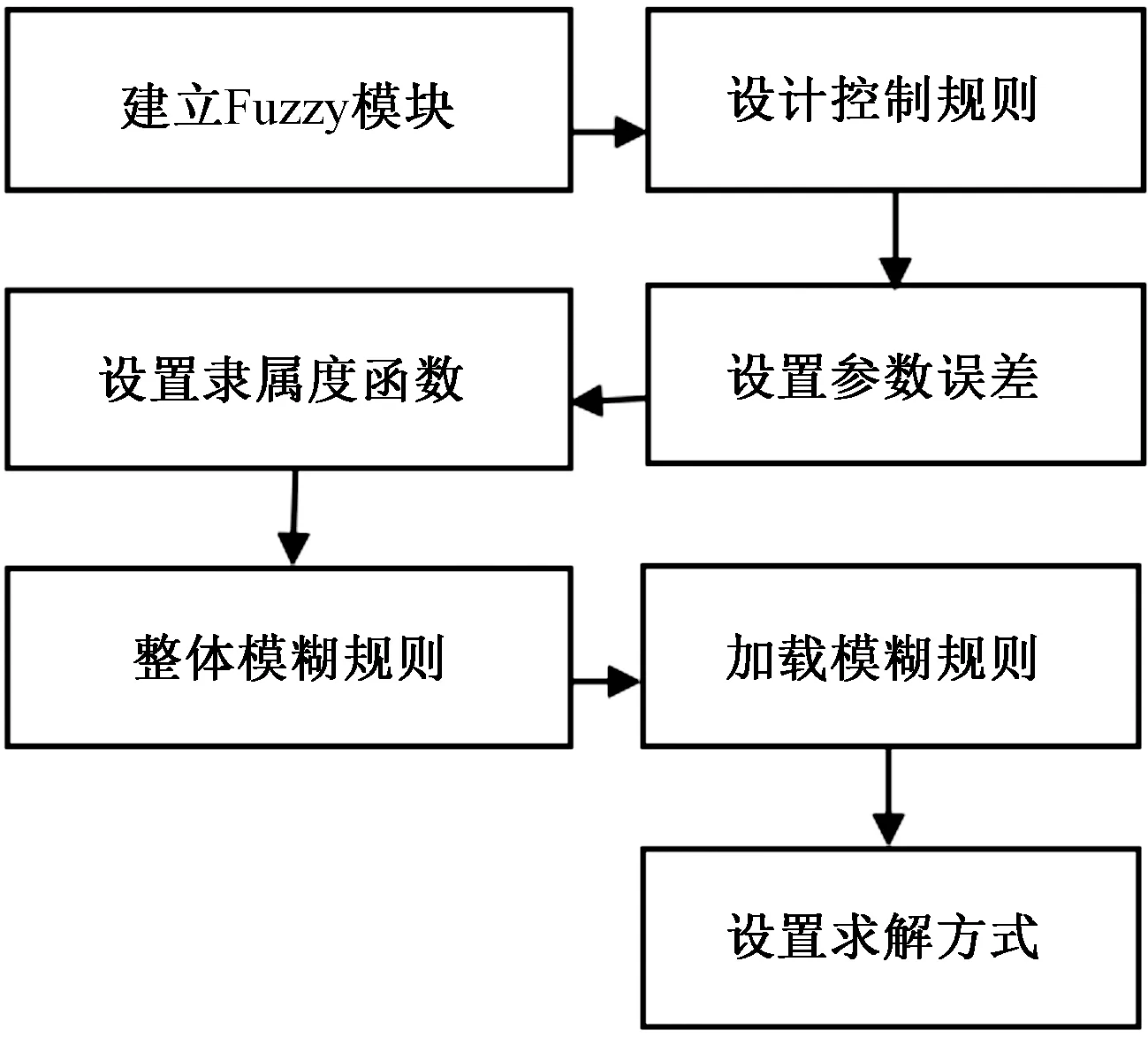
圖4 模糊算法設計的步驟流程圖Fig.4 Flowchart of fuzzy algorithm design

根據采礦船作業特點和控制經驗，所提出的模糊規則如表3所示。建立模糊控制規則其實就是將控制經驗通過模糊語言描述出來[9]。常用的模糊控制器形式有Mamdani型和T-S型。相比于T-S模糊邏輯系統，Mamdani型模糊規則輸出為模糊量，與人類的自然語言信息相似，易于理解，因此選擇Mamdani型控制器[10]。

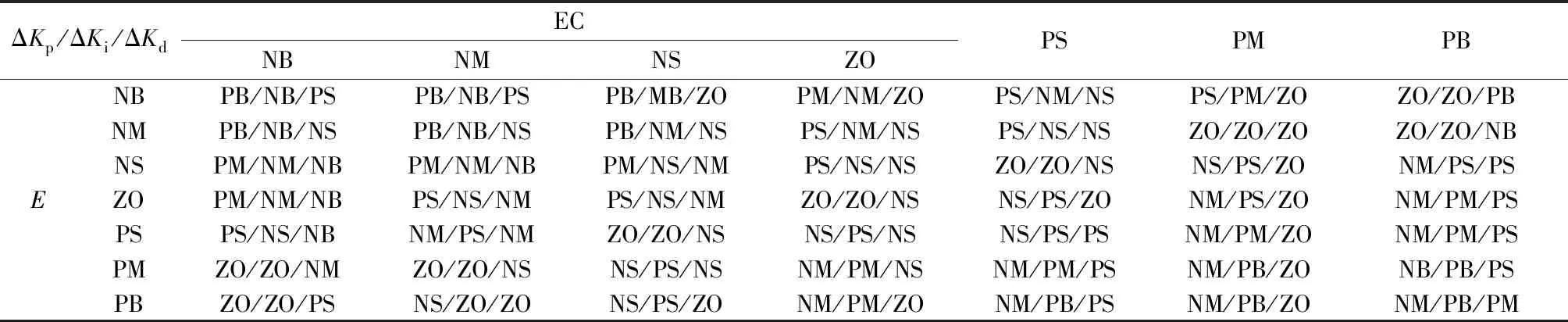
表3 模糊規則Table 3 Fuzzy rules

基于模糊邏輯系統的PID 控制器的設計過程如下：首先定義e為實際位移和期望位移的差值，ec為實際位移和期望位移的差值隨著時間變化的變化率。再通過傳感器對e與ec的變化率 進行檢測，然后通過量化因子Ke與Kec將其轉化到模糊論域中，從而得到要PID控制器3個參數的增量ΔKp、ΔKi、ΔKd[11]。

模糊控制器的一般原理表達式為

(11)

式(11)中：Kp為模糊控制器的比例控制參數；Ki為模糊控制器的積分控制參數；Kd為模糊控制器的微分控制參數。

最后對3個參數進行計算,得到最終輸入PID控制器的參數，可表示為

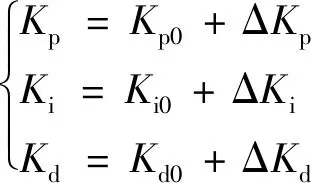
(12)

代入式(9)，得到本升沉補償模糊控制器的設計的最終表達式為

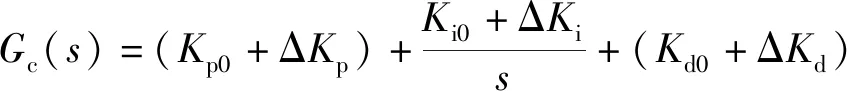
(13)

式(13)中，Kp0為初始時刻的Kp值；ΔKp為Kp值的變化量；Ki0為初始時刻的Ki值；ΔKi為Ki值的變化量；Kd0為初始時刻的Kd值；ΔKd為Kd值的變化量。

結合本升沉補償系統實例，可得到圖5所示的3D可視化模糊規則，更直觀地看出Kp、Ki、Kd隨著e和ec的變化而變化的情況[12]。

圖5 Kp、Ki、Kd的可視化模糊規則示意圖Fig.5 Schematic diagram of visual fuzzy rules for Kp、Ki、Kd

5 仿真結果

模型搭建完需進行仿真，所提升沉補償系統的仿真參數如表4所示[13]。

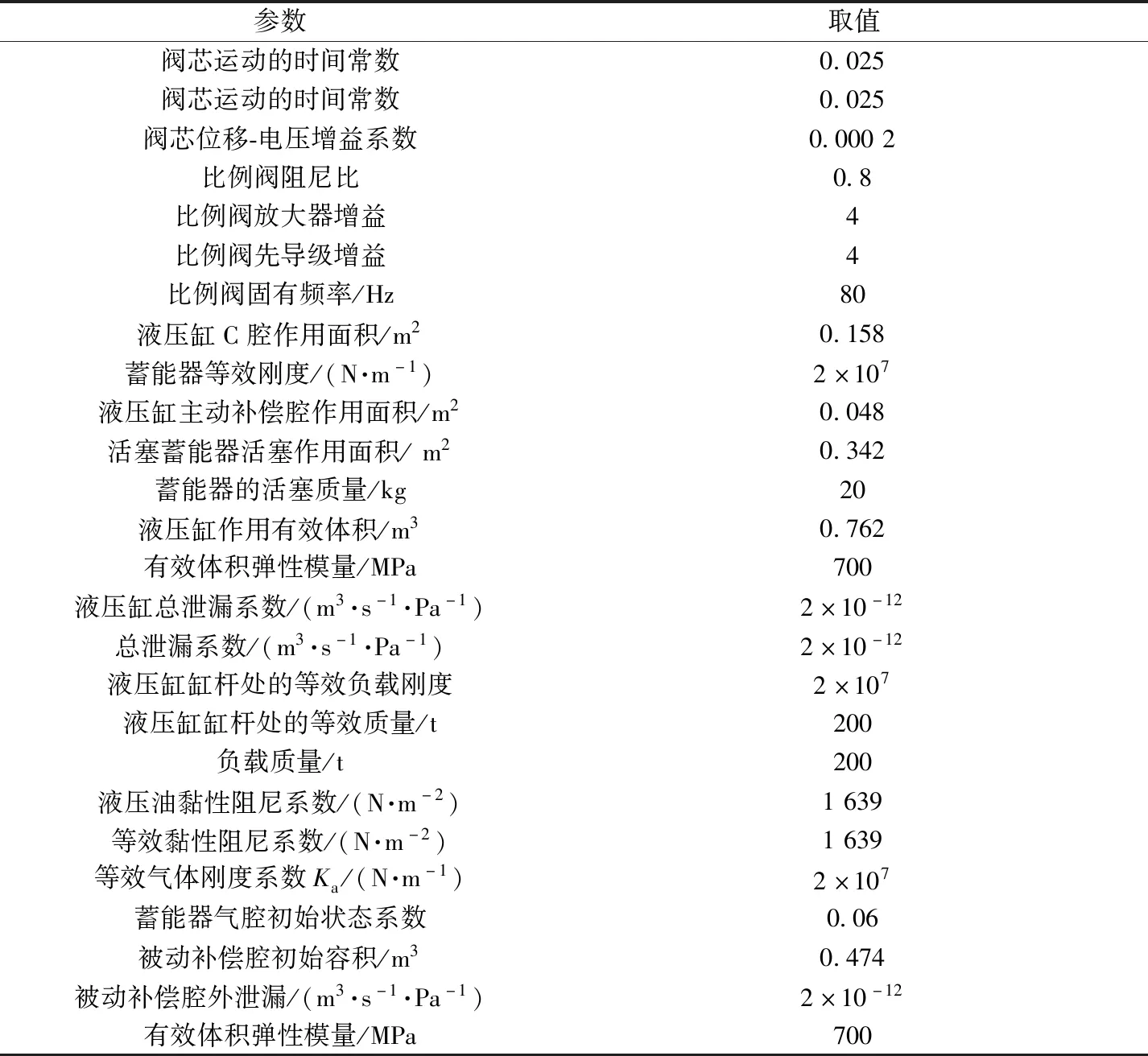
表4 半主動式升沉補償系統仿真參數Table 4 Simulation parameters of semi-active heave compensation system

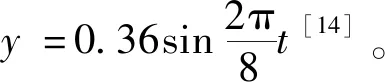
圖6 采礦船的實際升沉位移曲線Fig.6 Actual heave displacement curve of mining ship

在規則海浪波下，利用模糊控制對升沉補償系統對主動補償模式進行控制，模糊控制算法中，先設定一個PID參數的預設值和誤差范圍，PID參數可以實時變化，起到自動調節PID參數的作用[15]。PID參數分別預設為150、50 10，仿真時間為50 s。模糊控制中PID參數變化過程示意圖如圖7所示，其中圖7(a)、圖7(b)為規則海浪波下PID參數變化，圖7(c)為不規則海浪波下PID參數變化[16]。二者的仿真結果曲線示意圖如圖8所示。

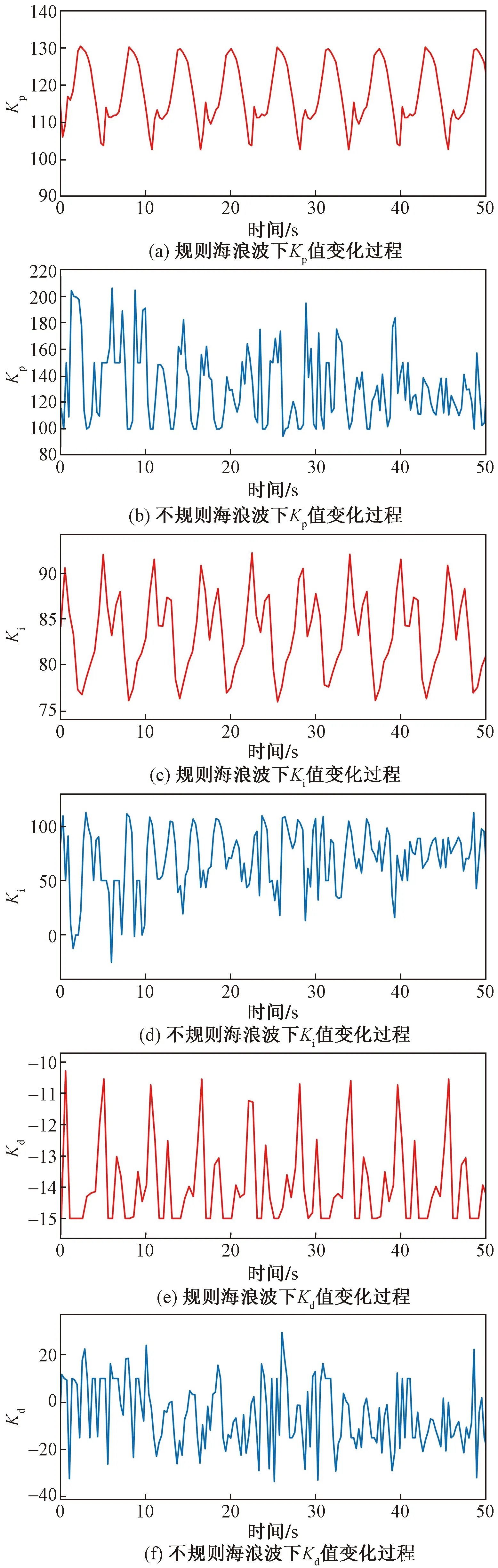
圖7 模糊控制算法下Kp、Ki、Kd值變化過程Fig.7 Value change diagram fuzzy control algorithm forKp，Ki，Kd

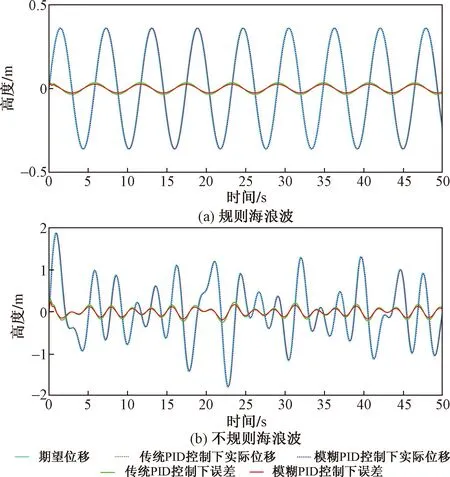
圖8 模糊控制和傳統PID控制算法下仿真結果對比Fig.8 Comparison of simulation curves between fuzzy control and traditional PID control algorithm

把數據導出進行計算，可知其補償精度結果如表5所示。

表5 升沉補償系統仿真結果精度結果Table 5 Precision results of heave compensation system simulation results

從表5可以看出，模糊控制算法的精度要優于傳統PID控制算法的精度，尤其是在不規則海浪波下，模糊控制算法的優勢更能被體現。

6 結論

針對采礦船升沉運動引起的縱向動力響應問題，提出了一種主被動復合式的升沉補償系統。并從控制算法的角度對其進行分析，設計了模糊控制算法，在Simulink中分規則海浪波和不規則海浪波下進行仿真和比較，同時把模糊控制算法的仿真結果和傳統PID控制的算法仿真結果進行比較，得出以下結論。

(1)在規則海浪波下，傳統PID控制的補償精度在為90.4%；模糊PID控制的補償精度為93.2%，模糊控制補償精度比傳統PID控制的補償精度高3.2%。

(2)在不規則海浪波下,傳統PID控制的補償精度在為91.5%；模糊PID控制的補償精度為98.2%，模糊控制補償精度比傳統PID控制的補償精度高7.1%。

(3)模糊控制算法的精度優于比傳統PID控制算法的精度，尤其在不規則波下，更能體現模糊控制算法的優勢。