基于動力吸振器的EMS型磁浮車輛-軌道梁耦合振動抑制方法研究
周 陽,胡俊雄,陳曉昊,馬衛華,羅世輝
(西南交通大學 牽引動力國家重點實驗室,四川 成都 610031)
自20世紀60年代開始,德國、日本等國相繼開展了磁懸浮列車的技術研究。當前國際上已形成較成熟的常導電磁型和低溫超導磁懸浮交通技術體系。德國TR(Transrapid)是最具代表性的高速常導磁浮車輛系統,至今共研發了9代車型。目前,已有日本東部丘陵線(TKL線)、韓國仁川機場線、中國長沙磁浮機場線及北京磁浮S1線實現商業運營[1-2]。
EMS型磁浮車輛采用電磁主動懸浮,本質上是不穩定的,并且由于EMS型磁浮列車多采用高架線路運行,軌道梁發生彈性變形時易誘發特殊的車-軌耦合振動現象。國內外學者針對車軌耦合振動問題進行了大量的研究。20世紀70至90年代,Wilson、Cai等[3-4]建立了只考慮沉浮運動的車輛模型,并將電磁力等效為彈簧阻尼器,研究分析了不同車速以及不同梁型的耦合響應;Yau等[5]建立了由車載PI控制器控制的雙自由度磁浮車輛與柔性軌道耦合的動力學模型,并提出了新的迭代計算方法,研究分析了車速、磁浮列車垂向加速度對耦合振動的影響;Lee等[6]建立了5自由度的主動控制磁浮車輛-柔性軌道的垂向動力學模型,采用數值分析的方法分析了軌道不平順、車速、軌道梁跨距等參數對懸浮穩定性的影響;高精隆等[7]分析了吸振器的質量以及阻尼對系統振動的影響,建立了多種數學模型的運動方程,研究了在有無動靜質量時系統的減振效果;殷永康等[8]按照目前的技術原理、剛度調整范圍以及對應的速度等性能進行了分析和比較,最后提出一種采用錐螺旋彈簧的變剛度的半主動吸振結構;李曉龍等[9]提出了通過設置非線性飽和環節、動態調整飽和閾值來抑制車軌耦合振動的新方法,系統在平衡點附近時通過調整飽和閾值來改變控制輸出的幅值特性,逐步消除引起共振的能量,從而達到抑制振動的目的;汪科任等[10]采用AHP(層次分析法)求取系統二次型性能指標中狀態加權矩陣的權重系數,建立了2種狀態反饋控制器,為懸浮控制器的優化設計提供一定的參考。
本文主要采用動力吸振器作為車-軌耦合振動的制振措施。動力吸振器(Dynamic Vibration Absorber)由輔助質量、彈簧以及阻尼組成,屬于抑制共振的被動式制振器,又稱調諧質量阻尼器TMD(Tuned Mass Damper)。其基本原理是在振動對象以外建立一個附加的動力學系統,將制振對象的振動響應吸收并消耗在阻尼元素中。動力吸振器在各個工程領域中運用廣泛,國內外學者也做了很多研究。劉海平等[11]利用歐拉屈曲梁作為彈簧元件,采用復變量平均法,求解了不同類型非線性吸振器模型的解析解。趙艷影和徐鑒[12]對兩自由度系統采用多尺度法研究了時滯非線性動力吸振器對主系統的減振性能,得到了主系統的振幅-時滯響應曲線。研究結果表明,對時滯非線性動力吸振器,可以通過調節反饋增益系數和時滯控制主系統的振動。李俊等[13]將簡諧激振下無阻尼單自由度主系統的動力消振原理推廣到多頻諧波激勵下無阻尼多自由度主系統的情況。
本文以某中低速空簧中置式磁浮列車為研究對象,建立了8自由度的車-軌耦合垂向動力學模型,采用基于位移-速度-加速度反饋的PID主動控制,基于擴展定點理論與頻率傳遞函數分析單動力吸振器和多重動力吸振器方案的最佳參數,進而對不同質量比的動力吸振器進行動力學仿真對比。在研究單自由度系統和多模態系統動力吸振器的最佳參數的基礎上,分析不同速度下2種減振措施的制振效果。
1 動力學建模
1.1 磁浮車輛模型
某中低速磁浮列車每節車體通過6個空氣彈簧支撐在3個懸浮架上,空氣彈簧安裝于縱梁中間位置。懸浮電磁鐵由內外極板以及線圈、鐵芯組成,2個線圈為一組,再通過間隙傳感器和懸浮控制器構成一套閉環控制系統,一般稱之為一個控制單元或控制點,建模過程將單個懸浮架的懸浮力集中在懸浮架前后端點處。本文主要分析磁浮車輛-懸浮控制-軌道梁-動力吸振器系統的垂向動力學響應,因此將車輛簡化為由車體、懸浮架組成的剛體系統,僅考慮車體和懸浮架的垂向和點頭運動自由度,建立的8自由度的磁浮車輛垂向動力學模型如圖1所示。
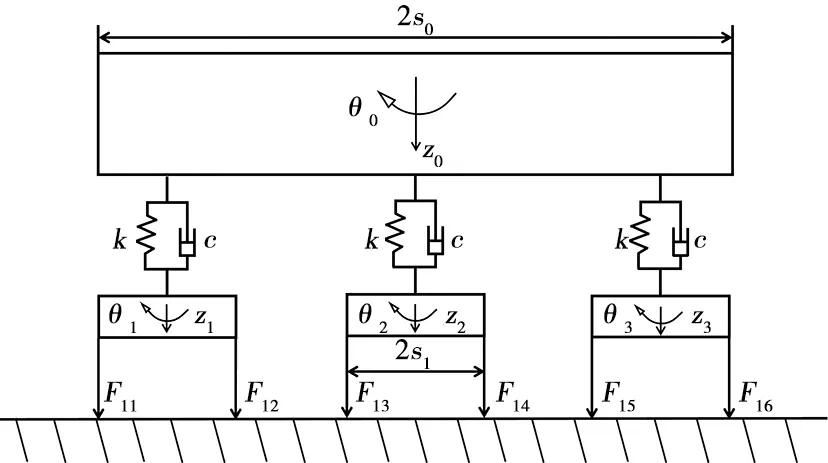
圖1 磁浮車輛垂向動力學模型
磁浮車輛垂向動力學方程如式(1)~式(8)所示。
車體沉浮運動:
(1)
式中:M——車體質量;


z0——車體垂向位移;
k——二系懸掛剛度;
c——二系懸掛阻尼;
z1,z2,z3——懸浮架1,2,3的垂向位移。
車體點頭運動:
(2)
式中:J——車體轉動慣量;


θ0——車體角位移;
s0——車體半長;
s1——懸浮架半長。
懸浮架1沉浮運動:
(3)
懸浮架1點頭運動:
(4)
懸浮架2沉浮運動:
(5)
懸浮架2點頭運動:
(6)
懸浮架3沉浮運動:
(7)
懸浮架3點頭運動:
(8)
式中:J1,J2,J3——懸浮架1,2,3的轉動慣量;
F11~F16——懸浮架對應的懸浮力。
1.2 無動力吸振器(TMD)時軌道梁模型
中低速磁浮交通軌道梁大多為簡支梁,本文采用只考慮梁彎曲變形、不考慮剪切變形及轉動慣量影響的歐拉-伯努利梁(Euler-Bernoulli beam)模擬軌道梁。動力學模型建立在以下假設條件的基礎上:(1)忽略梁的結構阻尼;(2)僅考慮軌道梁在垂向上的受力及動力作用情況;(3)軌道梁為等截面梁,且材質均勻;(4)軌道梁的運動滿足小變形理論并在彈性范圍內。軌道梁的振動微分方程為:
(9)
式中:E——軌道梁彈性模量;
I——橫截面的截面慣性矩;
EI——軌道梁抗彎剛度;
ρ——軌道梁線密度;
Q——軌道梁的外作用力;
x——外力作用位置。
利用模態疊加法,將軌道梁的位移分解為i階模態下的廣義坐標與形函數的乘積:
(10)
式中:φi(x)——軌道梁的i階振型函數;
qi(t)——軌道梁的i階模態坐標。
將式(10)代入式(9)中得:
(11)
將式(11)兩邊同時乘以φn(x),并沿軌道梁全長進行積分:
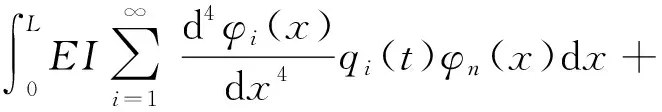
(12)
由于主振型的正交性,當i≠n時,方程(12)左側兩項均為0,因此方程(12)可簡化為:
(13)
由簡支梁的邊界條件可求得振型函數:
(14)
由于本文主要研究單跨簡支梁的1階振動影響,代入式(14)整理可得簡支梁受迫振動的響應結果:
(15)
式中:Pj(t)——第j個電磁力的大小;
xj是——第j個電磁力的位置;
L——軌道梁跨距;
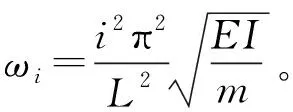
1.3 有動力吸振器(TMD)時軌道梁模型
圖2為帶TMD的軌道梁模型。
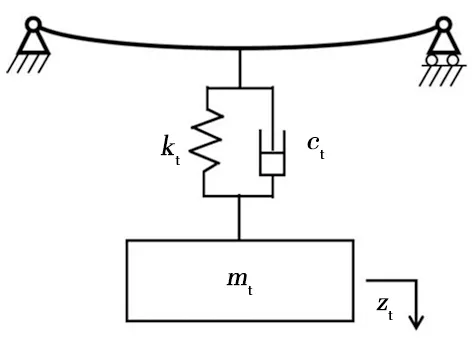
圖2 帶TMD的軌道梁模型
由式(14)可知,只考慮軌道梁的1階振動時最大變形位置為跨中處,所以選擇在跨中設置TMD,則TMD的運動方程為:
(16)
將式(10)、式(14)代入可得:
(17)
式中:mt——TMD質量;
kt——彈簧剛度;
ct——阻尼系數;
zt——垂向位移。
此時軌道梁的運動方程為:
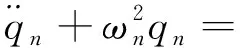
(18)
1.4 軌道不平順
國內外對線路不平順研究較多,但并不統一,本文采用文獻[14]中擬合的磁浮高低線路不平順功率譜,其數學表達式為:
(19)
式中:Ω——空間頻率,m-1;
A,B,C,D,E,F,G——特征參數。
特征參數具體值如下:
A=0.003 782,B=-0.087 513,C=0.001 952,D=-0.213 341,E=0.017 071,F=-0.000 607,G=8.074 24×10-6。
采用三角級數法進行軌道譜反演,得到的磁浮軌道垂向不平順時域圖如圖3所示。
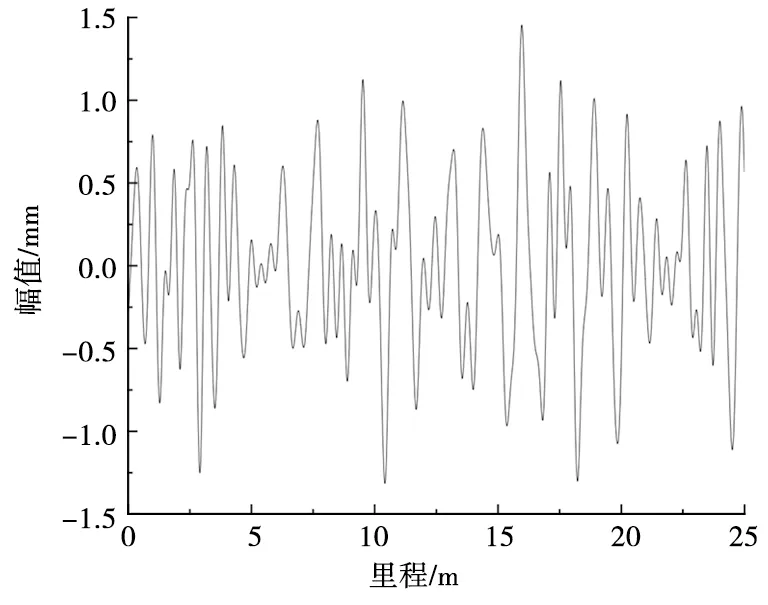
圖3 磁浮軌道高低不平順時域圖
1.5 懸浮控制模型
本文采用基于位移-速度-加速度反饋的PID主動控制,狀態觀測器如圖4所示。
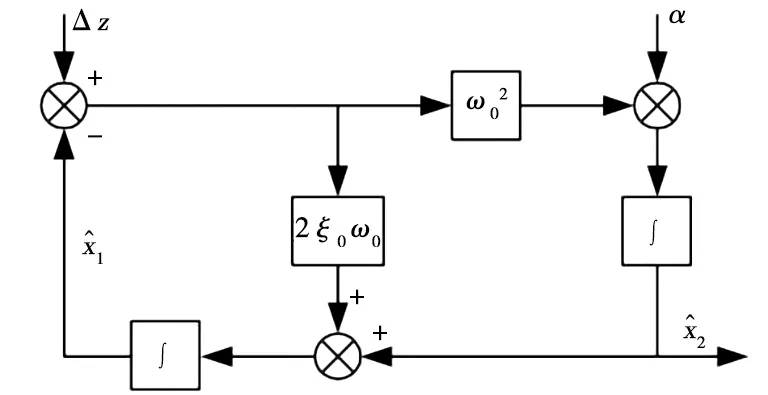
ω0.觀測器的特征頻率;ξ0.觀測器的阻尼。圖4 狀態觀測器
控制器中位移和加速度直接反饋,速度則通過觀測器中加速度與位移信號構造而成。控制器電流方程:
(20)
式中:KP、Kv、Ka——分別為PID中位移、速度、加速度反饋系數;
Δz——懸浮間隙位移變化值;


當懸浮間隙在額定間隙處小范圍波動時,懸浮力公式為:
(21)
式中:μ0——真空磁導率;
A——磁極面積;
N——線圈匝數;
i0,c0——額定懸浮電流和額定懸浮間隙。
將式(20)代入式(21)即可得實際作用懸浮力:
(22)
2 動力吸振器設計
2.1 單動力吸振器設計
由于動力吸振器的阻尼系數要比軌道梁結構阻尼對軌道梁動力響應的影響大,所以忽略軌道梁的結構阻尼,針對軌道梁1階模態進行制振,此時軌道梁系統近似為無阻尼單自由度系統。動力吸振器與軌道梁等效系統如圖5所示。
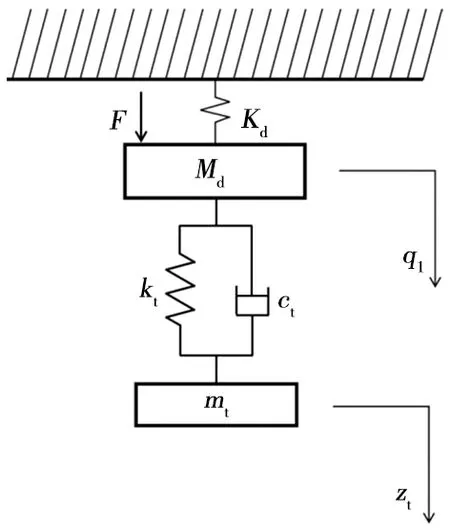
圖5 動力吸振器與軌道梁等效系統φ1(ω)=arctan
將軌道梁上外力改寫為Fejωt,求解方程可得軌道梁和動力吸振器的振幅比與相位:
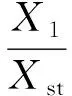
(23)
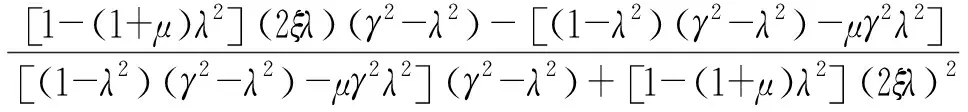
(24)
式中:μ——質量比,μ=mt/ρL;
ξ——阻尼比,ξ=c/(2mω1);
Xst——軌道梁靜變形,Xst=F/Kd;
λ——強迫振動頻率比;
γ——固有角頻率比。
對式(23)兩邊取平方,并將ξ前系數化為1,則:
(25)
當ξ=0時,振幅比為:
(26)
當ξ=∞時,振幅比為:
(27)
當式(26)等于式(27)時,式(25)與ξ無關,此時式(25)化簡為:
(28)
此時式(27)與式(28)相同,振幅比與ξ無關的點就是ξ=0與ξ=∞ 2條曲線的交點,如圖6所示。因此可以利用定點現象進行動力吸振器參數設計。
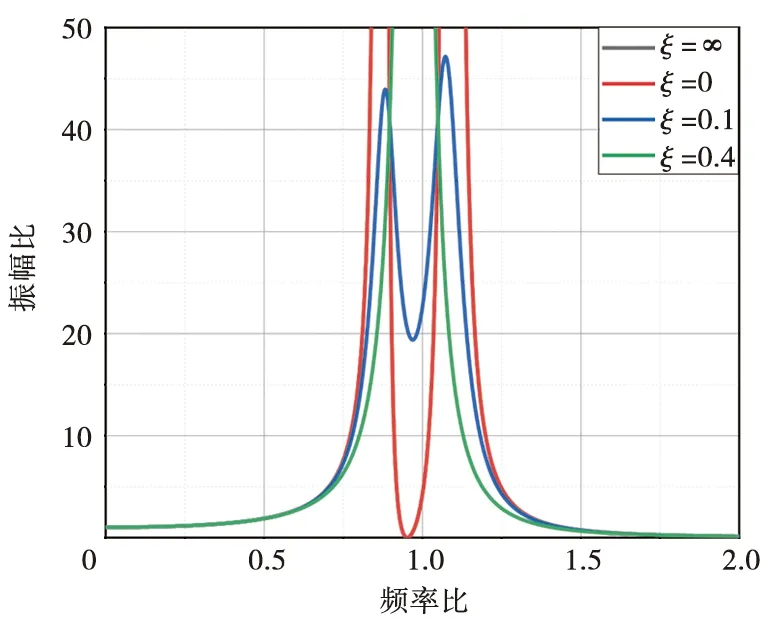
圖6 不同阻尼比下振幅比曲線
利用擴展定點理論可以得到動力吸振器最優參數的2個條件:
最優同調條件(2個定點等高):
(29)
最優阻尼條件(定點處最大阻尼):
(30)
滿足這2個條件后,主振動系統的最大振幅比:
(31)
將式(29)、式(30)代入式(23)中得:
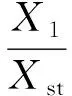
(32)
由式(32)可知,動力吸振器的設計目標簡化為對質量比單參數的選擇,具體關系如圖7所示。
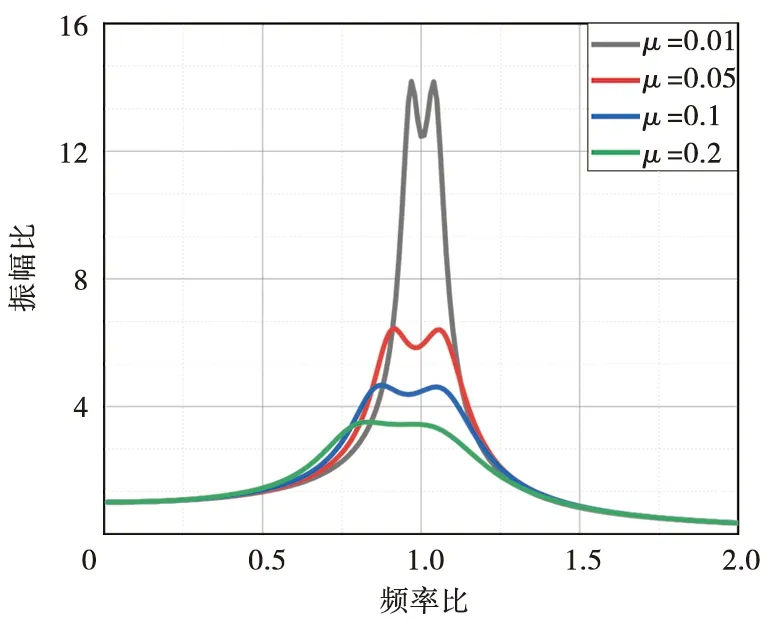
圖7 振幅比與質量比的關系
阻尼與頻率按照上述公式選取,當外部激勵頻率與主振動系統的固有頻率接近時,振幅比增大;振幅比最大值隨著質量比的增大而衰減,可見增大質量比可以提高抑振效果,但是過大的質量比會使得整體系統過重,從而使得軌道梁靜撓度增大,所以本文將質量比限制在0.2以下。
根據上述條件,針對軌道梁1階振動,可以得到動力吸振器3個參數的設計公式:
(33)
2.2 多重動力吸振器設計
考慮軌道梁第i階模態,針對第i階模態的軌道梁-動力吸振器系統的力學模型如圖8所示,圖中kdi、cdi、mdi分別為針對第i階模態動力吸振器的剛度、阻尼系數和質量。
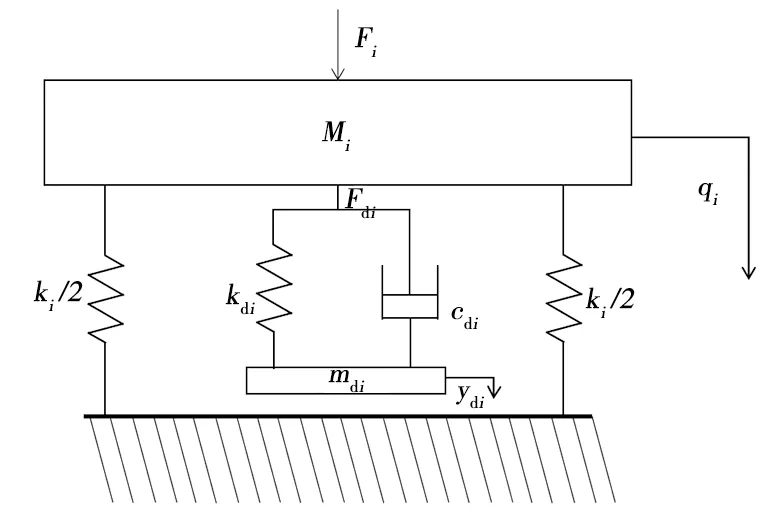
圖8 力學模型圖
由動力吸振器產生的反饋力Fdi可以表示為:
(34)
包含動力吸振器的第i階模態傳遞函數表達式為:
(35)
其中,
(36)
(37)
(38)
(39)
對于控制多模態的動力吸振器的設計問題可以以各個模態為單位獨立考慮。將單自由度系統的最優設計法與模態控制理論相結合,可以將單自由度系統動力吸振器的最優設計推廣至i階模態制振中,由此可得針對i階模態的最優設計。
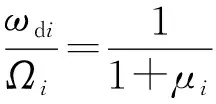
(40)

(41)
軌道梁前2階模態如圖9所示。
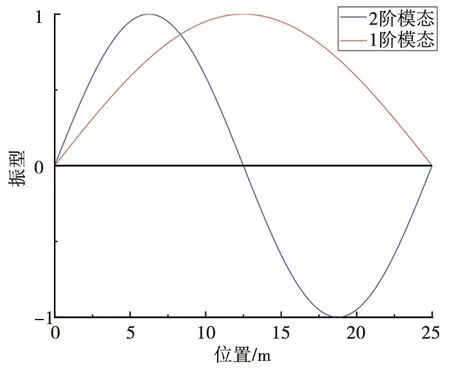
圖9 前2階模態圖
可見,模態變形最大位置分別在L/4、L/2以及3L/4處。因此選擇在3個模態變形最大位置各安裝一個動力吸振器,動力吸振器的參數按照式(9)、式(10)設計,但L/4和3L/4處的動力吸振器針對軌道梁第2階固有頻率設置參數,L/2處的動力吸振器針對軌道梁第1階固有頻率設置參數。
此時多重TMD(MTMD)動力學方程為:
(42)
(43)
(44)
3 仿真結果分析
聯立車輛-懸浮控制-軌道梁-吸振器動力學方程組,選取軌道梁五階模態,建立垂向車-軌-吸振器耦合動力學模型,部分參數見表1。

表1 垂向車-軌-吸振器耦合動力學模型參數表
根據最優同調和最優阻尼調整TMD的參數,取TMD與橋梁的質量比為0.01、0.03、0.05、0.1和0.2進行對比分析。單個TMD跨中撓度、加速度以及抑振效果對比結果如圖10、圖11所示。多重TMD(MTMD)跨中撓度、加速度以及抑振效果對比結果如圖12、圖13所示。

圖10 TMD對跨中撓度影響及抑制效果

圖11 TMD對振動加速度影響及抑制效果
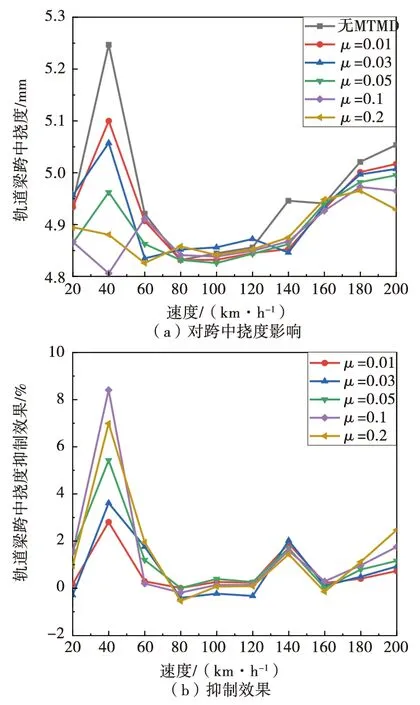
圖12 MTMD對跨中撓度影響及抑制效果
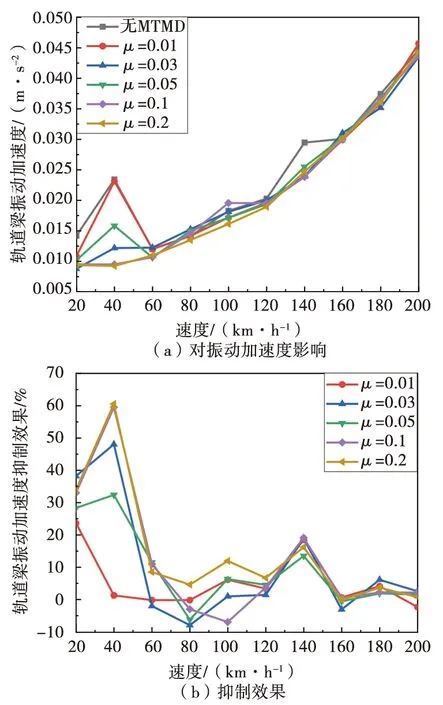
圖13 MTMD對振動加速度影響及抑制效果
由圖10、圖11分析可知:(1)模型中單個懸浮架前后懸浮控制點距離為1.7 m,當速度為40 km/h時,懸浮控制對軌道梁激擾力的頻率為(40/3.6)/1.7=6.536(Hz),非常接近軌道梁1階固有頻率(6.443 Hz),因此此時軌道梁動態響應較大,并且TMD的抑振效果隨著質量比的增大而增大,當質量比為0.1時,位移抑制效果最好,接近7%,當質量比為0.2時,振動加速度抑制效果最好,接近60%;(2)當速度在60~160 km/h之間時,小質量比的TMD抑振效果比大質量比的TMD的抑振效果要好,這是由于列車運行頻率遠離軌道梁固有頻率,因此軌道梁動態響應比較平穩且響應值較小,所以大質量比的TMD產生了較大的靜撓度導致了位移抑制產生負控制;(3)當速度大于180 km/h時,軌道梁動態響應隨著速度增大而增大,位移抑制效果也隨著質量比的增大而增大,但是較大的質量比會導致軌道梁振動加速度變大。由圖12、圖13可知,采用多重TMD時,當懸浮控制對軌道梁激擾頻率與軌道梁1階固有頻率接近,跨中撓度和振動加速度的抑制效果均超過了單TMD,最大抑制效果均出現在質量比為0.1的多重TMD控制下。此外,同等質量比下由于多重TMD質量分散在3個單TMD上,所以產生的負控制小于單TMD。
4 結論
本文將某中低速磁浮列車簡化為由車體、懸浮架組成的8自由度剛體系統,建立了基于位移-速度-加速度反饋的PID主動控制模型,基于擴展定點理論與頻率傳遞函數設計了單動力吸振器和多重動力吸振器,并分析了2種動力吸振器方案的最佳參數。通過對不同質量比的動力吸振器開展動力學仿真對比可以得出以下結論:
(1) 動力吸振器對軌道梁振動加速度的抑制效果顯著,但對軌道梁最大位移的抑制效果較小;
(2) 當激擾力頻率接近軌道梁固有頻率時,軌道梁因共振而達到最大動態響應,此時0.1質量比的多重動力吸振器的振動加速度抑制效果最好,接近60%,進一步增大質量比后,制振效果下降;
(3) 當激擾頻率遠離軌道梁1階固有頻率時,大質量比動力吸振器容易產生負控制,而過小的質量比會使得動力吸振器的抑振效果不明顯;
(4) 多重動力吸振器質量分布均勻,抑振效果優于單動力吸振器,并且負控制小于單動力吸振器。

