溫度效應對地鐵橋梁數據預測模型影響研究

朱 力 朱爾玉 張 衡 白正偉 安小詩

(1.北京市地鐵運營有限公司地鐵運營技術研發中心 北京 100089；2.北京交通大學 北京 100044)

1 引言

近些年國內外學者對橋梁工程健康檢測系統的研究逐漸增多，這也與我國橋梁工程發展階段有直接的關系[1]。影響健康監測系統數據預測精度的因素中溫度效應是主要的影響因素之一。

李全林[2]通過對日照下混凝土箱梁溫度場和溫度應力的研究，深入分析了溫度效應在橋梁健康監測系統中對數據預測的具體表現。在對橋梁結構監測數據的預測模型建立方面，Kaveh[3]、黃方林[4]等人均從不同的技術方面對橋梁健康監測系統展開了一系列研究。劉夏平等[5]研究了橋梁撓度監測中溫度效應的分離，嚴鵬[6]開展了橋梁檢測信號中的降噪工作。在對橋梁檢測系統中溫度效應的具體影響研究方面還有待更為深入地分析研究。

本文通過使用改良的數據預處理方法，實現了對地鐵橋梁高頻監測數據的預處理，克服了傳統方法對高頻數據剔除過度的問題；采用對監測數據和溫度效應的回歸分析，建立不同測項與溫度和溫差的回歸方程，使得溫度效應從監測數據中得到了分離；通過對基于溫度效應的ARMA預測模型和單因素ARMA預測模型的預測結果進行對比，得出了溫度效應對數據預測模型的影響是不可忽略的結論。

2 數據分析方法

2.1 數據預處理

2.1.1 傳統的3σ法的弊端

主要對以下方面進行對比:

(1)低頻數據最大值與最小值的差；

(2)傳統3σ法異常數據識別區間的長度；

(3)高頻數據最大值與最小值的差。

通過對比發現使用3σ準則計算得到的剔除區間是不符合動態數據實際變化規律的，會對列車經過時的數據造成錯誤剔除。

2.1.2 改良的3σ法方案的提出

在綜合比較了各個測點高低頻數據的變化范圍之后，本文對傳統3σ準則中方差σ2的計算方法進行了改進，將統計得到的方差σ2放大，來彌補監測數據中動態數據過少的問題。經過試算發現，當統計得到的方差σ2擴大4倍，即標準差σ擴大2倍時，異常值的識別區間可以較大程度地將列車經過時的峰值數據包含在內，不會將正常數據識別為異常值。根據動態數據修正的標準差為σD＝2σ，則基于動態數據的異常值識別區間范圍變為，當數據落于[ω2，ω1]區間之外時，數據被識別為異常值并剔除。

注1 一、二階異構多智能體系統一般包含多個一階系統和多個二階系統，而本文中系統式 (1) 與此略有差異，因此也可稱系統式 (1) 為“偽異構系統”，即異構系統的特殊化處理.

2.1.3 異常值插補方法的研究

由于地鐵橋梁健康監測數據有著變化趨勢明顯、數據量大且很少出現連續缺失值的特點，提出了改良的最近鄰插補法[8]。根據距離的權重使用缺失值附近k個有效值對缺失值擬合，權重根據距離反比分配，距離越近的數據權重越高，隨著距離增加權重降低。選擇缺失值的前n個值對其進行插補，則插補值的計算公式為:

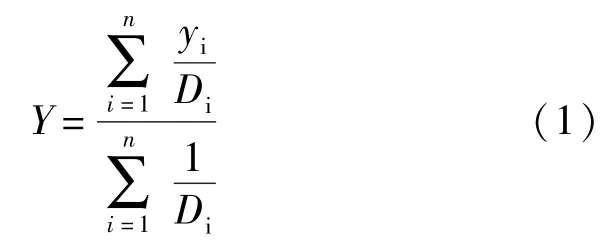
式中，yi為缺失值附近的有效值；Di為有效值到缺失值的距離；Y為插補值。

本文統一選用缺失值的前4個數據對缺失值插補，則具體的計算公式為:

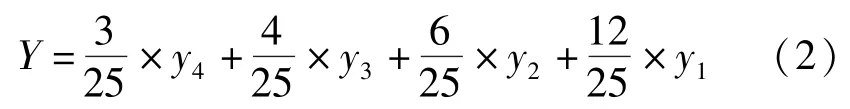
2.2 溫度效應與監測數據回歸分析

以2016年1月份到12月份北京地鐵某線連續梁橋的梁體縱向位移為例進行分析，其監測數據如圖1所示，期間監測的溫度值如圖2所示。通過對梁體位移數據和溫度數據圖像的對比可以看出梁體位移與溫度的變化趨勢十分相似。以溫度為橫坐標，梁體位移為縱坐標繪制圖形，可以初步判斷位移與溫度之間是存在線性關系的。為將溫度效應從監測項中分離，使用線性回歸模型[9]來確定溫度與監測項之間的關系。

圖1 北京地鐵某線119～120墩段梁體縱向位移

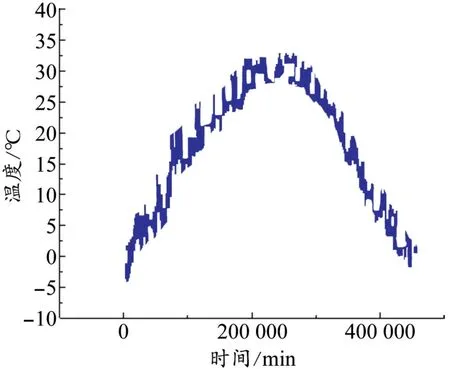
圖2 北京市2016年1月份到4月份溫度檢測值

假設監測項與溫度和溫差之間的線性回歸模型為:

式中，YT為溫度效應回歸的值；XT為監測的溫度數據；XΔT為溫差數據；a1為溫度項的系數；a2為溫差項的系數；b為常數項。當測項只與溫度存在回歸關系時，系數a2＝0；當測項只與溫差存在回歸關系時，系數a1＝0。

選用0:00～5:00之間地鐵停止運行的時間段的監測數據做回歸分析，其與溫度效應的回歸結果更準確。使用Matlab軟件來對溫度、溫差與監測項之間的回歸方程進行計算，部分統計結果如表1所示。

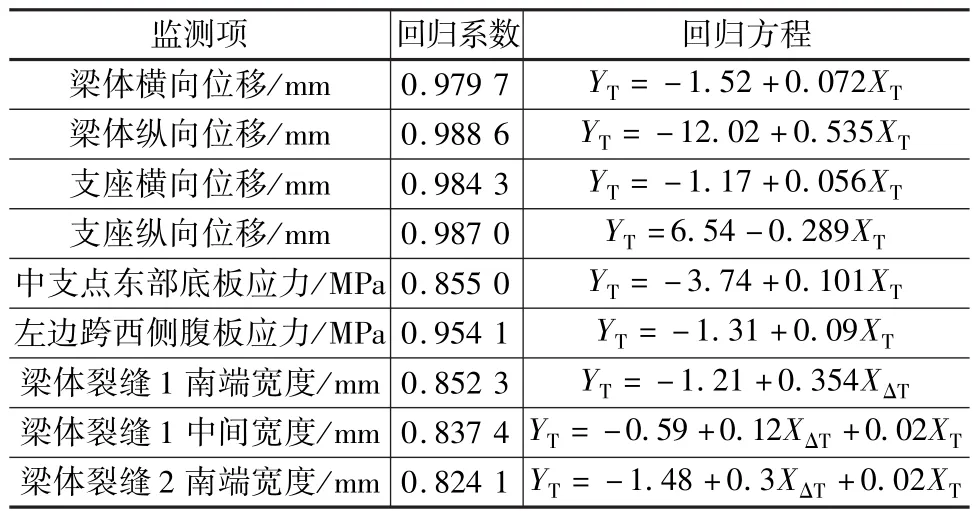
表1 不同測項與溫度和溫差的回歸方程

2.3 監測數據中分離溫度效應的研究

梁體位移、應變等數據主要受溫度變化、風荷載與列車荷載的影響，本文研究的橋梁均為中小跨徑橋梁，未考慮風荷載對橋梁位移、應變等其他測項的影響，則監測數據的變化主要受溫度變化與列車荷載的影響，如式(4)所示:

式中，Y為梁體位移、應變等監測值；YT為溫度引起的變化量；YV為列車荷載引起的變化量。

以梁體縱向位移為例，對數據的溫度效應進行分離。由于其對溫度的回歸方程為:

YT＝-12.02＋0.535XT

原始監測數據中減去溫度代入回歸公式即可將數據中溫度影響去除，即Y-YT。

原數據由于溫度效應的存在，自身是存在趨勢性的，而且分離出溫度效應之后的數據，位移的變化更趨于隨機，相反趨勢性明顯減弱。

使用自相關系數來評價分離溫度效應后數據的平穩性，在做差之后，數據的前五百階自相關系數由做差前的0.98左右減小到0值附近，說明數據平穩性顯著增加。

其做差前后的前五百階自相關系數分別見圖3和圖4。將分離溫度效應后的數據再與溫度計算相關系數，得到的值在0.01以下。結合趨勢性與平穩性分析，此種分離溫度效應的方法可以使得處理后的數據不再與溫度相關。

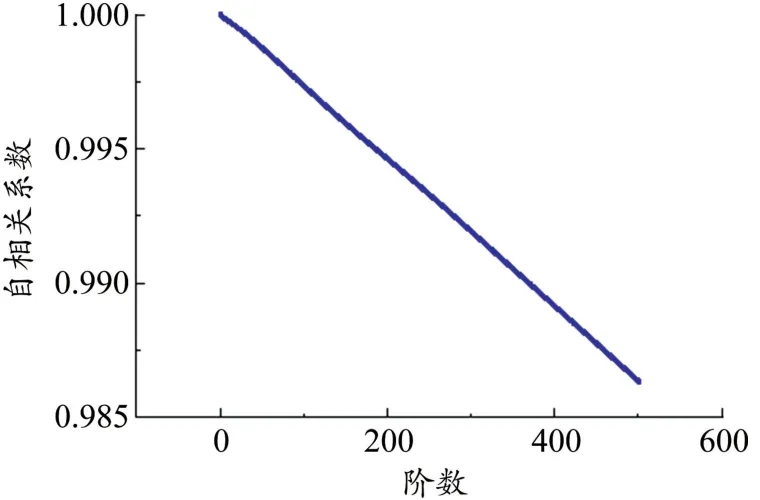
圖3 梁體縱向位移去除溫度效應前的自相關系數

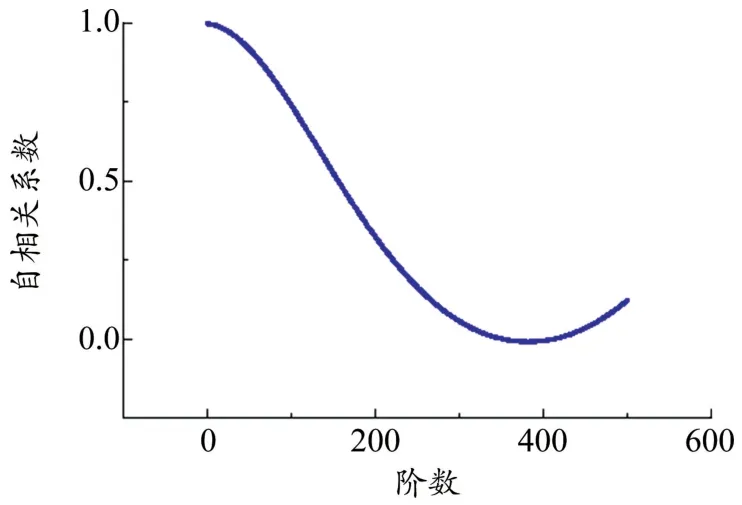
圖4 梁體縱向位移去除溫度效應后的自相關系數

3 預測模型的建立

基于溫度效應的預測模型將數據整體的趨勢變化分為了兩部分考慮，整體均值的變化趨勢由溫度效應來體現，而數據波動性則使用時間序列來對其建立數學模型來體現，將兩部分預測數據相結合即為最終的預測數據。從溫度和時間兩個方面對監測數據進行預測的模型，即為基于溫度效應的時間序列預測模型[10]。

4 預測結果對比分析

4.1 基于溫度效應的ARMA預測模型

在將預測數據與原始數據比對之前，需要將預測數據進行逆向標準化、逆向差分、回填溫度效應三步處理[11]?；靥顪囟刃墙o經過兩部處理后的預測數據加上溫度效應項。對原始數據的前4 195個數據進行預測，預測樣本與原始數據進行對比，觀察預測樣本的擬合效果，其對比圖見圖5。

圖5 訓練樣本與原始數據對比

將2016年1月2日中午12時的實測溫度代入到溫度效應，回填到ARMA模型預測的中午12時的預測數據當中，再與中午12時梁體縱向位移的實測數據進行比較，觀察預測數據的擬合效果。預測數據與實測數據的對比圖如圖6所示。梁體縱向位移的預測值與實測值相比較，預測值的變化趨勢與數值所在范圍與實測數據的大致類似，可以認為預測值能夠反映實際數據的變化規律。表2列出了120個數據中的前15個預測數據與實測值之間的相對誤差。

圖6 未來1 h預測數據與實測數據對比

表2 預測數據與實測值之間的相對誤差

4.2 ARMA預測模型結果分析

數據預處理過程與前文相同，但不進行分離溫度效應這一步驟。預測數據與實測數據對比如圖7所示。由于對未來數據進行的是無樣本預測，預測數據無法準確地給出數據的變化趨勢。隨著預測時長的增加，預測數據與實測數據之間偏差越來越大。同樣使用相對誤差來評判不考慮溫度效應的時間序列模型的預測效果。不考慮溫度效應的時間序列模型前15個預測數據與實測值之間的相對誤差如表3所示?？芍A測數據的前十幾個數據的相對誤差不太大，但是120個預測數據的相對誤差的絕對值的平均值為1.78%，最大相對誤差為3.96%，兩項指標均為基于溫度效應預測模型誤差的數倍。只考慮溫度效應，使用溫度的回歸模型作為單因素預測模型對數據進行預測。

圖7 時間回歸模型預測數據與實測數據對比

表3 時間回歸模型預測數據與實測值相對誤差

由于簡支梁橋的梁體縱向位移與溫差不存在回歸關系，其與溫度的回歸方程為:

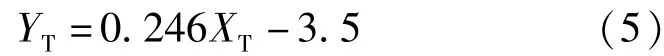
將2016年1月2日中午12時的溫度代入到溫度回歸方程中，溫度預測模型的預測數據與實測數據對比如圖8所示。前15個預測數據與實測值之間的相對誤差如表4所示。

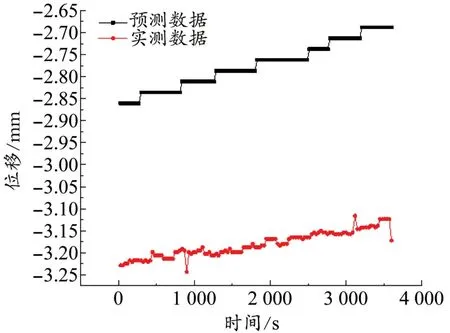
圖8 溫度回歸模型預測數據與實測數據對比

由表4可知預測數據相對誤差較大，120個預測數據的平均誤差為12.80%，最大相對誤差為15.27%。

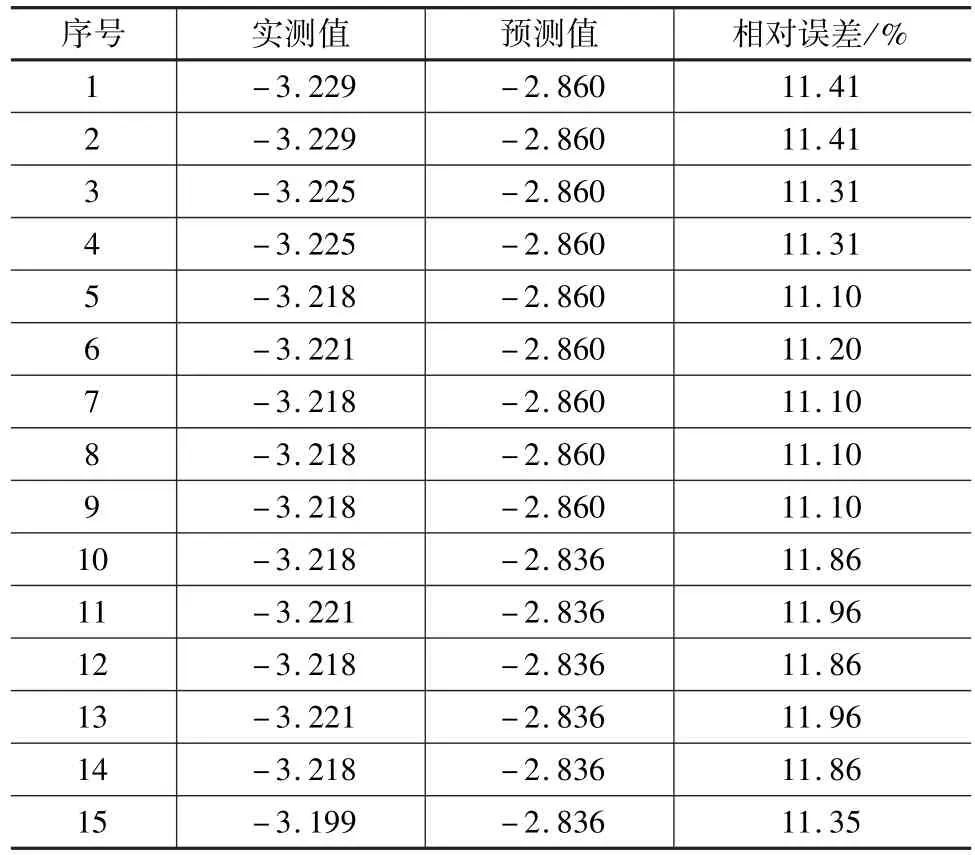
表4 溫度回歸模型預測數據與實測值相對誤差

基于溫度效應的時間序列預測模型的準確度是相當高的。計算120個數據的相對誤差的絕對值平均值為0.50%，其中最大相對誤差為1.04%；僅考慮單因素的時間序列模型誤差的絕對值平均值為0.61%，其中最大相對誤差為1.59%；而僅考慮溫度效應的預測模型誤差的絕對值平均值達到了11.46%，其中最大相對誤差為11.96%。

5 結束語

(1)通過對傳統的數據預處理方法進行改進，解決了傳統數據預處理方法無法準確處理橋梁高頻監測數據的問題，并通過將方差放大得到可應用于橋梁高頻監測數據處理的改良版3σ法和異常值插補法。

(2)通過溫度效應對橋梁監測數據的影響分析，建立了基于溫度效應的不同測項與溫度和溫差的回歸方程，建立了一種高效的分離溫度效應的機制。

(3)通過ARMA時間序列模型對數據進行預測，并將預測結果與基于溫度效應的ARMA時間序列模型預測得到的預測結果進行了比較，得出了基于溫度效應的ARMA時間序列模型預測效果更好的結論，并證明了溫度效應對預測模型建立不可忽視的影響。