交錯桁架鋼框架結構抗震設計方法研究

周緒紅，周志彬，周期石?，黃偉，楊夢圓

（1.中南大學土木工程學院，湖南長沙 410083；2.重慶大學土木工程學院，重慶 400045）

交錯桁架鋼框架結構體系由柱、鋼桁架、縱向框架梁和樓板組成，因結構中包含較多的軸心受力構件，與傳統框架結構體系相比，能更有效地發揮材料性能，使結構用鋼量顯著降低.交錯桁架鋼框架結構體系中的桁架可采用混合式桁架、空腹式桁架或帕式桁架等，其中混合式桁架由于結構剛度適中且建筑上能提供內廊，其應用最為廣泛［1］.

已有試驗研究表明［2-5］，混合式交錯桁架鋼框架結構在低周往復荷載作用下表現為斜腹桿失效的脆性破壞特征，抗震性能較差.如何改善混合式交錯桁架結構抗震性能已成為近年來該結構的研究熱點，改進思路主要有兩種：一是在不改變傳統桁架形式的基礎上，將混合式桁架空腹節間的弦桿設置為耗能段，以提高結構的抗震性能.美國鋼結構協會發布的交錯桁架體系設計指南［6］中指出桁架空腹節間弦桿可以作為耗能構件，前提是需要保證斜腹桿一直處于彈性狀態，但指南中未提出實現空腹節間弦桿耗能的設計計算方法.文獻［7］基于能量平衡對交錯桁架延性區段空腹節間弦桿進行了塑性設計，并采用傳統桁架簡化計算模型［6，8-9］對交錯桁架的非延性區段構件進行彈性設計，由于傳統桁架簡化計算模型假定弦桿僅在空腹節間及與空腹節間相鄰的節間連續、其余節間為鉸接，其計算結果誤差較大且此計算模型中受力最不利的腹桿即與空腹節間相鄰的斜腹桿軸力計算值比真實值偏小；二是在傳統交錯桁架結構中增設耗能元件.如趙寶成等［10］在交錯桁架中內填Y 形偏心腹桿，試驗表明偏心腹桿式交錯桁架滯回曲線比較飽滿，結構的耗能能力較強.Kim等［11-12］提出了在交錯桁架結構底層支撐和第2 層中部斜腹桿處設置防屈曲支撐或在桁架空腹節間設置摩擦阻尼器的方法，分析結果表明該方法能有效提高結構延性系數和極限層間位移角，降低結構的失效概率，增設耗能元件可有效提高交錯桁架鋼框架結構的抗震性能，但與空腹節間弦桿耗能結構相比，構造相對復雜.

在結構抗震設計中，為實現結構“大震不倒”的設防目標，一般采用彈塑性層間位移角限值確保結構在罕遇地震下的最大變形不超過其極限變形［13］，與一般鋼框架結構相比，交錯桁架鋼框架結構橫向抗側剛度大，彈塑性層間極限位移相對較小，一般鋼框架結構的彈塑性層間位移角限值不適用于交錯桁架鋼框架結構.

為實現交錯桁架鋼框架結構延性破壞的設計目標以及“大震不倒”的抗震設防目標，本文基于空腹節間弦桿耗能的設計思路，采用更為精確的水平荷載作用下桁架桿件內力計算模型，推導桁架腹桿內力計算公式，建立桁架腹桿設計內力調整方法，并基于桁架彈塑性變形分析，提出交錯桁架鋼框架結構彈塑性層間位移角限值計算方法.

1 交錯桁架鋼框架結構破壞模式

在桁架方向水平地震作用下，交錯桁架鋼框架結構的層間剪力主要由鋼桁架承受（見圖1），一般可能出現兩種不同的破壞機制（見圖2）：斜腹桿失效導致桁架喪失水平承載力進而引發整體破壞；桁架空腹節間弦桿截面轉角達極限轉角導致結構整體破壞.

圖1 交錯桁架鋼框架結構Fig.1 Steel staggered truss framing systems

圖2 交錯桁架結構兩種典型破壞模式Fig.2 Two typical failure modes of staggered truss structure

交錯桁架鋼框架結構中斜腹桿為軸心受力構件，屈曲后將迅速喪失承載力，因斜腹桿失效導致的結構整體破壞屬脆性破壞.空腹節間弦桿在水平力下為受彎構件，在罕遇地震作用下構件端部形成塑性鉸，可有效地耗散地震能量，提高結構的延性，因弦桿失效導致的結構整體破壞屬延性破壞.因此，在交錯桁架鋼框架結構抗震設計中應避免斜腹桿屈曲，并使空腹節間弦桿出現塑性鉸，以提高結構的耗能能力和延性.

2 桁架腹桿設計方法

交錯桁架鋼框架結構的抗震設計思路是使結構在罕遇地震作用下僅在桁架空腹節間弦桿處出現塑性鉸，其余構件均不發生屈曲且保持彈性狀態，即形成圖2 中“弦桿破壞”的結構失效模式.為了實現這種理想的結構失效模式，需要對已滿足“小震不壞”的桁架桿件進行設計內力調整，并使桁架斜腹桿在罕遇地震作用下不發生屈曲和保持彈性.

2.1 水平地震力下腹桿內力計算模型及方法

在水平地震力作用下，傳統桁架簡化計算模型［9］假定空腹節間及其相鄰節間弦桿為連續，其余節間弦桿為鉸接，計算較為簡便.下文算例表明，傳統桁架簡化模型由于忽略了遠離空腹節間弦桿的剪力和彎矩，導致腹桿軸力計算值偏差較大.

為了更準確地反映桁架桿件的實際受力狀態，本文建議選取如圖3（a）所示的弦桿完全連續的桁架內力計算模型，采用均布線荷載模擬地震作用下桁架所承受的水平力，根據桁架結構對稱布置、荷載為反對稱荷載的特點，可取圖3（b）所示的隔離體進行內力分析.

分析圖3（b）所示隔離體，并假定空腹節間上下弦桿所受剪力V相等［6，8］，根據力矩平衡可知其剪力V為：

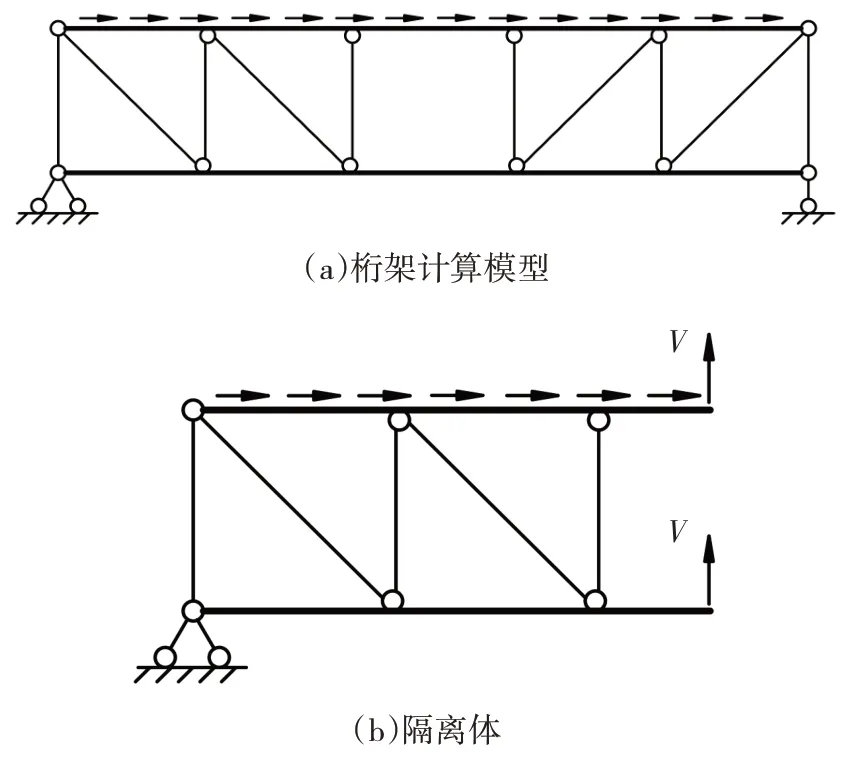
圖3 本文建議的水平力作用下桁架內力計算模型Fig.3 The calculation model of truss internal force under horizontal force suggested in this paper

式中：h為桁架高度；L為桁架長度；F為桁架所承受的水平力.

將上下弦桿等效為兩根帶懸臂的連續梁，可得上下弦桿彎矩圖和剪力圖如圖4 所示，圖中，Lw為桁架帶斜腹桿節間長度，Lv為空腹節間長度.

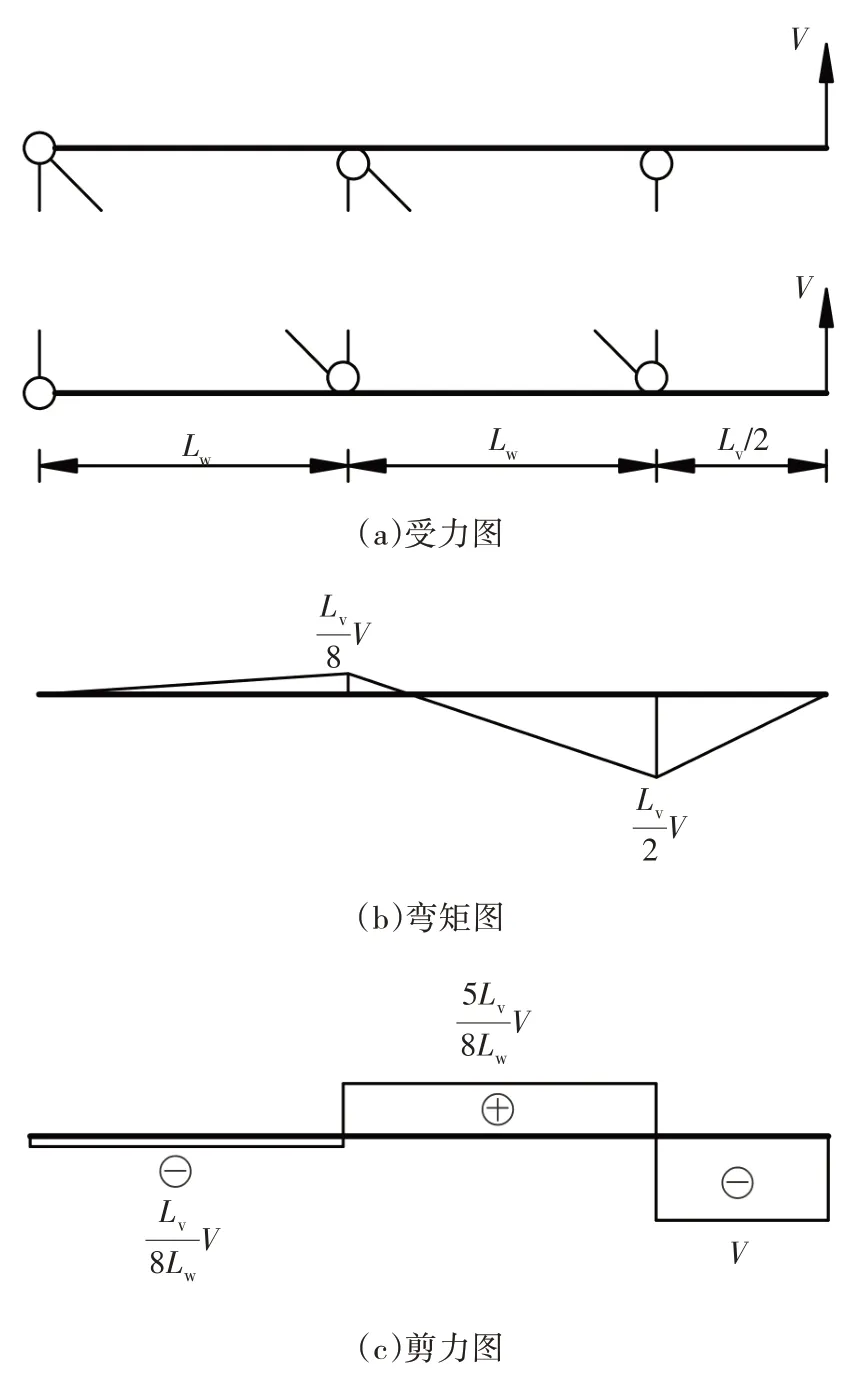
圖4 桁架弦桿內力圖Fig.4 Internal force diagram of chord members

根據弦桿等效連續梁模型求得的各支點反力可以反算得到腹桿軸力如圖5 所示，圖中，α為斜腹桿與水平面夾角.

圖5 左半桁架腹桿軸力Fig.5 Axial force of web members of left half truss

從圖5 中可看出，水平力并非按斜腹桿剛度分配到每根斜腹桿，這是由于桁架上下弦桿并非剛體，空腹節間及靠近空腹節間的弦桿彎曲變形相對較大，因此，靠近空腹節間的斜腹桿受力明顯大于遠離空腹節間的斜腹桿.

為驗證圖5 所示腹桿計算公式的準確性，采用有限元軟件SAP2000 建立了一榀桁架的有限元模型.桁架跨度為15 m，所有節間長度均為3 m，各構件的截面尺寸見表1，樓板跨度6 m，厚度為120 mm.桁架下弦桿與樓板通過節點相連，并約束樓板的位移UX和UZ，模擬樓板的支承；在桁架上弦桿端部約束Y向位移模擬上層樓板對桁架的側向支承，并在桁架柱腳處約束豎向和Y向位移，具體邊界條件如圖6所示.上層樓板傳來的水平力以均布線荷載的形式施加在桁架上弦桿，在桁架上弦桿施加合力為1 000 kN的均布線荷載.圖6 中①號、②號、③號和④號腹桿軸力的傳統桁架簡化計算模型分析結果、按本文式（1）和圖5中公式計算結果及有限元分析結果見表2.

表1 桁架截面尺寸Tab.1 Sections and dimensions of members of truss

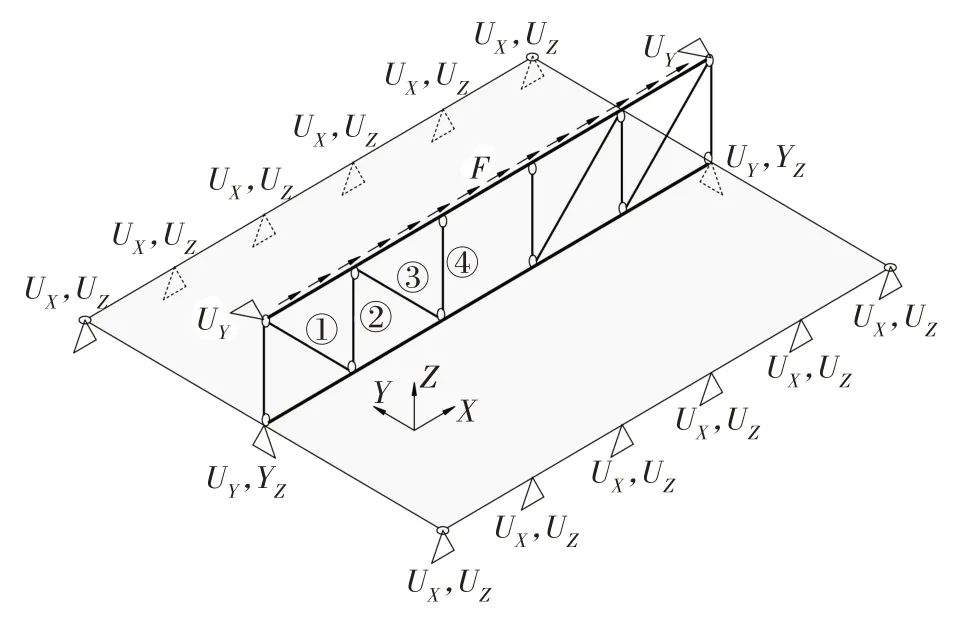
圖6 有限元模型示意圖Fig.6 Schematic diagram of finite element model

表2 腹桿軸力計算結果對比Tab.2 Comparison of axial force calculation results of web members

從表2 中可看出，按傳統桁架簡化計算模型得到的腹桿軸力誤差較大，且受力最不利的③號斜腹桿軸力計算結果小于有限元分析結果.本文提出腹桿內力的計算模型及推導的計算公式計算結果與有限元分析結果更為接近，且受力最大的斜腹桿計算軸力略高于有限元分析結果，滿足工程精度的同時使結構偏于安全.

2.2 腹桿設計內力調整方法

為實現交錯桁架鋼框架結構“強腹桿弱弦桿”的設計原則，需要對小震作用下桁架腹桿的計算內力進行調整，以保證在罕遇地震作用下空腹節間弦桿先于斜腹桿發生破壞.

當桁架空腹節間弦桿在罕遇地震作用下產生塑性鉸時，若不考慮塑性鉸強化，可以認為此時桁架水平承載力達到最大，同時空腹節間弦桿剪力V也達到最大剪力Vp：

式中：Lvn為桁架空腹節間弦桿凈跨度；Mp為空腹節間弦桿的塑性鉸彎矩，可參考我國《高層民用建筑鋼結構技術規程》（JGJ 99—2015）［14］對偏心支撐耗能梁段承載力的規定取為全塑性受彎承載力.

式中：Wp為弦桿對其水平軸的塑性凈截面模量；f為鋼材強度設計值.當樓板與弦桿組合效應不可忽略時，計算Mp還需考慮弦桿-樓板組合效應的放大作用，可參考《高層民用建筑鋼結構技術規程》（JGJ 99—2015）［14］中對兩側帶樓板框架梁的規定取放大系數為1.5.

將Vp代入圖5 所示腹桿軸力計算公式，并對腹桿軸力與重力荷載代表值作用下的腹桿軸力進行組合，得到調整后的腹桿軸力設計值Nw，com為：

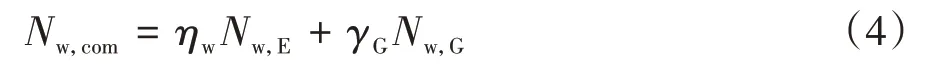
式中：Nw，E為弦桿產生塑性鉸時按圖5所示軸力公式計算的腹桿軸力；Nw，G為重力荷載代表值作用下的腹桿軸力；ηw為腹桿內力設計值增大系數，主要考慮的是弦桿塑性鉸區鋼材強化，可參考現行規范對偏心支撐內力設計值增大系數的規定［14］，根據建筑結構的抗震等級確定；γG為重力荷載分項系數，當重力荷載效應對構件不利時取1.0，重力荷載效應對構件有利時可取小于1.0.

考慮到不同荷載組合下，腹桿內力可能出現大于Nw，com的情況，將Nw，com與按現行規范基于極限狀態法設計的構件內力設計值進行比較，選取更為不利的設計值作為最終設計值進行構件截面設計.

3 層間位移角限值

3.1 彈性層間位移角限值

我國《建筑抗震設計規范》（GB 50011—2010）［13］規定：在多遇地震作用下，建筑主體結構應不受損壞，非結構構件沒有過重破壞并導致人員傷亡，保證建筑的正常使用功能.其中保證建筑的正常使用功能主要包括控制混凝土剪力墻、柱等重要抗側力構件的開裂［15］.對于交錯桁架鋼框架結構而言，混凝土樓板作為豎向承重和水平傳力構件一般按照不出現斜裂縫的深梁設計［9，16］，因此交錯桁架鋼框架結構僅需要通過變形控制非結構構件的損壞即可，參考現行《建筑抗震設計規范》（GB 50011—2010）［13］彈性層間位移角限值可取1/250.

3.2 彈塑性層間位移角限值

結構的整體倒塌或局部倒塌，往往是由于個別主要抗側力構件在強烈地震下的最大變形超過其極限變形能力所造成的，因此，在抗震設計時應進行罕遇地震作用下的結構彈塑性變形驗算.《建筑抗震設計規范》（GB 50011—2010）［13］規定了多種常用鋼結構體系的彈塑性層間位移角限值為1/50，但并不適用于交錯桁架鋼框架結構體系.

根據前述交錯桁架鋼框架結構的設計原則，在罕遇地震作用下結構僅在空腹節間弦桿處出現塑性鉸，其余構件均不發生屈服或保持彈性狀態，所以交錯桁架結構塑性層間位移角僅由空腹節間弦桿塑性變形引起.因此可以將結構在罕遇地震作用下的彈塑性層間位移角分為彈性層間位移角和塑性層間位移角兩部分，即樓層彈塑性層間位移角θ為：

式中：θe為樓層彈性層間位移角；θp為樓層塑性層間位移角.

樓層彈性層間位移角θe根據其組成性質可分為結構整體彈性彎曲變形引起的層間位移角和樓層彈性剪切變形引起的層間位移角，即彈性層間位移角θe為：

式中：θf為結構整體彈性彎曲變形引起層間位移角；θs為樓層彈性剪切層間位移角.我國《建筑抗震設計規范》（GB 50011—2010）［13］指出對于高度大于150 m的結構，計算層間位移角時可以考慮結構整體彎曲變形所產生的影響，而交錯桁架結構目前僅推薦用于100 m及以下結構，故本文計算彈塑性層間位移角限值時偏安全地不考慮交錯桁架結構的整體彎曲變形，即樓層彈性層間位移角為：

樓層彈性剪切位移角θs主要由桁架斜腹桿軸向彈性變形和空腹節間弦桿彈性彎曲變形引起，即樓層彈性剪切位移角θs為：

式中：θs1為桁架斜腹桿軸向彈性變形引起的樓層剪切位移角；θs2為桁架空腹節間弦桿彈性彎曲變形引起的樓層剪切位移角，如圖7 所示，圖中γe為空腹節間弦桿彈性彎曲轉角.

根據圖7，由幾何關系可得斜腹桿軸向彈性變形引起的彈性層間位移角θs1和空腹節間弦桿彎曲彈性變形引起的彈性層間位移角θs2分別為：

圖7 樓層彈性剪切變形Fig.7 Elastic shear deformation of storey

式中：ε為斜腹桿的平均應變；α為斜腹桿與水平面夾角；L為桁架全長；Lv為桁架空腹節間長度.

桁架空腹節間弦桿端部形成塑性鉸時的塑性變形如圖8 所示.根據幾何關系，樓層塑性層間位移角θp為：

圖8 桁架塑性變形圖Fig.8 Plastic deformation diagram of truss

式中：γp為弦桿塑性轉角.

綜合式（5）、式（7）～式（11）可得樓層彈塑性層間位移角θ為：

由式（9）可知，在桁架布置形式確定的情況下，斜腹桿軸向彈性變形引起的樓層剪切位移角θs1的大小取決于斜腹桿平均應變ε的大小.桁架斜腹桿在水平力作用下處于受壓或者受拉狀態，其中斜腹桿受壓時承載力由穩定控制，其彈性極限變形量低于受拉斜腹桿，所以桁架斜腹桿軸向彈性變形引起的樓層剪切位移限值［θs1］取決于受壓斜腹桿的彈性變形能力.規范［9］推薦的斜腹桿截面形式為方鋼管，因此選取幾組斜腹桿常用的方鋼管截面，并根據規范計算其達到受壓承載力設計值時斜腹桿的平均應變ε作為斜腹桿的平均應變限值[ε]，見表3.

由表3可知，不同斜腹桿截面設計平均應變ε介于0.001 0～0.001 2 之間，可偏安全地取0.001 0 作為斜腹桿的平均應變限值[ε].

表3 常用桁架斜腹桿設計平均應變Tab.3 Design average strains of diagonal web member of comon truss

桁架斜腹桿與水平面夾角α一般為30°～60°之間［9］，因此csc2α介于1～1.15 之間，可偏安全地取1作為csc2α的限值，對應桁架斜腹桿與水平面夾角α為45°.

參考ASCE/SEI 41—17［17］中考慮剪切變形的梁屈服轉角的計算方法，空腹節間弦桿彈性彎曲轉角限值[γe]可取為：

式中：As為弦桿腹板面積.

規范［9］推薦的桁架弦桿截面形式為寬翼緣H 型鋼，選取幾組桁架弦桿常用的寬翼緣H 型鋼截面，根據式（13）計算的桁架弦桿屈服轉角見表4.

表4 常用桁架弦桿屈服轉角Tab.4 Yield rotation angles of chord member of comon truss

由表4 可知，常用弦桿截面屈服轉角為0.008～0.010 rad，可偏安全地取0.008 rad作為弦桿彈性彎曲轉角限值[γe].

從式（11）中可看出，在桁架布置形式確定的情況下，空腹節間弦桿的塑性轉動能力越大，樓層可承受的塑性層間位移角也越大，弦桿的延性決定了整個桁架的延性.關于交錯桁架弦桿塑性轉角限值[γp]的試驗研究較少，參考鋼框架梁端塑性轉角的試驗研究［18-23］可知，滿足一定構造措施的鋼梁均能表現出優秀的塑性轉動能力.本文參考美國鋼結構抗震設計規范ANSI/AISC 341—2016［24］中對特殊抗彎框架的規定，取弦桿塑性轉角限值[γp]為0.04 rad.

綜上可知，桁架斜腹桿的平均應變限值[ε]可取0.001，桁架斜腹桿與水平面夾角α取為45°，桁架空腹節間弦桿彈性彎曲轉角限值[γe]可取0.008 rad，弦桿塑性轉角限值[γp]取0.04 rad.根據式（12）可得桁架彈塑性層間位移角限值[θ]為：

以層高3 m，帶斜腹桿節間距均為3 m 的桁架為例，根據式（14）計算出不同空腹節間距的5 節間桁架彈塑性層間位移角限值見表5.

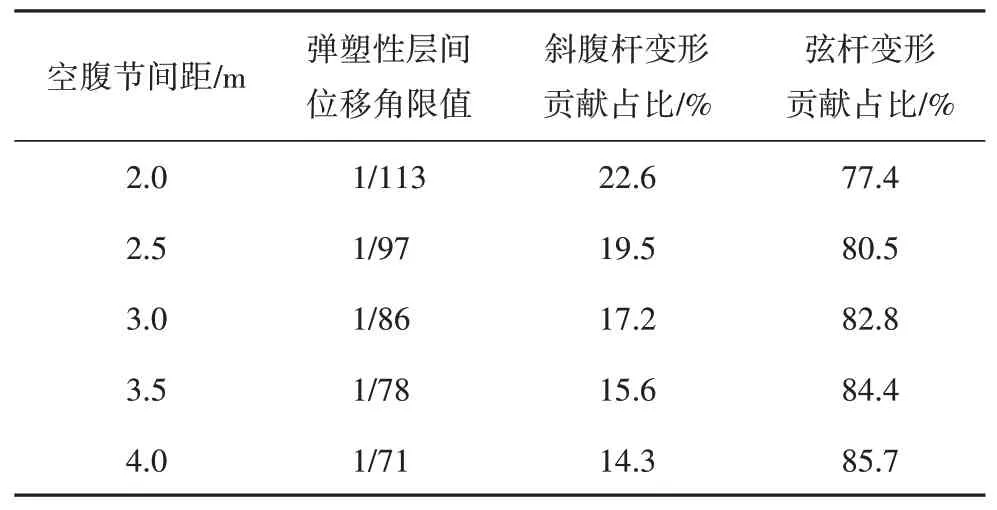
表5 不同空腹節間距結構彈塑性層間位移角限值Tab.5 Limit value of elastoplasticity inter-storey drift ratio under different lengths of vierendeel panels

從式（14）和表5 可知，斜腹桿彈性變形對交錯桁架鋼框架結構彈塑性層間位移角限值的貢獻為0.002 rad；而弦桿彈塑性變形的貢獻隨著空腹節間距與桁架全長比值的增大而增大，且占主要部分；交錯桁架鋼框架結構彈塑性層間位移角限值小于現行《建筑抗震設計規范》（GB 50011—2010）［13］規定的多層和高層鋼結構房屋的彈塑性層間位移角限值（1/50），故交錯桁架鋼框架結構設計時需要根據桁架布置情況選擇相應的彈塑性層間位移角限值.

4 算例分析

4.1 結構設計

基于上述腹桿內力調整方法和彈塑性層間位移角限值規定，提出一種交錯桁架鋼框架結構抗震設計方法，其設計流程見圖9.

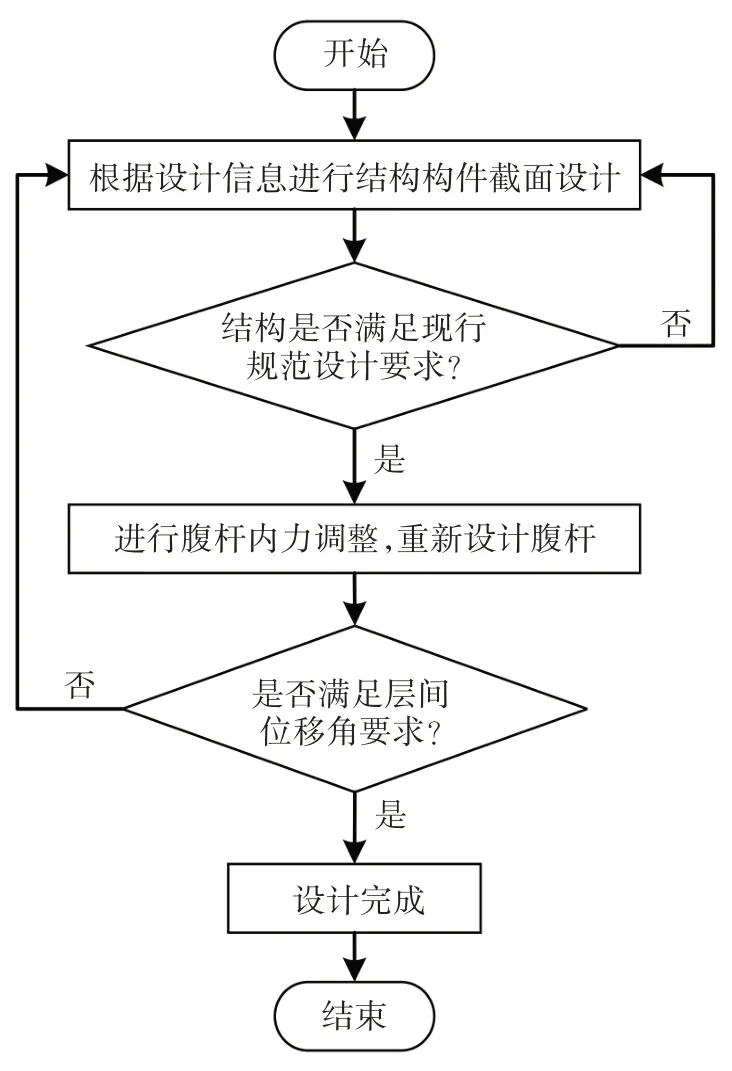
圖9 交錯桁架鋼框架結構抗震設計流程圖Fig.9 Seismic design flow chart of steel staggered truss framing systems

為驗證本文抗震設計方法的合理性，運用結構設計軟件PKPM，按現行規范設計了一棟交錯桁架鋼框架結構SST1，同時按本文提出的抗震設計方法設計了一棟交錯桁架鋼框架結構SST2.結構布置如圖10 和圖11 所示，荷載信息為：樓屋面恒載（含樓板自重）為5 kN/m2，樓屋面活載為2 kN/m2，抗震設防烈度為8 度（0.2g），設計地震分組為第二組，場地類別為Ⅱ類.

圖10 結構平面布置圖Fig.10 Structural plan

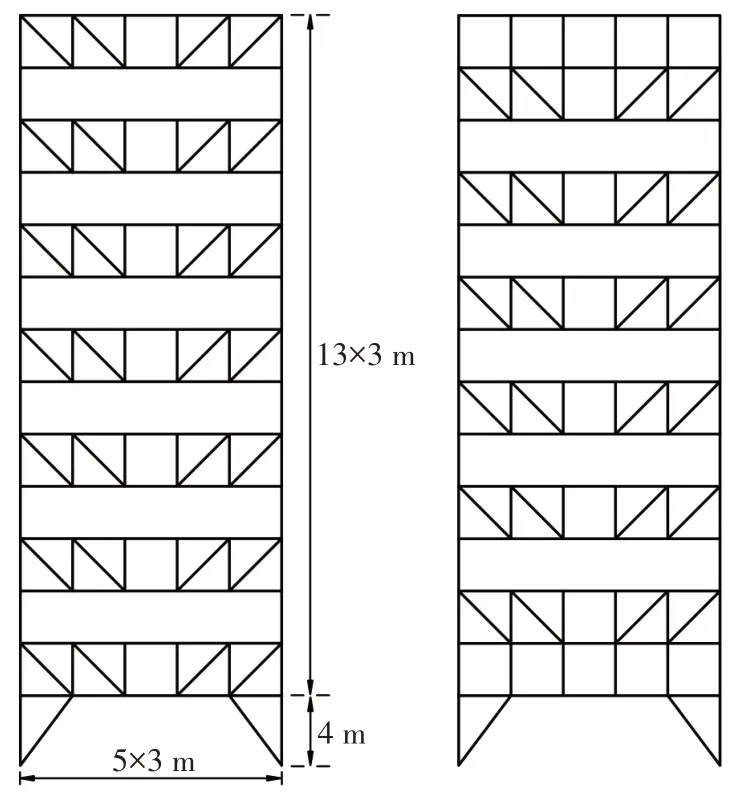
圖11 結構立面圖Fig.11 Structural elevation

SST1 和SST2 構件截面尺寸見表6.SST1 和SST2的鋼柱、底層支撐、弦桿截面尺寸相同，腹桿截面尺寸不同，鋼材選用Q345，混凝土樓板厚度均為120 mm，混凝土強度均為C30.其中，SST2 腹桿內力調整時，腹桿內力設計值增大系數ηw取為1.3；計算弦桿塑性鉸彎矩Mp時，弦桿-樓板組合效應的放大系數取為1.5.

表6 結構構件截面尺寸Tab.6 Sections and dimensions of structural members

4.2 罕遇地震下結構彈塑性時程分析

為了評估所設計的模型SST1 和SST2 的抗震性能，運用有限元軟件SAP2000 對其分別進行了彈塑性時程分析，其中結構阻尼比取值為0.05，根據2.2節分析，模型中弦桿剛度放大系數取為1.5.

4.2.1 地震波的選取

根據我國抗震規范及有關研究的建議［13，25］，地震波的選取需滿足地震動幅值、持時和頻譜特性的要求，即8 度（0.2g）罕遇地震波峰值加速度（Peek Ground Acceleration，PGA）取400 gal；地震動有效持時需大于結構基本周期的5 倍；地震記錄反應譜與規范反應譜在平臺段和結構基本周期附近均值相差不超過10%.模型SST1和SST2計算所得的橫向基本自振周期分別為1.84 s 和1.73 s，從太平洋地震工程研究中心數據庫（PEER ground motion database）中篩選出地震動有效持時（D5-95）大于9.2 s 的地震動記錄，根據頻譜特征選擇10 條地震波并將每條地震波PGA 縮放到400 gal，所選地震波信息及頻譜特性如表7和圖12所示.

圖12 地震波反應譜Fig.12 Response spectrum of seismic records

表7 地震波信息Tab.7 Information of seismic records

4.2.2 構件損傷狀態及性能水準定義

SAP2000 采用集中塑性鉸模型表征構件的彈塑性性能及損傷狀態，塑性鉸為鋼塑性，無彈性行為，桿件其余部分保持彈性.算例中的柱采用P-M2-M3鉸，桁架弦桿采用彎曲鉸，桁架腹桿采用軸力鉸，并在動力時程分析時采用程序默認的等向強化滯回準則.圖13為彎曲鉸非線性力-變形關系示意圖.

圖13 彎曲鉸非線性力-變形關系曲線Fig.13 Nonlinear force-displacement relationship of moment hinge

圖13 中，B 為屈服點；C 為破壞點，即構件達到承載力極限狀態；D為倒塌點；E為最大變形點.基于構件內力與宏觀變形關系，構件性能水準包含立即使用（IO）、生命安全（LS）、接近倒塌（CP）三個性能點.

塑性鉸參數及各性能目標對應的變形限值大小取決于構件截面寬厚比和柱軸力等因素，參照ASCE/SEI 41—17［17］中表9-6、表9-7 所推薦的數值，本算例中弦桿性能目標與變形值的對應關系見表8.

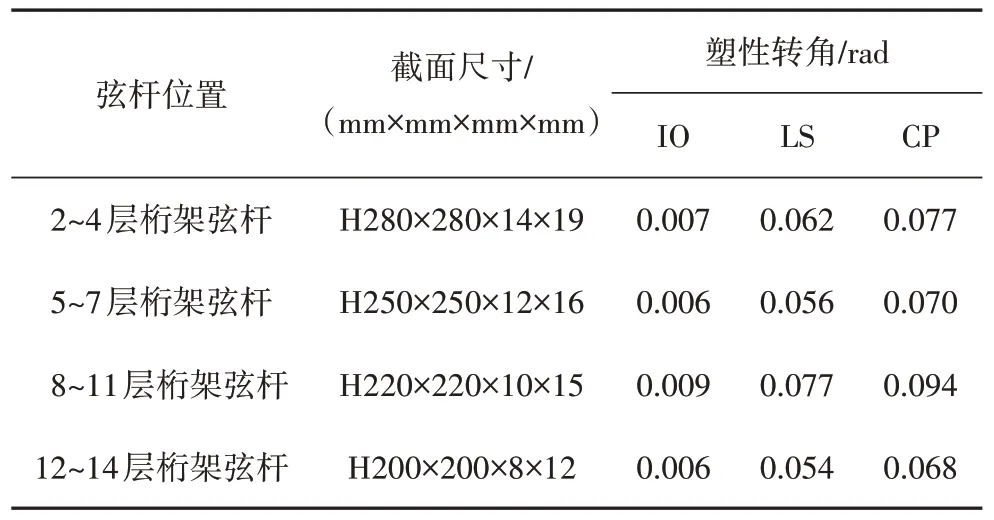
表8 弦桿各性能水準塑性轉角Tab.8 Plastic rotation of chord member under different performance levels

4.2.3 地震響應分析結果

通過對模型SST1和SST2進行8度（0.2g）罕遇地震下的彈塑性時程分析，在地震波GM2 作用下結構的損傷最為嚴重，限于篇幅，本文僅以地震波GM2波作用下的結構響應為例進行對比分析.GM2 波作用下結構頂點位移-時程曲線，如圖14所示.

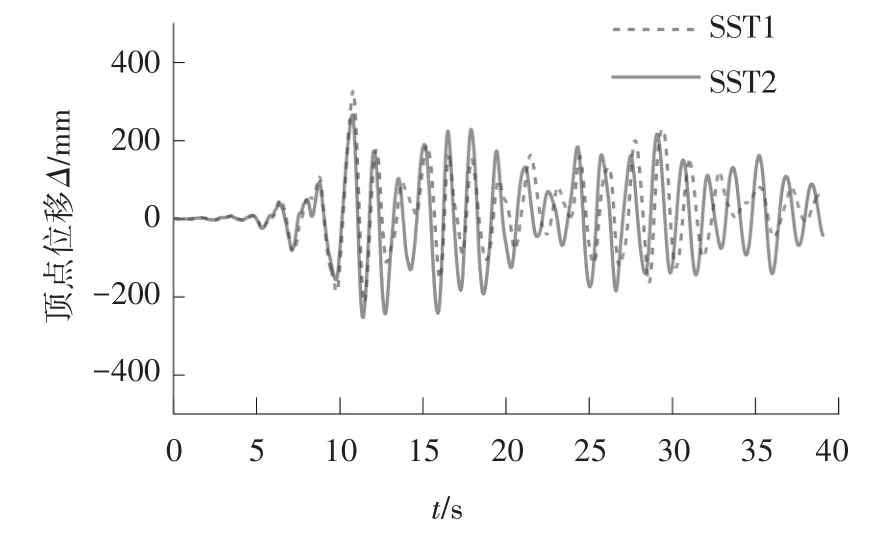
圖14 頂點位移-時程曲線Fig.14 Time history curve of roof displacement

從圖14可知，SST1模型最大頂點位移大于SST2模型.SST2 模型頂點最大位移出現在10.76 s 時，為265 mm.此時，結構整體變形近似于結構在桁架向的一階振型，桁架兩側柱頂點高差為20 mm，計算可得此時結構整體彎曲引起的頂層層間位移角θf14為0.001 3 rad.由于θf隨著樓層高度增加而增大，即其他樓層θf均小于0.001 3 rad，遠小于樓層總體層間位移角，可忽略結構整體彎曲對層間位移角的貢獻，說明此算例結構變形模式屬剪切型，也證明了上文提到的“結構整體彎曲變形對層間位移影響相對較小”的結論.

圖15 給出了彈塑性時程分析得出的樓層最大層間位移角包絡曲線，SST2 模型各層層間位移角分布較為均勻，無明顯薄弱層，最大層間位移角出現在第9 層，為1/94，小于上節所得到的限值要求（1/86），結構底層由于并未布置桁架，其層間位移角限值可按照鋼框架結構控制（1/50）.SST1 模型最大層間位移角出現在第2 層，為1/74，底部樓層層間位移角顯著大于中上部樓層，這是由于2 層、3 層部分桁架斜腹桿在罕遇地震下產生嚴重損傷，導致了樓層抗側剛度發生嚴重退化，形成薄弱層.

圖15 層間位移角包絡曲線Fig.15 Envelope curve of inter-storey drift ratio

SST1 和SST2 結構典型榀塑性鉸分布情況如圖16～17 所示.從圖16 中可知基于傳統極限狀態法設計的SST1 結構由于未經設計內力調整，其部分斜腹桿出現塑性鉸，且2～3 層部分斜腹桿由于變形過大已經發生嚴重損傷，超出CP（接近倒塌）性能點，結構難以保證“大震不倒”的設計目標；而圖17 中按照本文所述方法設計的SST2結構在罕遇地震作用下，斜腹桿始終處于彈性狀態，弦桿塑性鉸發展充分，能夠較為良好地耗散地震能量，結構整體可以實現“大震不倒”的設計目標.

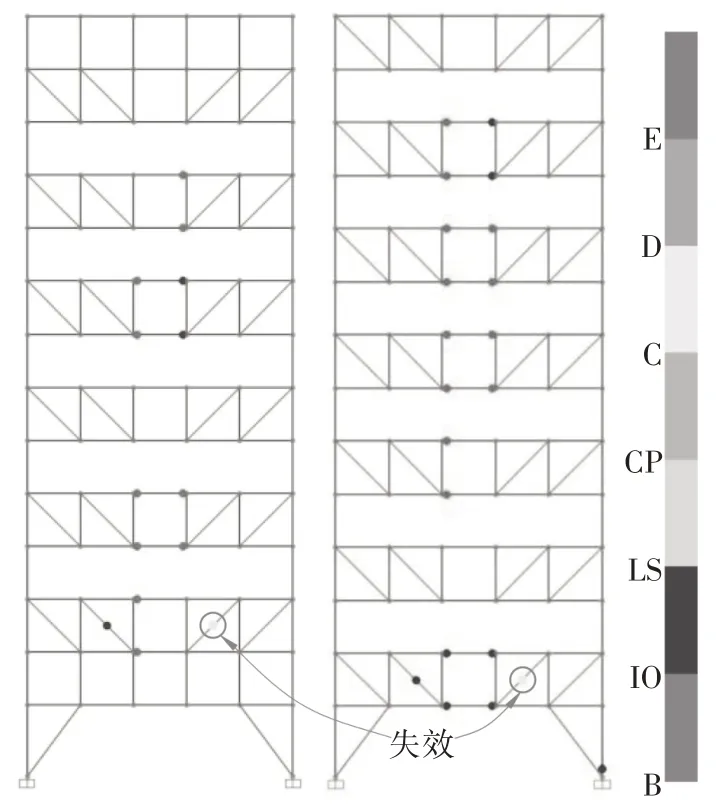
圖16 SST1典型榀最終塑性鉸分布Fig.16 Plastic hinge formation in SST1

圖17 SST2典型榀最終塑性鉸分布Fig.17 Plastic hinge formation in SST2

5 結論

1）基于桁架空腹節間弦桿破壞的結構失效模式，提出了水平力作用下桁架桿件內力計算模型及罕遇地震作用下桁架腹桿內力的調整方法.

2）基于桁架弦桿失效的結構失效模式和桁架的極限變形，提出了不同空腹節間距下結構的彈塑性層間位移角限值.

3）提出了一種交錯桁架鋼框架結構抗震設計方法及流程.算例分析表明，采用本文方法設計的交錯桁架鋼框架結構能有效耗散地震能量，實現“強腹桿弱弦桿”和“大震不倒”的設計目標.