鋼框架結構離散優化問題的理論下界

王興鋒，張氫，秦仙蓉，孫遠韜

（同濟大學機械與能源工程學院，上海 201804）

在鋼框架結構的設計中，結構的桿件一般從標準型鋼庫中選取，通過組合得到滿足性能要求的最佳設計方案，因此，鋼框架結構的優化設計是一個典型的離散優化問題.

當前對鋼框架結構離散優化問題的研究，幾乎都側重于提出新的優化方法，以期獲得滿足工程精度要求的近似最優解.這些優化方法覆蓋了元啟發式算法［1-5］、優化準則法［6-7］、基于梯度的數學規劃方法［8-9］，但幾乎沒有研究能夠針對特定類型的鋼框架結構離散優化問題，明確指出優化方法的求解結果與全局最優解的距離.為確定優化算法的求解精度，一般做法是通過與多種優化方法的結果進行對比.這種論證方法只能粗略地說明優化算法的求解精度，而且需要廣泛地、有代表性地選取作為對比的優化算法.為證明某種優化算法的求解精度，一種更直接的方法是，獲取優化問題的全局最優解，或者優化問題的理論下限（假設優化問題為最小化問題）.盡管在工程實際問題中，由于約束的復雜性，幾乎不可能得到優化問題的全局最優解，但針對特定類型的鋼框架結構離散優化問題，還是有可能獲得全局最優解或理論下界.

在這方面，已經有少數學者展開了研究.針對含應力和位移約束、以體積最小為目標的鋼框架結構離散優化問題，Van 等［10］提出了一種優化方法，通過將原優化問題建模為混合整數優化問題，從而得到離散優化問題的全局最優解.針對含體積約束、以柔度最小為目標的鋼框架結構離散拓撲-尺寸優化問題，Kanno［11］提出了一種混合整數二階錐規劃的建模方法，將原優化問題轉化為一個凸規劃問題，從而也得到了原問題的全局最優.kureta 等［12］針對負泊松比的周期性框架結構的離散優化問題，提出了一種混合整數的線性規劃方法.Hirota等［13］將混合整數的線性規劃建模方法，進一步推廣到具有負熱膨脹能力的周期性框架結構的離散拓撲優化中.

在鋼框架結構中，桿件的截面參數包括截面寬度、高度、板厚，以及截面面積、強弱軸慣性矩等.對于標準型鋼截面，這些截面參數是相互關聯的，選定某一個截面參數則意味著同一截面的其他參數也被選中，故稱為關聯離散變量［14-15］.在以上研究中［10-13］，關聯離散變量是通過0-1 變量進行定義，以此來表征是否選擇了某個標準截面，對應的優化問題都是含0-1 變量的凸規劃問題.對于此類優化問題，一般采用隱枚舉法（如分支定界法）進行求解，計算效率非常低，若結構中的桿件數量或可選的標準截面增多，計算效率會大幅下降.

有鑒于此，本文提出了一種新的離散變量處理方法，即基于凸組合的線性松弛方法.該方法將關聯離散變量進行線性松弛，從而將結構的剛度矩陣轉化為設計變量的線性函數，根據這一優勢，可以將鋼框架結構離散優化中的多種非線性優化問題進一步建模為凸規劃問題.本文重點分析了兩類非線性優化問題：柔度約束的最小體積問題和體積約束的最小柔度問題.根據剛度矩陣與設計變量的線性關系，將柔度約束的最小體積問題轉化為半定規劃問題，將體積約束的最小柔度問題轉化為二階錐規劃問題.采用現成的優化求解器，直接求解這兩類凸規劃問題，快速得到松弛問題的全局最優解，也就是離散優化問題的理論下界.

1 離散變量的定義方法

在鋼框架結構的離散優化設計中，桿件截面從標準型鋼庫中選取：

式中：S為標準截面構成的集合；為標準型鋼的截面參數；p為標準型鋼的個數.

對于關聯離散變量，一種常見的處理方法為采用0-1變量：

式中：ti為0-1 變量，用于表征某一標準截面是否被選中.這種定義方法的本質，是在p維的0-1 離散空間與標準截面集S之間定義了一種映射關系.

若優化數學模型中包含0-1 變量，則求解特別耗時，為此，本文提出了一種新的離散變量定義方法，即基于凸組合的線性松弛方法.

對于平面鋼框架結構的優化問題，若只考慮結構的軸向變形和彎曲變形，則結構的剛度矩陣僅僅與桿件的截面面積和慣性矩有關.因此，在作者前期的研究［16］中，提出了以截面面積和慣性矩為設計變量的定義方法：

式中：A、I分別為桿件的截面面積和慣性矩.考慮到標準型鋼的A和I是關聯離散變量，優化過程中需要同時選取某一標準截面的A和I，故在每一次優化迭代后將設計變量圓整到標準截面.根據式（5），標準型鋼可視為二維空間中的一個離散點（見圖1）.

圖1 基于凸組合的線性松弛Fig.1 Linear relaxation based on convex combination

對于空間中的任意多個點，總是存在一個包含所有點的最小凸多邊形（即凸包），使得凸多邊形內的任意一點，都可以用凸多邊形頂點的凸組合進行描述.因此，提出一種基于凸組合的線性松弛方法，將式（5）表示的變量定義方法推廣到連續空間：

在式（6）～（9）中，將基于凸多邊形的線性松弛方法應用于二維空間，若將這一方法應用于一維空間時，就退化為一種常見的松弛方法.以桁架結構的離散優化問題為例，假設桿件的可選截面集為：

式中：c1、c2為凸組合系數.顯然，式（12）～（14）就是式（6）～（9）的一維形式.

根據式（6）～（9），離散優化問題的設計變量變成連續松弛變量（即凸組合系數），而標準截面的截面面積和慣性矩成為設計變量的線性函數.由此，鋼框架結構的剛度矩陣成為凸組合系數的線性函數.根據這一特性，可以將兩類典型的鋼框架結構離散優化問題，即柔度約束的最小體積問題、體積約束的最小柔度問題，分別轉化為松弛的凸規劃問題.

2 凸規劃建模

2.1 柔度約束的最小體積問題

在鋼框架結構的離散優化中，柔度約束的最小體積問題可表達如下：

式中：Li、Ai分別為第i個桿件的長度和截面面積；n為桿件的總數；K為結構的剛度矩陣；U為節點位移列陣；F為載荷列陣；為柔度上限.

根據桁架結構的研究［17-18］，桁架結構的柔度約束和力平衡約束可等效于矩陣的半正定約束：

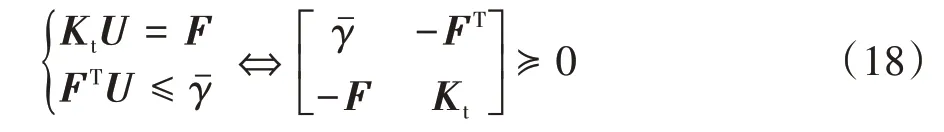
式中：Kt為桁架結構的剛度矩陣.

式（18）成立的一個重要前提條件，就是Kt為桿件截面面積的線性函數.根據本文提出的線性松弛方法，鋼框架結構的剛度矩陣也成為設計變量的線性函數，故同樣可以將鋼框架結構的柔度約束最小體積問題轉化為半定規劃問題：

式中：K(C)為鋼框架結構的剛度矩陣；C為凸組合系數矩陣.

針對半定規劃問題，當前已經有多個成熟的優化求解器，如MOSEK［19］、SeDuMi［20］.應用這些求解器，可以快速得到半定規劃問題的全局最優解，也就是離散優化問題的理論下界.

2.2 體積約束的最小柔度問題

在鋼框架結構的離散優化中，體積約束的最小柔度問題可表達如下：

根據Kanno［11］，體積約束的最小柔度問題可轉化為混合整數的二階錐規劃問題：

式中：wil(l=1，2，3)是桿件i的應變余能；sil(l=1，2，3)是桿件i的內力；bil(l=1，2，3)為桿件i的方向列陣，具體計算方法可參照文獻［11］的附錄A.

其中，Ai、Ii屬于關聯離散變量，Kanno［11］采用0-1變量的定義方法進行處理.為提高問題的求解效率，快速得到離散優化問題的理論下界，本文采用基于凸組合的線性松弛方法來重新定義離散變量：

式（33）～（36）僅包含線性約束，不改變優化問題的數學特性，故所得到的優化問題仍然屬于二階錐規劃問題.二階錐規劃問題可以用成熟的優化求解器（如MOSEK、CPLEX［21］、Gurobi［22］或SeDuMi）進行快速求解，進而得到原離散優化問題的理論下界.

3 數值算例

通過求解一跨四層鋼框架結構的離散優化問題，對所提出的方法進行驗證.鋼框架結構的尺寸、桿件分組和加載情況如圖2所示.桿件的彈性模量為2.1×105MPa，體積上限為0.18 m3，柔度上限為25.結構中的桿件從標準規格中的H 型鋼［23］中選取（見表1），H型鋼在二維空間中的分布如圖1所示.

圖2 一跨四層鋼框架Fig.2 One-bay-four-story steel frame

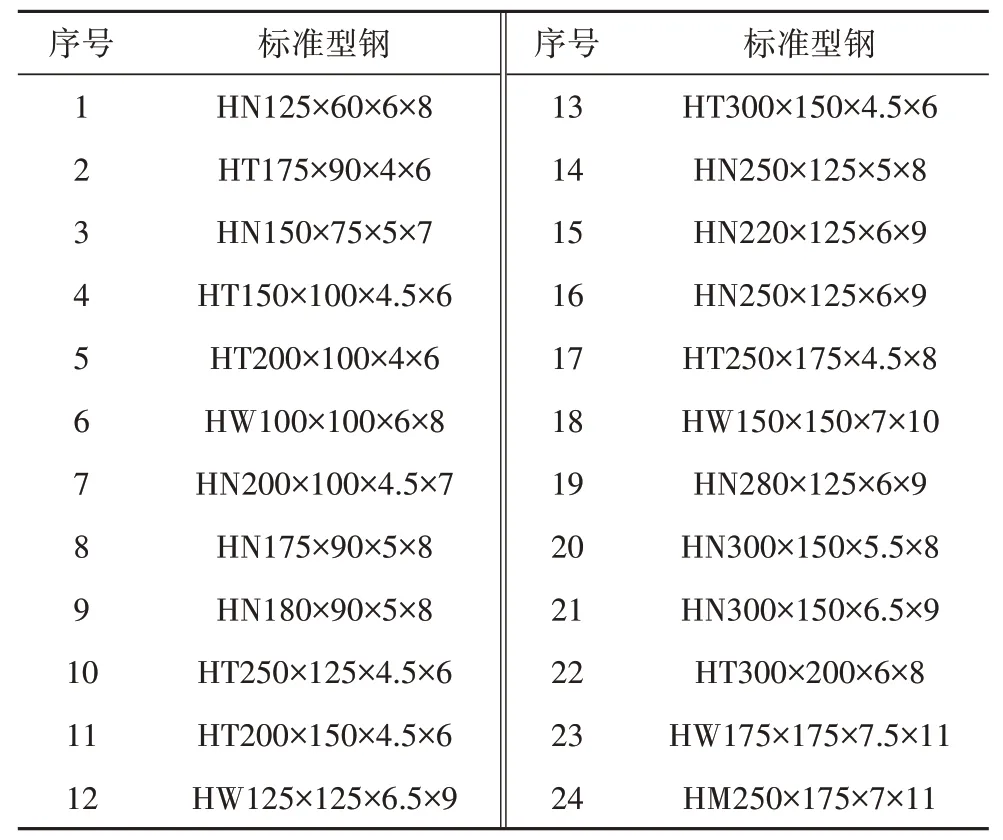
表1 H型鋼Tab.1 H-shaped standard sections

采用枚舉法計算離散優化問題的全局最優解，并驗證所提出方法求解優化問題的理論下界的能力.為判斷所提出方法的計算效率，再用遺傳算法（Genetic Algorithm，GA）求解當前優化問題.GA是一種經典的智能優化算法，可依概率收斂到優化問題的全局最優解，因此采用GA 與所提出方法進行對比.采用MATLAB 平臺自帶的ga 求解器作為GA 的實現，其中：種群大小為30，最大迭代次數為500，其余參數都采用默認值.將GA 獨立運行30 次，得到最佳的優化結果.

為了對關聯離散變量進行線性松弛，需要定義包含離散點集的凸包.對于平面內的離散點集，可采用經典的Graham掃描算法［24］獲得對應的凸包.

所有的優化計算都在MATLAB 平臺中編碼，并在一臺工作站中執行.該工作站含雙核2.2.GHz Xeon處理器，運行內存為32 GB.

3.1 柔度約束的最小體積問題

采用MOSEK 求解松弛的半定規劃問題，得到松弛最優解.采用枚舉法求解該離散優化問題，得到離散的全局最優解，并采用GA 得到近似最優解.松弛最優解對應的結構體積為0.137 8 m3，結構柔度為25.00；離散全局最優解對應的結構體積為0.141 4 m3，結構柔度為24.96；GA 得到的近似最優解對應的結構體積為0.142 0 m3，結構柔度為24.75.顯然，松弛最優解比離散全局最優解略小，松弛最優解成為了離散優化問題的理論下界.同時，根據松弛最優解進行鄰域搜索，可以快速得到高質量的離散可行解，甚至是離散的全局最優解.

基于半定規劃的方法僅需要采用調用一次優化求解器、耗時0.51 s，就可以得到優化問題的理論下界，而枚舉法需要求解524（≈5.96×1016）個子問題、耗時1 724.21 s，才能得到離散的全局最優解.為了得到近似最優解，GA 需要獨立運行多次，而每一次運行的計算時間都超過1 s（介于1.10 s到2.00 s之間），所以，GA 的計算效率也遠不如所提出的半定規劃方法.顯然，當需要判斷某種算法的優化結果是否為全局最優時，半規劃方法可以是一種高效的驗證方法，尤其是對于規模稍大一些的同類優化問題.

松弛最優解和離散最優解在空間中的分布情況如圖3所示，離散最優解如表2所示.

圖3 柔度約束問題最優解的分布情況Fig.3 Distribution of optimum solution for compliance-constrained problem

表2 柔度約束問題的離散最優解Tab.2 Optimum solution for compliance-constrained problem

3.2 體積約束的最小柔度問題

采用MOSEK 求解松弛的二階錐規劃問題，同時采用枚舉法求解離散優化問題的全局最優解，并采用GA 得到近似最優解.優化結果如下：松弛最優解的最小柔度為17.74，結構體積為0.180 0 m3；離散全局最優解的最小柔度為18.09，結構體積為0.179 0 m3；GA 得到的近似最優解對應的結構柔度為18.00，結構體積為0.180 1 m3，略大于體積上限.因此，對于體積約束的最小柔度離散優化問題，采用二階錐規劃的方法也可以得到離散問題的理論下界.可以根據松弛最優解進行鄰域搜索，得到離散優化問題的可行解.

同樣的，基于二階錐規劃方法僅調用一次優化求解器、耗時0.67 s，就能夠得到離散優化問題的理論下界，而采用枚舉法需要計算524（≈5.96×1016）個子問題、耗時1 605.13 s，才能得到離散的全局最優解.為了得到近似最優解，GA 需要運行多次，而每一次運行的計算時間都超過0.70 s（介于0.70 s 到1.50 s之間），所以，二階錐規劃方法的計算效率遠高于枚舉法和GA.

松弛最優解和離散全局最優解在空間中的分布情況如圖4所示，離散最優解如表3所示.

表3 體積約束問題的離散最優解Tab.3 Optimum solution for volume-constrained problem

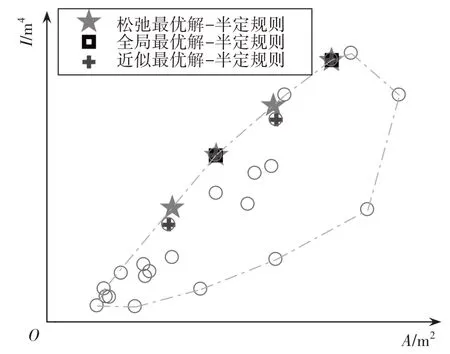
圖4 體積約束問題最優解的分布情況Fig.4 Distribution of optimum solution for volume-constrained problem

4 結論

針對兩類典型的鋼框架結構離散優化問題，即柔度約束的最小體積問題、體積約束的最小柔度問題，進行了研究并得到如下結論：

1）基于凸組合的線性松弛方法，可以實現離散設計變量的線性松弛，使結構的剛度矩陣成為設計變量的線性函數，從而可將柔度約束的最小體積問題轉化為松弛的半定規劃問題，將體積約束的最小柔度問題轉化為松弛的二階錐規劃問題.對這兩類松弛的凸規劃問題，可以快速得到全局最優解，即離散優化問題的理論下界.

2）基于松弛的半定規劃方法和二階錐規劃方法，可以高效求解柔度約束的最小體積問題、體積約束的最小柔度問題，且求解效率遠高于枚舉法.因此，采用松弛的半定規劃方法和二階錐規劃方法，可以快速驗證某種優化方法是否得到全局最優解.

需要說明的是，基于凸組合的線性松弛方法實現了桿件的截面面積和慣性矩的線性化描述，但未能對其他截面屬性進行線性化描述.因此，本文的優化方法適用于僅考慮桿件的拉壓變形和彎曲變形的平面鋼框架結構.