頻相失配下跳頻保密通信性能分析與功率優化
宋長慶,趙宏志,秦儷之,邵士海
(1.電子科技大學通信抗干擾技術國家級重點實驗室,四川 成都 611731;2.電磁空間認知與智能控制技術實驗室,北京 100089)
0 引言
隨著通信網絡的不斷升級,人-人通信、人-機交互、萬物互聯高速發展[1],促使無線連接數量迅猛增長[2]。然而,大量的瞬時連接會造成頻譜資源的擁堵與混亂,非預期的帶外串擾與帶內干擾極大降低了通信服務質量[3]。與此同時,通信用戶對保密性能的關注度不斷提升[4],但無線信道的開放性使大量保密信息存在被非法竊聽的風險[5]。人工噪聲掩護的跳頻保密架構中[6],收發信機間利用跳頻技術躲避電磁干擾,并采用人工噪聲構造與抑制技術阻塞非法竊聽,有效提升了通信系統的保密性能。
理想情況下,保密架構中人工噪聲可以在合法接收機處被完美抑制。然而收發信機在寬帶范圍內持續、快速跳變載波頻率會引起嚴重的收發頻率、相位失配問題,導致系統的人工噪聲抑制能力下降。一方面,載波頻率的快速跳變[7]和多普勒效應[8]會導致收發載波頻率難以精準對齊,收發信機間不可避免地存在頻率偏移[9],這會在人工噪聲抑制步驟中引起頻率間干擾,進而降低接收機處人工噪聲的抑制效果[10]。另一方面,收發頻率振蕩器處熱噪聲會在載波信號中引入相位噪聲[11],導致信號頻譜展寬并引入載波間干擾,進而降低系統的人工噪聲抑制與保密性能[12]。針對頻相失配問題,文獻[13]提出具有頻率偏移穩健性的發射功率優化方案;文獻[14]提出具有相位噪聲穩健性的鎖相環頻率振蕩器優化方案;文獻[15]根據相位噪聲水平,從系統設計角度宏觀協調收發信機參數,進而降低由相位噪聲引起的性能損失。然而上述研究僅適用于定頻通信系統,且僅針對單一頻相失配因素進行系統優化,所得結論并不適用于載頻快速跳變的跳頻通信系統。即在頻相失配問題嚴重的跳頻系統中,接收機處人工噪聲抑制能力與系統保密性能無法得到有效保證。
鑒于此,本文對頻相失配下跳頻收發信號進行數學建模,利用信噪比指標衡量接收機處人工噪聲抑制能力,并利用保密容量指標衡量跳頻系統的保密性能。在此基礎上,給出了具有頻相誤差穩健性的發射功率分配方案,并根據不同的頻相匹配度與傳播信道質量對所提方案進行了簡化與拓展,有效降低了由頻相失配引起的系統性能損失。
1 通信系統模型
本文采用的跳頻保密系統模型與無線通信環境如圖1 所示。由于無線信道的開放性,收發信機正常通信時一方面容易遭受電磁干擾的侵襲,導致接收信號質量下降、數字基帶接收信號處理性能降低;另一方面,隨著竊聽設備的硬件升級與信號處理能力的大幅提升,保密信號更容易遭受非法捕獲,增大了保密通信信息被非法竊聽的風險。面對日益惡劣的電磁通信環境,本文中收發信機間采用跳頻技術躲避惡意干擾[16],并采用人工噪聲構造與抑制技術阻塞非法竊聽[17]。
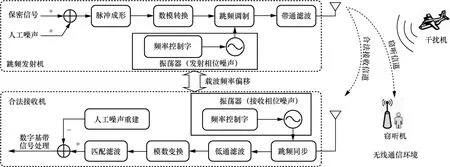
圖1 跳頻保密系統模型與無線通信環境
1.1 跳頻發射機
在跳頻發射機處,保密信號與人工噪聲的和信號依次經過脈沖成形、數模變換、跳頻調制、帶通濾波后發送,其中脈沖成形步驟采用了根升余弦滾降濾波器。保密信號和人工噪聲分別記為x(t) 和z(t),兩者相互獨立。跳頻發射信號可以表示為
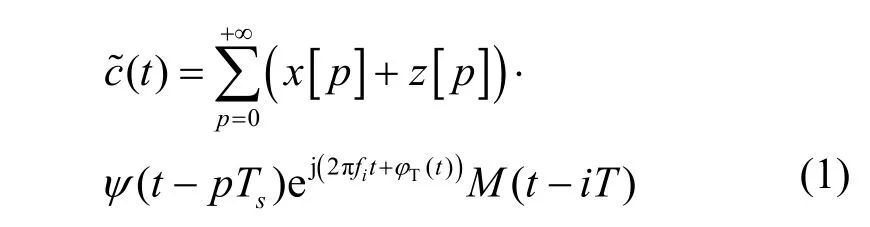
其中,ψ(t) 為根升余弦滾降濾波器的沖激響應[18];fi為第i跳發射信號的中心頻率,i為非負整數;為發射機處的相位噪聲[19];T=NTs為每跳信號的周期,N為每跳包含的符號數,Ts為每個符號的有效時間;x[p]和z[p]分別為保密信號x(t) 和人工噪聲z(t)的第p個符號,p為非負整數;M(t)為每跳有效時間的矩形窗函數,當t∈(0,T]時取值為1,否則為0。
1.2 合法接收機
假設合法收發信機間的傳播信道為平坦慢衰落信道[17],合法接收機處射頻接收信號為
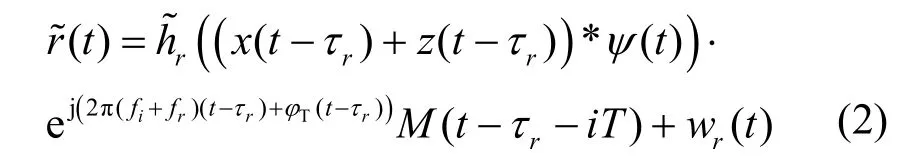
首先,合法接收機依次對接收信號執行跳頻同步、低通濾波、模數變換、匹配濾波操作,將跳頻接收信號解跳到基帶實現跳頻同步。所得數字基帶接收信號可以表示為
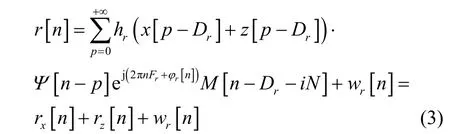
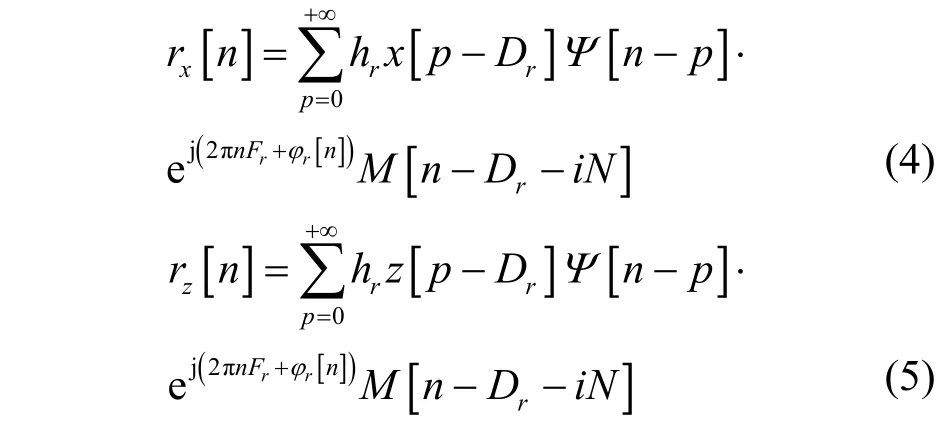
其中,rx[n]、rz[n]與wr[n]分別為保密信號成分、人工噪聲成分和高斯白噪聲成分。
接著,合法接收機執行人工噪聲重構與抑制步驟[17]。記合法接收機重構的人工噪聲序列為從r[n]中減去即可完成人工噪聲抑制,所得信號 Δr[n]滿足
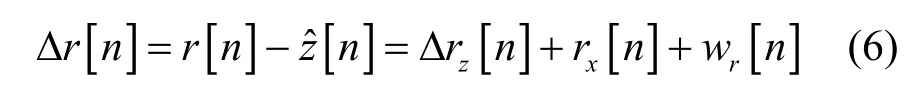
1.3 竊聽機
假設發射機與竊聽機間的傳播信道為平坦慢衰落信道[17],竊聽機處射頻接收信號為
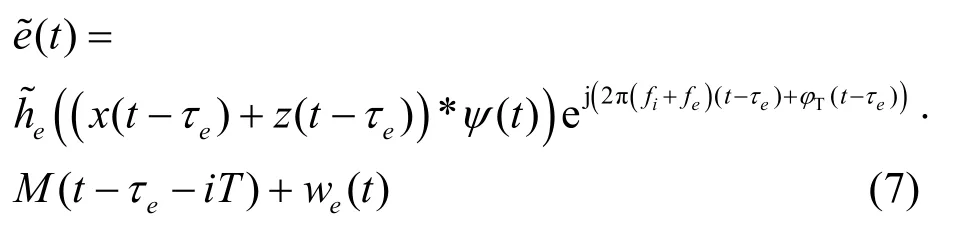
在強竊聽場景下[20],竊聽機可以完美執行跳頻同步、模數變換、匹配濾波步驟。與式(3)相似,竊聽機處數字基帶接收信號可以表示為

由式(8)可以發現,竊聽機將接收跳頻信號解跳后,所得數字基帶信號仍包含人工噪聲成分。由于缺乏人工噪聲先驗信息,竊聽機無法執行人工噪聲重構與抑制步驟,使e[n] 的信噪比遠低于解調門限,因此無法完成保密信號的有效竊取。
2 頻相失配下跳頻系統性能分析
理想情況下,合法接收機可以完美抑制接收信號中的人工噪聲成分。然而跳頻收發頻率振蕩器處存在頻相失配問題,會引起顯著的人工噪聲抑制性能下降與系統保密性能損失,本節將給出具體的性能分析。
2.1 人工噪聲抑制性能
在人工噪聲抑制前,合法接收機先估計接收信號的傳播信道信息。記歸一化傳播時延、歸一化頻率偏移、等效信道增益的估計值分別為為了分離出頻相失配對人工噪聲抑制性能的影響,假設合法接收機處的傳播時延被完美估計,即此外表示收發頻率振蕩器間的歸一化載波頻率偏移,頻偏估計值每跳更新一次,即更新周期為N個符號。
完成信道參數估計后,合法接收機對本地預存的人工噪聲序列z[n] 進行時間對齊、頻率偏移補償、脈沖成形,其中脈沖成形采用沖激響應為Ψ[n]的升余弦滾降濾波器。記補償后得到的序列為表達式為


經過人工噪聲抑制后,記殘余人工噪聲為Δrz[n],其頻域表達式ΔRz[k]滿足
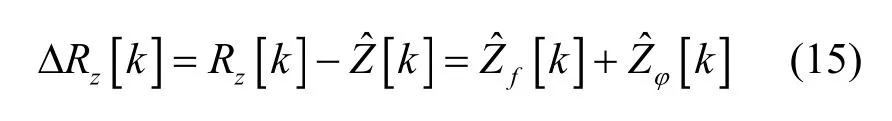
接下來,計算接收信號中各成分的功率。記發射機功率預算為P=Px+Pz,其中,Px和Pz分別表示保密信號和人工噪聲的發射功率。記 P {·}表示求取{·} 的功率,則ΔRz[k]的功率為

命題1在圖1 所示的跳頻保密系統模型中,相位噪聲水平對人工噪聲抑制性能的影響程度可以用衡量[21],λ取值越大,相位噪聲的負面影響越小。此外,λ與信道估計周期N和3 dB相干帶寬有關,并有如下特征。
1)λ關于N的一階偏導恒小于零,表明λ隨N的減小而增大。特別地,本文有如下結論。①當N趨于1 時,λ滿足此時接收機可以完美消除相位噪聲的影響。
② 當N趨于無窮大時,λ滿足,表明如果不及時更新信道估計值,由相位噪聲引起的人工噪聲抑制性能惡化將不斷加劇。
2)λ關于的一階偏導恒小于零,表明λ隨的減小而增大。特別地,本文有如下結論。
記合法接收機處信噪比為SANNRr,其中噪聲包括熱噪聲和人工噪聲成分。由式(16)~式(17)可知,當存在頻相失配時,合法接收機處SANNRr的表達式為
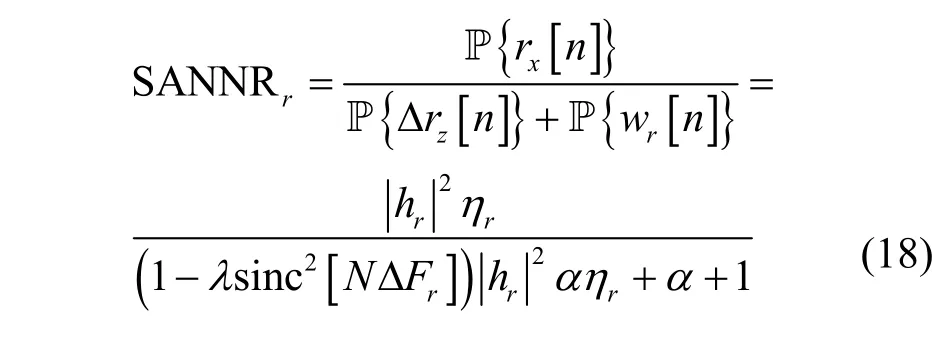
命題2在圖1 所示的跳頻保密系統模型中,合法接收機處人工噪聲抑制效果可以用SANNRr指標來衡量[17],其表達式如式(18)所示。可以發現,SANNRr與頻率偏移、相位噪聲水平、信道估計周期N、發射機與合法接收機間的主信道質量有關,并有如下特征。
1) 隨著歸一化頻率偏移ΔFr的增大,SANNRr整體呈下降趨勢。特別地,本文有如下結論。
①當ΔFr趨于0 時,SANNRr滿足
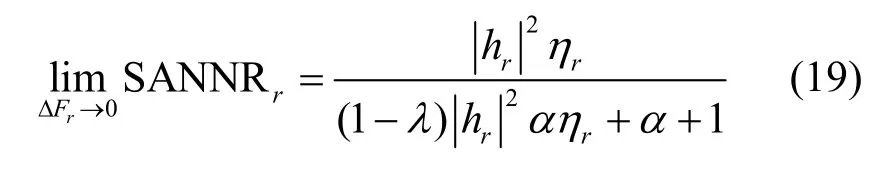
式(19)表征了合法接收機實現完美頻率同步時的人工噪聲抑制性能,此時,SANNRr與主信道質量、功率分配因子、信道估計周期、3 dB 相干帶寬有關。
② 隨著ΔFr的不斷增大,當時,SANNRr滿足
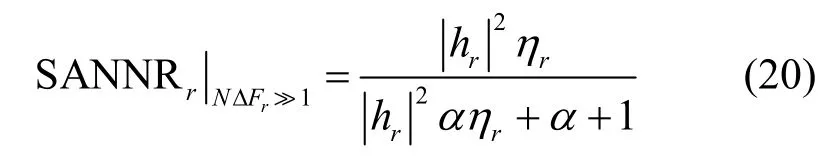
此時,SANNRr僅與主信道質量、功率分配因子α、信道估計周期有關,相位噪聲對人工噪聲抑制性能的影響可以被忽略。
2) SANNRr隨著相位噪聲水平的抬升而減小。特別地,本文有如下結論。
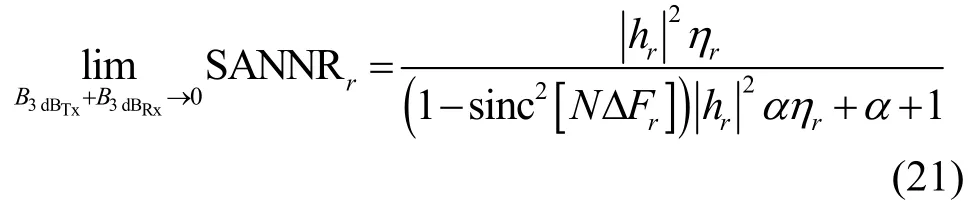
式(21)表征了合法接收機處不存在相位噪聲時的人工噪聲抑制性能,此時,SANNRr與主信道質量、功率分配因子、信道估計周期、頻率偏移有關。
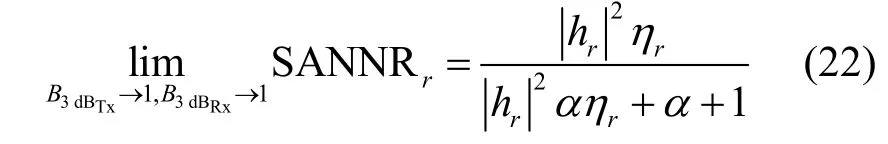
此時,SANNRr僅與主信道質量、功率分配因子有關,頻率偏移對人工噪聲抑制性能的影響可以被忽略。
3) 隨著信道估計周期N的增大,SANNRr整體呈下降趨勢。特別地,本文有如下結論。
①當N趨于1 時,SANNRr滿足
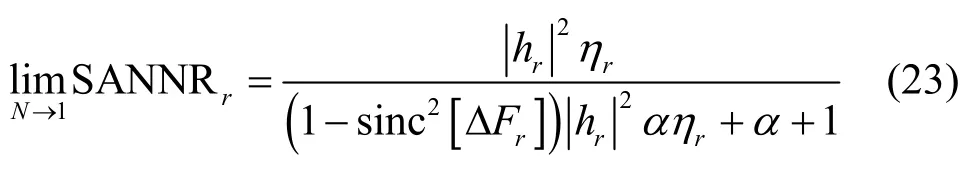
此時,SANNRr與主信道質量、功率分配因子、頻率偏移有關,與相位噪聲無關。
② 當N不斷增大且NΔFr? 1時,SANNRr滿足式(20)。此時,SANNRr僅與主信道質量、功率分配因子有關,頻率偏移與相位噪聲對抑制性能的影響可以被忽略。

此時,SANNRr與功率分配因子、頻率偏移、相位噪聲水平、信道估計周期有關。
2.2 保密容量性能
系統保密性能常用保密容量來評估[17]。記竊聽機處信噪比為SANNRe,表達式為
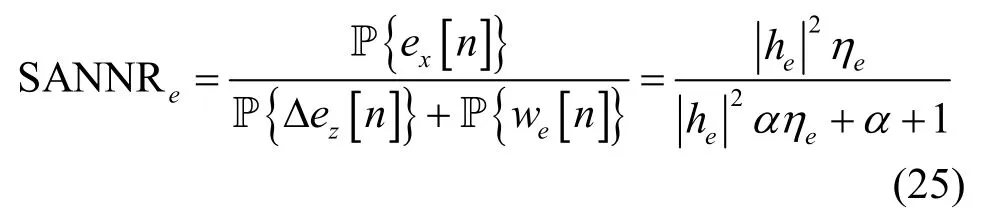
接著,由式(18)與式(25)可得命題3 中的結論。
命題3在圖1 所示的跳頻保密系統模型中,系統保密性能可以由保密容量指標來衡量。在頻相失配情形下,記跳頻系統的保密容量為Cs,表達式為
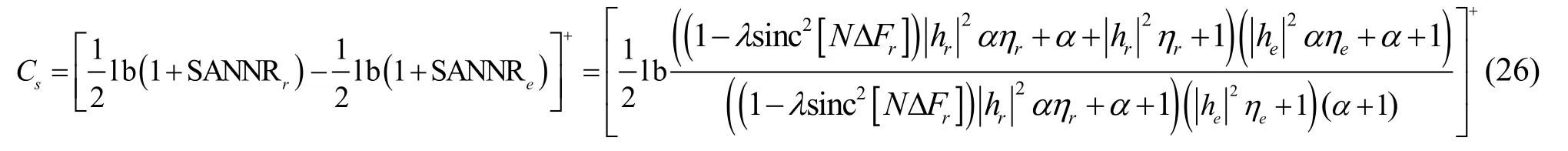
其中,[ ·]+=max { 0,·} 。由式(26)可得如下結論。
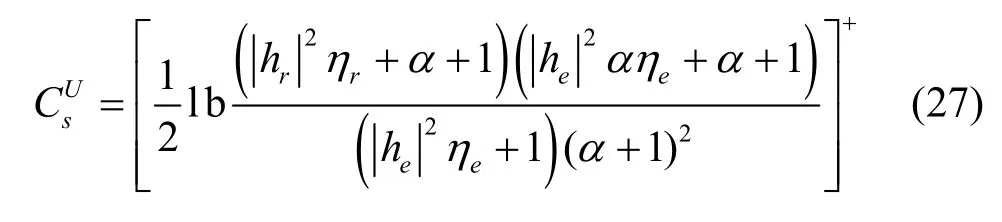
此時,系統保密容量僅與主信道與竊聽信道的質量、功率分配因子有關。
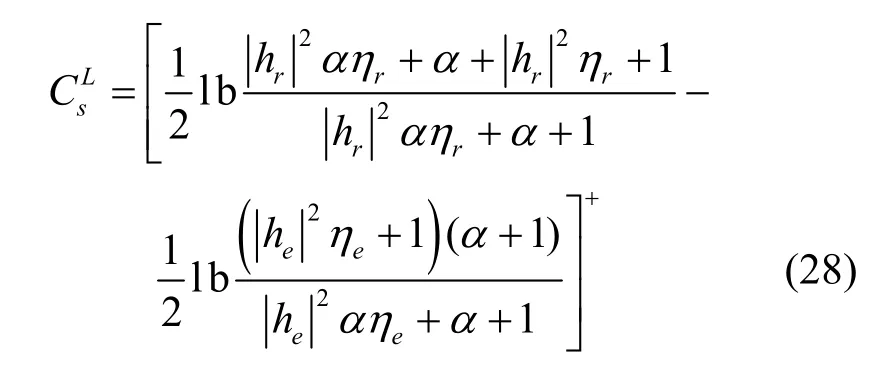
此時,系統保密容量僅與主信道與竊聽信道的質量、功率分配因子有關。
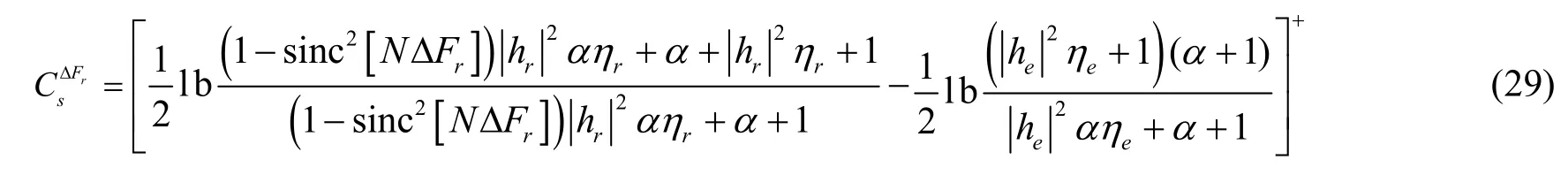
此時,系統保密容量與主信道與竊聽信道質量、功率分配因子、信道估計周期、頻率偏移有關。
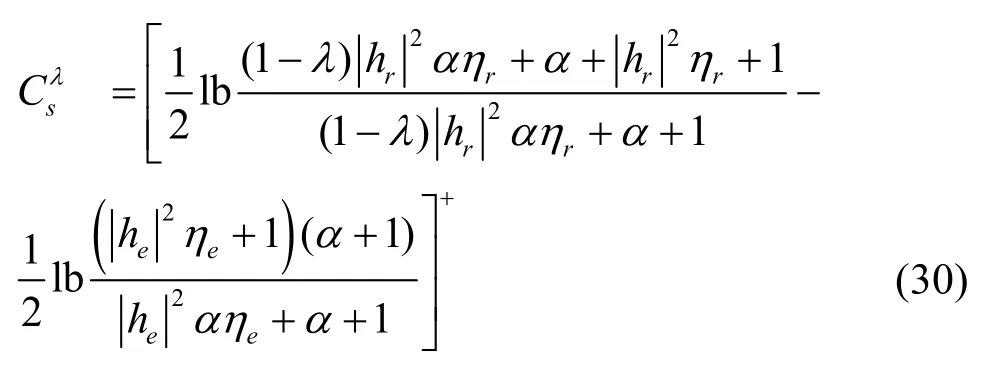
此時,系統保密容量與主信道與竊聽信道的質量、功率分配因子、信道估計周期、收發頻率振蕩器處3 dB 相干帶寬有關。
3 頻相失配穩健的功率分配及拓展
3.1 頻相失配穩健的功率分配方案
由上述分析可知,頻相失配會在合法接收機處引起人工噪聲抑制與保密性能損失,且損失程度與人工噪聲和保密信號的功率比有關。鑒于此,本節將研究具有頻相失配穩健的發射功率分配方案,在頻相失配情形下最大化系統保密容量。
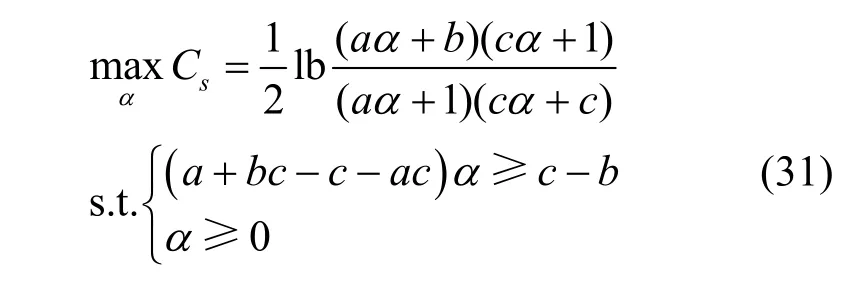
命題4在圖1 所示的跳頻保密系統模型中,具有頻相失配穩健性的發射功率分配方案為
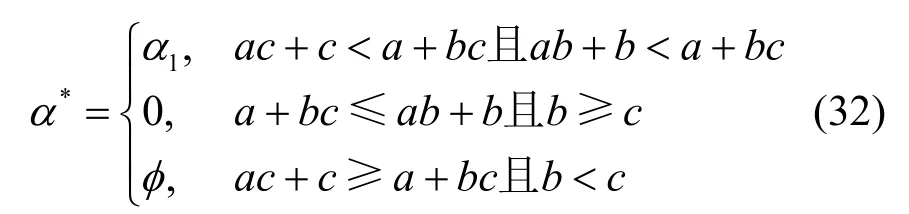
其中,α*=0 表示發射機只發送保密信號而不發送人工噪聲;*α=?表示發射機停止發送任何信號,因為此時系統的保密容量恒為零。α1的表達式為

④ 隨著信道估計周期N的增大,a呈增大趨勢。當N取值趨于 1 時,a趨于時,
⑤a與主信道質量呈正相關,隨著主信道質量的改善而不斷增大。
在實際應用中,不同的通信系統具有不同的頻相匹配度和傳播信道質量。鑒于此,接下來將針對不同場景對式(32)中的分配方案進行簡化與拓展。
3.2 不同頻相匹配度下的拓展方案
3.2.1 頻相完美匹配
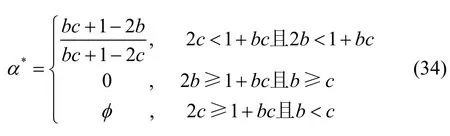
值得注意的是,當在功率優化過程中忽略頻相失配時,所得方案的表達式也為式(34)。但當存在頻相失配時,式(34)中的方案將不再適用,即該方案對頻相失配不具有穩健性。

3.2.2 頻相匹配度良好
在實際通信中,跳頻系統總存在頻率偏移與相位噪聲,很難實現頻相完美匹配。但是,部分接收機可以具有良好的頻率同步能力與較低的相位噪聲水平,使整體的頻相匹配度良好,即滿足此時頻率偏移與相位噪聲滿足,功率分配方案可以被簡化為
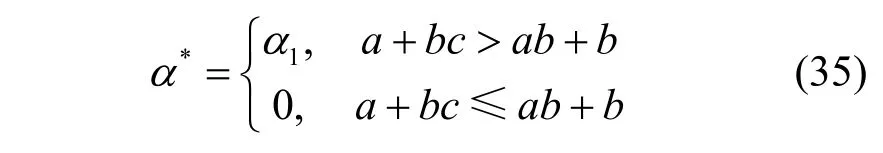
3.2.3 頻相匹配度較差
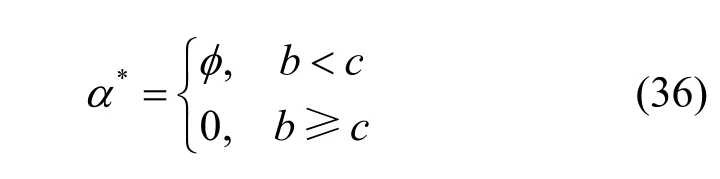
由式(36)可知,當系統的頻相匹配度和傳播信道質量均較差時,發射機最好同時停止發送任何信號,以防止保密信息被竊取。當系統頻相匹配度較差但傳播信道質量較好時,發射機應停止發送人工噪聲,只需發送保密信息,此時僅通過相對信道質量優勢就可以保證保密容量恒為正。
3.3 不同傳播信道質量下的拓展方案
3.3.1 主信道質量優于竊聽信道質量
當發射機與合法接收機間的主信道質量優于發射機與竊聽機間的竊聽信道質量,即時,可以得到b≥c,此時功率分配方案可以被簡化為
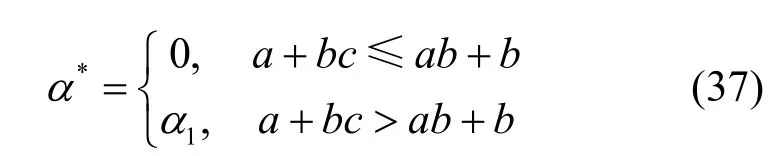
對于α*=0 情形,可以發現0,b>c。這表明當相對信道質量較好時,即使沒有傳輸人工噪聲,本文方案也可以保證系統保密容量恒為正。
3.3.2 主信道質量劣于竊聽信道質量
當發射機與合法接收機間的主信道質量優于發射機與竊聽機間的竊聽信道質量,即時,功率分配方案可以被簡化為
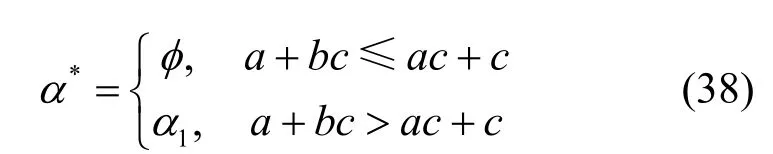
命題 5綜合考慮式(37)與式(38),當a+bc>ac+c且a+bc≈ac+c時,可以發現最優功率分配因子α*滿足

4 數值仿真
4.1 仿真條件
本節利用MATLAB 軟件進行仿真驗證,實驗參數設置如表1 所示。其中,主信道質量范圍大于常規跳頻通信系統,目的在于清晰展示傳統信道范圍內特性的同時,可以囊括全雙工系統自干擾信道[21]、協作通信系統協作干擾信道等[22],使所得結果具有更廣泛的參考價值。此外,每跳符號數在保證清晰展示跳頻系統常用范圍的同時,通過設置每跳最大符號數遠大于1,使仿真分析結論廣泛適用于定頻、跳頻系統。為了更清晰地呈現仿真結果而不失一般性,下述仿真中假設合法接收機和竊聽機處的頻率偏移與相位噪聲水平相同,即

表1 實驗參數設置
4.2 人工噪聲抑制性能仿真
圖2通過對頻相失配下接收信號的信噪比特性進行仿真,衡量了合法接收機處人工噪聲抑制性能。4個子圖中,發射功率分配因子均為1,即人工噪聲與保密信號等功率發射。首先,圖2(a)針對接收信噪比SANNRr與頻率偏移 ΔF的關系進行了仿真。隨著頻率偏移的增大,SANNRr呈下降趨勢,表明頻率偏移會降低合法接收機處人工噪聲抑制性能。當頻率偏移取值趨于零時,SANNRr逐漸收斂至式(19)中的理論值;隨著頻率偏移的增大,當NΔF? 1時,SANNRr逐漸收斂至式(20)中的理論值,驗證了理論分析的正確性。接著,通過對比曲線①②③可以發現,改善主信道質量有助于弱化頻率偏移對人工噪聲抑制性能的負面影響;通過對比曲線④⑤⑥可以發現,相位噪聲水平的抬升會加劇頻率偏移的負面影響;通過對比曲線③④可以發現,縮短信道估計周期可以顯著減弱由頻率偏移引起的SANNRr損失。
圖2(b)展示了SANNRr隨收發頻率振蕩器處3 dB相干帶寬B3dB的變化趨勢,進而衡量相位噪聲水平對人工噪聲抑制性能的影響程度。從圖2(b)中可以發現,SANNRr隨著B3dB的增大而不斷減小,表明收發頻率振蕩器處的相位噪聲會降低合法接收機處人工噪聲抑制性能。當B3dB趨于零時,SANNRr逐漸收斂至式(21)中的理論值;隨著相位噪聲水平的不斷抬升,當B3dB取值趨于1 時,SANNRr逐漸收斂至式(22)中的理論值,驗證了理論分析的正確性。接著,通過對比曲線④⑤⑥可以發現,頻率偏移的增大會加劇相位噪聲的負面影響,驗證了圖2(a)中的結論;通過對比曲線①②③可以發現,改善主信道質量可以有效緩解相位噪聲對SANNRr性能的負面影響;通過對比曲線③④可以發現,縮短信道估計周期可以顯著減弱由相位噪聲引起的SANNRr損失。
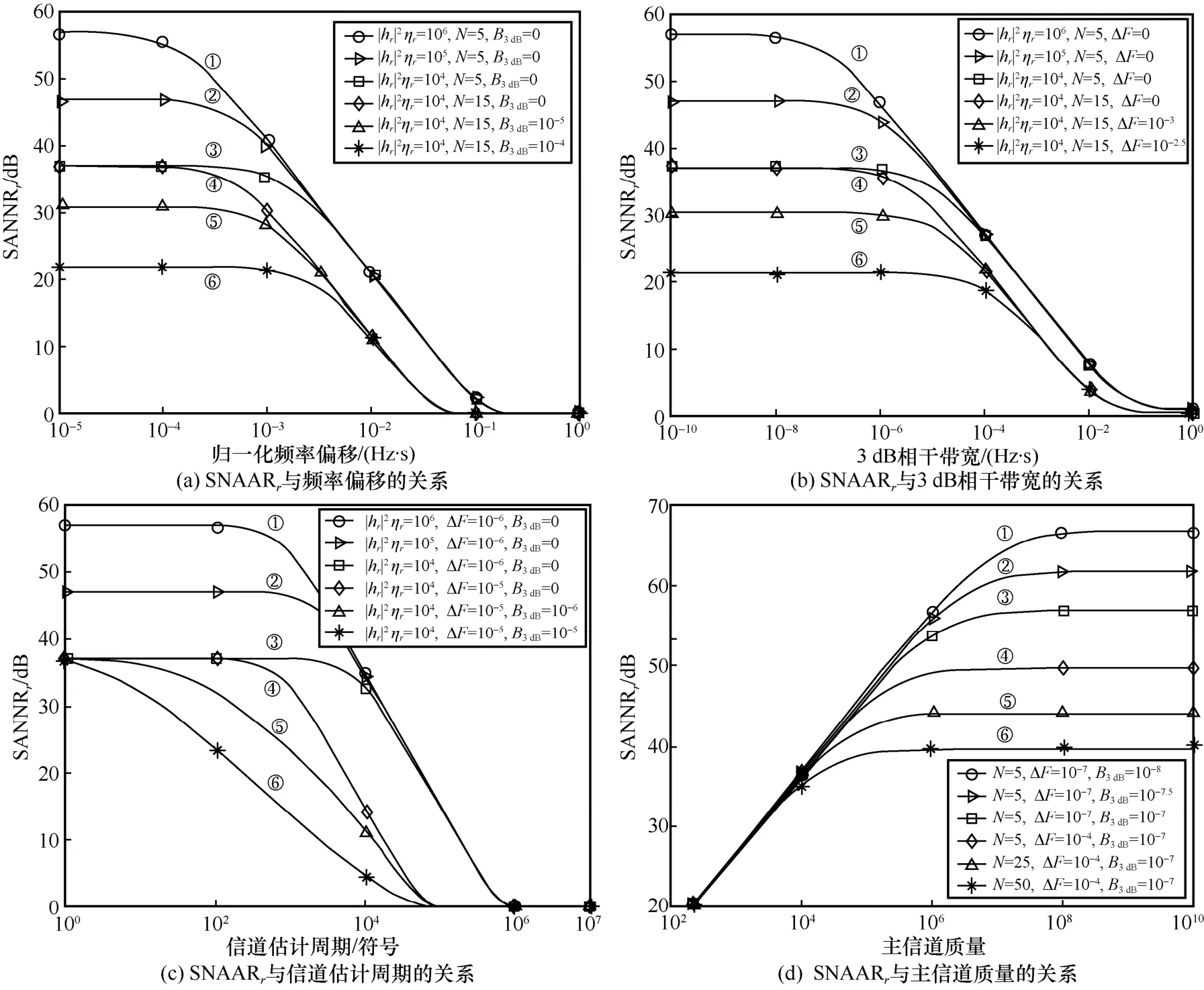
圖2 合法接收機人工噪聲抑制性能分析
圖2(c)展示了SANNRr與信道估計周期N的關系。從圖2(c)中可以發現,SANNRr隨著N的減小而不斷增大,表明縮短信道估計周期可以有效地提升合法接收機處的人工噪聲抑制性能。當N取值趨于1 時,SANNRr逐漸收斂至式(23)中的理論值。隨著信道估計周期的不斷增大,當NΔF? 1時,SANNRr逐漸收斂至式(20)中的理論值。接著,通過對比曲線①②③可以發現,改善主信道質量可以提升由縮短N獲得的SANNRr性能增益;通過對比曲線④⑤⑥可以發現,相位噪聲水平的抬升會降低由縮短N獲得的SANNRr性能增益,驗證了圖2(b)中的結論;通過對比曲線③④可以發現,提升合法接收機處頻率同步性能可以顯著減弱相位噪聲的負面影響,驗證了圖2(a)與圖2(b)的結論。
圖2(d)展示了SANNRr與主信道質量的關系。從圖2(d)中可以發現,SANNRr隨著主信道質量的改善而不斷增大,表明提升主信道質量有利于增強合法接收機處的人工噪聲抑制性能。隨著主信道質量的不斷增大,當α+1時,SANNRr趨于式(24)中的理論值。通過對比曲線①②③可以發現,相位噪聲水平的抬升會顯著降低通過提升獲得的SANNRr增益;類似地,通過對比曲線④⑤⑥可以發現,縮短信道估計周期可以有效地提升通過改善主信道質量獲得的SANNRr增益;通過對比曲線③④可以發現,提升合法接收機處的頻率同步能力可以顯著減弱相位噪聲的負面影響,驗證了圖2(a)~圖2(c)中的結論。
4.3 最優功率分配因子特性仿真
圖3 對最優功率分配因子α*的特性進行了仿真,進而分析頻相失配下人工噪聲與保密信號的發射功率分配方案。首先,圖3(a)針對α*與頻率偏移的關系進行了仿真。從圖3(a)中可以發現,隨著 ΔF的增加α*整體呈下降趨勢,表明隨著頻率偏移的增大,應逐步降低人工噪聲與保密信號的發射功率比,以緩解因頻率偏移引起的保密性能損失。當頻率偏移取值趨于零時,α*逐漸收斂至常數。隨著頻率偏移的增大,當且趨于0+時,α*收斂至+∞;在其他仿真條件下,α*逐漸收斂至0,驗證了式(39)的結論。通過對比曲線①②③可以發現,α*應隨著主信道與竊聽信道間的相對信道質量的改善而不斷減小,以弱化頻率偏移對人工噪聲抑制性能的負面影響;通過對比曲線④⑤⑥可以發現,α*應隨著相位噪聲的惡化而不斷減小;通過對比曲線③④可以發現,α*隨著信道估計周期的增大而減小,以提升系統對頻率偏移的穩健性。
圖3(b)展示了α*隨收發頻率振蕩器的3 dB 相干帶寬B3dB的變化趨勢,進而衡量相位噪聲水平對α*的影響程度。從圖3(b)中可以發現,隨著B3dB的增大,α*整體呈下降趨勢,表明α*隨著相位噪聲水平的抬升而不斷減小;當B3dB趨于零時,α*逐漸收斂至常數值。通過對比曲線①②③可以發現,人工噪聲與保密信號的發射功率比應隨著主信道質量的改善而不斷降低;通過對比曲線③④可以發現,縮短信道估計周期會增大最優功率分配因子的取值;通過對比曲線④⑤⑥可以發現,α*隨著頻率同步性能的惡化而不斷減小,驗證了圖3(a)中的結論。
圖3(c)展示了α*與信道估計周期N的關系。從圖3(c)中可以發現,隨著N的增加,α*整體呈下降趨勢,表明隨著信道估計周期的增大,應逐步降低人工噪聲與保密信號的發射功率比,以減弱由頻相失配引起的系統性能下降。隨著信道估計周期的增大,當且趨于0+時,曲線①中α*收斂至+∞,驗證了式(39)的結論;在其他仿真條件下,α*逐漸收斂至0。接著,從曲線①②③可以發現,α*隨著相對信道質量的改善而不斷減小;從曲線④⑤⑥可以發現,相位噪聲水平的抬升會減小α*的取值,驗證了圖3(a)與圖3(b)中的結論;從曲線③④可以發現,對于特定的信道估計周期,α*隨著頻率同步性能的惡化而不斷減小。
圖3(d)展示了α*與主信道質量的關系。從圖3(d)中可以發現,α*隨著的改善而不斷減小。通過對比曲線①②③可以發現,α*的取值隨著竊聽信道質量的提升而增大,表明強竊聽場景中應增大人工噪聲功率以阻塞非法竊聽;通過對比曲線④⑤可以發現,縮短信道估計周期會增大α*的取值,進而增加人工噪聲的發射功率消耗;通過對比曲線⑤⑥可以發現,α*隨著頻率偏移的增大而減小;通過對比曲線⑥⑦⑧可以發現,α*隨著相噪水平的抬升而不斷減小,驗證了圖3(a)~圖3(c)中的結論。
4.4 所提方案保密性能仿真
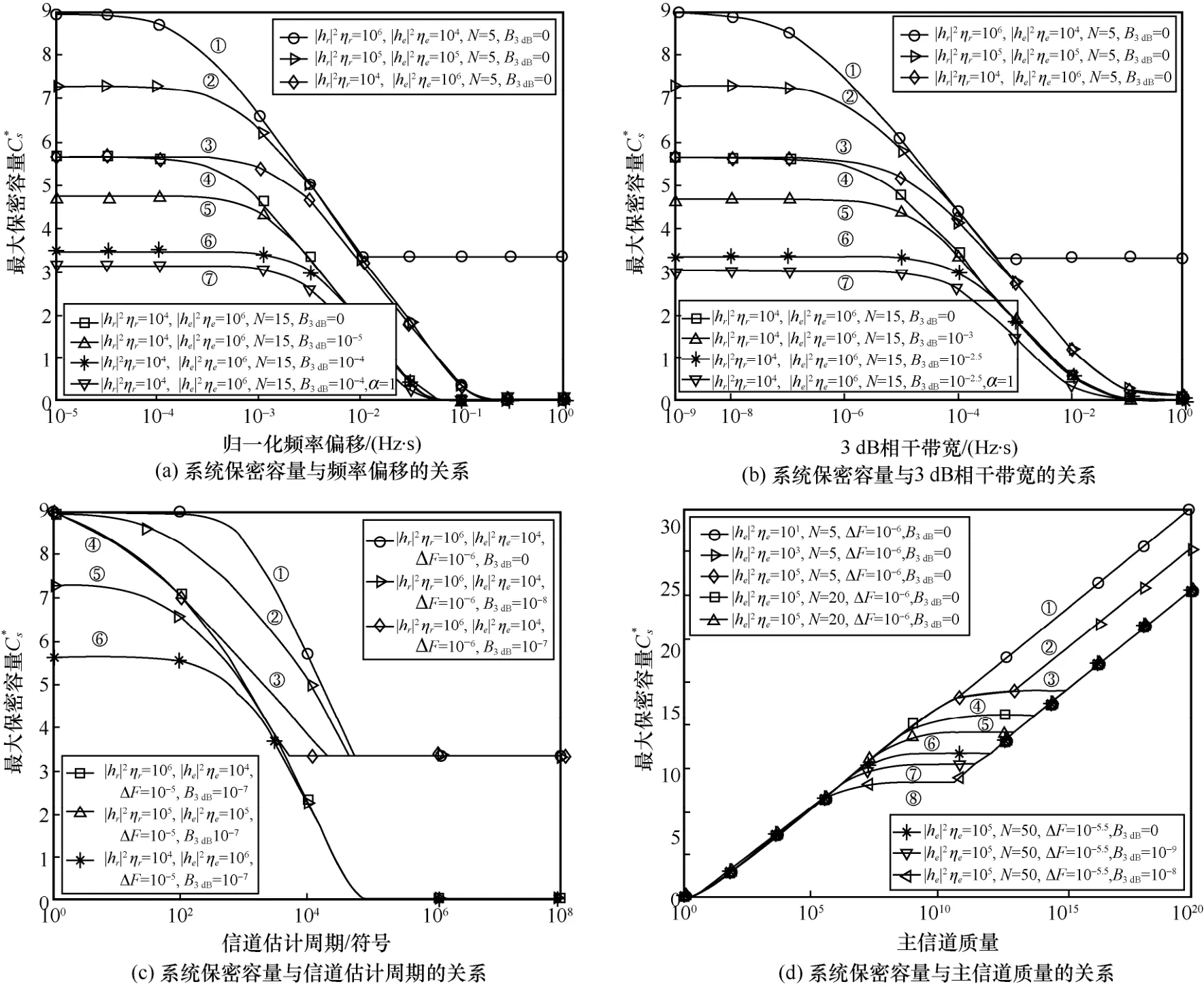
圖4 頻相失配下系統保密容量性能
5 結束語
本文對人工噪聲掩護的跳頻保密系統中頻相失配問題進行了數學建模,采用信噪比指標衡量了頻相失配下系統的人工噪聲抑制性能,并采用保密容量指標衡量了系統的保密性能。在此基礎上,提出了具有頻相失配穩健性的發射功率分配方案,并根據不同的頻相匹配度與傳播信道質量對其進行了簡化與拓展。研究發現,頻相失配問題會顯著降低接收機處人工噪聲抑制能力與系統保密性能。隨著頻相失配問題的惡化,應逐步降低人工噪聲與保密信號的發射功率比例以緩解由頻相失配引入的系統性能損失。此外,通過縮短信道估計周期或者抬升合法收發信機間的主信道質量,可以有效擴大通過功率優化帶來的保密容量增益。本文研究可以為復雜電磁環境下的保密通信、跳頻系統設計與部署提供理論支撐。后續研究中,一方面可以綜合考慮其他非理想因素的影響,另一方面可以通過優化人工噪聲抑制流程進一步提升系統性能。
附錄1 命題4 中功率分配方案證明
本節將給出式(32)中的最優功率分配方案的證明。式(26)中Cs關于α的一階導數為


情形3 最后考慮A< 0情形,此時a+bc>ac+c。當b<c時,式(31)的可行域為α∈[α0,+∞);當b≥c時,可行域為α∈ [0,+∞)。
當Aα2+Bα+C=0關于變量α有解時,將解記為α1和α2,且α1與α2可以分別表示為式(33)和式(43)。

整合上述 3 種情形,可得α*=?的條件為a+bc≤ac+c且b<c;并且,α*在2 種情形下取值為零,第一種是a+bc≤ac+c且b≥c,第二種 是a+bc>ac+c,b≥c且c(a+bc)≤b(ac+c),這2 種情形可以整合為a+bc≤ab+b且b≥c;此外,α*在2 種情形下取值為α1,第一種是a+bc>ac+c且b<c,第二種是a+bc>ac+c,b≥c且c(a+bc) >b(ac+c),這2 種情形可以整合為ac+c<a+bc且ab+b<a+bc。經過上述整合,即可得到式(32)中的結論。
證畢。
附錄2 命題5 推導證明
式 (39) 的成立 條件為a+bc>ac+c,且a+bc≈ac+c。首先分析α*的取值特征如下。
①若b>c,此時主信道質量優于竊聽信道質量,且a+bc≈ac+c<ab+b。由式(37)可知,此時α*=0。
②若b=c,此時主信道質量與竊聽信道質量相當,且a+bc>ac+c=ab+b。由式(37)可知,此時α*=α1。
③若b<c,此時主信道質量劣于竊聽信道質量。由式(38)可知,a+bc>ac+c時α*=α1。至此,可得
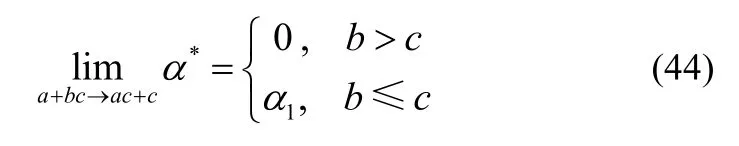
接著,對α1的特征展開分析。令a+bc=ac+c+Δ,其中Δ> 0且Δ≈ 0,可以得到

綜合式(44)與式(48),可得式(39)中的結論。
證畢。

