內(nèi)河航道寬度確定若干方法探索

王家宏，王偉軍，艾萬政

（浙江海洋大學(xué)，浙江 舟山 316022）

航道是船舶通航的載體，其主要功能就是為船舶通航服務(wù)。相關(guān)統(tǒng)計(jì)資料表明，大約15%的交通事故是由于航道缺陷造成的。因此合理改造航道，科學(xué)布置航道浮標(biāo)，是確保船舶通航安全的重要前提之一。對于內(nèi)河航道浮標(biāo)設(shè)置而言，最重要的是航道兩邊的邊界浮標(biāo)設(shè)置問題。航道兩邊界浮標(biāo)之間的間距安排，與航道寬度密切相關(guān)。如果航道兩邊界浮標(biāo)之間的距離設(shè)置較大，就會(huì)浪費(fèi)航道資源；如果航道兩邊界浮標(biāo)間距過小，就會(huì)影響到船舶的通航安全。因而航道邊界浮標(biāo)設(shè)置力求合理科學(xué)。眾所周知，影響內(nèi)河航道寬度的主要因素包括代表船型船舶的航跡帶寬度、船間間距、船岸間距和附加寬度等。目前我國內(nèi)河通航標(biāo)準(zhǔn)對我國內(nèi)河航道寬度都有明確的界定[1-3]。在該標(biāo)準(zhǔn)中，船舶的航跡帶寬度、船間間距和船岸間距等參數(shù)都是以代表船型尺度（船長、船寬）來確定的。毋庸置疑，船舶的航跡帶寬度與船舶的長度、寬度和偏航角相關(guān)，航跡帶寬度完全可用通航船舶的長度和寬度來確定。而關(guān)于航道的附加寬度，內(nèi)河通航標(biāo)準(zhǔn)中并沒有明確界定，尤其是天然彎曲航道的附加寬度，標(biāo)準(zhǔn)中只是提到，可考慮以順直航道寬度為基礎(chǔ)且適當(dāng)加寬，但究竟以加寬多少為標(biāo)準(zhǔn)，內(nèi)河通航標(biāo)準(zhǔn)中并沒有直接界定。不少學(xué)者認(rèn)為，航道的附加寬度主要是風(fēng)、流等因素對船舶造成的漂移量。有關(guān)順直航道的風(fēng)致漂移量和流致漂移量，目前研究成果較多，在順直航道浮標(biāo)設(shè)置中可直接借鑒運(yùn)用[4-7]。但是對于彎曲航道而言，由于彎道環(huán)流的流向、流速均隨水深的變化而變化，因此彎道船舶的流致漂移量如何確定，則有待于進(jìn)一步研究[5]。關(guān)于船間間距、船岸間距，其大小與船間效應(yīng)、岸壁效應(yīng)密切相關(guān)，而船間效應(yīng)、岸壁效應(yīng)是2個(gè)非常復(fù)雜的問題，其不但與通航船舶的尺度相關(guān)，而且還與水流條件密切相關(guān)。因此單純以船舶尺度去確定船間間距和船岸間距，明顯顯得不夠合理。為此，關(guān)于內(nèi)河航道寬度的確定，重點(diǎn)是要解決船間間距、船岸間距及彎道流致漂移量等問題。由此看來，有必要緊緊圍繞船舶通航安全去討論船間間距、船岸間距及彎道流致漂移量等問題，以便為內(nèi)河航道寬度的確定奠定基礎(chǔ)，以減少交通事故發(fā)生的概率。

1 船間間距和船岸間距的確定方法

1.1 概率論確定方法

船間效應(yīng)和岸壁效應(yīng)非常復(fù)雜，二者分別與船間間距和船岸間距密切相關(guān)。目前關(guān)于船間效應(yīng)和岸壁效應(yīng)，雖然研究成果較多，但這些成果多數(shù)只限于定性分析層面，關(guān)于船間效應(yīng)和岸壁效應(yīng)的數(shù)學(xué)模型或經(jīng)驗(yàn)公式，目前幾乎還沒見到。由于船間效應(yīng)和岸壁效應(yīng)的復(fù)雜性，所以也很難從定量層面去確定船間間距和船岸間距的大小。如果換位思考，概率論的相關(guān)知識為此提供了較好的解決辦法。

圖1表明了相遇船舶的狀況。x1表示；若下水船舶偏離航道軸線，其概率值可用x2表示。x1和x2無關(guān)，且都服從正態(tài)分布，且x1和x2是隨機(jī)變量，也就是說某船偏離航道軸線是隨機(jī)的，與另一條不相關(guān)。圖1表明

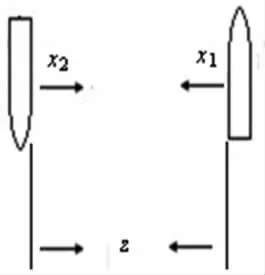
圖1 相遇船舶

式中：z0為相會(huì)船舶應(yīng)保持的合理間距。式（1）說明，如果z>0，即x1+x2z0，相遇的2條船舶不可避免存在碰撞危險(xiǎn)。如果設(shè)置

則綜合x1的正態(tài)分布函數(shù)f（x1）及x2的正態(tài)分布函數(shù)f（x2），可以得到

式（3）可改寫為

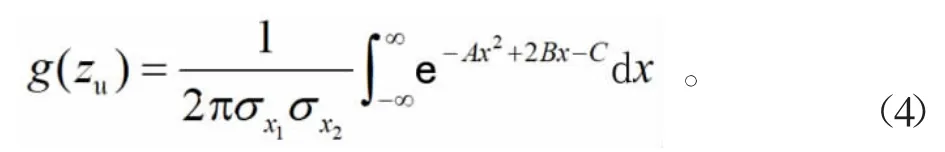
式（4）中

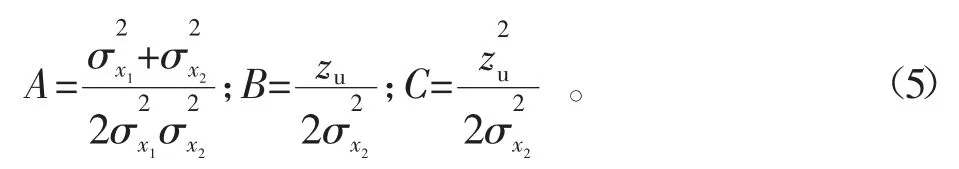
應(yīng)用伯努利-泊松間距公式，可得到

從式（8）可以看出，正態(tài)分布規(guī)律適用于2條相遇船舶的橫間距分布。因此相遇船舶發(fā)生碰撞概率可以表達(dá)為

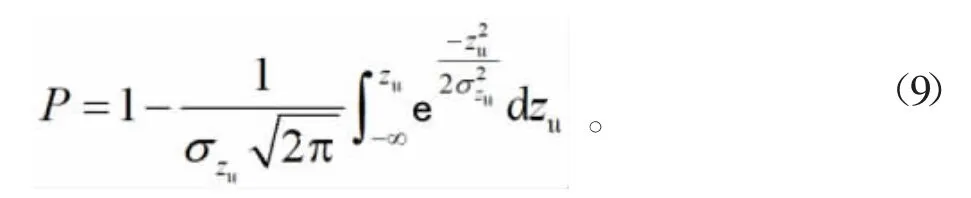
如果設(shè)定：dzu=σzu v，則式（9）可以變形為

引入拉普拉斯參數(shù)

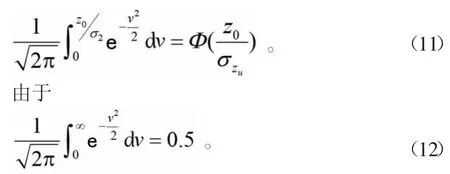
結(jié)合式（10）、式（11）和式（12）可得

式（13）明確表明，在已經(jīng)知道航道事故概率P的情況下（此值可根據(jù)航道設(shè)計(jì)要求預(yù)先設(shè)定），則可得到相應(yīng)的z0，此時(shí)船間間距也就完全確定。例如，如果在航道規(guī)劃時(shí)，預(yù)計(jì)船舶碰撞概率預(yù)定為0.005，即P=0.005。則按照式（13），可以認(rèn)為

根據(jù)式（13）可求解得到

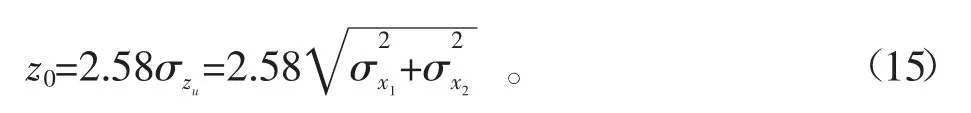
如果認(rèn)為船舶上、下水航行準(zhǔn)確性一致，在這種預(yù)定情況下，可設(shè)置σx1=σx2，因此式（15）經(jīng)過推導(dǎo)可得到

相關(guān)研究表明，均方差σx與船舶的尺度有關(guān)，其大小可以根據(jù)航道內(nèi)多年船舶通航觀測數(shù)據(jù)確定。按照上述同樣的方法，船岸間距也完全可用類似的方法確定。但此方法要基于大量統(tǒng)計(jì)數(shù)據(jù)，對于新開辟的航道不一定完全適用。對于老航道的改進(jìn)，則還有一定的指導(dǎo)意義。

1.2 船舶領(lǐng)域理論確定方法

日本籍學(xué)者藤井彌平在詳細(xì)調(diào)查日本近海船舶的相對位置時(shí)，在經(jīng)過認(rèn)真分析的基礎(chǔ)上，得出了一種模型，即船舶領(lǐng)域模型。船舶領(lǐng)域模型理論認(rèn)為，船舶領(lǐng)域是以船舶為中心的橢圓形區(qū)域，該區(qū)域的長軸是船舶中心縱軸線，而短軸是與長軸相垂直的船舶中心的橫軸線。船舶領(lǐng)域的尺度如下：長軸大約為7倍船長，短軸為3倍船長，而船舶位于該領(lǐng)域的中心。在一般的船舶追越局面中，相對水域足夠，被追越船的船舶領(lǐng)域尺度可適當(dāng)認(rèn)為較寬，船舶領(lǐng)域長軸取8倍船長，短軸取3.2倍正橫距，這有利于船舶防撞。如果船舶航行到速度受限的水域，如港區(qū)、狹水道和狹窄海峽，此時(shí)船舶領(lǐng)域尺度可能大大減小，此時(shí)船舶領(lǐng)域的長軸一般取6倍船長，短軸一般取1.6倍正橫距。

Goodwin在認(rèn)真研究藤井彌平船舶領(lǐng)域模型的基礎(chǔ)上，最終創(chuàng)立了一套改進(jìn)的船舶領(lǐng)域模型，該模型較好地適用于寬闊水域（該模型如圖2所示）。其運(yùn)用船員培訓(xùn)機(jī)器及倫敦帝國理工學(xué)院雷達(dá)模擬器，進(jìn)行了大量的船舶碰撞方面的試驗(yàn)，并對北海南部區(qū)域的船舶交通進(jìn)行調(diào)查，其調(diào)查方法與日本學(xué)者藤井彌平類似，并最終認(rèn)為，《1972國際海上避碰規(guī)則》對船舶的行動(dòng)有著較大的影響。從避碰規(guī)則來看，規(guī)則按照來船方位區(qū)別，對不同的避讓行動(dòng)進(jìn)行了規(guī)定。因而可見，藤井彌平的船舶橢圓形領(lǐng)域模型有著不完善的地方，船舶領(lǐng)域的幾何圖形不應(yīng)該是對稱的。Goodwin在總結(jié)船舶號燈顯示范圍的基礎(chǔ)上，重新劃分了船舶領(lǐng)域，其領(lǐng)域范圍如圖2所示。其船舶領(lǐng)域模型充分考慮了《1972年國際海上避碰規(guī)則》對船舶行動(dòng)行為的要求。無論是藤井彌平船舶領(lǐng)域模型還是Goodwin的船舶領(lǐng)域模型，都是通過分析大量數(shù)據(jù)得出的，對船舶安全航行具有指導(dǎo)意義。在確定內(nèi)河船間間距及船岸間距時(shí)，也可以參考船舶領(lǐng)域理論，將船舶橫向領(lǐng)域的最大范圍作為船間間距及船岸間距的參考量。船舶領(lǐng)域可以用來設(shè)計(jì)航道的寬度，但該理論是日本學(xué)者統(tǒng)計(jì)日本航道情況而得出的，對于其他航道是否適用，還有待于進(jìn)一步探索。因?yàn)楹降缹挾鹊拇_定與航道特定水流條件密切相關(guān)，船舶領(lǐng)域理論雖然有一定的指導(dǎo)意義，但其普遍適用性還需要進(jìn)一步驗(yàn)證。

圖2 Goodwin模型

2 彎道流致漂移量確定方法

在天然彎曲航道存在彎道環(huán)流，這種環(huán)流正是引起船舶橫向漂移的重要因素。在確定航道寬度時(shí)，應(yīng)該將彎道環(huán)流引起的船舶橫向漂移量考慮進(jìn)去，這樣有利于保證船舶運(yùn)行安全。彎道環(huán)流與普通的橫流不同之處在于：彎道環(huán)流的面流流向凹岸，隨著水深的增加，環(huán)流逐步減小，當(dāng)水深到達(dá)某一深度時(shí)，環(huán)流開始反向（從凹岸流向凸岸）并逐漸加大。彎道環(huán)流的這一特性，決定了其對吃水不同船舶產(chǎn)生的橫向漂移量不一樣。彎道環(huán)流可用公式表示為

式中：U為彎道縱向流速；H為彎道水深；y=z/H為相對水深用（水深起算點(diǎn)被認(rèn)為從河底開始）；r為彎道曲率。在彎道存在彎道橫流，其底流流向凸岸，面流流向凹岸，面流和底流流向相反，因而，船舶吃水為d時(shí)，通過數(shù)學(xué)推導(dǎo)可知，作用于船體上的平均彎道環(huán)流流速可表達(dá)為

式中：ud為船體上的平均彎道環(huán)流流速。綜合式（17）及式（18），可以導(dǎo)出

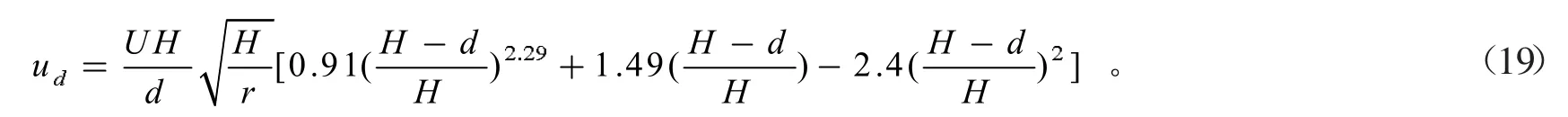
式（19）表明，作用在船體上的平均彎道環(huán)流流速由彎道曲率、平均縱向流速、彎道水深和船舶吃水共同確定。將式（19）應(yīng)用到順直航道船舶流致漂移量公式中，即可計(jì)算出彎道船舶流致漂移量。該方法本文相關(guān)作者曾在別的文獻(xiàn)中提及過，但計(jì)算程序較為繁瑣，適用性還不夠理想。

3 船橋間距確定方法

內(nèi)河橋區(qū)航道往往也是事故多發(fā)地段。對于橋區(qū)航道而言，橋墩與航道邊界浮標(biāo)之間的間距也是航道寬度設(shè)計(jì)時(shí)的重要考慮因素。內(nèi)河航道建橋以后，由于橋墩的存在，水流結(jié)構(gòu)變得復(fù)雜，航行安全隱患也增加。橋墩附近的水流結(jié)構(gòu)如圖3所示。一般認(rèn)為，橋墩紊流漩渦區(qū)是船舶通航應(yīng)回避的區(qū)域[7-8]。因此也有人認(rèn)為橋區(qū)航道應(yīng)布置在橋墩紊流漩渦區(qū)之外，也可以說，橋墩紊流漩渦區(qū)的橫向最大范圍應(yīng)是船橋之間應(yīng)保持的最小距離。關(guān)于橋墩紊流漩渦區(qū)范圍，相關(guān)研究較多，可選用適當(dāng)?shù)慕?jīng)驗(yàn)計(jì)算模型確定，計(jì)算確定的橋墩紊流漩渦區(qū)范圍，完全可應(yīng)用到橋區(qū)航道寬度設(shè)計(jì)之中。但橋墩紊流是非常復(fù)雜的問題，從通航的角度如何確定其范圍，相關(guān)專家說法不一。因此關(guān)于橋墩紊流對通航的影響，有待于科學(xué)試驗(yàn)的驗(yàn)證。

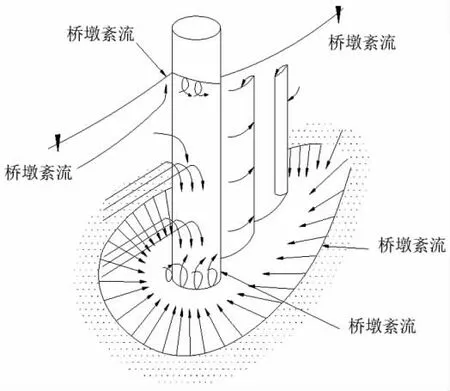
圖3 橋墩水流結(jié)構(gòu)

4 結(jié)論

內(nèi)河航道寬度布置涉及到船舶的通航安全。對于內(nèi)河航道寬度而言，最關(guān)鍵的是如何確定船間間距、船岸間距、彎道流致漂移量及船橋間距。而船間間距、船岸間距、彎道流致漂移量及船橋間距與多種影響因素相關(guān)，難以單純從定量角度去確定。本文結(jié)合船舶操縱特性，從概率論角度和船舶領(lǐng)域理論角度提出了確定船間間距和船岸間距的方法；從水動(dòng)力學(xué)角度提出了彎道流致漂移量確定方法和船橋間距確定方法。本文的以上研究方法和手段，為研究其他航道問題提供了一種全新的視野，但相關(guān)方法也有其局限性，需要進(jìn)一步研究。