彈膛偏移對小口徑埋頭槍彈擠進動態響應的影響

許輝， 張瑞潔， 蔣明飛， 劉坤， 吳志林

(南京理工大學 機械工程學院， 江蘇 南京 210094)

0 引言

埋頭彈- 槍系統是單兵武器輕量化的關鍵技術之一，使用聚合物藥筒和埋頭彈技術，可有效降低彈- 槍系統的外形尺寸及質量，對減輕單兵負載、提高作戰效能具有重大的軍事意義。

為適應埋頭彈圓柱狀外形，埋頭彈- 槍系統多采用擺動彈膛或升降彈膛的結構設計，以實現順利供彈和退殼動作。彈/線膛分離的結構致使彈膛軸線與線膛(槍管)軸線之間存在偏差，這種彈膛偏移現象(彈/線膛不同軸)會改變彈頭的入膛姿態，在彈頭擠進入膛過程中產生質心偏量和姿態偏角，導致彈頭在出膛口時產生橫向擺動和氣動跳躍，甚至導致膛壓異常現象，對武器射擊精度、壽命及安全性產生極大影響。隨著槍械系統的迅速發展，亟待開展埋頭彈- 槍系統動態擠進過程研究。

近年來，埋頭彈- 槍系統受到廣泛關注，國內外學者相繼開展了埋頭彈內彈道特性及膛內運動規律研究。Lu等建立了埋頭彈兩相流內彈道模型，研究了埋頭彈起始彈道階段發射藥燃燒及彈頭運動，并通過試驗驗證了數值計算模型的正確性。Nusca等采用數值模擬的方法，考慮燃氣在彈體四周的分布及流動情況，分析了埋頭彈膛內壓力波的形成和瞬態彈丸載荷。Wang等將遺傳算法引入到埋頭彈內彈道的優化設計中，以最大膛壓及膛口初速作為優化目標，對埋頭彈藥室容積和裝填密度進行了優化設計。Cao等基于高速攝像技術設計了埋頭彈起始彈道測試系統，定量研究了彈頭的位移、速度、加速度及運動姿態等。Corriveau等為研究彈/線膛不同軸對埋頭彈槍精度的影響，設計了可調整彈膛偏移量的彈道槍，并進行了埋頭彈準確度和密集度測試，認為彈膛偏移量導致了彈頭膛內偏角的產生，進而影響了埋頭彈槍系統的精度。王惠源等通過有限元方法分析了不同入膛姿態下的彈頭膛內運動及槍口擾動規律，認為彈頭膛內姿態角對射擊精度有重要影響。上述成果為埋頭彈- 槍系統擠進過程的研究奠定了基礎。但現有工作主要集中于埋頭彈內彈道特性及裝藥技術，對于埋頭槍彈擠進過程的動態響應有待開展更深層次的研究。

本文通過數值模擬和試驗驗證相結合的方法，開展埋頭彈- 槍系統動態擠進過程研究。采用耦合內彈道的顯式動力學有限元方法，建立埋頭彈擠進過程彈- 槍相互作用有限元模型，分析彈膛偏移量對彈頭膛內運動姿態及內彈道特性的影響規律，對彈帽結構參數開展優化設計，并采用姿態測量試驗及精度試驗驗證優化方案的有效性。研究成果為埋頭彈- 槍系統設計及優化提供技術支撐。

1 埋頭彈擠進過程有限元模型

1.1 物理模型與基本假設

參照文獻[12]中5.56 mm埋頭彈的主體結構，設計了本文所研究的5.8 mm埋頭彈結構，如圖1所示。主要部件包括彈帽、彈頭、彈殼、發射藥、底火座、底火等。其中，彈帽在發射時給彈頭提供定位、導向及閉氣作用。彈帽中心為光滑圓孔，其口部設有倒角，以保證彈丸順利通過，防止射擊過程中產生卷邊現象。彈帽抱彈部設有環狀收口，在組裝成彈時起到定位作用，同時提供一定的拔彈力。

圖1 埋頭彈結構Fig.1 Structure of cased telescoped ammunition

埋頭彈擠進過程三維實體模型如圖2所示。由圖2可知，采用擺膛結構的埋頭彈槍，其彈膛與槍管分離，埋頭彈安置在彈膛內，彈帽緊貼槍管尾端面，彈頭由抱彈部在彈帽中定位。埋頭彈發射時，發射藥燃燒產生的高溫高壓燃氣作用于彈頭底部，彈頭在彈帽的導向作用下向前運動。經過一段自由行程，彈頭圓柱部逐漸擠進膛線并形成刻痕，隨后在槍管的歸正與導轉作用下飛離膛口。

圖2 埋頭彈擠進過程三維實體模型Fig.2 3D model of the engraving process of a cased telescoped ammunition bullet

根據埋頭彈擠進過程的特點，有限元建模時引入如下假設：

1)忽略彈膛與彈帽之間的間隙，忽略槍管后坐，不考慮溫度應力場；

2)槍管、彈帽及彈頭各部件材料各向同性；

3)考慮彈帽及彈頭彈塑性變形，其屈服強度服從Mises屈服準則；

4)忽略火藥燃氣對彈- 槍系統的熱力場影響。

1.2 網格劃分

依據埋頭彈- 槍系統的槍管、彈膛、彈帽與彈頭結構尺寸參數建立三維模型，槍管、彈頭和彈帽均選用八節點六面體減縮積分單元(C3D8R)，避免單元剪切閉鎖，且單元形狀對計算精度影響較小。借助有限元前處理軟件HyperMesh進行網格劃分，并開展有限元模型的網格無關性驗證。

網格劃分過程中，槍管坡膛部分對擠進過程影響較大，對其進行網格加密處理。彈頭圓柱部作為擠進膛線變形的主要部位，將其沿膛線螺旋方向劃分網格和加密。選取不同單元尺寸對模型進行網格劃分，進行網格無關性驗證。為保證計算精度并平衡計算時間，模型劃分網格總數為98.3萬個。其中槍管劃分422 840個單元格，彈帽劃分163 180個單元格，被甲劃分262 260個單元格，鉛套劃分71 280個單元格，鋼芯劃分64 000個單元格，有限元網格模型如圖3所示。采用Abaqus軟件的動態顯式算法，通過單點積分和基于黏性的沙漏控制，保證大變形計算速度和準確性。

圖3 有限元網格模型Fig.3 Meshed finite element model

1.3 材料模型

埋頭彈擠進有限元模型中，槍管、彈膛的材料為中碳低合金鋼30SiMn2MoVA，彈帽材料為聚醚醚酮(PEEK)，彈頭被甲、鉛套及鋼芯的材料分別為F11覆銅鋼、純鉛、碳素結構鋼Q235。擠進過程受到應變率、損傷等多種因素的影響，彈帽及彈頭產生彈塑性大變形，選用Johnson-Cook塑性模型進行描述。Johnson-Cook塑性模型中，Mises屈服應力為塑性應變、應變率和溫度相關的函數，可表示為

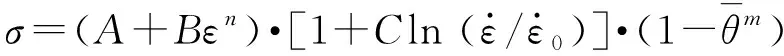
(1)

計算所用材料模型主要參數如表1所示。

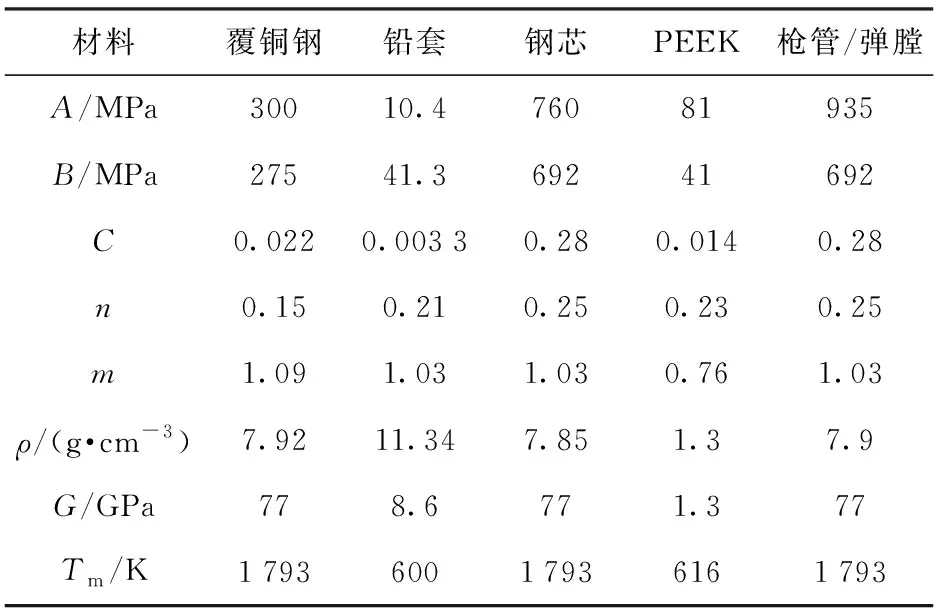
表1 材料模型參數[17-19]Table 1 Material parameters for numerical simulation[17-19]

1.4 內彈道耦合計算子程序

基于經典內彈道模型，使用Fortran語言編寫內彈道計算子程序，以4階龍格- 庫塔法求解內彈道微分方程組，獲得的膛壓值加載在彈頭底部。耦合計算時，假設彈丸啟動壓力為拔彈力，首先通過定容燃燒方程計算獲得初始相對已燃厚度、初始膛壓和彈底壓力并加載于彈底，得到彈丸運動后的位移、速度、加速度、擠進阻力、彈頭接觸應力及應變等數據，通過傳感器將數據傳回VUAMP中，子程序求解得到新的相對已燃厚度、膛壓和彈底壓力等，再回傳到Abaqus求解器再次計算彈頭運動狀態，重復上述步驟直至彈頭飛離槍口。內彈道計算基本參數如表2所示，耦合計算流程如圖4所示。

圖4 計算流程示意圖Fig.4 Schematic diagram of the calculation process

表2 內彈道計算基本參數Table 2 Parameters for internal ballistic calculations

1.5 接觸設置和邊界條件

有限元模型中彈頭被甲外表面與彈帽和槍管內膛之間、被甲內表面與鉛套之間、鉛套與鋼芯之間采用通用接觸，彈帽外表面及槍管尾端定義為完全約束，約束其全部自由度。

考慮材料的極限剪切應力與摩擦剪應力之間的關系，埋頭彈- 槍系統擠進過程采用修正的庫倫摩擦模型定義彈頭被甲與彈帽、槍管之間的摩擦。

2 模型驗證

為驗證有限元模型的正確性，設計并加工埋頭彈彈道槍和試驗用埋頭彈分別如圖5、圖6所示。圖5中整體式彈道槍彈膛與線膛一體相連，保證較好的同軸度，分體式彈道槍彈膛與線膛分開，可通過定位螺釘、墊片等部件調節彈膛位置和閉鎖間隙，用以模擬擺膛結構埋頭彈- 槍的彈/線膛不同軸現象。模型驗證試驗采用整體式測壓彈道槍進行測試，彈/線膛同軸度公差控制在0.1 mm以內。為消除彈殼對埋頭彈內彈道過程的影響，保證試驗結果的可靠性，試驗用埋頭彈采用金屬彈殼，通過尺寸測量優選將彈帽與彈膛間隙控制為0.04～0.06 mm。采用電測法測量內彈道膛壓曲線，采用光電靶測量彈頭初速。壓力傳感器(Kistler 6215，量程600 MPa，線性度誤差0.45%)安裝于距膛底16 mm位置以獲得彈殼體部膛壓，光電靶在距離膛口2 m處測量彈頭速度，采用經驗公式換算得到膛口初速。試驗共進行5次，計算最大膛壓及膛口初速的均值，并與仿真值進行對比。

圖5 埋頭彈彈道槍Fig.5 Cased telescoped ammunition

圖6 試驗用埋頭彈Fig.6 Cased telescoped ammunition for experiments

圖7為數值模擬獲得的膛壓曲線與試驗值對比，兩者極值與變化趨勢符合較好，表明計算模型的膛壓加載具有合理性。表3給出了最大膛壓和彈頭初速的仿真結果與試驗結果對比，試驗均值為5次測試結果的平均值，最大膛壓相對誤差為4.76%，膛口初速相對誤差為2.72%，均小于5 %。通過對比可知，最大膛壓與膛口初速的仿真結果與試驗值誤差較小，一致性較好，驗證了耦合計算內彈道模型的正確性。

圖7 膛壓曲線仿真與試驗結果對比Fig.7 Comparison of pressure-time curves obtained from simulation and experiment

表3 最大膛壓、初速仿真與試驗結果對比Table 3 Comparison of the maximum pressure and muzzle velocity obtained from simulation and experiment

為描述彈頭膛口姿態，引入速度坐標系和彈體坐標系，如圖8所示。圖8中，軸正向為彈頭速度方向，軸為彈體幾何軸線，俯仰角為彈軸在平面上的投影與軸的夾角，偏航角為彈軸與平面的夾角，′為軸在平面的投影。

圖8 彈頭姿態角定義Fig.8 Definition of the projectile’s attitude angle

數值模擬獲得的彈丸膛口姿態如圖9所示(彈膛偏移量為0.4 mm)，由于試驗條件限制，未能開展彈頭膛口運動的高速攝像試驗，本文借助文獻[12]中高速攝像試驗獲得的彈頭膛口姿態作為對照(彈膛偏移量為0.38 mm)，如圖10所示。對比可知，在較大的彈膛偏移量下，仿真和試驗給出的彈頭外形均發生一定程度的翹曲，彈頭膛口姿態均產生了較大的俯仰角和偏航角。兩者現象符合較好，進一步驗證了有限元計算模型的正確性。由于有限元模型未考慮膛口流場對彈頭姿態的影響，彈頭膛口俯仰角和偏航角的仿真值均小于試驗值。

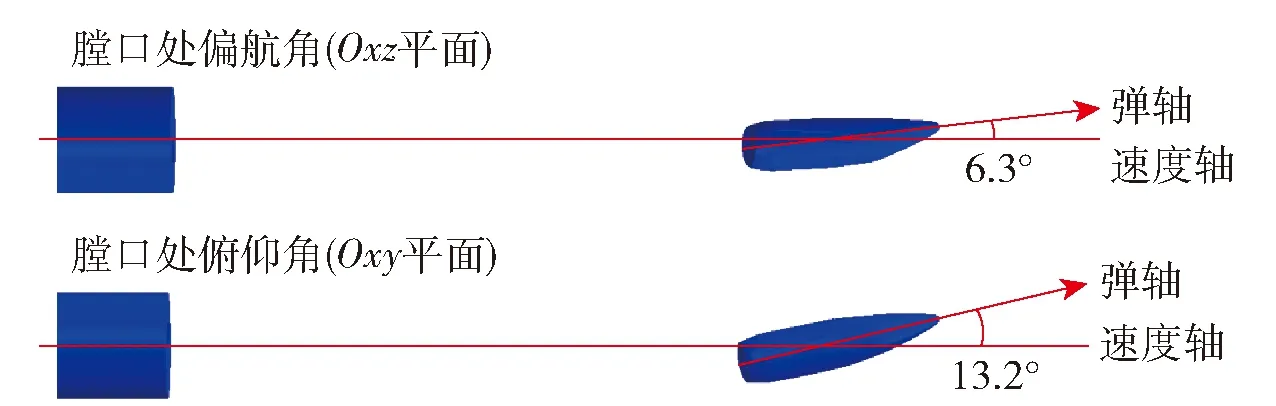
圖9 數值模擬獲得的彈頭膛口姿態Fig.9 Muzzle attitude of projectile from simulation

圖10 高速攝像獲得的彈頭膛口姿態[12]Fig.10 Muzzle attitude of projectile by high-speed photography[12]

3 仿真結果分析

3.1 彈膛偏移量對彈頭膛內運動姿態的影響

為研究彈膛偏移量對彈頭膛內運動姿態的影響，在0～0.5 mm范圍內，間隔0.1 mm，選取不同的彈膛偏移量建立埋頭彈擠進有限元模型，共6個算例，并開展數值模擬研究。圖11給出了0～0.5 mm 彈膛偏移量下彈頭擠進過程的應力云圖。由圖11 可知:隨著彈膛偏移量的增加，彈頭的接觸應力及外形翹曲程度均有大幅度增加；0～0.2 mm彈膛偏移量下，彈頭外形可較好地保持，圓柱部刻痕清晰，接觸應力分布均勻，可見在彈膛偏移量較小時，坡膛對彈頭有較好的歸正作用；0.3～0.5 mm彈膛偏移量下，彈頭外形發生較大形變，且單側出現應力集中區域。隨著彈膛偏移量的增大，彈頭表面接觸應力的急劇增加及應力分布的不均會導致坡膛處快速磨損，降低身管壽命。

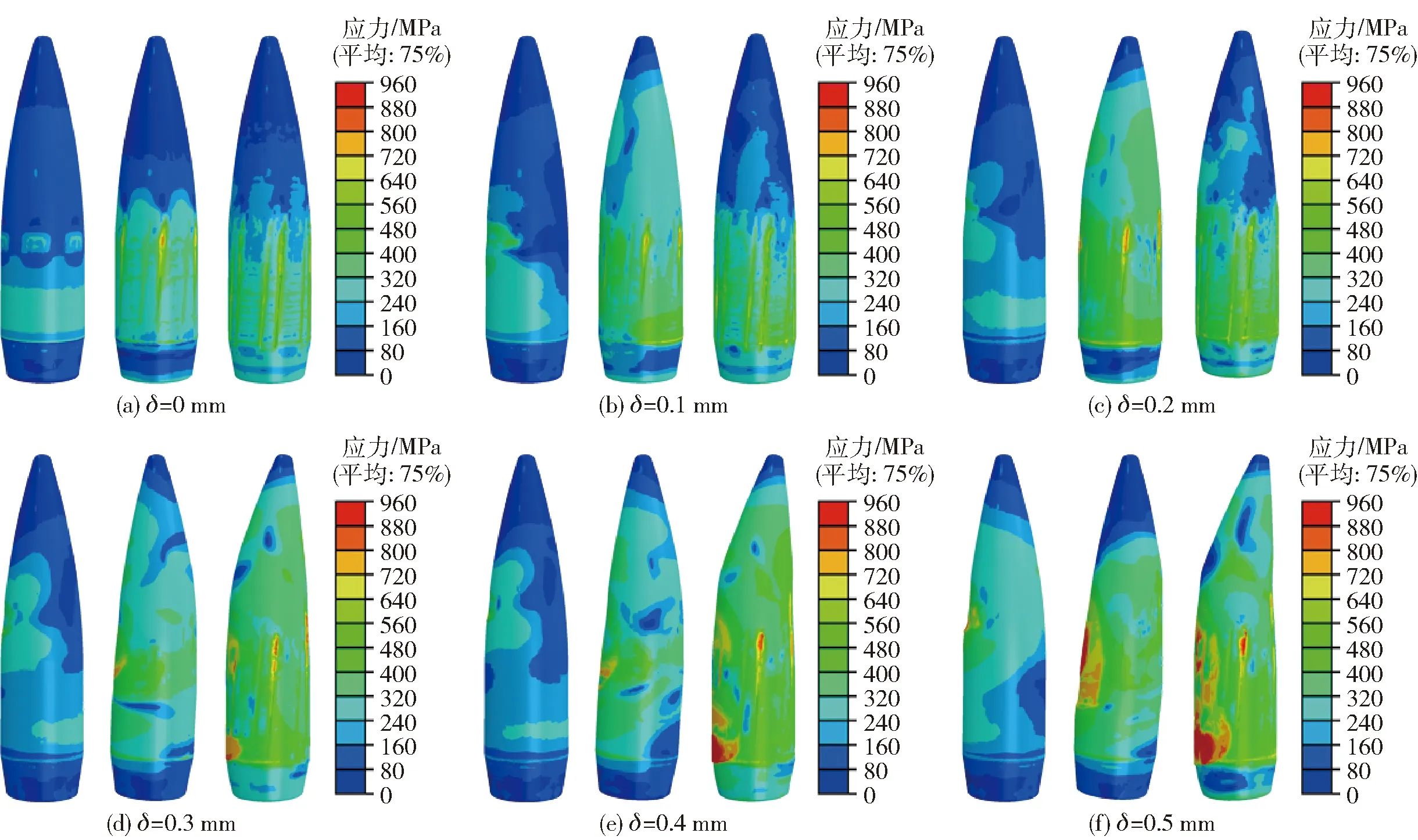
圖11 不同彈膛偏移量下彈頭的擠進過程Fig.11 Engraving process of projectiles at different chamber offsets

選擇彈頭質心偏量和膛內偏角作為表征彈頭膛內運動姿態的關鍵參量，以分析彈膛偏移量的影響。彈頭質心偏量為彈頭質心偏離線膛軸線的距離，彈頭偏角為彈頭軸線與線膛軸線之間的夾角。圖12給出了彈頭偏角、質心偏量與線膛軸線之間的關系。

圖12 彈頭偏角和質心偏量示意圖Fig.12 Schematic diagram of the projectile’s deflection angle and centroid offset

圖13為不同彈膛偏移量下彈頭的質心位置變化，各工況下初始質心偏量與彈膛偏移量相等。由圖13可知，隨著彈頭向線膛擠進，在坡膛的歸正作用下，質心位置向線膛軸線移動，在擠進過程中(17～35 mm)出現了多次振蕩，擠進結束后趨于穩定。隨著彈膛偏移量的增大，擠進結束后彈頭質心偏量也逐漸增大。圖14給出了彈膛偏移量對彈頭質心位置和膛口側向速度的影響，膛口側向速度受多種因素影響，與彈頭質心偏量呈正相關，在此不展開分析。由圖14可知：當彈膛偏移量在0～0.3 mm內增加時，彈頭擠進結束時刻的質心偏量隨著彈膛偏移量的增加而小幅增大；當彈膛偏移量大于 0.3 mm 時，彈頭質心偏量隨著彈膛偏移量的增加而急劇增大，0.5 mm彈膛偏移量下的彈頭質心偏量比 0.2 mm 工況增加約8.2倍。對照圖11中彈頭擠進后的形貌可知，彈膛偏移量較大時，彈頭外形發生較大程度形變是質心偏量急劇增大的主要原因。

圖13 不同彈膛偏移量下彈頭的質心偏量Fig.13 Centroid offsets at different chamber offsets

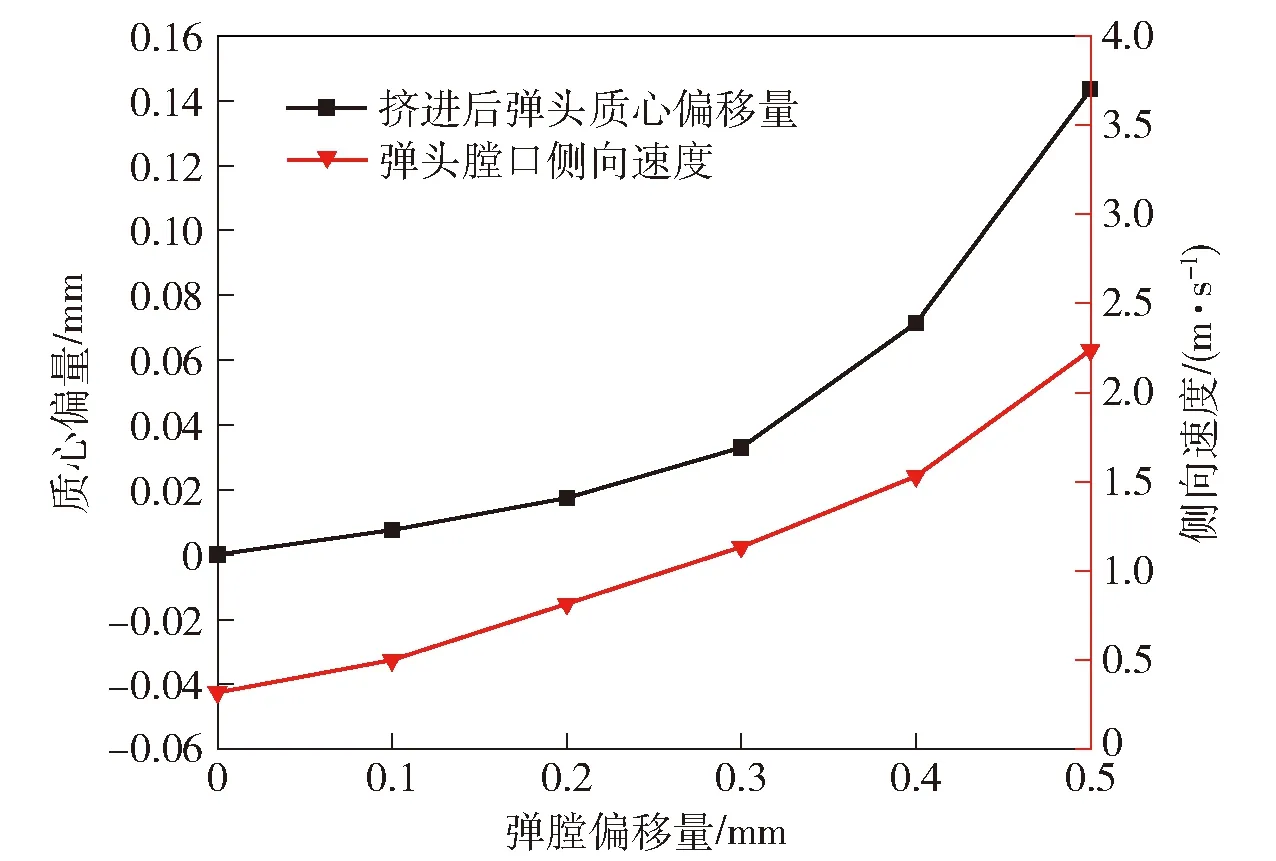
圖14 彈膛偏移量對彈頭質心偏量和膛口側向速度的影響Fig.14 Effect of chamber offset on centroid offset and muzzle lateral velocity

圖15為不同彈膛偏移量下彈頭的膛內偏角變化。由圖15可知，隨著彈頭向線膛擠進，彈頭膛內偏角快速增大后略微減小，在擠進完成后趨于穩定。隨著彈膛偏移量的增大，擠進結束后彈頭偏角也逐漸增大，0.5 mm彈膛偏移量下的彈頭偏角比0.2 mm工況增加約3.8倍。選定擠進結束時刻(位移為 35 mm)和彈頭出膛時刻作為考察點，給出彈膛偏移量對彈頭偏角的影響如圖16所示。由圖16可見，各工況下出膛瞬間的彈膛偏角比擠進結束時刻均略微增大，出膛瞬間的彈膛偏角約為擠進結束時刻的1.27倍。中間彈道研究表明，初始攻角在1°～3°之間時，在陀螺穩定作用下，彈頭可保持較好的飛行姿態，而較大的初始攻角會導致外彈道穩定性下降。由圖15可知，當彈膛偏移量為0.3～ 0.5 mm 時，擠進結束位置和膛口位置的彈頭偏角均大于3°，這對保持外彈道飛行穩定性及射擊精度是不利的。

圖15 不同彈膛偏移量下彈頭的膛內偏角Fig.15 Deflection angles at different chamber offsets

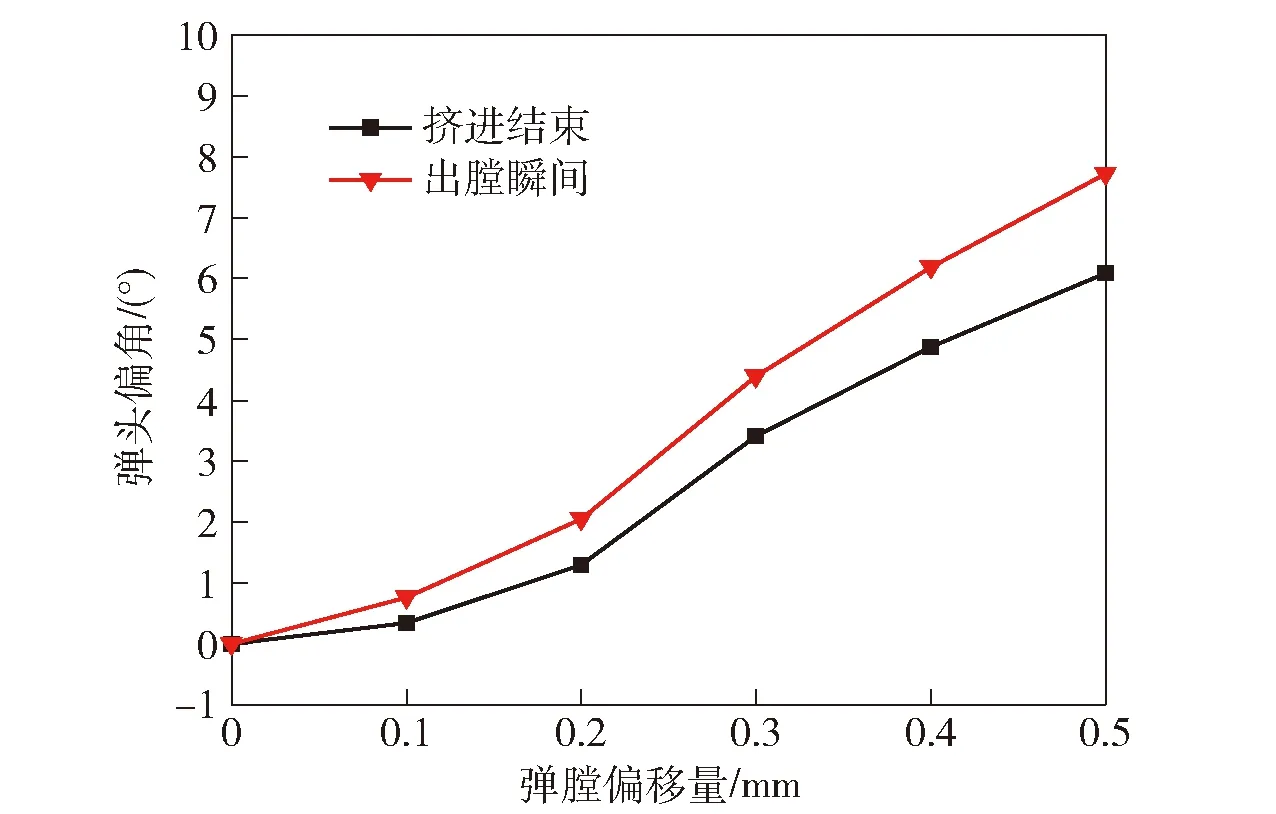
圖16 彈膛偏移量對彈頭偏角的影響Fig.16 Effect of chamber offset on deflection angle

3.2 彈膛偏移量對內彈道特性的影響

彈膛偏移量對內彈道特性的影響主要體現在擠進阻力、擠進速度、最大膛壓及彈頭初速4個方面。不同彈膛偏移量下彈頭的擠進阻力如圖17所示。彈膛與線膛完全對中時(彈膛偏移量為0 mm)，擠進阻力在位移為26 mm時達到最大值(圖示峰值3)，此時彈頭圓柱部完全嵌入坡膛。當存在彈膛偏移量時，擠進阻力在圓柱部完全嵌入坡膛前會出現兩個峰值(圖示峰值1、峰值2)，且隨著彈膛偏移量的增大，這兩個峰值也顯著增大。

圖17 不同彈膛偏移量下彈頭的擠進阻力Fig.17 Engraving resistance levels at different chamber offsets

通過埋頭彈擠進過程示意圖，分析擠進阻力多個峰值產生的原因，如圖18所示。初始狀態下(見圖18(a))，彈膛軸與線膛軸之間存在偏移量，即彈軸與線膛軸存在不同軸現象。彈頭底部受火藥燃氣推動，在彈帽內孔的導向作用下向前運動，由于彈軸與線膛不同軸，彈頭與坡膛接觸位置發生偏移，產生第1次碰撞(見圖18(b))，由此產生擠進阻力曲線中的峰值1。彈頭在火藥燃氣推動、彈帽約束和坡膛導向三者共同作用下繼續向前運動并產生膛內偏角，彈頭在第1次碰撞的對側與坡膛產生第2次碰撞(見圖18(c))，由此產生擠進阻力曲線中的峰值2。在此之后，彈頭繼續向前運動脫離彈帽，圓柱部完全嵌入坡膛(見圖18(d))，產生擠進阻力曲線中的峰值3。最終彈頭完全嵌入線膛(見圖18(e))，擠進阻力趨于穩定，最終的擠進阻力主要體現為彈頭與線膛之間的滑動摩擦力。

圖18 埋頭彈擠進過程示意圖Fig.18 Schematic diagram of the engraving process of the cased telescoped ammunition

圖19給出了彈膛偏移量對彈頭擠進阻力3個峰值的影響。由圖19可知：擠進阻力峰值1和峰值2均隨著彈膛偏移量的增加而快速增大，而不同彈膛偏移量下的峰值3基本相等；彈膛偏移量達到 0.5 mm 時，峰值1與峰值3基本相當；彈膛偏移量大于0.2 mm后，峰值2超越峰值3，成為最大擠進阻力；0.5 mm彈膛偏移量下，峰值2約為峰值3的2.2倍。擠進阻力的顯著增大表明槍管坡膛處接觸應力的增大，會導致槍管加速磨損失效和鍍層剝落現象，降低槍管使用壽命。

圖19 彈膛偏移量對彈頭擠進阻力的影響Fig.19 Effect of chamber offset on engraving resistance

圖20為不同彈膛偏移量下彈頭的擠進速度隨位移變化的曲線，圖21為彈膛偏移量對最大膛壓及初速的影響。由圖20和圖21可知，由于彈膛偏移量的增加帶來了擠進阻力的顯著增大，進而導致擠進速度的略微降低、最大膛壓的急劇升高，以及彈頭初速的提高。相較于完全對中工況，彈膛偏差為0.5 mm時，擠進結束時刻的彈頭速度由313.2 m/s降低至290.2 m/s，降低了7.3%，最大膛壓由289.6 MPa升高至328.2 MPa，提高了13.3%，彈頭初速由826.5 m/s升高至856.7 m/s，提高了3.7%。其中，最大膛壓的顯著升高對武器系統的安全性帶來嚴重危害。

圖20 不同彈膛偏移量下彈頭的擠進速度Fig.20 Engraving velocities at different chamber offsets

圖21 彈膛偏移量對最大膛壓及初速的影響Fig.21 Effect of chamber offset on maximum pressure and muzzle velocity

4 彈帽結構優化設計

4.1 彈帽關鍵參量

彈膛偏移量的存在對埋頭彈- 槍系統的精度、壽命及安全性均有不利影響，因此有必要開展埋頭彈結構優化設計，以降低彈/線膛不對中現象帶來的危害。作為參與彈頭擠進階段相互作用的主要部件，彈帽的結構優化顯得尤為重要。選取彈帽內孔直徑和倒角深度為結構優化的關鍵參量，如圖22所示。考慮彈頭外形尺寸及各部件配合關系，彈帽內孔直徑優化范圍設定為5.8～6.0 mm，步長為 0.05 mm，共5個尺寸，倒角深度優化范圍設定為1.2～3.6 mm，步長為0.2 mm，共13個尺寸，選取0.3 mm彈膛偏移量作為優化工況，分別劃分網格，建立不同彈帽結構尺寸的埋頭彈擠進有限元模型，共計65個數值仿真算例，并分析彈帽結構參量對彈頭質心偏量、膛內偏角及擠進阻力3個關鍵因素的影響。

圖22 彈帽關鍵參量示意圖Fig.22 Key parameters of the projectile cap

4.2 彈帽結構對彈丸運動姿態及擠進阻力的影響

圖23為彈帽結構對彈頭質心偏量的影響。由圖23可知：彈頭質心偏量隨著彈帽倒角深度的增大呈現先減小后增大的變化趨勢，在倒角深度為 2.0～2.4 mm時出現最小值，相較于1.2 mm的初始尺寸，質心偏量降低約0.038 mm；彈頭質心偏量對彈帽內孔直徑的變化不敏感，隨著內孔直徑的增大，質量偏心略微減小；倒角深度為2.2 mm時，6.0 mm內孔直徑對應的彈頭偏角比5.8 mm工況減小了0.009 4 mm。圖24為彈帽結構對彈頭膛內偏角的影響。由圖24可知：彈頭偏角隨著彈帽倒角深度的增大逐漸減小，3.6 mm倒角深度對應的彈頭偏角比1.2 mm工況減小約1.4°；彈頭偏角隨彈帽內孔直徑的增大而略微減小，倒角深度為2.2 mm時，6.0 mm 內孔直徑對應的彈頭偏角比5.8 mm工況減小了0.43°。圖25為彈帽結構對彈頭最大擠進阻力的影響，由圖25可知，在內孔直徑為5.8 mm和5.85 mm工況下，最大擠進阻力帽倒角深度的增大而逐漸減小，而在5.9～6.0 mm內孔直徑工況下，最大擠進阻力隨倒角深度的增大出現先減小后增大再減小的波浪形趨勢，在2.2 mm位置出現極小值。

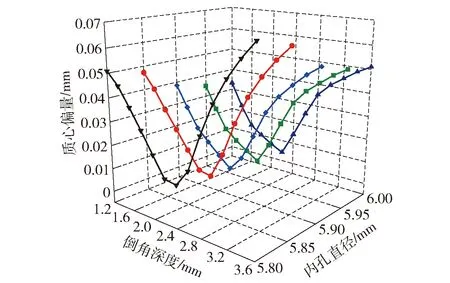
圖23 彈帽結構對彈頭質心偏量的影響Fig.23 Effect of the structure of the projectile cap on centroid offset

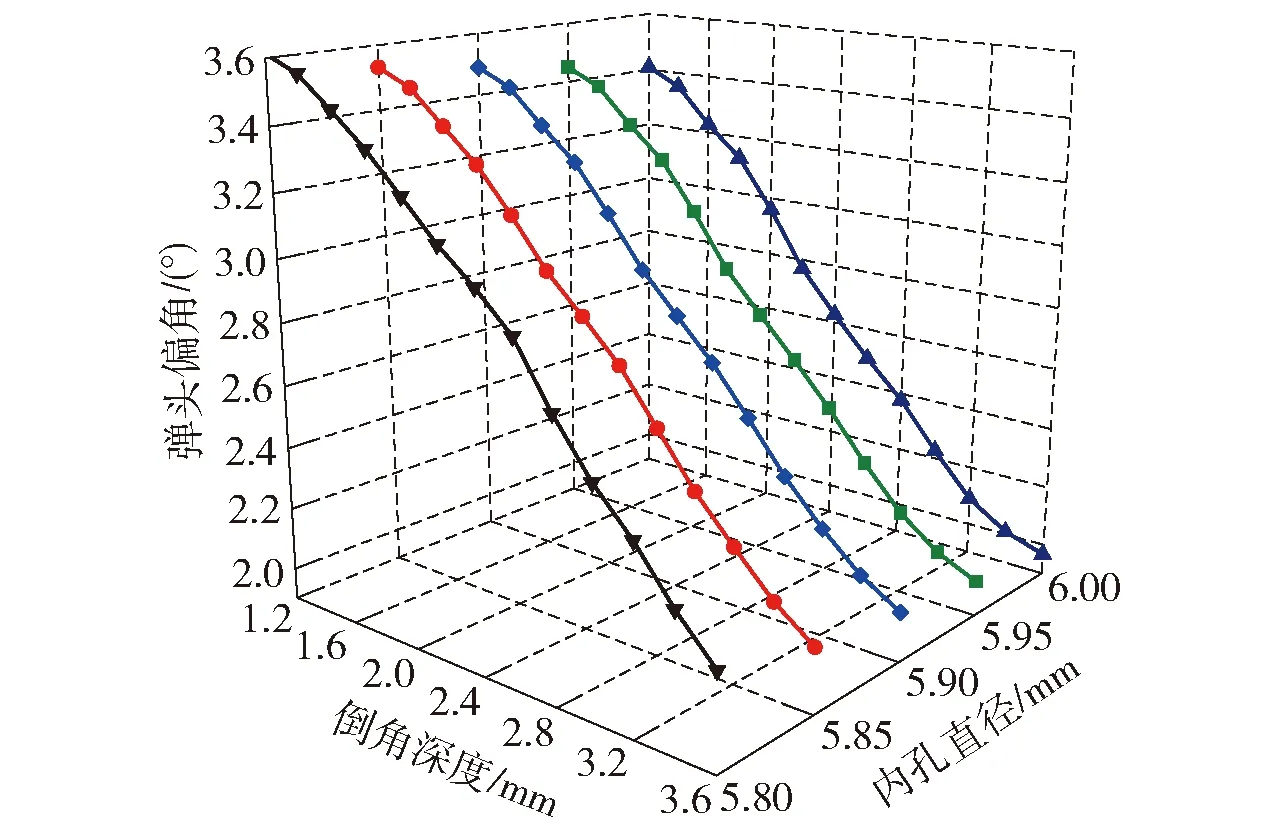
圖24 彈帽結構對擠進結束時刻彈頭偏角的影響Fig.24 Effect of the structure of the projectile cap on deflection angle after engraved

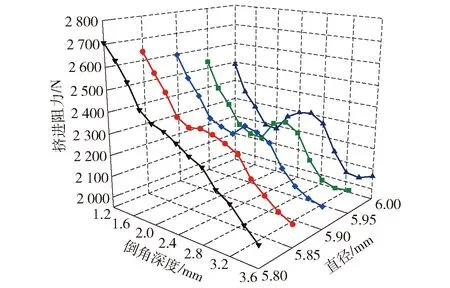
圖25 彈帽結構對彈頭最大擠進阻力的影響Fig.25 Effect of the structure of the projectile cap on maximum engraving resistance

分析彈帽及坡膛對彈頭的約束關系發現，當彈帽倒角深度在2.0～2.4 mm時，彈帽與坡膛可較好地共同約束彈頭向前運動。而倒角深度大于 2.4 mm 時，彈頭前進過程中會出現單側約束的現象，即當彈頭脫離彈帽約束后仍未能較好地嵌入坡膛，彈頭運動失穩導致質心偏量的增大，此時坡膛可對彈頭發揮較強的歸正作用，因此出現彈頭偏角繼續減小的現象。這種不連續約束也會導致火藥燃氣泄漏現象，降低內彈道效率，在彈帽設計中應避免出現。

4.3 彈帽結構優化前后對比

根據數值模擬結果，綜合考慮3種因素的作用對彈帽結構參量進行優選，內孔直徑5.95 mm，倒角深度2.2 mm的工況為較好的選擇。選擇內孔直徑5.80 mm、倒角深度1.2 mm為初始狀態對照組。圖26為彈帽優化前后彈頭的變形情況對比，由圖26 可知，優化后的彈頭翹曲程度降低，彈頭表面最大應力值減小，應力分布較為均勻，沒有單側應力集中現象。表4給出了彈帽結構優化前后各因素的對比情況，可見優化后的結構方案可大幅度降低彈頭質心偏量，且彈頭偏角和最大擠進阻力也有較好的改善。

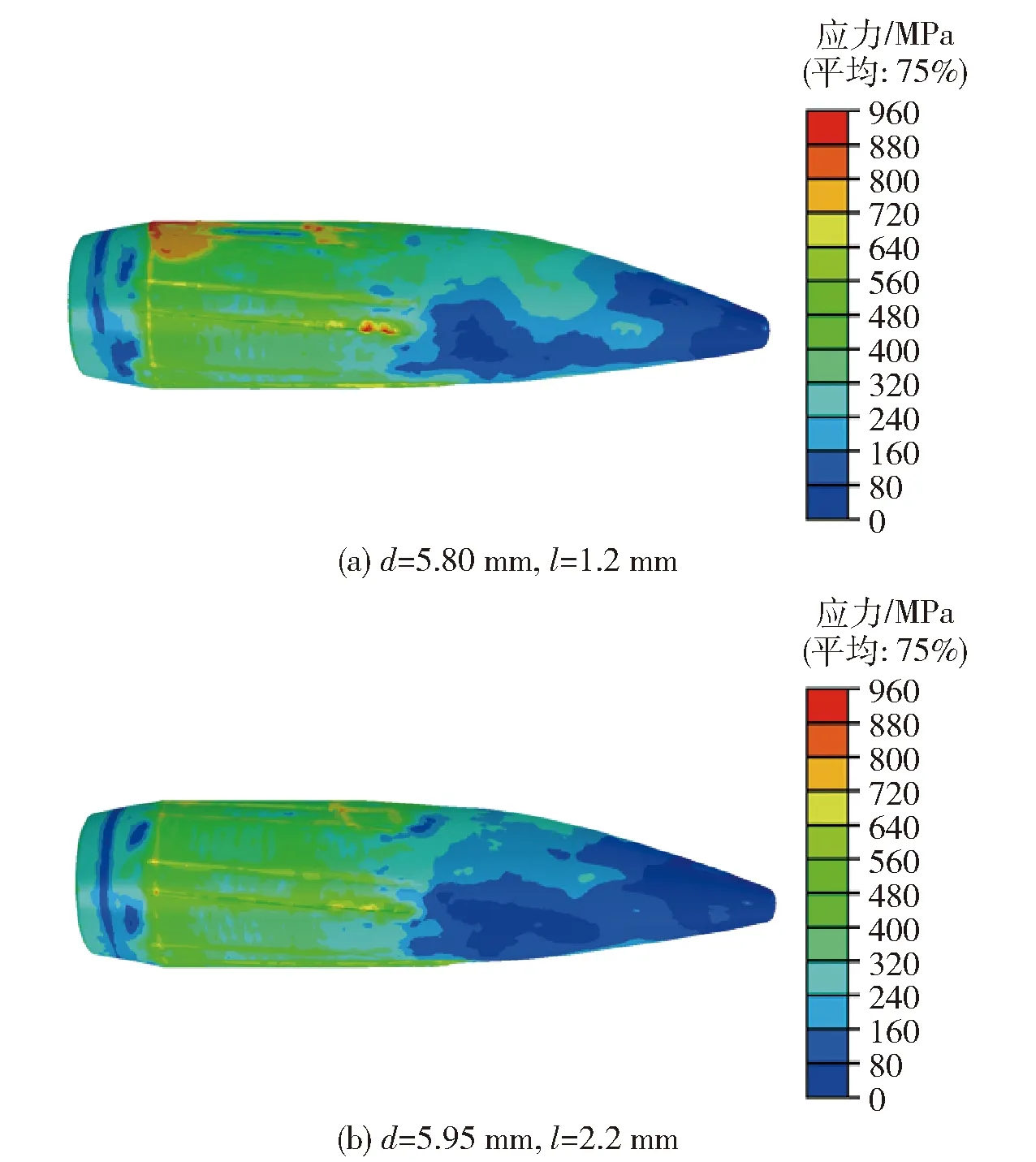
圖26 彈帽優化前(a)后(b)彈頭的變形情況對比Fig.26 Comparison of projectile deformation before (a) and after (b) cap structure optimization

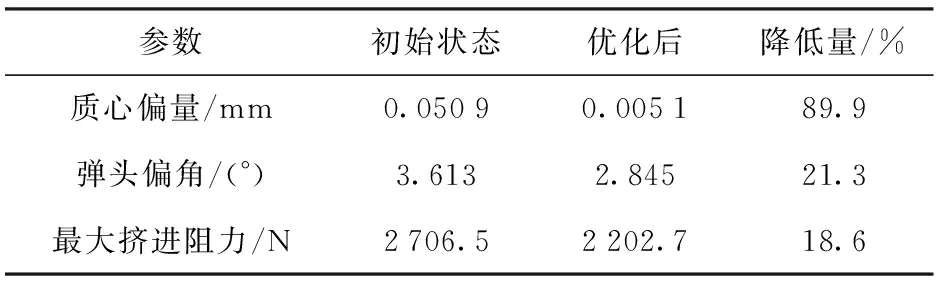
表4 彈帽結構優化前后各因素對比Table 4 Key parameters before and after cap structure optimization

4.4 優化方案驗證

彈帽結構優化的驗證試驗采用分體式測速彈道槍開展。彈道槍的最大彈膛偏移量約為0.3～0.4 mm，閉鎖間隙約為0～0.1 mm。對照組彈帽內孔直徑為5.8 mm±0.05 mm，倒角深度為1.2 mm±0.1 mm，優化后彈帽內孔直徑為5.95 mm±0.05 mm，倒角深度為2.2 mm±0.1 mm。試驗分為姿態測量試驗和精度試驗，采用紙靶法測量2 m處彈孔情況以考察彈頭的膛口姿態，采用100 m精度試驗考察埋頭彈射擊精度。

姿態測量試驗獲得的彈孔如圖27所示。由圖27可知，彈帽結構優化前出現了橢圓彈孔現象，測量得到彈孔長軸均值為12.13 mm，計算可得平均彈頭偏角為22.4°，該工況下彈頭膛口姿態較差，在外彈道飛行過程中可能會發生失穩，甚至翻滾現象。而彈帽結構優化后的彈孔基本圓正，表明該工況下彈頭有較好的外彈道飛行姿態。姿態測量試驗表明，彈帽結構優化后的埋頭彈在射擊時有較好的外彈道飛行穩定性。

圖27 彈帽結構優化前后的彈孔對比Fig.27 Comparison of projectile holes before and after cap structure optimization

精度試驗中，兩種彈帽結構的埋頭彈分別進行3組射擊試驗，每組射彈10發，射擊結束后通過測量靶紙收集的彈孔計算3組精度試驗50和100的平均值。試驗設置對照組，采用整體式測速彈道槍(彈/線膛偏差小于0.1 mm)作為無彈膛偏移量的射擊條件，射擊彈帽結構優化前的埋頭彈，進行3組精度試驗，并計算50和100的平均值。

試驗獲得精度數據如表5所示。對比可知，彈帽結構優化后埋頭彈的精度得到了有效提高，已接近無彈膛偏移量工況下的射擊精度。圖28為彈帽優化后100 m處的彈孔情況，圖示彈孔圓正，可推斷彈帽優化后的埋頭彈在較大的彈膛偏移量下(0.3～0.4 mm)仍保持較好的外彈道飛行姿態。姿態測量試驗和精度試驗驗證了彈帽優化方案的有效性。

表5 彈帽結構優化前后100 m射擊精度對比Table 5 Comparison of shooting accuracies from 100 m before and after cap structure optimization

圖28 彈帽結構優化后的100 m精度Fig.28 Projectile dispersion after shooting from 100 m with an optimized cap structure

5 結論

本文為研究彈膛偏移對埋頭彈擠進過程的影響，通過數值模擬和試驗研究相結合的方法開展埋頭彈動態擠進研究。采用顯式動力學方法并耦合內彈道方程，建立了埋頭彈擠進過程的彈- 槍相互作用有限元模型，通過數值模擬分析了彈膛偏移量對彈頭質心偏量、膛內偏角及擠進阻力等因素的影響，并開展了彈帽結構優化設計。得出以下主要結論：

1)數值模擬得到的膛壓曲線與試驗測試值一致性較好，最大膛壓和膛口初速誤差均小于5%，彈頭出膛后的表面形貌及飛行姿態與文獻[12]中的試驗數據相符，驗證了數值模型的可靠性。

2)在0～0.5 mm范圍內，隨著彈膛偏移量的增大，擠進結束時刻彈頭的質心偏量、膛內偏角及最大擠進阻力均有不同程度的增大，導致彈頭翹曲變形、彈頭外彈道飛行失穩、最大膛壓顯著升高、坡膛加速磨損失效等現象。彈/線膛不同軸對埋頭彈- 槍系統的精度、壽命及安全性均有不利影響。

3)彈帽關鍵結構參量中，內孔倒角深度對彈頭質心偏量、膛內偏角及最大擠進阻力影響較為顯著，通過結構優化設計可大幅度降低彈頭質心偏量，且彈頭偏角和最大擠進阻力也有明顯改善。

4)姿態測量試驗和精度試驗驗證了彈帽優化方案的有效性，經結構優化后的彈帽可保證彈頭外彈道飛行穩定性，并提高射擊精度。