分段桿彈的梯度化設計

喻爭， 王舒， 董方棟， 鄭志軍， 崔世堂， 張永亮,

(1.中國科學技術大學 近代力學系 中國科學院材料力學行為和設計重點實驗室， 安徽 合肥 230026;2.中國兵器工業第208研究所 瞬態沖擊技術重點實驗室， 北京 102202)

0 引言

隨著裝甲的不斷升級，普通穿甲彈對裝甲的侵徹破壞能力日漸式微。動能武器，尤其是長桿彈逐漸成為了近年來兵器領域研究的熱點。但由于發射條件的限制，不斷提高長徑比以增加長桿彈侵徹深度的方式逐漸失效。20世紀80年代，有學者提出了分段桿彈的概念。分段桿彈是指將長桿彈彈體人為分為長徑比較小的獨立彈體的一種新型彈藥形式。文獻[1-3]研究結果表明，在相同的質量下，分段桿彈侵徹效率高于長桿彈。如何發揮出分段桿彈最大的侵徹效能成為研究的熱點問題。

實驗方面，Cuadros對帶鋁套筒的鎢合金分段桿侵徹裝甲鋼進行了速度2～4 km/s的彈道實驗，結果表明在1～3倍彈徑范圍內增大各段之間的間隔可增大分段桿侵徹深度。Sorensen等的實驗結果證明，在分段桿彈各段之間填充玻璃纖維會降低侵徹效率。Franzen實驗證明在相同質量、直徑、速度和總長度條件下不斷減小各段長徑比并不能無限提高侵徹深度。Wang等實驗研究了鋁套筒對分段桿彈侵徹的影響，發現套筒對侵徹深度有一定貢獻。隨著數值模擬技術的發展，對分段桿彈的研究逐漸深入。Normandia等利用軸對稱模型計算了速度2.6 km/s下長徑比小于1的分段桿彈對半無限鋼靶的侵徹過程，表明前段殘留物會減小后段侵徹效率，通過技術手段去除殘留物可以進一步提高分段桿彈侵徹深度。Tate提出了簡化模型以評估前段殘留物對后段彈體侵徹的影響，并據此優化了分段桿各段之間間隔從而提高分段桿侵徹能力。Littlefield和Lee研究了斜置分段桿彈對斜置分層靶板的侵徹，發現合理斜置分段桿可以提高侵徹深度。Jo等研究了相同的問題，發現增加分段之間間隔和各段長度可以提高分段桿對分層靶板的侵徹深度。朗林等、胡靜等、鄧云飛等、Cao等用光滑粒子算法研究了不同連接形式對分段桿侵徹深度的貢獻。蔣建偉等研究了分段數目、間隔等對侵徹深度的影響，特別研究了不同形狀頭部對侵徹的影響，發現尖錐形、球形和截錐形頭部均優于圓柱形頭部。陳建良等研究了鎢纖維對分段桿侵徹性能的增強效應。由此可見對分段桿彈的研究集中在最優長徑比、最優分段間隔、彈體形狀、材料等方面，但在實際應用中，分段桿彈之間的間隔會造成彈體過長，造成分段桿彈的發射困難以及侵徹過程中的不同軸。因此在保證侵徹深度的前提下盡可能減小長度是分段桿彈研究設計的重要目標之一。梯度化是對彈體結構優化設計的可行手段。但目前關于分段桿彈的梯度化設計研究較為匱乏。2019年，焦文俊等總結了分段桿彈侵徹的相關研究進展，建議繼續對分段桿彈開展實驗、模擬和理論研究，并提出要分析變密度(梯度變化或周期變化)桿等新彈體構型的侵徹性能。

本文分別構造了長度和直徑梯度變化的分段桿彈，采用數值模擬方法對比研究了其侵徹效率，并對計算結果進行了理論分析。

1 侵徹過程數值模擬

1.1 參照實驗

本文參照Charters等開展的實驗進行數值模擬研究，對照其實驗結果驗證有限元模型的有效性。實驗長桿彈結構如圖1所示。

圖1 長桿彈Fig.1 The long rod the segmented rod projectile

實驗中的彈體為鎢合金材料(鎢鎳鐵合金)，靶體為RHA(4340)鋼。所述長桿彈彈體為均質圓柱形，直徑為5.54 mm，長徑比5；靶體尺寸為200 mm×200 mm。實驗采用輕氣炮發射，實驗速度范圍2.0～4.0 km/s。

1.2 有限元模型

對長桿彈、理想分段桿彈和靶板進行建模，考慮到研究對象具有對稱性，采用1/4對稱模型以縮短計算時間。長桿彈總尺寸5.54 mm×27.7 mm；考慮到求解規模，將靶板尺寸設置為70 mm×100 mm。經網格收斂性分析，模型求解結果隨著網格變小收斂，考慮求解效率，確定網格大小為0.33 mm×0.33 mm。靶板靠近對稱軸10 mm內單元尺寸為0.33 mm×0.33 mm，沿半徑方向過渡。采用TrueGrid軟件進行映射網格劃分。彈、靶均采用3D solid164實體單元，總單元數245 840。彈、靶的對稱界面采用對稱約束，靶板下方界面采用全約束，外邊界采用無反射邊界以消除反射應力波的影響。彈、靶有限元模型如圖2所示。

圖2 有限元模型Fig.2 Finite element model of target and projectile

1.3 彈、靶材料本構模型及其參數

Johnson-Cook模型考慮了應變、溫度和應變率對屈服應力的影響，是描述金屬動態力學行為常用的本構模型，因此采用該模型描述彈體和靶體。模型數學表述為

(1)

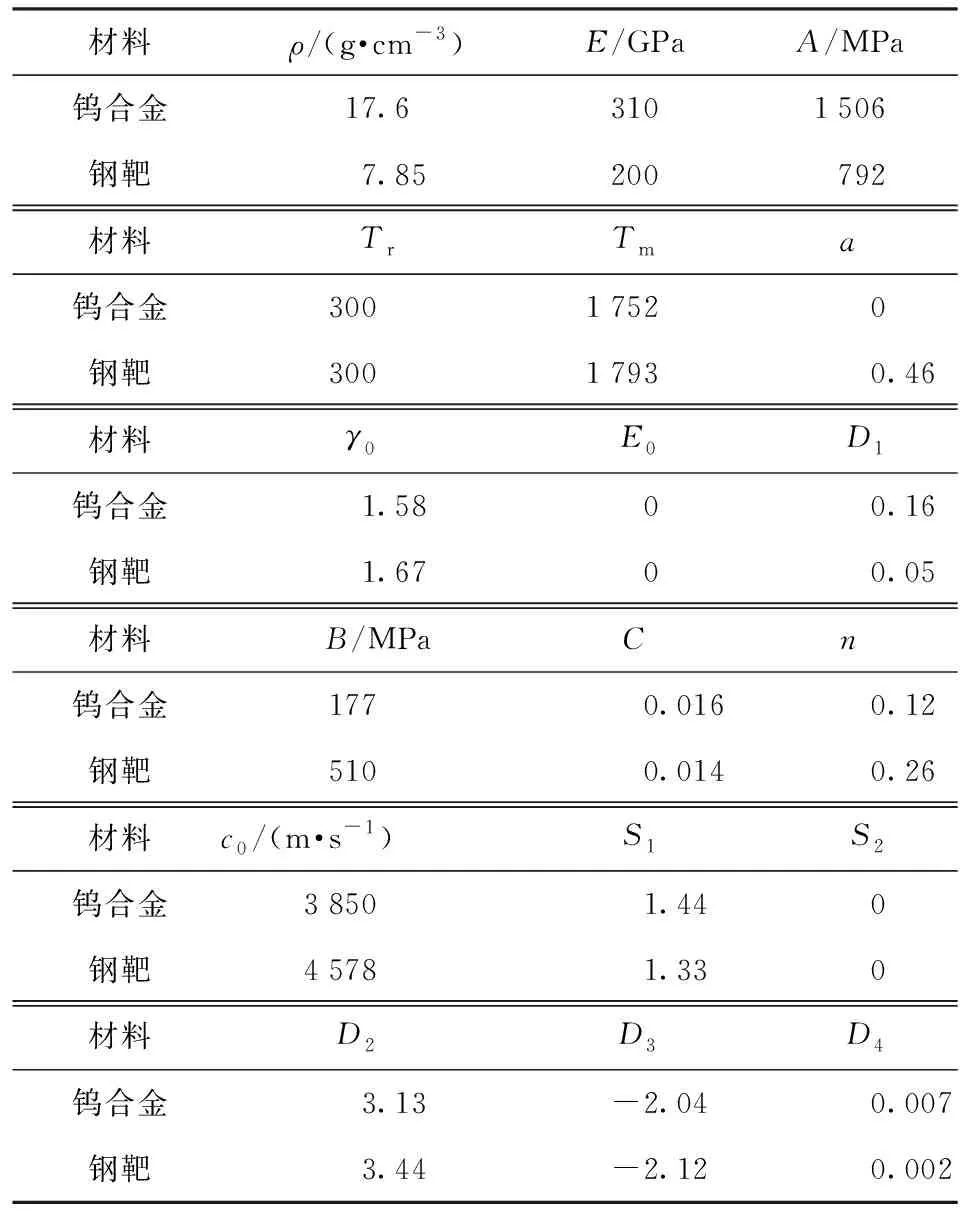
表1 彈、靶材料參數Table 1 Material parameters of target and projectile

1.4 單元刪除和接觸算法

采用Johnson-Cook材料損傷準則，即最大等效應變損傷準則。在計算時，材料超過彈性極限將產生塑性應變，當塑性應變積累到一定程度時材料損傷。數學表達式如下：

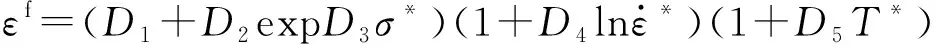
(2)

2 計算結果與實驗對比

采用12節本構模型和參數對鎢合金長桿彈侵徹鋼靶的實驗進行數值模擬。有限元計算所得侵徹深度與文獻[18]實驗結果的對比如圖3所示。

圖3 侵徹深度有限元結果與實驗結果對比Fig.3 Penetration depth FEM compared with EXP

由圖3可見，隨著速度的增大，實驗與有限元計算所得侵徹深度呈相近的增大趨勢。與計算值相比，長桿彈侵徹深度的實驗值較小，這是因為長桿彈在實際侵徹過程中不是始終正侵徹，而是會與靶板呈一定角度。

圖4給出了長桿彈侵徹過程中4個時刻的物理圖像。由圖4可見：=0 μs時刻，長桿彈以2 000 m/s的速度與靶板表面發生沖擊，產生瞬時高壓，靶板表面被擊潰；=15 μs時刻，此時長桿彈速度幾乎保持不變，進入準定常半流體侵徹階段；=30 μs時刻，剩余彈體無量綱長度約為1，靶板進入后流動階段。侵徹的最后階段，剩余彈體動能殆盡，靶板回彈。

圖4 長桿彈侵徹過程中彈體和鋼靶的有效應力分布Fig.4 Effective stress distribution of projectile and target during penetration by long-rod projectile

長桿彈侵徹的4個階段彈與靶板的接觸力呈現出不同的特點。如圖5所示，初始瞬態階段(Ⅰ)出現壓力陡峰，時間僅幾個微秒；隨后進入準定常侵徹階段(Ⅱ)，接觸反力在某一恒值附近抖動，準定常階段持續時間達25 μs左右，貢獻了長桿彈絕大部分的侵徹深度；后流動階段(Ⅲ)和靶板反彈階段(Ⅳ)接觸力逐漸下降，直至為0 kN。

圖5 彈- 靶界面接觸力有限元仿真結果Fig.5 Projectile-target interface contact force FEM

圖6為長桿彈侵徹半無限靶空腔形貌的數值模擬結果與實驗對比情況，兩者略有差異，但能夠反映鎢合金侵徹裝甲鋼的主要物理規律。總之，所構建的有限元模型及其采用的參數是可靠的，為分段桿彈的梯度化設計奠定了研究基礎。

圖6 長桿彈有限元仿真與實驗[18]空腔形貌對比Fig.6 Cavity morphology of FEM versus EXP[18]

3 分段桿梯度配置侵徹效能對比

3.1 數值計算

本文構造了正梯度、負梯度和均勻分布的5種分段桿彈，如圖7所示。所述的正梯度是指靶板法向方向上分段桿各段長度遞增；負梯度是指法向方向上分段桿各段長度遞減，均勻分布則是各段長度相等。梯度定義為前后兩段桿的長度差。構造了梯度為0 mm的均勻分段桿、梯度為1 mm和2 mm正梯度以及梯度為-1 mm和-2 mm的負梯度共5種分段桿。段與段之間的間距取為前段桿的長度。

圖7 梯度分段桿配置Fig.7 Gradient segmented rod configuration

=0 mm的均勻等長桿在速度=3 000 m/s的初速下侵徹靶板的等效應力云圖如圖8所示。由圖8可見：=6 μs時，第1段桿與靶板發生沖擊，應力波由接觸面向靶板內部傳播，靶板內部應力波陣面呈球形，在靶板界面處形成盆口；=10 μs時，第2段桿全部消蝕，第3段桿在前一段桿所形成的空腔基礎上繼續侵徹；=20 μs和=25 μs時，第3段桿和第4段桿繼續侵徹；=30 μs時整個桿全部消蝕，侵徹深度達到最大，整個侵徹空腔呈糖葫蘆串狀。

圖8 等效應力云圖Fig.8 von Mises stress contours

5種配置的分段桿在=3 000 m/s的初速下侵徹RHA半無限鋼靶的最后侵徹深度如表2所示。由表2可見：均勻分布的分段桿侵徹深度為565 mm，整體侵徹效度113，表現最優。其余結果呈現侵徹深度以=0 mm為中心，逐步降低的趨勢，且偏離值越大，侵徹深度降低得越多。

表2 梯度配置分段桿侵深Table 2 Penetration of segmented rod with different gradient configuration

分別取值為1 500 m/s、2 000 m/s和3 000 m/s的計算結果如圖9所示，從中可見侵徹深度均表現出以=0 mm為中心、逐步降低的趨勢，且偏離值越大，侵徹深度降低得越多。

圖9 不同速度下侵徹深度隨等差值的變化曲線Fig.9 Variation curve of penetration depth with equidifference at different speeds

圖10為等差配置的分段桿侵徹半無限靶后的截面。由圖10可見：所有配置的分段桿整體截面形狀都呈糖葫蘆串狀；各段所形成的空腔與長徑比呈相關，即長徑比越大，所形成的空腔越長；在彈- 靶界面處的空腔直徑明顯大于內部的空腔直徑，且各配置分段桿的彈- 靶界面空腔直徑近似相等，與長徑比無關；靶板內部，各段空腔最大直徑也近似相等，與所處位置和彈的長徑比無關。

圖10 等效塑性應變云圖Fig.10 Effective plastic strain contours

3.2 理論分析

長桿彈侵徹的長徑比效應是指隨著長徑比增加，消蝕單位長度桿所得到的侵徹深度減小。如圖11所示，速度一定時，隨著長徑比的增大，無量綱侵徹深度呈現亞線性增加趨勢。曲線斜率，即侵徹效率，隨著長徑比的增加逐漸減小。文獻[21]系統描述了長徑比效應。圖11中，為侵徹深度，為長桿彈直徑，為彈的長度。

圖11 長徑比效應Fig.11 Effect of L/D

經過擬合曲線，將長徑比效應表述為

(3)

(4)

式中：為總分段數，這里為5；為分段桿各段長度。均勻分段桿侵徹總深度可以寫為

(5)

根據廣義二項式定理可證以下不等式成立：

(6)

由此可知，固定分段桿彈直徑和總有效長度時，均勻分段時侵徹總深度最大；而等差配置或者等比配置分段桿長度均會偏離最大點，使總體侵徹深度減小。

～(1-3)

(7)

由于=077，即1-3<0，在固定各段體積時，侵徹深度將隨著直徑的減小而增大。因此可以得出結論：在彈體總體積或總質量一定時，直徑越小，長徑比越小，總侵徹深度越大。

因此，基于上述結論即可構造直徑梯度變化的分段桿彈。該分段桿彈在靶板法向方向上各段體積相等，直徑逐漸增大，長度逐漸減小，所配置的各段桿彈長度和直徑如表3所示。沿著靶板法向方向上直徑遞減，保持各段體積不變。計算結果如圖12所示。3 000 m/s的初速下侵徹半無限裝甲鋼靶最終深度為71 mm，比均勻分布長桿深度要大26，即直徑梯度配置的分段桿優于長度梯度配置的分段桿彈。

表3 變直徑梯度桿配置Table 3 Variable diameter gradient rod configuration

圖12 變直徑梯度桿及等效塑性應變云圖Fig.12 Penetration of variable diameter gradient rod

4 結論

1) 本文利用LS-DYNA拉格朗日算法模擬了鎢合金長桿彈侵徹半無限鋼靶的實驗，數值計算結果與實驗結果較為一致，證明了數值模型的有效性。

2) 構造了5種等差梯度的分段桿彈，并進行了數值模擬。長度均勻相等的分段桿侵徹效率最高，侵徹深度最大；長度梯度變化桿，桿長等差值越大，侵深越小。

3) 闡述了長徑比效應對等差梯度配置的分段桿彈侵徹深度的分段桿彈的影響規律，理論上證明了變直徑和變長徑比分段桿的可行性，并數值模擬進行了分析驗證，為分段桿彈的優化設計提供了依據。