大跨度勁性骨架拱橋Pushover分析方法

謝開仲梁棟謝松茂魏勇

1.廣西大學土木建筑工程學院，南寧 530004；2.廣西大學防災減災與工程安全重點實驗室，南寧530004

靜力非線性（Nonlinear Static Procedure）分析方法即Pushover方法，是基于性能設計新結構或者評估現有結構的一種方法，在結構抗震性能研究中廣泛應用。Pushover方法最初發展于建筑結構［1-3］，尤其是高層建筑，該方法給出了強震作用下結構的目標位移，一般為頂層位移，可以快速評估高層建筑的抗震性能，不必進行復雜的非線性時程分析。由于Pushover方法只對單一方向進行抗震分析，學者們對水平多向耦合地震進行了研究［4-5］。與非線性時程分析方法相比，Pushover方法原理簡單、實施方便，因此逐漸應用到橋梁結構中［6-7］。橋梁結構的側向性能比較復雜，Pushover方法主要應用于橋墩性能的研究［8-9］。一般假設地震反應由橋梁結構的一階振型控制，但高階振型的影響不可忽視［10-12］。考慮高階振型的影響時，結果精度得到一定的提高。對于拱結構，Pushover方法的評價指標不再是橋墩，而是主要的承力結構-拱肋，其空間性能尤為復雜。對于拱結構的Pushover方法已有學者進行了研究［13-14］，主要集中在石拱橋和單拱結構以及鋼管混凝土拱橋，勁性骨架拱橋則少有研究。文獻［15-16］采用非線性時程分析方法分析了行波效應對勁性骨架拱橋的抗震性能，而Pushover方法的適用性有待研究。

本文基于Pushover方法的基本原理，根據勁性骨架拱橋的受力形式以及動力性能，對一座鐵路上承式鋼筋混凝土勁性骨架拱橋進行靜力非線性分析，采用不同的加載方式構建結構的能力譜曲線，并根據地震波記錄建立需求譜曲線，求解結構的性能點，并與非線性時程分析結果進行對比，評估不同震級下結構的損傷狀態。

1 基于Pushover的拱橋抗震評估方法

1.1 基本假設

Pushover方法假定：①結構的反應由第一振型控制；②結構沿高度的變形可由形狀向量｛φ｝表示，且在整個地震反應過程中變形形狀保持不變。

1.2 基于目標位移的能力譜法

能力譜法主要基于多自由度體系的動力方程，將其轉化為單自由度體系的動力方程進行求解。核心是通過將Pushover方法獲得的結構基底剪力合力-特征點位移關系曲線轉換成結構的能力譜曲線，在同一坐標系下繪出能力譜曲線與地震動需求譜曲線，以圖解或數值解析的方式來求解交點，檢驗結構的抗震性能。Pushover方法主要是獲取結構的能力譜曲線，分析時需要確定一個控制節點來描述結構的位移響應，可以選擇結構最大位移反應的節點位置。對于拱橋控制節點可選擇拱頂質心節點。

水平荷載分布模式應使所求的位移大致反映結構在地震作用下真實的位移響應，從而最大程度地反映結構的地震破壞機理。工程中應用較多的有荷載均勻分布、倒三角分布、拋物線分布、一階振型分布、等效基本振型分布、振型組合分布等分布模式。本文采用均勻分布、倒三角分布、一階振型分布的加載模式，計算式分別為

將Pushover方法得到的曲線轉換成能力譜曲線，并按照等能量原理進行雙線性化，見圖1。其中，Ay為等效屈服譜加速度；Dy為等效屈服譜位移；Du為極限譜位移。

圖1 能力譜的等效雙線性化

對于多自由度體系可按下式轉換，即

式中：A和D分別為譜加速度和譜位移為第i振型參與質量；un為荷載作用下所選控制點的位移為第i振型的參與系數；φni為第i振型控制點的位移。

1.3 結構性能點的確定

對于結構性能點可以采用強度折減法進行求解，即通過建立Ry-μ-T關系，將彈性反應譜折減為彈塑性反應譜，對結構的非線性地震響應進行求解。其中，Ry為強度折減系數，μ為結構的延性比；T為結構的自振周期。Ry可按下式計算。

式中：Fi為結構i節點的側向荷載；n為節點總數；wi為第i節點結構的重量；Vb為基底剪力合力；hi為基底與第i節點位置間的距離；ψ1i為主振型在第i節點處的振幅。

根據結構的周期以及延性比，計算得到地震動下結構的非線性反應譜，即地震動需求譜。譜位移D和譜加速度A計算式分別為

式中：Ae為彈性設計反應譜在（T，ξ）處的擬加速度，ξ為體系的阻尼比。

具體求解時可以假設μ=1，求得D和A，然后增大μ，不斷迭代求得一系列點。連接各點使其與能力譜相交，交點即為性能點，見圖2。圖中0.5、1、2、5、10 s為地震動需求譜的周期線。

圖2 性能點求解圖示

1.4 結構抗震性能評估

通過損傷指數（Damage Metrics，DM）來評價結構或者構件在地震作用下的損傷情況。采用位移作為損傷模型指標建立的損傷模型主要有四種：延性地震損傷模型、剛度退化地震損傷模型、累計滯回耗能地震損傷模型和雙參數地震損傷模型。本文采用剛度退化地震損傷模型進行抗震性能評估，如圖3所示。

圖3 剛度退化地震損傷模型

該模型損傷指數ηDM按下式計算：

式中：Kr為性能點處的割線剛度，反應損傷積累后的退化剛度，Kr=Ap/Dp，Ap·為結構性能點對應的擬加速度，Dp為結構性能點對應的擬位移；K0為能力譜曲線的初始剛度，即彈性階段的剛度，K0=Ay/Dy，Ay和Dy均由雙線性化的能力譜曲線確定。

結構在遭受不同強度地震時發生的破壞情況有所差異，有必要確定具體的標準來判斷結構的損傷情況，從而評估其損傷程度。根據鋼筋混凝土框架結構震害等級與損傷指數的關系，確定勁性骨架拱橋損傷指數，見表1。

表1 勁性骨架拱橋震害等級與損傷指數的關系

2 工程實例

2.1 橋梁概況

一座客運高速鐵路大橋設計方案為上承式鋼管混凝土勁性骨架拱橋，主拱形式為提籃拱，計算跨徑600 m，矢高150 m，拱腳寬40 m，拱頂寬16 m。主拱圈采用分離式雙箱拱，拱腳處單個箱拱寬9 m，拱頂處單個箱拱寬6 m，兩拱箱間設橫向連接。弦桿鋼管采用Q460鋼，直徑1 m，鋼管厚32 mm，管內灌注C80自密實混凝土，外包混凝土采用C70混凝土。拱上共有9個立柱和2個過渡墩。上部結構為8×56 m的Ⅰ型鋼結合梁+2×89 m T構。橋梁結構的三視圖見圖4。

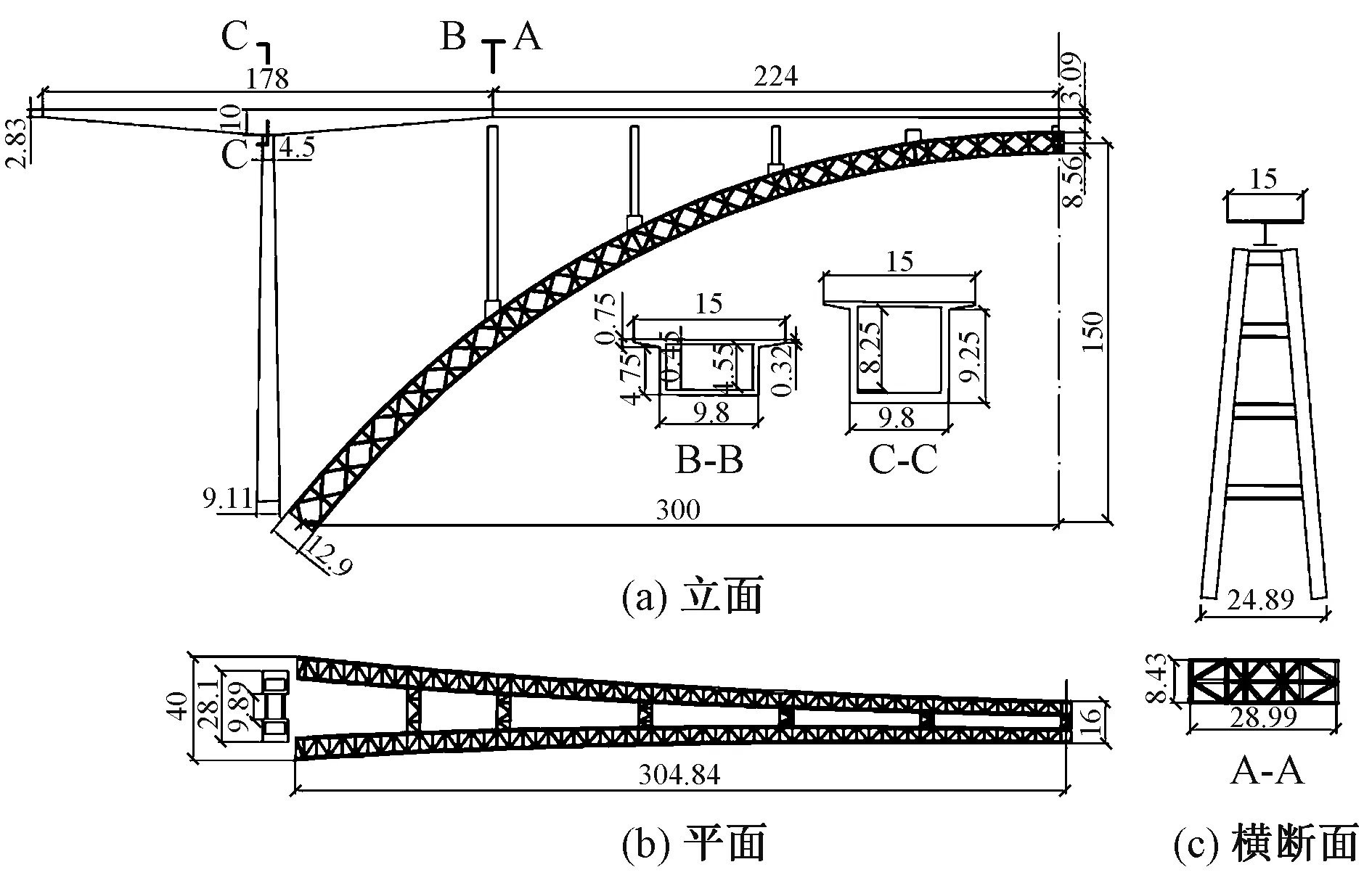
圖4 橋梁三視圖（單位：m）

2.2 有限元模型

基于有限元軟件ANSYS建立空間有限元模型，拱肋弦桿、腹桿、橫聯、橫向聯系、立柱、蓋梁、主梁均采用考慮剪切變形的梁單元beam188模擬，其中弦桿采用復合材料截面模擬。外包混凝土采用shell181單元模擬，板單元與梁單元共節點，基座采用solid186單元模擬，二期恒載通過mass21單元添加。縱橋向為x軸，橫橋向為y軸，豎橋向為z軸。全橋共節點1 835個，梁單元4 824個，板單元1 400個，實體單元26個、質點單元160個。拱腳與交界墩底部約束全部自由度，立柱基座底部與拱圈共節點，立柱與立柱基座耦合全部自由度，蓋梁與立柱共節點，主梁與蓋梁間耦合豎向和橫向自由度。通過模態分析研究動力特性，采用子空間法提取振型。結構前六階振型及對應頻率見圖5。

圖5 結構前6階振型及對應頻率

由圖5可知，橋梁的前六階頻率均較小且較接近，結構自振頻率為0.271 Hz，自振周期較大。一階振型屬于主梁和主拱對稱側彎，表明結構的側向剛度較小。由于大跨度拱橋寬跨比較小，極易發生側傾失穩，特別是在地震發生時其橫向振動是主導橋梁破壞的主要形式。二階振型屬于主梁與主拱反對稱豎彎，表明豎向剛度比橫向剛度大。前六階振型有四階振型表現為橫向側傾或橫向彎扭組合，因此應更加關注大跨度拱橋橫向穩定性。

2.3 基于Pushover的抗震分析

2.3.1 材料的本構關系

1）在分析勁性骨架混凝土拱橋的穩定性時，考慮鋼管對核心混凝土的套箍作用。核心混凝土的本構關系可參考文獻［17］的研究結果。

2）鋼管視為理想彈塑性材料，采用雙線性等向強化模型模擬。

3）普通混凝土采用多線性等向強化模型模擬。混凝土應力σc的計算式為當εc≤ε0時

式中：εc為混凝土應力；fc為混凝土強度設計值；ε0為混凝土峰值應變，取0.002；εcu為混凝土極限壓應變，取0.003 3；n為系數，取2。

2.3.2 能力譜分析

由于橋梁結構的第一階振型為橫向振動，故只考慮橫向一階振型，計算橋梁的抗震性能。根據振型選擇不同的加載方式，取位移最大的拱頂質心節點為位移控制節點，得到基底剪力-位移曲線以及能力譜曲線，見圖6。

圖6 基底剪力-位移曲線以及能力譜曲線

由圖6（a）可知：①隨著荷載的增加拱頂位移逐漸增大，結構逐漸從線性階段到達彈塑性階段。拱頂位移達到1.80 m時，橋梁結構逐漸從線性階段進入屈服階段，荷載-位移曲線表現為非線性。在拱頂位移達到6.0 m時基底剪力達到極值，而拱頂位移迅速增大，表現出大變形的特征，橋梁結構失去原有的穩定，逐漸破壞倒塌。②三種加載方式的基底剪力極值相差較大，一階振型加載、倒三角加載、均布加載時基底剪力極值分別為4.0×105、6.2×105、7.9×105kN。③為模擬地震作用下真實的位移響應，采用振型和地震動慣性力作為不同的假設條件，得到的基底剪力及能力譜不同。因此對于大跨度拱橋應同時考慮結構的地震動慣性力和振型，不能直接以基底剪力作為地震評估的依據。

由圖6（b）可知，三種加載方式得到的譜加速度不同，均布加載、倒三角加載、一階振型加載的譜加速度逐漸減小。然而地震作用下的結構響應未知，僅依據能力譜曲線無法判斷三種加載方式對大跨度拱橋抗震性能評估的優劣。

2.3.3 結構性能點的求解

地震波記錄選取E1波次方向并調整至0.8g，其地震波記錄以及擬合反應譜見圖7。

圖7 E1地震波記錄及反應譜

根據式（6）、式（7）將圖7（b）中的擬合反應譜進行轉化得到圖8。圖中保留了部分地震需求譜，虛線表示迭代過程，a-b連線與雙線性能力譜的交點即為結構性能點。可知，三種加載方式作用下結構性能點的譜位移（圖8中性能點的橫坐標）比較接近。

圖8 結構性能點的求解

結構性能點計算結果見表2，其中基底剪力和拱頂位移，通過得到的性能點按式（4）進行計算。可知，三種加載方式下結構達到目標拱頂位移施加的基底剪力相差較大，均布加載為一階振型加載時的兩倍。一階振型加載結構的基底剪力最小，為三種加載方式中最不利荷載分布形式。不同加載方式下結構的拱頂位移比較接近，誤差在10.8%以內，地震作用下結構的峰值位移在3.2 m左右。

表2 結構性能點計算結果

為了驗證能力譜結果的準確性，采用相同地震波對結構進行非線性時程分析，取反應最劇烈的前15 s，結構阻尼采用Rayleigh阻尼，采用質量參與系數較大的第一、四階振型計算比例系數。計算結果對比見圖9。可知，兩種方法中結構的拱肋線形基本一致。①從拱腳至L/8截面，倒三角加載方式與時程分析的橫向位移幾乎重疊，一階振型加載和均布加載與時程分析有所偏差，但仍在合理范圍內。②從L/8截面至拱頂則是一階振型加載與時程分析比較接近，均布加載和倒三角加載比時程分析的結果大10%左右。③對于拱肋的應力，在拱腳位置三種加載方式均與時程分析一致，拱肋其他位置如L/2、L/8截面，一階振型與時程分析結果更接近，而均布加載和倒三角加載模式有較大的誤差。④結構的應力突變位置和屈服位置可以用三種加載方式來評估。比如三種加載方式和時程分析結果顯示在0、L/8、7L/8和L截面達到屈服。一階振型加載方式與結構地震的反應更接近，評估結果更準確，驗證了Pushover方法應用于大跨度勁性骨架拱橋抗震性能評估中的可行性。

圖9 能力譜分析與時程分析結果對比

2.3.4 結構抗震性能評估

采用剛度退化地震損傷模型計算結構的損傷指數，對橋梁結果的地震損傷進行評估。性能點求解采用一階振型加載方式，損傷評估結果見表3。

表3 不同地震強度損傷評估結果

由表3可知：結構的抗震能力較強，0.3g、0.4g地震作用下橋梁結構均基本完好；0.8g地震作用下橋梁發生了輕微破壞；1.6g、2.0g地震作用下發生中等破壞，主要承重結構進入彈塑性階段，結構處于危險狀態；4.0g時橋梁遭受嚴重破壞，危害較大。

3 結論

1）大跨度拱橋Pushover分析中，一階振型加載方式的性能點求解更準確，倒三角加載次之，均布加載方式誤差最大，但三種加載方式的偏差在10%以內。

2）Pushover分析與非線性時程分析的應力突變位置和屈服位置比較接近，驗證了Pushover方法應用于大跨度勁性骨架拱橋抗震性能評估的可行性。

3）在8度、9度地震作用下結構基本完好，0.8g地震作用下結構發生輕微破壞，1.6g、2.0g地震作用下發生中等破壞，4.0g時遭受嚴重破壞。

本文研究結果表明，拱橋在地震作用下高階振型的影響顯著，縱向、豎向地震作用不可忽視，Pushover方法的應用有待進一步研究。