直驅風機機網側變流器統一建模及其弱電網下穩定性研究
汪春江,孫建軍,宮金武,查曉明
(武漢大學 電氣及自動化學院,武漢 430072)
0 引 言
可再生能源發電并網是緩解能源危機,降耗去霾的有效途徑[1],風電作為可再生能源發電的一種主要形式,近年來在國內得到快速發展,電網中風電占比不斷攀升。然而,風速固有的隨機性、波動性、間歇性等特性,勢必對電力系統的安全穩定運行帶來不可忽略的影響,尤其是并入弱電網時影響尤為惡劣。國內外已出現多起這類穩定性問題,振蕩頻率跨越10 Hz-1 000 Hz[2-5]。這種由風電變流器控制引起的振蕩頻率和衰減率由控制參數和交流電網參數決定,且比次同步諧振發散得更快,應引起足夠的重視[6-7]。因而,研究弱電網下風電的穩定性問題勢在必行[8]。
針對弱電網下風電并網的穩定性問題,目前國內外在這方面已經有一部分研究進展。由于風電變流器普遍采用的背靠背拓撲形式,使得機側和網側變流器動態在一定程度上解耦,在研究變流器控制的穩定性時常常將機側和網側變流器其一進行簡化。文獻[9]研究了影響雙饋風機軸系振蕩的因素,考慮軸系、發電機及機側變流器控制動態,認為機側控制參數和控制策略的不當會引發不穩定現象;文獻[10]則研究了直驅風機發生次同步振蕩的機理,將風力機、永磁同步發電機和機側變流器及其控制系統簡化建模為受控電流源模型,認為風機臺數的增多和電網強度的變弱引發系統阻尼變弱導致不穩定;以上研究都忽略了網側控制的動態,將其等效為恒壓源。文獻[11-12]研究弱電網下直驅風機的穩定性問題,認為網側變流器的控制參數與控制策略對穩定性有關鍵性影響,而鎖相環控制涉及到與電網電壓的同步,也對穩定性至關重要。以上研究都忽略了機側控制的動態,將其等效為恒功率源。
以上研究并沒有同時考慮機側及網側控制,從系統多時間尺度控制的角度,機側與網側控制的時間尺度是存在重疊的[13],即同一時間尺度內,同時存在機側和網側變流器控制的影響。因此,需要同時考慮機側及網側變流器控制動態的影響。
傳統的變流器并網穩定性分析方法主要有狀態方程法[11]和阻抗法[14]。阻抗法目前多用于網側變流器并網穩定性分析中,在這類分析中,機側變流器動態被忽略,因此無法利用阻抗法分析考慮機網側變流器控制的并網穩定性。
綜上,文章針對弱電網下直驅風機的穩定性問題,首先建立含直驅風機機網側變流器控制的統一模型;在此基礎上,提出了包含機網側變流器控制的穩定性分析方法,對比傳統的阻抗分析方法,并進行了相應的實例分析;最后通過simulink仿真對分析的結論進行了驗證。
1 直驅風機變流器控制
1.1 機側變流器控制
文章研究的直驅風機機網側變流器控制框圖如圖1所示。
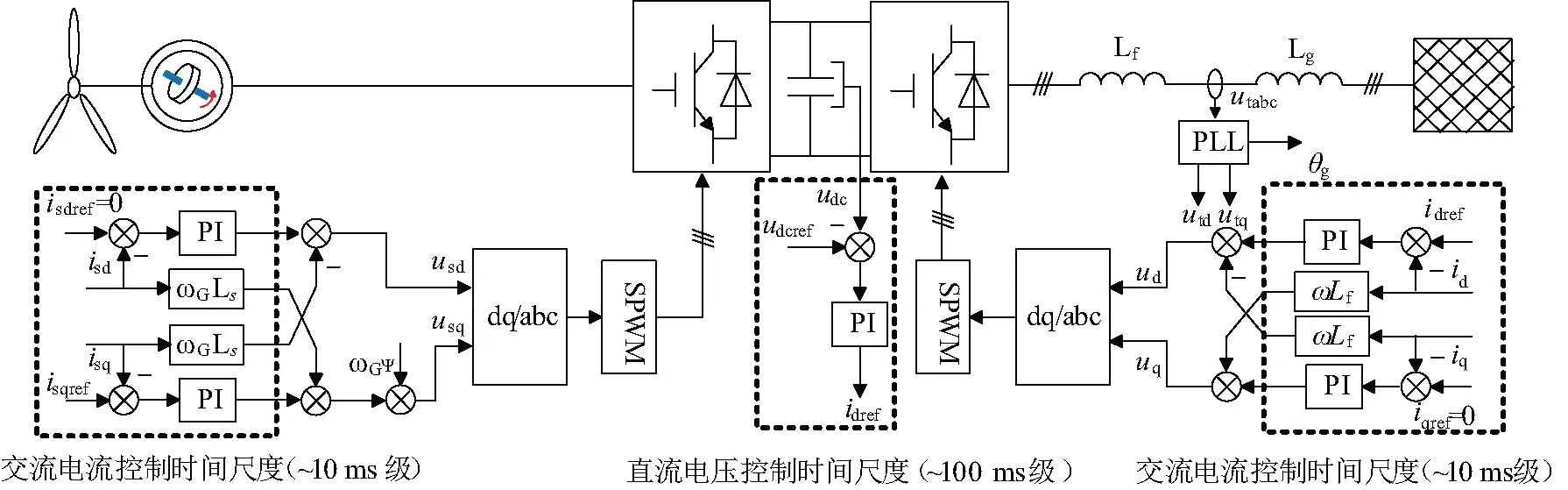
圖1 直驅風機機網側變流器控制框圖
如圖1所示,機網側控制分兩個時間尺度,直流電壓控制時間尺度與交流電流控制時間尺度,在交流電流控制時間尺度內,機網側實際存在耦合的。因此,考慮含交流電流時間尺度動態時,機網側動態應同時考慮。
機側采取轉子磁場定向的矢量控制,d軸定位于轉子永磁體的磁鏈方向上。該永磁同步發電機的電壓方程及轉矩方程為:
(1)
式中Rs、Ls分別為發電機的定子電阻、電感;us、is分別為定子電壓電流;下標d、q代表d軸、q軸分量;ωG為發電機轉速;Ψ為轉子永磁體磁鏈;p為電機極對數。發電機轉矩直接由定子電流q軸分量控制。
控制器外環控制轉速,內環控制定子d、q軸電流,均采用PI控制,控制關系如下:
(2)
式中kp、ki分別為PI控制的比例及積分系數;下標ref為該項變量的指令值。
1.2 網側變流器控制
如圖1所示,網側變流器控制采取電網電壓定向的矢量控制。其電壓方程為:
(3)
式中Lf為濾波電感;u、i分別為變流器輸出電壓電流;ut為濾波后電壓;ω為電網側電壓角速度;下標0代表穩態值。
控制器外環控制直流側電壓,內環控制電網d、q軸電流,均采用PI控制,控制關系如下:
(4)
1.3 弱電網特性
考慮弱電網情形,即電網存在較大的阻抗(用電網電感模擬),其電壓方程為:
(5)
式中Lg為電網電感;ug為電網電壓。
2 小信號模型
2.1 機側變流器控制建模
對式(1)、式(2)進行小信號化處理,認為轉速不變,有:
(6)
(7)
聯解上述公式:
(8)
在變流器并網的穩定性分析中,常常將機側變流器等效為一個恒功率源,即ΔPG=0,這樣實際上是忽略了機側變流器的控制動態對穩定性的影響,而考慮到如上的機側變流器控制動態,機側變流器的輸出功率為:
ΔPG=ωG0ΔTG=T1(s)·Δisqref
(9)
其中:
2.2 網側變流器控制建模
對式(3)~式(5)進行小信號化處理,有:
(10)
(11)
(12)
對于網側變流器,其交流側輸出功率如下:
(13)
小信號化:
(14)
聯解上述公式,有:
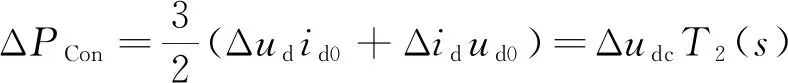
(15)
其中:
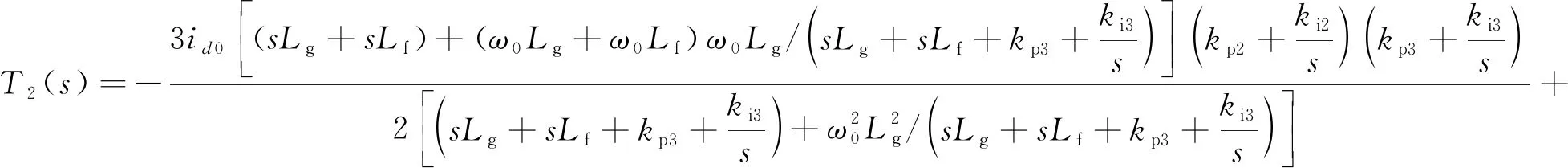
(16)
3 穩定性分析
3.1 阻抗分析方法
使用阻抗分析法,則忽略機側變流器控制動態,機側變流器輸出功率認為是恒功率,即ΔPG=0。并網系統可以化為如圖2所示等效電路。
Zi、Zo分別為電網阻抗矩陣,變流器輸出阻抗矩陣,Δis、Δug、ΔuPCC、Δi分別為變流器受擾動后空載電流變化量、交流電網受擾動后空載電壓變化量、并網點電壓受擾動后變化量、并網電流受擾動后變化量。由疊加原理,該系統滿足關系式:
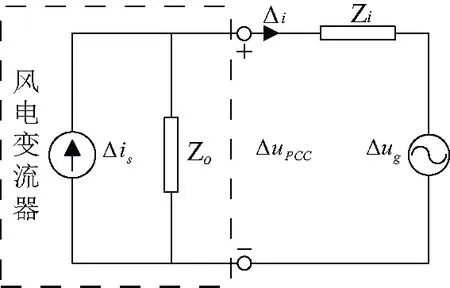
圖2 并網系統等效電路
ΔuPCC=[E+YoZi]-1(Δug-ZiΔis)
(17)
文中所有加粗量均為矩陣或向量,E為單位矩陣,Yo為矩陣Zo的逆。對于圖2所示的三相逆變器并網系統,(E+YoZi)-1是一個2維矩陣,記為矩陣G:
(18)
式(17)可以寫作:
(19)
式中y為輸出;u為輸入:
y=ΔuPCC,u=Δug-ZiΔis
(20)
在實際系統中,由于逆變器和電網在獨立運行時一般是穩定的,即u是穩定的,因此并網系統的穩定性由G的零極點分布決定。對于2輸入2輸出系統,閉環系統穩定等效為Gdd、Gdq、Gqd、Gqq均沒有右半平面的極點,文中以分析Gdd為例。變流器輸出阻抗如下,依據為式(10)~式(11):
(21)
交流電網的輸入阻抗如下,依據為式(12):
(22)
3.2 統一建模穩定性分析方法
系統的動態特性反應到電氣量上是交直流電壓電流的變化,而不穩定是輸入輸出功率不平衡的表現。分析系統的交直流側瞬時功率關系如下。
有小信號關系式:
(23)
結合之前建立的小信號模型,可以得到如圖3、圖4所示的穩定性模型。
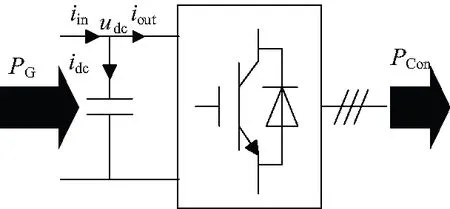
圖3 交直流側瞬時功率平衡關系
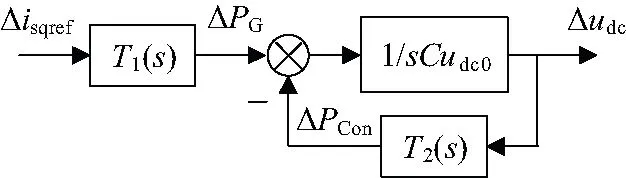
圖4 穩定性分析模型
如上述模型所示,系統的穩定性用直流電壓的穩定性來表征。Δisqref是風機定子電流指令值擾動量,該值由風機最大功率跟蹤控制決定。即直驅風機并網系統的穩定性受控制參數、電網電感及最大功率跟蹤控制動態影響。
3.3 實例分析
分析及仿真采用的直驅風機并網系統參數如表1所示。
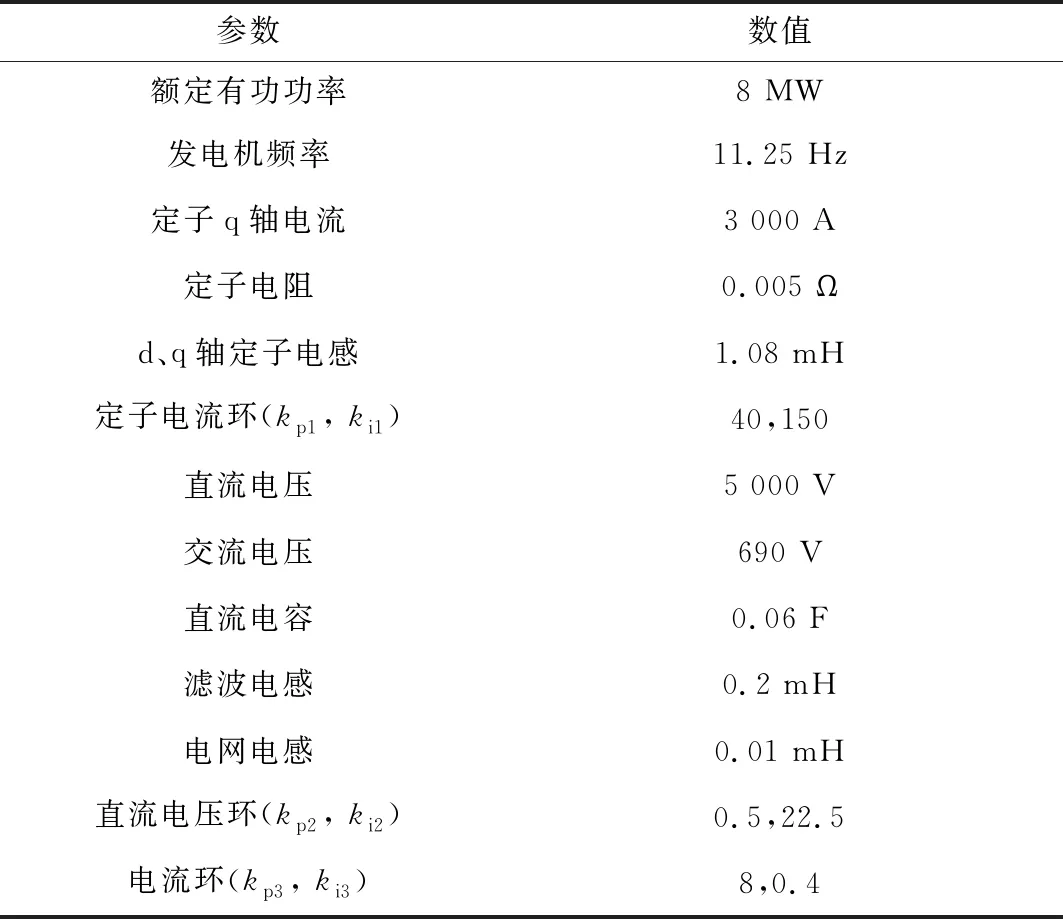
表1 直驅風機并網系統參數
根據上文所述的阻抗分析法及統一建模穩定性分析方法,得到閉環系統的極點分布如圖5所示。 此時,系統穩定性分析存在兩種結果,統一建模分析法的結果是系統仍舊穩定,而傳統的阻抗分析法得到結果系統已經失穩,二者存在差異性。很明顯,對于阻抗分析法而言,0.01 mH已經是分析得出的系統失穩時的電網電感邊界。增大電網電感,利用統一建模分析繼續計算極點。

圖5 閉環極點分布對比圖
對于文中采用的統一建模分析法而言,0.03 mH才是系統失穩時的電網電感邊界。明顯,阻抗分析法在分析電網電感邊界時擁有更強的保守性,如圖6所示。
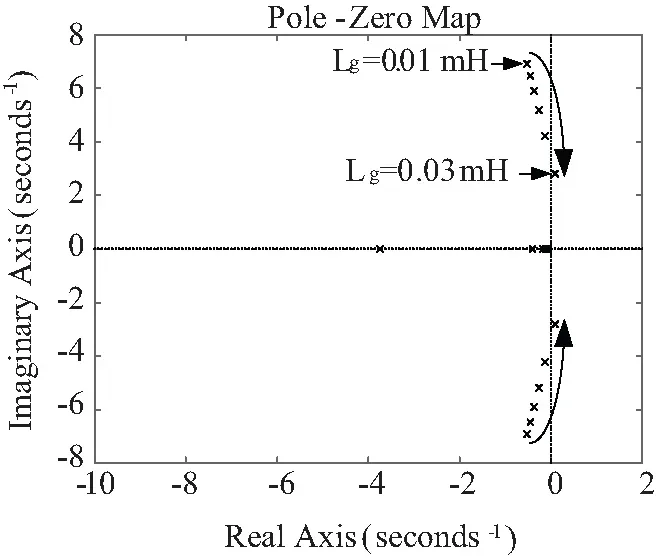
圖6 電網電感增大時閉環極點分布
4 仿真驗證
依據表1的參數及圖1的拓撲及控制框圖,搭建Simulink仿真模型以驗證上述分析。如圖7所示為仿真得到的直流電壓波形。
直驅風機在初始的并網動作之后,直流電壓迅速回復到5 000 V的額定值,此時系統是穩定的,與統一建模分析法的結果相符。增大電網電感,探尋仿真情況下電網電感失穩邊界,如圖8所示。
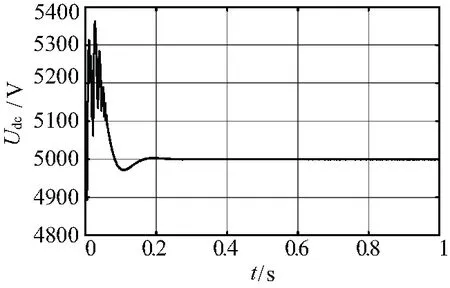
圖7 仿真直流電壓波形
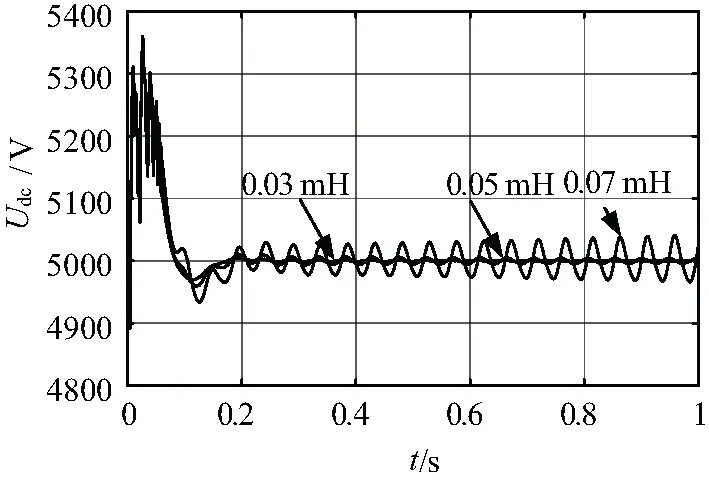
圖8 電網電感增大時直流電壓波形
陸續增大電網電感至0.07 mH,在初始的并網動作之后,直流電壓沒有回復至5 000 V,而是在5 000 V附近出現了20 Hz頻率的增幅振蕩,此時,系統開始失穩。比較阻抗分析法的0.01 mH與考慮機網側變流器控制的統一建模分析法的0.03 mH,文中提出的分析方法具有更弱的保守性,對于預測直驅風機并入弱電網的電網電感邊界有更高的精確性。
5 結束語
文中研究了弱電網下直驅風機并網的穩定性問題,建立了考慮機側和網側變流器控制耦合的統一分析模型,并給出了考慮機側和網側變流器控制的穩定性分析方法,并利用Simulink仿真對分析結果進行了驗證,得到以下結論:
(1)直驅風機機網側變流器控制之間存在時間尺度上的耦合,在分析并網穩定性時只考慮網側將造成分析誤差;
(2)直驅風機并網系統的穩定性不僅受機網側控制參數及電網電感決定,還受最大功率跟蹤控制動態影響;
(3)考慮機網側變流器控制的統一建模分析方法,比較傳統的阻抗分析法,具有更弱的保守性,對于預測直驅風機并入弱電網的電網電感邊界有更高的精確性。

