低空反無雷達的高精度測速方法及波形設計

楊雪亞 沈顯照 王賢翔

(1.中國電子科技集團公司第三十八研究所 合肥 230088；2.孔徑陣列與空間探測安徽重點實驗室 合肥 230088)

0 引言

近年來，小型無人機在各行各業得到了廣泛的應用，同時也給低空安全帶來了巨大的挑戰。小型無人機通常在低空或超低空飛行，飛行速度慢，且機身體積小，利用傳統的檢測手段很難將其從復雜的雜波背景中檢測出來，這成為反無人機系統的技術難點。目前反無系統采用的探測手段包括聲學探測、無線電掃描、光學探測及雷達探測，其中雷達探測憑借其全天候、全天時、探測距離遠、測量精度高等特點，成為反無系統的首選。

國內外在低空反無雷達方面了做了大量的研究，文獻[4]研究了低空小型無人機雷達的探測距離，給出了無人機RCS的計算模型和雷達方程。文獻[5]給出了基于深度學習的特征提取的無人機檢測識別方法。文獻[6]研究了基于無人機旋翼微多普勒效應的目標檢測和跟蹤方法。文獻[7]研究了長時間積累提高小型無人機檢測信噪比的思路，并進行速度估計和運動補償消除運動目標的距離徙動和多普勒擴散。文獻[8]利用線性調頻信號的距離多普勒耦合現象實現單脈沖測速。文獻[9]提出了一種對目標回波主瓣面積梯形近似并插值估算多普勒頻率最大值位置的方法。

本文針對雜波背景下低空反無雷達對小型無人機的探測問題，研究提高測速精度、改善雜波背景下無人機探測能力的方法。首先給出了采用基于多普勒頻道幅度服從高斯分布的高精度測速方法，顯著提高了無人機的速度測量精度。然后采用一種通過短、長脈沖交替發射增大短脈沖積累時間的波形設計方式提升速度分辨力。最后通過仿真和實測數據處理結果驗證了本文方法的正確性。

1 信號模型

低空反無雷達通過發射線性調頻脈沖及脈沖串MTD濾波的方式獲取脈沖壓縮增益和相參處理增益。線性調頻信號形式為

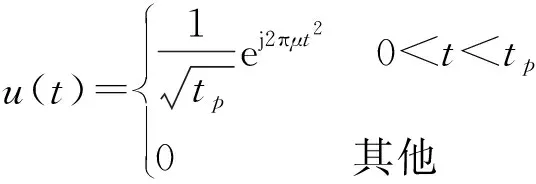
(1)

第個脈沖回波信號經脈沖壓縮后可表示為

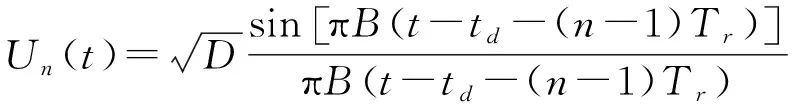
(2)

其中，為線性調頻信號的時寬帶寬積；為信號帶寬；為回波延遲時間；為脈沖重復周期。

對脈沖壓縮信號做階MTD濾波處理，則第個濾波器的幅度響應為

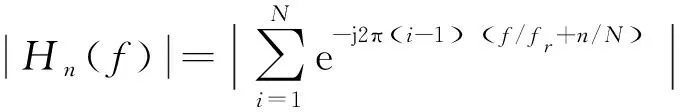
(3)

濾波器的峰值位于=±,1±,2±處。相鄰濾波器的頻率間隔為

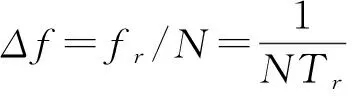
(4)

式(4)表示多普勒分辨力，為積累時間的倒數。則速度測量誤差為式(5)所示。

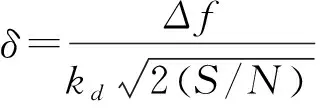
(5)

其中為測速環路誤差斜率，一般可取12～14之間。

2 高精度測速方法

設目標的多普勒頻率為，回波信號經過波束形成、脈沖壓縮及MTD濾波之后，在第個MTD濾波器的幅度最大為，在前、后相鄰濾波器的幅度分別為-1和+1，三組濾波器的中心頻率分別為-1,,+1，如圖1所示。

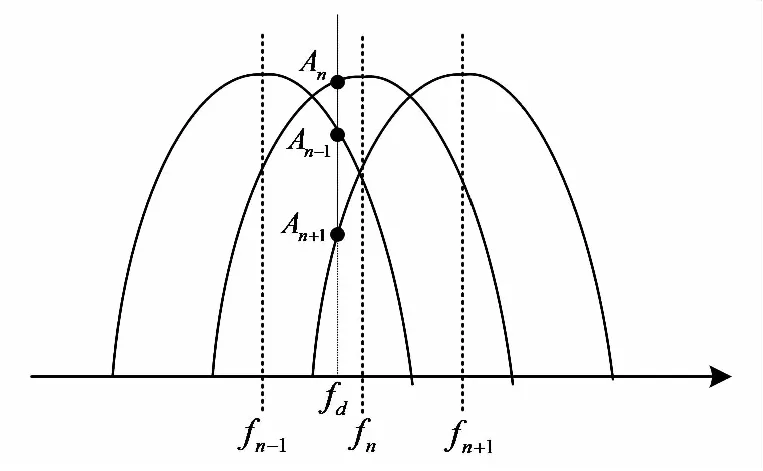
圖1 高精度測速方法示意圖

MTD濾波器的響應可認為服從高斯分布，且每組濾波器的響應曲線一致，則三組濾波器的幅度響應可表示為

=e-(-),=-1,,+1

(6)

其中為濾波器中心的幅度，為比例常數。

對和-1取對數并相減，可得

=--1=[(--1)-(-)]

(7)

同理，對和+1取對數并相減，可得

=-+1=[(-+1)-(-)]

(8)

由式(7)和式(8)可得

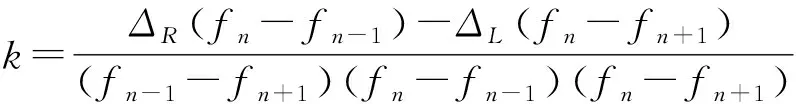
(9)

將式(9)代入式(7)，經過運算可得

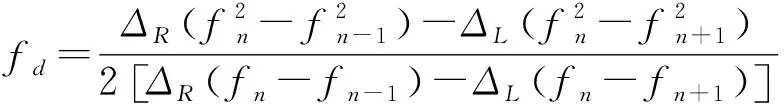
(10)

對于中心頻率等間隔的MTD濾波器，--1=+1-，則式(10)可簡化為

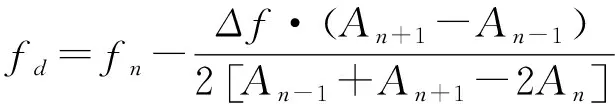
(11)

相比基于均勻分布的質心法，式(11)的計算方法更接近MTD濾波器的真實幅度響應曲線，因此能改善多普勒速度的測量精度。

3 長時間積累波形設計

低空反無雷達需要探測近區小型無人機和遠區空中目標，因此采用近距離補盲和遠距離正常兩種波形。對于近距離補盲波形，其作用距離通常在10 km以內，而遠距離正常波形的作用距離可達100 km。傳統的波形設計方式是先后發射補盲和正常兩組CPI，對兩組CPI分別進行相參處理，補盲脈沖和正常脈沖的重復周期分別是1和2，脈沖數均為，如圖2所示。

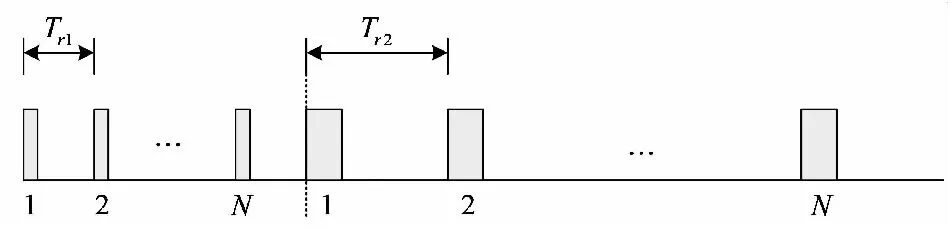
圖2 傳統的兩組CPI發射波形

設1為0.1 ms、2為1 ms，積累脈沖數為64。補盲CPI的多普勒分辨力Δ=156.25 Hz，正常CPI的多普勒分辨力Δ=15.625 Hz。對于補盲CPI而言，其速度分辨力較低，顯然無法利用速度信息將慢速運動目標從近區強雜波背景中分辨出來。

由式(4)和式(5)可見，通過增加積累時間，可提高速度分辨力和速度測量精度。因此，在總駐留時間不變的前提下，將上述發射波形進行優化，把每個補盲脈沖和正常脈沖合成為一個大脈沖，順序發射個大脈沖，在后端處理時，將每個大脈沖內的補盲脈沖和正常脈沖分離出來，形成補盲、正常兩組獨立的CPI分別處理，如圖3所示。

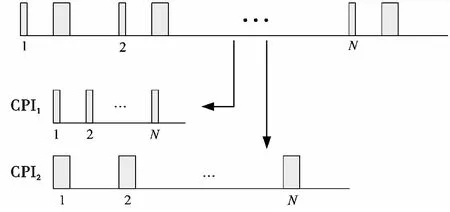
圖3 改進的波形設計形式

對于近區補盲和遠區正常波形，其積累時間均為70.4 ms，對應的多普勒分辨力14.2045 Hz，相比較傳統的波形設計，補盲波形的速度分辨力提升了10倍以上，顯著地改善了速度分辨力和測速精度。

4 仿真和實測數據處理

仿真徑向速度為20 m/s的目標回波信號，采用重復周期為0.1 ms、64個脈沖的發射波形，比較不同測速方法的精度隨積累信噪比的變化曲線，結果如圖4所示。對于MTD濾波后直接選大的測速方法，受濾波器中心頻率量化誤差的影響，其測速精度跟目標多普勒速度與濾波器中心頻率的相對位置有關(在0～0.5Δ間呈隨機分布)。對于質心方法，由于均勻分布模型與真實分布模型偏差較大，導致測速誤差大。而本文的高精度測速方法，根據三組濾波器的幅度和中心頻率計算目標的速度，不受目標多普勒速度與濾波器中心濾波的相對位置關系的影響，更接近真實的分布模型，獲得了更為準確的測速結果。

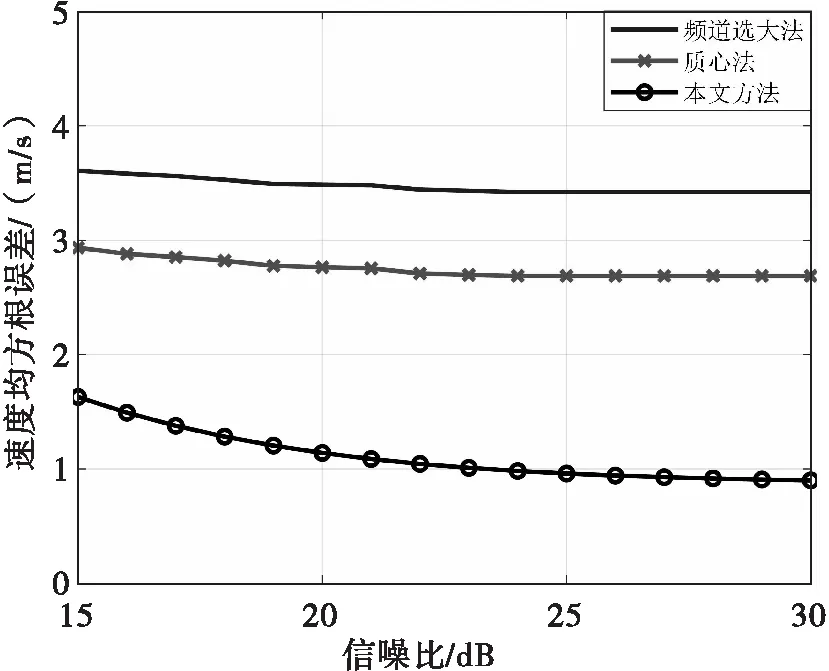
圖4 測速誤差隨信噪比變化曲線

基于以上仿真條件，比較傳統波形即補盲CPI、正常CPI先后發射，和補盲、正常脈沖交替發射的改進波形的測速精度，其中補盲脈沖和正常脈沖的重復周期分別為0.1 ms和1 ms。圖5給出了補盲波形的測速誤差對比結果，可見，改進波形的測速精度比傳統波形提升了一個數量級。這是因為改進的波形將遠距離正常脈沖的駐留時間包含在其積累時間內，顯著提高了補盲波形的速度分辨力和測速精度。

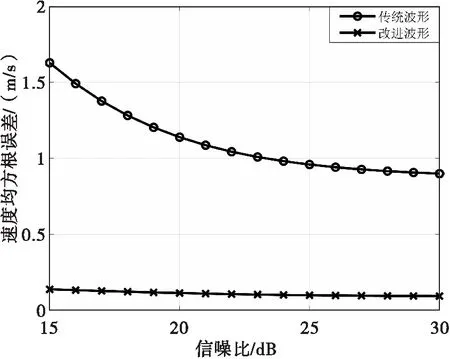
圖5 傳統波形和改進波形的測速精度對比

S波段低空反無雷達測試對大疆精靈四旋翼無人機的實際探測和測量性能，雷達使用補盲波形和正常波形交替發射的改進波形，在回波處理時將其分離成短、長兩組CPI分別處理。無人機從雷達處起飛，以高度200 m、速度13 m/s勻速飛行至5 km處折返。雷達在距離600 m左右發現目標并按照1 Hz的數據率對無人機進行跟蹤。圖6是無人機飛行過程中雷達點跡的測量速度和無人機GPS記錄的真實速度的比較，飛行前半段無人機背站飛行，后半段向站飛行，速度由-13 m/s變為13 m/s，雷達測量速度和無人機真實速度吻合較好。圖7是雷達測速誤差，可見最大速度誤差不超過0.3 m/s，飛行全程均方根誤差為0.075 m/s，實現了對小型無人機的高精度測速。

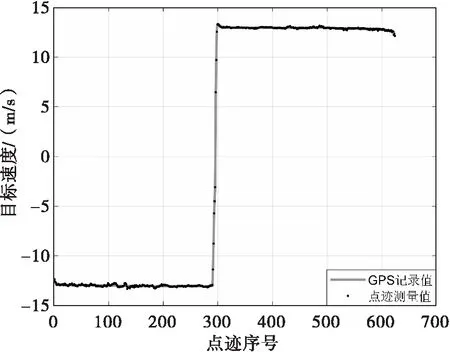
圖6 無人機飛行速度真實值和測量值

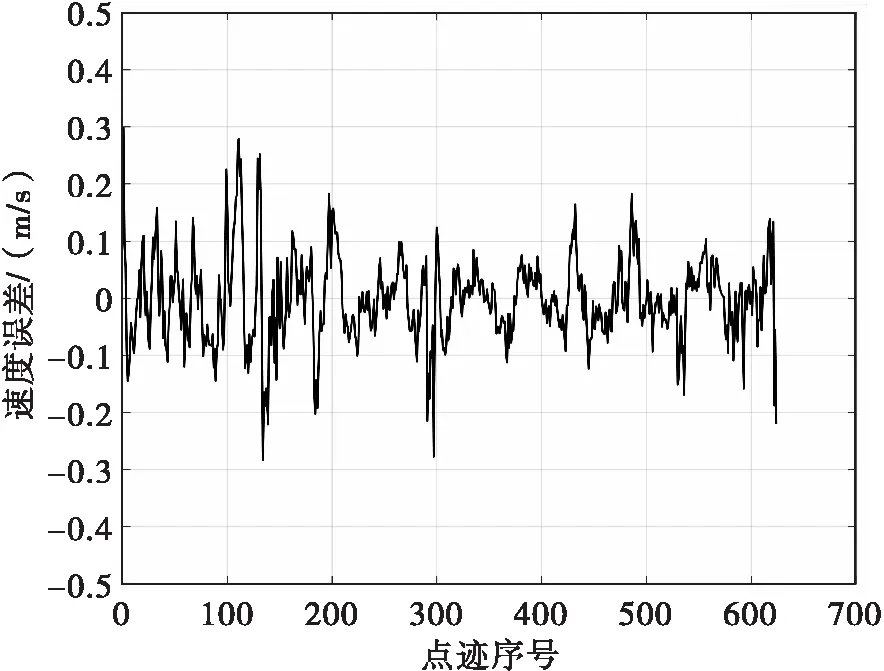
圖7 雷達對無人機的測速誤差

5 結束語

“低、慢、小”目標的探測，尤其是強雜波區中小型無人機的探測一直是低空反無雷達的技術難點。為了更多地利用目標的速度信息對慢速運動目標和雜波進行分辨，本文給出了一種基于濾波器幅度響應服從高斯分布的高精度測速方法，與頻道選大法和質心法相比，改善了速度測量精度。此外，采用一種改進的波形設計方式，充分利用整個駐留時間提升速度分辨力，在駐留時間不變的情況下，補盲脈沖的速度分辨力可提升一個數量級。仿真及實測數據分析結果表明了本文方法的有效性。