基于CFD和神經網絡的2級刷式密封結構泄漏和級間不平衡性分析

閻師，胡芳，黃首清，劉守文

（1.中國空間技術研究院，2.航天機電產品環境可靠性試驗技術北京市重點實驗室，3.北京衛星環境工程研究所：北京 100094）

0 引言

由于可以容忍刷絲束和轉子瞬時不同心并保持良好的密封特性，刷式密封結構在航空發動機中獲得了重要應用，是傳統迷宮密封結構的重要替代產品。隨著對壓比、推重比要求的不斷提高，航空發動機對刷式密封結構的承壓能力、泄漏特性有了更高要求，而多級刷式密封技術是高壓差密封的一種有效解決方案，可以同時獲得更優的密封特性并減小各級的壓降及刷絲束-和轉子的磨損。相對于上游，下游刷式密封結構承受了大部分的壓降。Hendricks等的試驗表明，對于一種2級刷式密封，上游刷絲束壓降為總壓降的40%，而下游為60%。這種分壓不均帶來級間不平衡性，下游刷式束承擔的較大的壓差也使刷絲束和轉子間的磨損較大，造成下游刷式密封性能過早失效，不利于多級刷式密封技術充分發揮其優勢。因此，研究影響刷式密封結構級間不平衡的影響因素和特性具有重要意義。

目前，有關多級刷式密封技術研究主要集中于流動特性和影響因素。Qiu等利用雷諾平均N-S方程耦合非達西多孔介質模型研究了多級刷式密封與迷宮密封混合密封技術的流動特性；Pugachev等將刷絲束視為多孔介質的3維CFD模型預測一種多級刷式密封結構的泄漏特性；黃首清等基于一種3維切片模型和刷絲接觸模型研究了2級刷式密封結構的泄漏、接觸力和轉矩特性；趙歡等研究了刷絲束徑向間隙、刷絲間隙、保護間隙對級間壓比的影響。需要指出的是，級間不平衡性的影響因素很多，而且具有較強的耦合性，現有研究主要為常規控制變量參數討論，時效性和適用性不足。正交分析等方法可以較大提高參數影響分析的效率，但只能獲得一些關鍵離散參數組合的結果。對于一些高度耦合和非線性的情況，也可采用基于2次多項式響應面方法，但是在實際應用時，響應面精度往往不足以有效逼近真實面。近年來隨著人工智能技術的興起，神經網絡等方法開始應用于復雜變量模型、強耦合效應模型的結果預測，利用經過良好訓練的神經網絡進行數據泛化預測具有很好的時效性和適用性。

本文基于CFD模型獲得泄漏量和級間壓比的訓練數據，設計神經網絡模型進行訓練，據此進行數據泛化預測，并討論了上下游刷絲排數和保護間隙對泄漏率、級間不平衡性的影響及刷絲排數和保護間隙之間的耦合作用。

1 CFD模型

1.1 切片式幾何模型

針對刷絲在周向循環對稱的結構特點，建立了刷式密封結構的一種3維切片式CFD模型，即周向寬度僅包含1根刷絲，軸向包含各排刷絲。2級刷式密封結構的3維切片式CFD模型如圖1所示。在模型中，上游入口和下游出口分別設置高壓和標準大氣壓，除了入口和出口之外的邊界均設置為靜態墻邊界。刷絲束區域的橫截模型如圖2所示。圖中平面1～4表明了2級刷封的上下游表面所在位置，各平面的壓力指面積權重平均壓力。上、下游級的壓差為

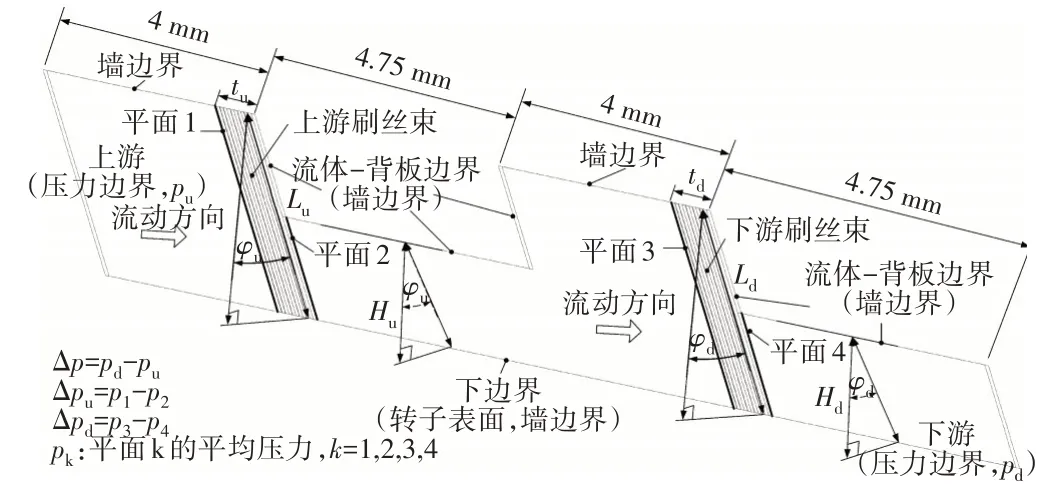
圖1 2級刷式密封結構的3維切片式CFD模型

圖2 刷絲束區域的橫截模型

在實際的刷式密封結構中，在壓差作用下刷絲束不可避免地發生壓縮和變形，使研究變得極端復雜。為便于研究，并結合刷絲實際排列規律，假設刷絲為均勻間隙蜂窩狀排列（圖2）。Lelli等的計算表明，是否考慮壓差作用下的刷絲束變形造成的流動差別小于10%，故忽略刷絲的移動和變形。

Dogu等利用多孔介質模型計算的結果表明，在刷絲根部附近壓力梯度很小。故圖1的模型中未對刷絲根部建模，大大減少網格數量和計算時間，且對CFD結果影響不大。

刷環的泄漏率用標況體積流率/（N·m/h）表示，與切片模型計算的質量流率/（kg/s）和周向循環數相關

1.2 模型參數

CFD模型主要參數見表1。

表1 CFD模型主要參數

1.3 網格及CFD求解設置

計算網格如圖3所示。刷絲間隙流體區域幾何形狀比較復雜，網格剖分非常細密，網格單元大小為0.0033 m。刷絲束的上游和下游網絡剖分適中，而由于刷絲不參與流體計算且不考慮移動和變形，故刷絲網格劃分最粗糙。

圖3 計算網格

刷絲束內部的流動是分析的重點。對于取表1參數的2級刷式密封模型，上游來流流速不大于1 m/s，按照保護間隙1.5 mm和30℃下空氣運動黏度為1.6×10m2/s，估算雷諾數為

在刷絲束內部，流速一般小于100 m/s，結合刷絲直徑為0.07 mm，計算對應的雷諾數為437.5。綜上，2級刷式密封模型的流動被視為層流型。

計算采用ANSYS-Fluent 14.0軟件，選擇可壓縮理想氣體流動、穩態3D求解器、2階迎風差分格式和SIMPLE算法。上述CFD模型和計算方法的準確性已通過試驗證明。

2 神經網絡模型

2.1 結構和算法

神經網絡包括輸入層、輸出層和隱層。考慮到泄漏率和級間壓比是反映2級刷式密封性能的重要指標，因此設置輸出層神經元為2個，分別代表泄漏率和級間壓比。而保護間隙和刷絲排數是影響泄漏率和級間壓比的重要參數，為了區別上下游參數的影響，設置輸入層神經元為4個，分別代表上游保護間隙、上游刷絲排數、下游保護間隙、下游刷絲排數。對于隱層的神經元數根據經驗公式

式中：為隱層神經元數；為輸入層神經元數。

因此隱層神經元數取9即可獲得足夠的精確性，考慮到MATLAB2019a神經網絡擬合工具箱推薦的默認值是10，因此確定層數為10。這樣，借助MATLAB的Neural Network Fitting工具箱建立的神經網絡結構如圖4所示。其中，神經元傳遞函數選擇雙曲正切的S型Tansig函數；訓練函數選擇Trainlm，即Levenberg-Marquardt算法；神經網絡預測性能用MSE和R評價，分別是目標值與預測值的均方誤差以及回歸相關系數。

圖4 用于預測泄漏率和級間壓比的神經網絡結構

2.2 數據訓練

訓練樣本根據CFD模型計算，給出了不同保護間隙和刷絲排數組合下的壓比和泄漏率結果，共20個樣本，見表2。其中，直接用于訓練神經網絡的樣本（訓練數據）占70%，即14個；而用于驗證（驗證數據）和測試（測試數據）的樣本分別占15%，即各3個。

訓練次數與均方誤差的關系如圖5所示。從圖中可見，訓練4次后，驗證數據和測試數據與預測值的均方誤差基本穩定，其中驗證數據與預測值的均方誤差達到0.0169（均方根誤差為0.13，在表2中泄漏率和級間壓比2列數據的平均值18.94的1%以下）；而訓練7次后，訓練數據與預測值的均方誤差小于10。而根據預測值與樣本值的相關系數（如圖6所示），二者滿足很好的線性關系，相關系數達到0.99997。綜上，可以認為本神經網絡得到了較好地訓練，可以用于泛化預測。

表2 訓練樣本

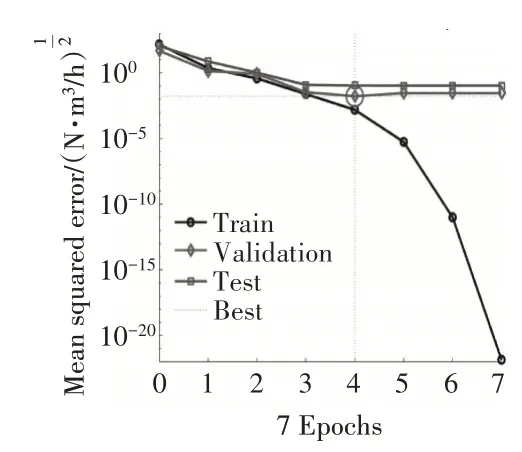
圖5 訓練次數與均方誤差的關系

圖6 預測值與樣本值的相關系數

2.3 泛化預測

根據訓練后的神經網絡預測的50組同時改變上下游保護間隙和刷絲排數時的泛化數據分別見表3、4。表3、4分別僅改變上下游參數，其它參數按表1取值。需要指出的是，基于訓練后的神經網絡，這些泛化預測數據幾乎是瞬間獲得的，而且理論上可以得到幾個參數的任何取值組合。這樣，基于神經網絡方法獲得CFD模型的泛化數據無論在時效性還是參數組合的適用性上都有很大優勢。

3 刷絲排數和保護間隙對泄漏率的耦合影響

刷絲排數和保護間隙對泄漏率的耦合影響如圖7所示。從圖中可見，無論是改變上游參數還是改變下游參數，泄漏率的大小和變化規律基本一致，也與直觀感受一致，即泄漏率隨著刷絲排數的增加而降低，隨著保護間隙的減小而降低。同時，也能發現保護間隙高度和刷絲排數影響具有一定的耦合性，隨著刷絲排數的增加，保護間隙對泄漏率的影響變弱；而隨著保護間隙的減小，刷絲排數對泄漏率的影響也變弱。這一耦合規律可以從分析影響泄漏率主要因素的角度理解，當刷絲排數增加到一定數量后，刷絲束區域的流動阻力足夠大，因此泄漏率對保護間隙的變化不敏感；而類似的，當保護間隙小到一定程度后，保護間隙區域的流動阻力足夠大，因此泄漏率對刷絲排數的變化不敏感。可見，雖然這里的泄漏率數據為神經網絡泛化數據，并不能從神經網絡的角度對規律進行解釋，但是這一泛化結果卻與從物理層面的解釋相吻合。

表3 同時改變上游保護間隙和刷絲排數時的泛化數據

表4 同時改變下游保護間隙和刷絲排數時的泛化數據

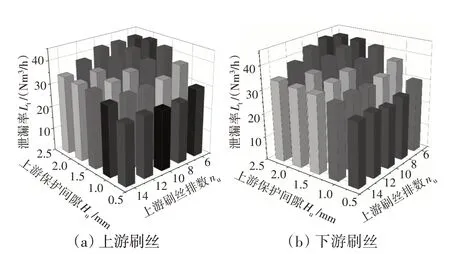
圖7 刷絲排數和保護間隙對泄漏率的影響

4 刷絲排數和保護間隙對級間不平衡性的耦合影響

級間不平衡用級間壓比表征，刷絲排數和保護間隙對級間不平衡的綜合影響如圖8所示。從圖中可見，與對泄漏率的影響不同，改變上游參數與改變下游參數對級間壓比的影響有較大不同。從整體看，下游參數變化對級間壓比的影響更明顯，最大值和最小值分別為3.61和0.41，而上游參數變化時級間壓比的最大值和最小值只有3.14和1.15。僅改變下游參數時，級間壓比隨著刷絲排數的增大而增大，隨著保護間隙的增大而減小；而僅改變上游參數時，級間壓比總體上（在保護間隙為1.1～2.3 mm時成立）隨著刷絲排數的增大而減小，隨著保護間隙的增大而增大，與改變下游參數時趨勢相反，這可以結合級間壓比的定義以及參數變化對流動阻力的影響理解這一規律。

圖8 刷絲排數和保護間隙對級間不平衡的影響

同樣，保護間隙高度和刷絲排數影響也具有一定的耦合性。僅下游參數變化時，隨著刷絲排數的增加，保護間隙對級間壓比的影響變弱；而隨著保護間隙的減小，刷絲排數對泄漏率的影響也變弱。而僅上游參數變化時，上述耦合性不明顯。上述耦合規律類似的可以從分析影響壓降主要因素的角度理解，另外由于壓降主要發生在下游刷式密封結構上，也可以解釋為什么下游參數影響的耦合性較強。同樣，雖然這里的級間壓比數據為神經網絡泛化數據，并不能從神經網絡的角度對規律進行解釋，但是這一泛化結果卻與從物理層面的解釋相吻合，也可以看出神經網絡適用于預測具有明顯耦合性的量級刷式密封流動。

最后，還可以從泛化數據中進行參數優選。當上下游保護間隙和刷絲排數分別為1.5、1.9 mm和10、8時，級間壓比為1.009，最接近1，這一取值組合可以消除級間不平衡，但對應的泄漏率較大，為41.894 N·m/h；而上下游保護間隙和刷絲排數分別為1.1、1.5 mm和14、10時，級間壓比為1.155，也很接近1，而且泄漏率只有30.688 N·m/h，這一取值組合可以基本消除級間不平衡，且密封性能較好。

5 結論

（1）文中建立的神經網絡訓練4次后，驗證數據和測試數據與預測值的均方誤差達到0.0169；訓練7次后，訓練數據與預測值的均方誤差小于10。訓練樣本與預測值滿足很好的線性關系，相關度系數達到0.99997。

（2）根據本文算例神經網絡的泛化預測數據，泄漏率隨著刷絲排數的增加而降低，隨著保護間隙的減小而降低；隨著刷絲排數的增加，保護間隙對泄漏率的影響減小；而隨著保護間隙的減小，刷絲排數對泄漏率的影響也會減小。

（3）根據本文算例神經網絡的泛化預測數據，下游參數變化對級間壓比的影響更明顯；僅改變下游參數時，級間壓比隨著刷絲排數的增加而增大，隨著保護間隙的增大而減小；而僅改變上游參數時，級間壓比總體上（在保護間隙為1.1～2.3 mm時成立）隨著刷絲排數的增加而減小，隨著保護間隙的增大而增大；僅下游參數變化時，隨著刷絲排數的增加，保護間隙對級間壓比的影響減小；而隨著保護間隙的減小，刷絲排數對泄漏率的影響也減小。而僅上游參數變化時，上述耦合性不明顯。

（4）上下游刷絲排數和保護間隙對泄漏率和級間不平衡性的影響雖然源于神經網絡泛化數據，卻與從物理層面的解釋相吻合，顯示了神經網絡適用于預測具有明顯耦合性的2級刷式密封流動特性。

（5）針對本文算例，上下游保護間隙和刷絲排數分別為1.1、1.5 mm和14、10時，級間壓比為1.155，泄漏率只有30.688 N·m/h，基本消除級間不平衡，且密封性能較好。

本研究尚有一些不足，例如神經網絡技術存在過學習或欠學習現象，對訓練數據的要求較高，可能對2級刷式密封流動的預測結果有影響。作者將針對以上不足開展進一步研究。