離子推力器內部等離子體的微觀特性研究

陳娟娟，耿 海，龍建飛，吳辰宸，賈艷輝，郭 寧

（1.蘭州空間技術物理研究所 真空技術與物理重點實驗室，蘭州 730000；2.南華大學，湖南 衡陽 421001）

0 引言

相比化學推力器，離子推力器具有推力小、比沖高、壽命長、推力連續可調等顯著特點[1]，在執行相同航天任務時可大幅節省航天器推進劑消耗量，提高有效載荷比。

離子推力器地面磨損試驗[2]和在軌飛行試驗[3~4]結果均顯示，推力器工作一段時間后其部分部組件會發生一定程度的磨損，包括離子光學系統[5~6]、磁極靴[7]、陰極孔[8]、陰極頂[9]、觸持極[10~11]、陰極管[12]等。離子推力器各組成部件和工作原理不同，導致不同部組件的磨損機制和影響因素也有很大差異。空心陰極作為離子推力器的關鍵部組件之一，其功能是為推力器氣體放電提供電子源。觸持極為空心陰極的一個組成部件，其作用一方面是維持陰極放電，另一方面是保護陰極管、陰極頂免受來自放電室內離子的轟擊腐蝕。NSTAR和NEXT長壽命試驗測量結果[8~12]顯示，推力器工作上萬小時后，陰極頂的外圍厚度只剩下最初的28%，質量減少了128 mg。致密的鎢微晶沉積在陰極孔周圍，平滑地從孔中心向外擴散，在孔壁表面的沉積厚度達到50μm。觸持極保護了陰極頂，使得陰極頂避免了由于離子濺射腐蝕導致的過早損壞，但當觸持極被磨損穿透后，陰極頂和陰極管便暴露在等離子體環境中，受到來自放電室內部高能離子的轟擊濺射刻蝕。長時間的轟擊濺射會使得觸持極發生磨損失效，嚴重時導致陰極壽命終止，推力器無法正常工作。因此，觸持極濺射是影響離子推力器工作壽命的一個關鍵因素。文獻[13]指出，導致觸持極頂磨損的最直接原因是高能離子對觸持極頂壁面的轟擊濺射刻蝕，而空心陰極出口附近混雜頻率下的大幅電勢脈動是觸持極高濺射能量的來源。文獻[14-21]試驗測試結果也證實，在觸持極頂附近確實存在大幅電勢脈動和徑向能量高達100 eV的高能離子（Xe++和交換電荷（CEX）離子[20]）。

針對這一問題，國內外均開展了大量的研究。其中最著名的是美國密歇根大學Gallimore等[22]提出的半經驗理論分析模型和美國推進實驗室（JPL）Mikellides等[23]提出的二維數值計算模型。半經驗理論分析模型是將試驗測量到的振蕩電勢作為已知量，通過追蹤一價和二價離子在振蕩電勢下的軌跡，統計進入陰極表面鞘層的離子個數，計算濺射產額，得到觸持極表面的腐蝕分布。二維數值計算模型是采用流體方法先得到放電室內的平均電勢，為引入離子聲波的影響，在試驗基礎上對離子聲波的電勢進行了模化以得到離子聲波對平均電勢的影響，進而分析不同脈動幅值下的觸持極腐蝕深度。國內，蘭州空間技術物理研究所的郭寧等[24]開展了不同工作模式下空心陰極的放電振蕩試驗測試，研究發現了陰極工作參數對陰極工作模式及陰極下游等離子體分布特性的影響。谷增杰等[25]利用空心陰極理論模型進一步分析了陰極工作參數對陰極內部不同區域放電電壓、發射體溫度等的影響；馮杰等[26]在陰極穩定自持放電后，在陽極板上施加一個瞬時大電流沖擊，檢測其對陰極本身放電特性的影響。Chen等[27]針對多模式離子電推進空心陰極開展了陰極工質流率裕度范圍和性能衰退試驗測試。北京理工大學的Qin等[28-29]采用試驗測試手段測量了不同陰極工質流率下的空心陰極下游電勢振蕩頻率和振幅，另外，他們用試驗測量的方法研究了環尖形陽極和平板型陽極，不同陰極工質流率、放電電流、放電電壓對陰極下游電勢振蕩頻率和振幅的影響[30]。

國外的研究是將放電室電勢振蕩和陰極濺射刻蝕過程進行解耦，國內的研究主要集中在空心陰極本身，但事實上空心陰極觸持極頂的濺射腐蝕是離子推力器長時間工作時高能離子對觸持極表面的轟擊引起的，它是空心陰極和放電室耦合作用下的結果。

本文提出了一種將經典力學和經典動力學結合的方法，采用假設位移條件，以位移為核心參考變量，建立離子推力器放電室內部電磁場、等離子體振蕩與位移之間的關系，并引入粒子碰撞模型，研究電磁場作用下的離子位移變化。采用級數理論給出等離子體振蕩是否收斂的證明，得到準平衡態的等離子體振蕩隨時間的演化方程。根據放電室氣體放電理論，得到放電室性能曲線。

1 數學解析模型

1.1 離子推力器放電室

圖1為一個典型的環尖場離子推力器放電室結構組成示意圖。本文期望采用解析的方法研究離子推力器放電室內部的等離子體動態行為，為此，建立了一個典型離子推力器放電室的數學解析模型。

圖1 典型的環尖場離子推力器放電室結構組成示意圖Fig.1 Schematic diagram of discharge chamber of typical ring-cusp ion thruster

圖中B表示放電室內的任意一個離子，其直角坐標系下的坐標分別用xB和yB表示，廣義坐標系下的坐標分別用r和θ表示；X、Y分別表示放電室的軸向和徑向方向；Xmax、Ymax分別對應軸向和徑向方向計算區域的最大值。

1.2 離子動能

B點直角坐標系坐標（xB，yB）和廣義坐標系坐標（r，θ）之間的轉換關系為：

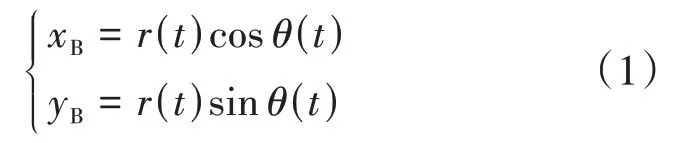
式中：t為放電室工作時間。

離子速度為：

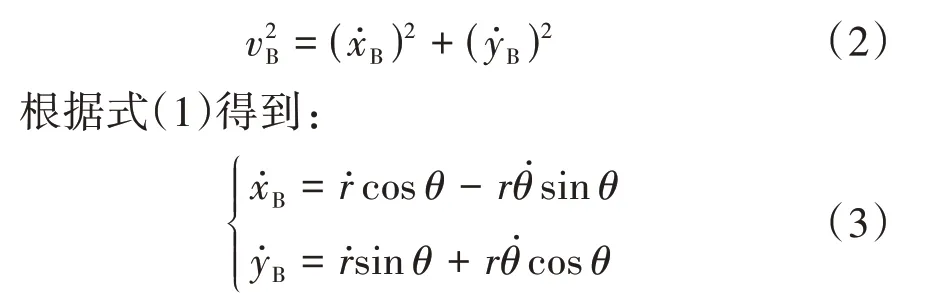
式中：x?B和y?B分別表示B點離子在直角坐標系中的軸向和徑向速度。

將式（3）代入式（2），得到質點B離子速度：

式（4）中離子速度由廣義坐標決定。由式（4）得到質點B的離子動能TB：

式中：mi為離子質量。

1.3 離子勢能

離子勢能V是與廣義坐標有關的函數：

1.4 拉格朗日方程

聯立式（5）和式（9），得到離子的拉格朗日方程：

進而得到：

式中：C1、C2均為常數。將初始條件代入式（19），得到常數C1=0。

C2為德拜球內離子最大位移，即德拜長度；β為等離子體振蕩頻率，它與離子密度、真空介電常數、粒子質量有關。

1.5 粒子碰撞模型

圖2為質點系中質點B的碰撞模型。

圖2 粒子碰撞模型Fig.2 Particle collision model

放電室氣體內部粒子由離子、中性原子和電子組成。離子運動過程中受到中性原子和電子的碰撞，假設電子、中性原子和離子的運動速度分別為ve、v0、vi。

首先考慮一個粒子與離子的碰撞過程對離子運動的影響。如圖3中B為離子，A為任意一個粒子。B離子的廣義坐標為（OB，θ1），A粒子的廣義坐標為（OA，θ2）。參考點0點為OB=0、OA=0、θ1=0、θ2=0對應的點。

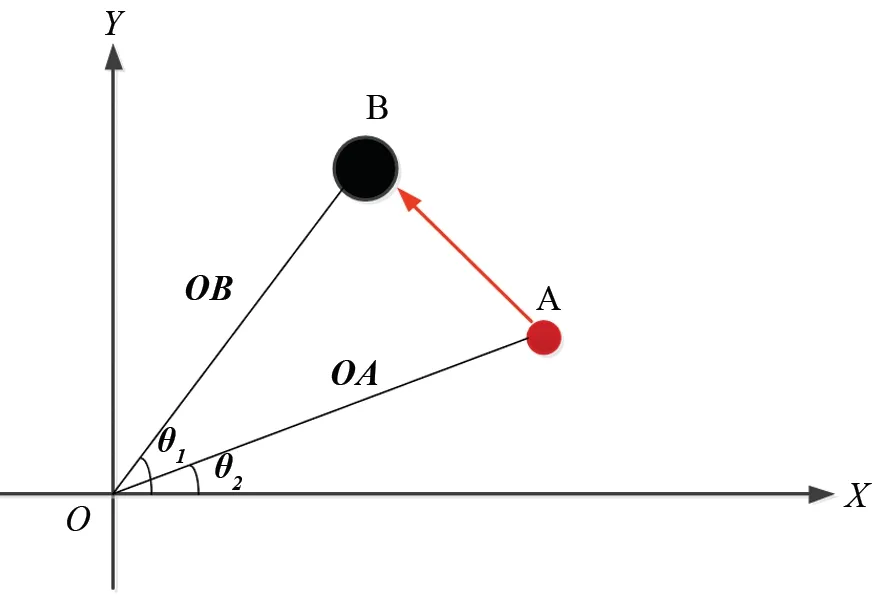
圖3 粒子間碰撞Fig.3 Collision between particles

B離子的位置坐標和速度分別滿足式（23）、（24）。B離子位置：

圖3中，運動的B離子受到運動的A粒子的碰撞，這里僅考慮B離子受到A粒子碰撞后其廣義坐標的變化情況。

OA、OB系統的動能為：

式中：F為粒子A受到的作用力；E為電場強度；B為磁感應強度；Δt為力的作用時間。

電子、中性原子、離子對應的沖量分別為Ie、I0、Ii，根據式（33）分別得到電子、中性原子和離子的沖量表達式為：

離子推力器放電室內部，電子的運動速度遠大于中性原子和離子的運動速度，即Ie＞＞I0、Ie＞＞Ii，因此在電場強度、磁感應強度一定的情況下，電子、中性原子和離子與運動的離子發生碰撞時，離子受到的最大沖量來自電子。

給θ1一個變分，保持θ2不變，離子的廣義力?θ1可表示為離子沖量Ii和離子位移OB之間的關系：

將式（33）代入式（39），得到：

式（40）即為碰撞后的離子旋轉角度微分方程。

1.6 等離子體振蕩模型

當放電室內的等離子體偏離電中性時，靜電力就會對帶電粒子產生作用，作用的方向使等離子體恢復電中性，因而靜電力就起到了一種恢復力的作用。又由于帶電粒子本身有質量，在恢復力的作用下，等離子體會發生振蕩，這是粒子運動與電場耦合所產生的必然現象。

對于離子推力器而言，一般在鞘層區域會出現等離子體電中性偏離。假設鞘層厚度為d，離子溫度為0，則在該鞘層內產生一個電場

式中：vth為離子熱速度。

通常，離子推力器放電室內部離子溫度不為0，因此，在受力方程中會出現一個由離子壓力梯度產生的項。當Ti≠0時，式（44）描述的等離子體振蕩轉變成等離子體波。在無磁場且碰撞不重要時，有：

式中：γ為絕熱因子。

假設離子密度、電場和離子速度在放電室徑向y方向分別有一個小的圍繞項n1、E1、v1：

等離子體中，沒有零階電場，也沒有零階漂移運動，因此所有物理量將按照正弦波變化：

式中：ky為傳播常數；ω為等離子體靜電波頻率。

通常在波頻率的時間尺度上離子基本上是靜止的，其物理量按照式（46）～（49）變化，將式（46）～（49）代入離子連續性方程、受力方程和散度方程，得到如下一階方程組：

2 結果分析及討論

圖4為離子和電子拉莫爾半徑（m）隨磁感應強度（T）的變化曲線。圖中藍色曲線代表電子、紅色曲線代表離子。結果顯示，不管是電子還是離子，它們的運動軌跡均會受到磁場的影響，由于電子質量較輕、運動速度較大，因而受到的磁場約束比離子大得多。

圖4 粒子的拉莫爾半徑隨磁感應強度的變化Fig.4 Larmor radius of particle varies with the magnetic induction intensity

圖5為電子運動軌跡示意圖。

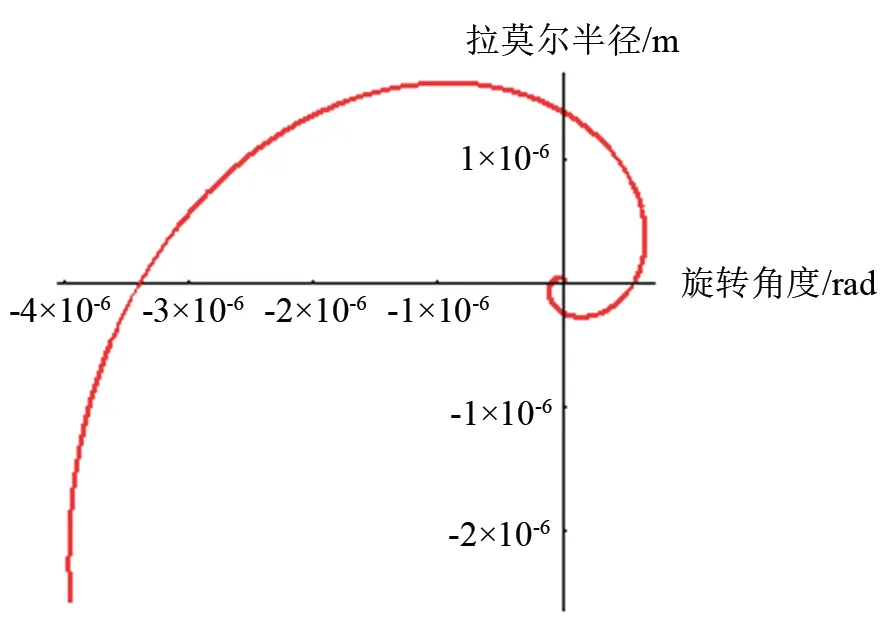
圖5 電子運動軌跡示意圖Fig.5 Sketch of electron trajectory

圖5結果顯示，受到磁場的影響，電子做螺旋運動。圖6給出了利用數值仿真計算得到的磁場約束作用下的電子運動軌跡，結果同圖5，即電子在磁場作用下做螺旋運動。

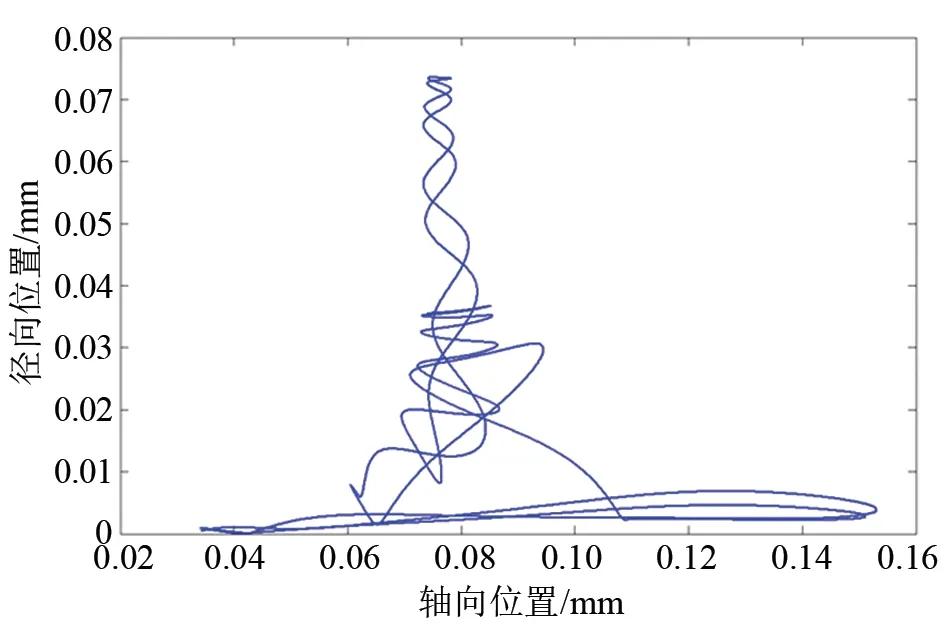
圖6 電子運動軌跡數值仿真結果Fig.6 Simulated electron trajectory

圖7為沒有碰撞的情況下單個離子位移隨時間的變化曲線（橫坐標時間為歸一化值，位移單位為m）。

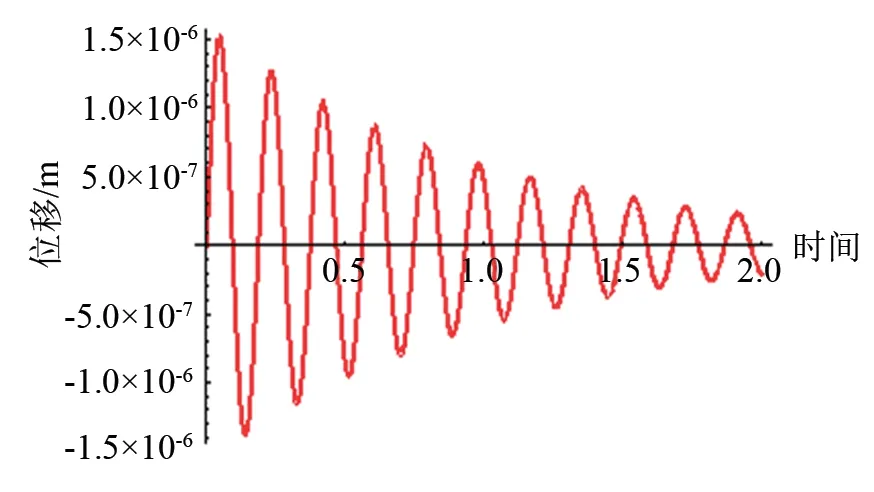
圖7 單個離子位移隨時間的變化曲線Fig.7 Displacement of a single ion varies with the time step

從圖7可以看出，在很短的時間內離子位移發生類似于正弦函數的振蕩分布，只是振蕩幅值發生變化，隨著離子的運動，幅值越來越小，最后趨于穩定。根據等離子體振蕩理論可知，在一個德拜球內，離子的熱運動對等離子體的整體運動行為有很大的影響，朗道阻尼的存在導致振幅隨時間衰減。

事實上，離子在很短時間內的位移振蕩與等離子體密度有關。圖7是離子密度為1.0×1016m-3時的離子位移計算結果。

圖8為離子密度分別為1.0×1017m-3、1.0×1015m-3時的離子位移隨時間變化曲線。

對比圖7、圖8可以發現，離子密度對離子的位移振蕩頻率影響非常大，對振蕩幅值的影響不明顯。離子密度越大，等離子體振蕩頻率越高，這點由等離子體振蕩頻率與離子密度的關系表達式（20）可知。

圖8 離子位移隨時間的變化曲線Fig.8 Displacement of ion varies with time step

圖9為等離子體振蕩頻率隨離子密度的變化曲線。從圖可以看出，等離子體振蕩頻率確實與放電室內的離子密度有關，離子密度越大等離子體振蕩頻率越高。分析圖9發現，離子密度增加一個數量級，等離子體振蕩頻率增大5倍，這對離子推力器是極其不利的。

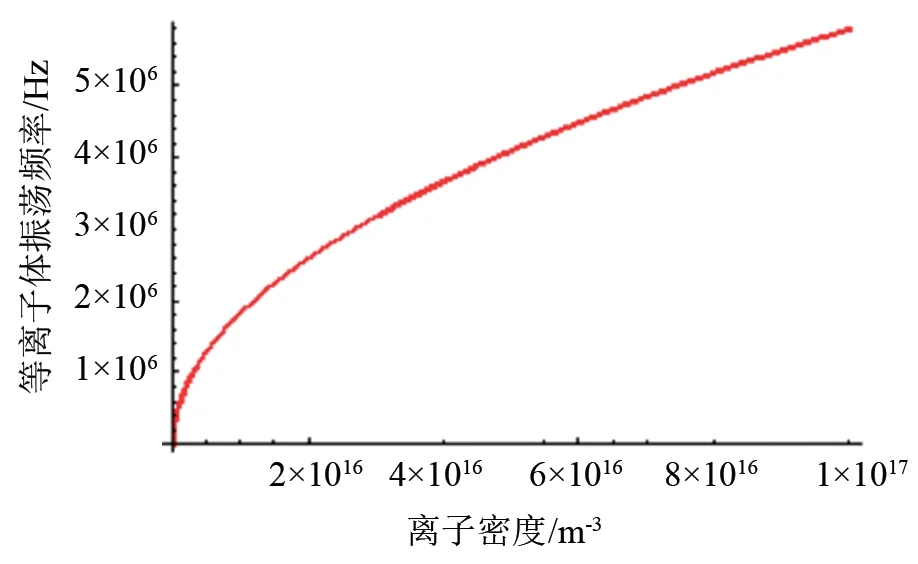
圖9 等離子體振蕩頻率隨離子密度的變化曲線Fig.9 Variation of the plasma oscillation frequency with the ion density

須盡量使放電室內部離子的密度足夠高，同時等離子體振蕩頻率非常小，才有可能保證推力器長期可靠運行。因此在設計推力器時必須折中考慮推力器的性能和壽命。

圖10為沒有碰撞情況下離子旋轉角度增量隨時間的變化曲線。

圖10 離子旋轉角度增量隨時間的變化曲線Fig.10 Increase of the ion’s rotational angle varies with the time step

計算結果顯示，離子運動過程中不僅位移有變化，運動角度也發生了變化。分析認為這是由于離子推力器放電室內鞘層區離子的熱運動和擴散運動導致的。離子質量非常大，磁場幾乎不會影響它的運動行為。從計算結果看出，擴散引起的離子旋轉角度的增量僅為10-12rad，這意味著熱運動和擴散引起的離子旋轉角度變化很小。

求解式（40），得到與電子碰撞后的離子旋轉角度θ1的表達式：

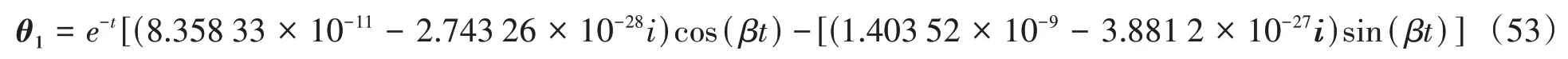
圖11為考慮粒子間碰撞后的離子旋轉角度隨時間的變化。結果發現，當離子受到快速運動的電子碰撞后，其旋轉角度約為10-10rad，結合電子和離子的彈性碰撞截面[31]可知，離子的運動方向受到電子碰撞的影響，因此若要提高離子推力器放電室內部離子的分布均勻性，可以通過提高電子和離子之間的碰撞概率來實現，但碰撞概率的提高會降低碰撞電子的能量，減小中性氣體的離化概率，因而，在設計離子推動器產品時須折中考慮離子的分布均勻性和中性原子的離化率。

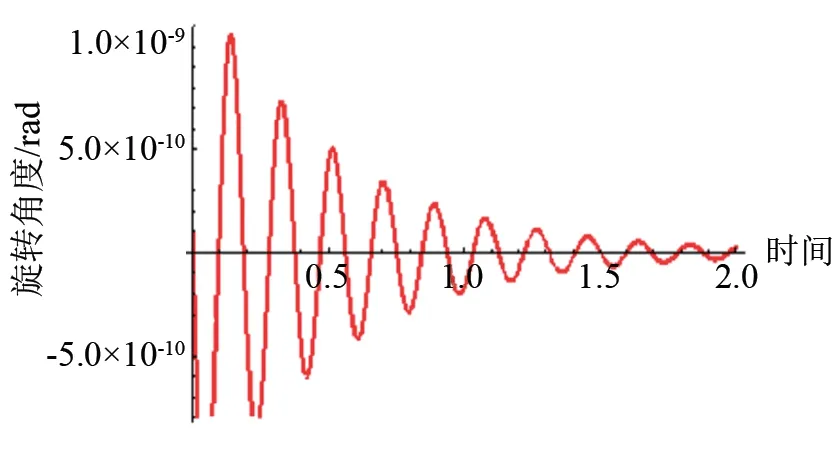
圖11 離子旋轉角度隨時間的變化曲線Fig.11 Variation of ion’s rotational angle with time step

圖12是不同的磁感應強度下離子旋轉角度隨時間的變化曲線。

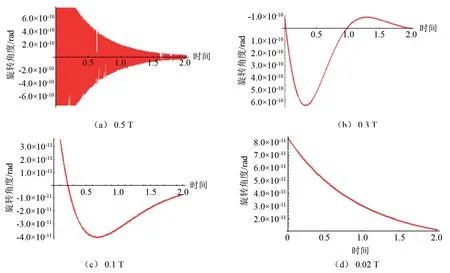
圖12 磁感應強度對離子旋轉角度的影響Fig.12 The effect of magnetic field on the ion’s rotational angle

從圖12計算結果可以看出，放電室內的磁感應強度對離子運動軌跡的影響非常大。圖12（a）表明，磁感應強度較大時，離子的旋轉角度較大，且隨著時間發生正負變化，即繞著磁力線左右旋轉；當磁感應強度從0.5 T減小至0.1 T時，離子的旋轉角度減小，但仍然繞著磁力線左右旋轉，如圖12（b）和（c）所示；但是當磁感應強度為0.02 T時，離子的旋轉角度均為正值，意味著此時離子僅沿其磁力線做一個方向的旋轉。

離子推力器放電室內陽極壁磁體附近的磁感應強度最強，約為0.5 T，在該磁場約束下，運動速度較快的電子很快到達陽極壁附近，并在陽極壁兩磁極之間的磁鏡效應作用下做往復運動，大量帶負電的電子聚集在陽極表面形成負電位，使放電室內的等離子體呈電中性偏離；運動速度較慢的離子在陽極壁附近和帶負電位的電子之間形成了鞘層，由于電勢差的存在，鞘層之間出現了使離子運動速度加快、電子速度放慢的電場，在該電場作用下離子加速運動，并與其他粒子發生碰撞。由于電子沿磁力線往復運動，與離子的碰撞會導致離子發生方向不恒定的角度偏轉。另外，在該鞘層區域內，由于離子密度差異較大，離子在電場作用的同時，還會有擴散運動。因而出現圖12（a）～（d）所示的結果。

放電室內部磁感應強度非常小，離子幾乎只受到電場的作用和其他粒子的碰撞，事實上在放電初期，離子的旋轉主要來自于其他粒子的碰撞，但是隨著氣體放電的穩定，放電室內部等離子體處于準中性狀態，離子的旋轉角度隨著放電的進行逐漸減小，當放電達到穩定，整個等離子體處于穩態時，離子將不再做旋轉運動。

圖13是不同的電場強度對離子旋轉角度增量的影響。結果顯示，放電室內的電場強度對離子的旋轉角度影響很大，當電場強度由1.0×105V/m變為1.0×103V/m時，離子的角度旋轉增量從1.4×10-5rad減小至3.2×10-6rad。

圖13 電場強度對離子旋轉角度增量的影響Fig.13 The effect on the electric field on the ion’s rotational angle

離子推力器放電室內部的電場來自兩部分，（1）陰極和陽極之間的電勢差引起的靜態電場；（2）運動的等離子體產生的動態電勢。一般情況下，運動等離子體產生的動態電勢比靜態電場小得多，因此等離子體基本只受到靜態電場的影響。放電室內的電勢呈現中心強邊緣弱的分布特點，因而不同區域的離子受到的靜電力也會隨之改變。

結合式（51）和式（21），得到考慮粒子碰撞后等離子體振蕩下的離子位移：

根據級數理論可知，當離子推力器中存在大量離子時，等離子體整體運動的位移為：

傅里葉級數f(t)存在間斷點π/2ωn，在該點處級數收斂。因此，根據狄利克雷條件得到傅里葉級數收斂值為：

由式（56）可知，有大量離子的等離子體的運動位移在間斷點處收斂，即此時等離子體運動達到了準平衡。

將式（55）代入式（10）離子拉格朗日方程，得到非平衡態時的離子含時演化方程：

求解式（57）可得到準平衡態時的等離子體動態特性曲線：

將結果代入離子推力器放電室理論模型中，計算得到離子推力器放電室的性能曲線，如圖14所示。

圖14 放電室性能曲線Fig.14 Performance curve of the discharge chamber

結果表明，雖然離子推力器放電室內部陰極下游存在等離子體電勢振蕩，但該振蕩不會影響離子推力器放電室的性能。圖14計算結果符合離子推力器放電室設計要求。根據試驗測量結果，得到離子推力器放電室性能表達式：

式中：ηm、ηd分別為工質利用率和放電損耗。

3 總結

大量的在軌飛行測試和地面試驗測量結果表明，離子推力器長時間工作后空心陰極觸持極會受到大量來自放電室內高能離子的轟擊，分析認為，這是由于陰極下游出現了大幅度等離子體振蕩所致。本文針對離子推力器空心陰極觸持極的轟擊濺射問題，采用理論分析方法從機制層面逐一分析等離子體密度、粒子間碰撞、磁感應強度和電場強度對等離子體振蕩的影響，結果顯示，以上幾個因素都會影響等離子體的運動行為，其中，等離子體密度和磁感應強度的影響程度較大。為了降低觸持極的濺射刻蝕速率，提高空心陰極工作壽命，必須降低陰極下游的等離子體密度和磁感應強度。后續離子推力器優化設計時須在保證磁等勢線閉合且放電室內無磁場區較大的情況下，通過減小陰極附近的磁極個數來減小磁感應強度，使電子從陰極發射出來后進入放電室內，快速沿著磁力線朝屏柵方向運動，降低陰極下游的等離子體密度。