基于神經網絡的電力系統二次設備監測方法研究

史新新

（國電南瑞科技股份有限公司）

0 引言

二次設備作為智能電力系統的重要組成部分，承擔著對電力系統一次設備進行監測、控制、保護的任務，與電力系統中的電能并不發生直接關聯關系[1-2]。二次側設備主要包括電壓表、電流表、功率表等，主要負責采集一次側設備的運行數據，由此判斷智能電力系統的運行狀態[3-4]。二次設備數量的大幅度增加，對一次設備監測的準確性造成一定程度的影響。本文基于神經網絡模型對二次側設備采集到的運行數據進行分析，通過調整權值和閾值，有效剔除冗余數據，實現監測精度的提高，并且能夠對電力系統出現的異常情況進行快速的診斷，由智能電力系統做出相應的動作，保證電力系統的安全、可靠、穩定運行[5]。

1 二次設備數學分析

1.1 監測設備相關參數分析

監測設備相關參數包括電壓參數θ1、電流參數θ2、功率參數θ3、溫度參數θ4等，由于上述監測設備相關的參數單位是完全不同的，因此需要進行統一的標準化處理[6-7]，具體的處理方法為：

式中，Umn為進行過統一標準化處理后的參數；θmn為電流、電壓等相關參數；為θmn的平均值；σmn為θmn的方差值；U為參數的數量。

1.2 監測數據優化方法

為了對監測數據進行更有效的優化，需要對數據進行聚類處理，實現數據量的簡化。不同類型數據通過調整其歐式距離參數來調整聚類的具體標準[8]。本文在此基礎上進行優化，提出輪廓系數的概念，基于K-means方法，設定聚類中心，實現監測數據的聚類處理，并對不同類型數據的聚類等級SE進行合理劃分，完成監測數據的優化[9]，其中聚類中心診斷公式為：

式中，m為研究對象樣本中的個體；Q(m)為樣本個體在整個聚類中的最大距離，K(m)為樣本個體在本體聚類帶其他聚類的最小距離[10]。不同類型數據所對應的聚類在全部數據中的聚類等級計算公式為：

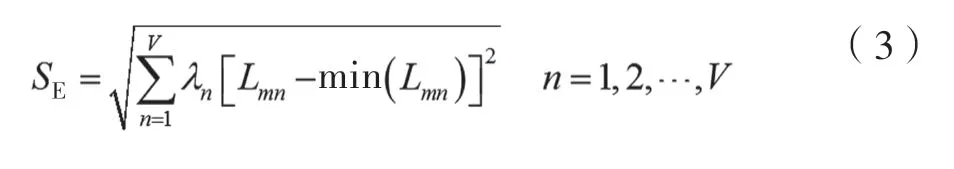
式中，λn為權重參數，全部的權重參數之和為l；Lmn為不同類型數據的聚類樣本；min(Lmn)為聚類樣本的中心；SE為全部的聚類中心到最小聚類中心的距離，離得越近，重要性等級越高。最后根據SE的大小排列，實現聚類數量的確定。

2 神經網絡模型

2.1 神經網絡

BP神經網絡中，信息從輸入層導入，逐級傳輸到輸出層，輸出層上生成的誤差再反向傳輸到輸入層[11]。BP神經網絡的結構如下圖所示。

圖 BP神經網絡拓撲結構

節點采用Sigmoid函數來描述，即：

2.2 模型數據運算

二次設備經過神經網絡模型的輸入層，進入到中間層處理，最終從輸出層導出，在數據進行反向傳輸時，中間層會根據閾值和權值參數對數據進行判斷，對于不符合要求的數據則剔除掉。將二次側設備研究對象樣本描述為RU=(R1,…,Rv)，中間層數據描述為SU=(S1,…,Sw)，輸出層數據描述為TU=(T1,…,Tl)，輸出結果診斷向量為DU=(D1,…,DL)；輸入層與中間層之間的權重參數為λmn=(m=1,…,v;n=1,…,w)，閾值參數為βmn=(m=1,…,v;n=1,…,w)；中間層與輸出層之間的權重參數為λnl=(n=1,…,w;l=1,…,h)，閾值參數為βnl=(n=1,…,w;l=1,…,h)。由此便可以得到神經網絡的正向傳遞公式為：

再根據輸出結果診斷標準得到輸出誤差，及輸出結果與理論結果之間的差異：

2.3 閾值分析

神經網絡運算的目的就是要實現輸出結果與理論結果之間的誤差最小化，因此需要通過泰勒展開公式e[ε(n+1)]對神經網絡模型中的閾值參數和權值參數進行優化，運算公式為：

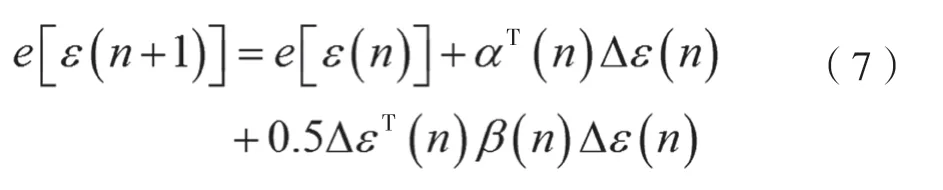
式中，α(n)為誤差在梯度方向上的分量；β(n)為海森矩陣，假設存在△ε(n)=-β(n)-1α(n)，就會得到誤差的最小值，海森矩陣的復雜程度直接對運算速度造成影響，如果存在雅可比矩陣β=JTJ且α=JTe，則泰勒展開公式就能夠簡化為：

2.4 歸一化運算

為了將數據的其他屬性對樣本的影響程度降到最低，將數據樣本進行歸一化處理，統一變換到 (0,1)區間內，其變換公式為：

式中，ρi為樣本中的任意數據；λ為歸一化運算后的結果；ρmax為樣本中數值最大的數據且無限趨近于1；ρmin為樣本中數值最大的數據且無限趨近于0。

2.5 誤差分析

二次設備的監測誤差可以劃分為兩種，即相對誤差ηX和方差ηF：

這兩個誤差參數能夠分別反映出進行優化后的數據情況和實際的數據情況，并且通過對這兩個誤差參數的合理運用到閾值參數和權值參數的調節，誤差分析能夠更有效、更準確地對數據進行科學的分析，有效地判斷二次設備數據監測的效果。

3 實例分析

3.1 監測樣本描述

以某地區的電壓表和電流表為例，分析神經網絡算法對二次設備監測的優化效果。神經網絡的輸入為電壓、電流、電功率、溫度，對上述數據進行監測，得到聚類輪廓，如表1所示。

通過對表1中數據進行分析發現，存在不同輸入變量的聚類系數和聚類分類數，當聚類等級值為5的時候，整個聚類的聚類系數最大。以此為基礎展開相關分析，確定聚類中心和聚類樣本，具體數據如表2所示。

表1 聚類輪廓參數表

表2 聚類中心和聚類樣本數據表

分析數據發現試驗頻率為110時，聚類效果最佳，后續功能測試都基于110進行。

3.2 二次設備監測精準度

分別在0.1、0.01、0.001三種精度要求下，對各個數值的精準度進行計算，得到的計算結果如表3所示。

表3 不同精度要求下的誤差數據表

由表3數據可知，在不同的精度要求下，計算得到的方差和相對誤差都能夠控制在合理的區間內，沒有明顯差別。

3.3 二次設備的運算時間

對二次設備的運算效率的研究，要基于不同的迭代次數展開，具體的運算數據如表4所示。

通過對表4數據進行分析可知，在迭代次數為1～100下，計算時間最長不會超過46s，運算數量最大為162。總體上來看，神經網絡方法對二次設備監測的優化效果比較好，能在較短的時間內對多個樣本數據進行監測，迭代次數為1～100下能夠將運算精度保持在98%左右。

表4 二次設備運算時間數據表

4 結束語

本文將神經網絡算法應用到電力系統二次設備監測優化中，通過對電力系統中電壓、電流、電功率、溫度等數據的監測，對理論監測數據與實際監測數據之間的誤差進行深入分析與研究，測試結果表明，在不同的精度要求下，計算得到的方差能夠控制在2.0左右，相對誤差能夠控制在1%左右；并且在進行運算時，迭代次數為1～100的情況下，運算時間最長不超過46s，運算精度能夠控制在98%左右，運算數據能夠達到162個。

經過本文的深入分析可知，采用神經網絡方法對電力系統中二次設備監測數據進行優化，通過確定樣本數據中心，配置合理的閾值參數和權值參數等有效方法，對輸入到神經網絡中的數據進行反復的迭代運算，最終得到符合實際情況的數據。由此能夠達到二次設備對電力系統進行高效率監測的目的。