單頻雙差LM-BP神經網絡GNSS周跳檢測與修復研究

梁凌峰

（河南理工大學 測繪與國土信息工程學院，河南 焦作 454000）

0 引 言

在現代全球衛星導航定位系統（GNSS）的載波相位測量中由于衛星和接收機電子元件受電離層、對流層等外界環境影響，載波相位整周計數發生錯誤導致出現周跳現象。周跳如果不能被及時發現處理，將會嚴重影響定位結果。目前針對單頻GNSS數據中周跳的探測與修復方法很多，在眾多方法中多項式擬合法因其算法簡單，適用于計算機編程等特點，被廣泛使用。多項式擬合法原理是利用擬合計算載波相位序列值來探測周跳，以擬合曲線與測量值曲線的一致程度為標準，判斷該異常重合點是否為周跳。然而由于其方法常應用于無差觀測量，直接利用原始載波相位可能會因其他觀測噪聲及誤差影響周跳探測修復精度。因此有必要尋求新的方法來改善周跳探測與修復效果。鑒于此本文提出一種基于雙差檢測量的LM-BP（Levenberg Marquardt-Back Propagation）神經網絡的探測修復周跳改進方法：將構建差分數據和改進擬合算法相結合，從而實現單頻數據周跳探測與修復精度的提高。在數據方面，考慮到雙差觀測值消除了鐘差，且在短基線情況下，電離層及對流層延遲、軌道誤差等均得到大幅度削弱，僅剩下影響較小的多路徑誤差和觀測噪聲，所以雙差觀測有利于小周跳的探測；在擬合算法方面，人工智能領域中采用LM算法的BP神經網絡由于其出色的數據擬合與預測能力被廣泛應用于土木工程、化工、導航等領域，可以考慮采用神經網絡替代多項式擬合算法，以達到精度提升的目的。

該方法利用了LM-BP神經網絡的誤差逆向傳播學習以及自動調整擬合過程中權值的特性，和雙差檢測量對于不易受其他測量誤差影響的特點，從而提高了周跳探測與修復的精度。最后運用實測數據與傳統多項式擬合方法對比分析，驗證了該方法在周跳探測與修復精度上的提升。

1 基于LM算法BP神經網絡周跳探測修復模型

1.1 基于載波相位雙差虛擬觀測量的BP數據集

設時刻、兩顆衛星在1、2號測站同時觀測，則、星兩衛星載波相位觀測值的雙差觀測方程為：

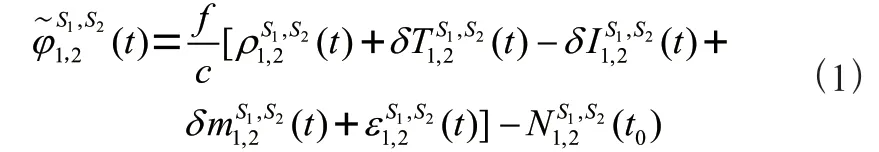
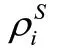
從上式可知，由于觀測量的時空相關性特點，電離層和對流層延遲影響、多徑效應、高頻噪聲影響已被大幅削弱，對于測站基線較短的觀測問題，這些誤差影響可以減小到忽略不計。因此，采用載波相位雙差檢測量作為BP神經網絡輸入層數據集，可以確保探測小周跳的敏感性。

1.2 基于LM-BP的周跳探測修復模型

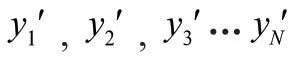
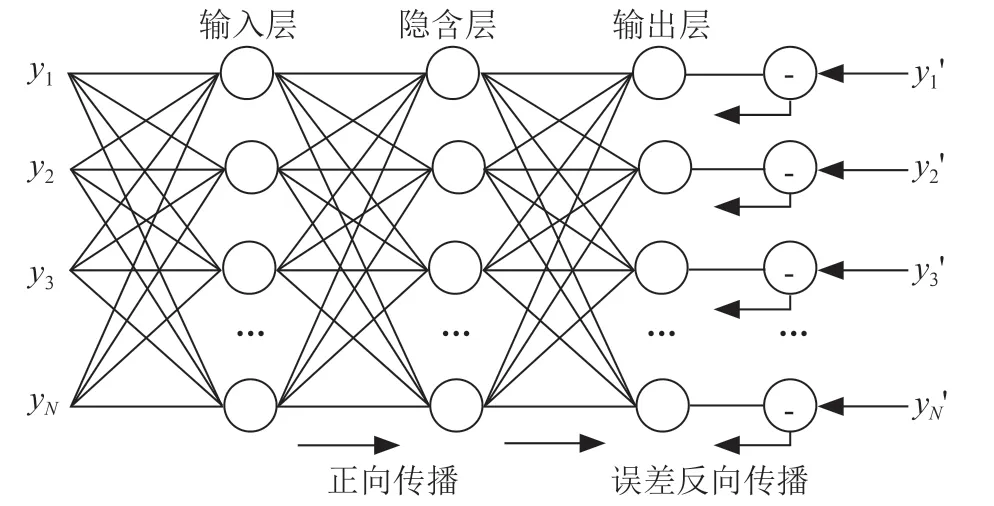
圖1 BP神經網絡結構圖

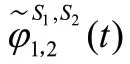
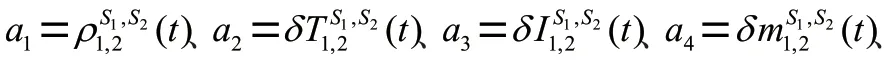
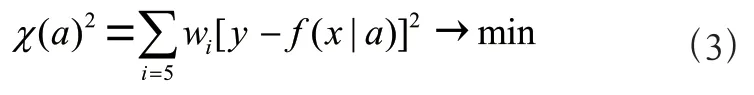
式中：()表示關于向量的一個超曲面，w=1/δ，表示觀測量所對應的權值。

設待優化向量擬合步長為Δ，文獻[8]，將誤差超曲面(+Δ)線性化，取其一階和二階項，得到其矩陣形式：

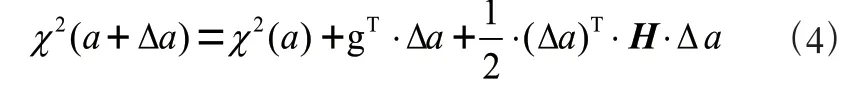
式中：為多維空間中梯度向量，為海森矩陣。

為了使(＋Δ)取極值，需要更新向量Δ，以使(＋Δ)在該點處的梯度等于零。根據式（7）可有：

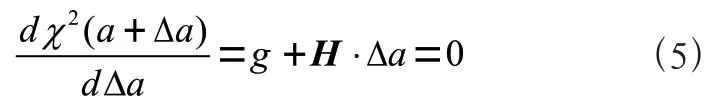
可進一步得到向量與矩陣的矩陣表達式：

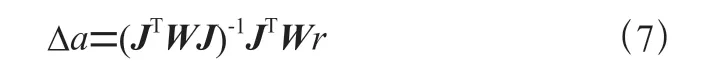
LM算法結合了梯度下降法和高斯—牛頓方法兩者的優勢，引入了阻尼因子控制梯度步長，從而提升計算參數向量的效率，參考文獻[9，10]，可以將式（7）改進為LM-BP算法：

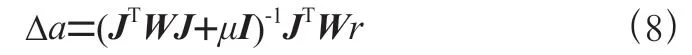
式中：為單位矩陣，當系數為0時，式(8)為牛頓法，當系數的值很大時，其變為步長較小的梯度下降法。當每次迭代后，如(+Δ)增加，拒絕本次迭代，并增加阻尼，從而減小了步長Δ，進行下次迭代，確保迭代過程始終往目標函數的“下坡”方向進行。

迭代完成后最終可得到最佳參數向量，將其帶入模型函數ˊ=(|)，得到擬合后各歷元的載波相位雙差虛擬觀測值ˊ()。當發生周跳時，衛星雙差檢測量會產生相應大小的突變，因而將擬合檢測量ˊ()與實際檢測量()求差得到擬合殘差，根據其中誤差設立閾值來判斷周跳是否發生，此處的中誤差為：

式中：v為參數向量對應的擬合殘差，為參與擬合歷元數，為擬合參數個數。

可設定周跳探測的閾值為3，若發生周跳，擬合值與實際的觀測值殘差絕對值大于閾值，則有下式：

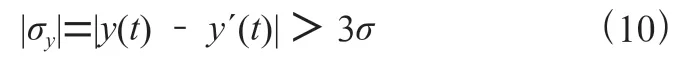
在以上理論模型的研究基礎上，圖2為探測修復周跳的流程。

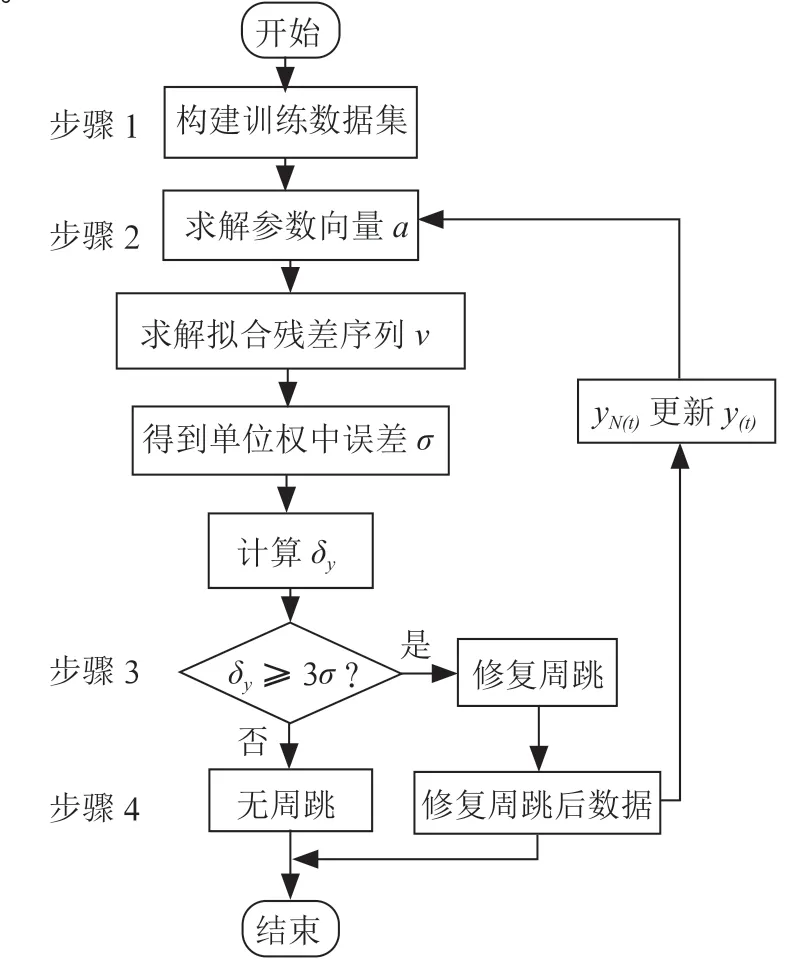
圖2 探測修復周跳流程圖

結合流程圖，總結基于LM算法BP神經網絡周跳探測修復的主要步驟為：

步驟1：通過原始雙差觀測序列()，構建LM-BP神經網絡訓練數據集y()。

步驟2：利用數據集y()求解LM-BP神經網絡模型的最優參數向量，求解擬合殘差序列，得到單位權中誤差。

步驟3：求解下個相鄰歷元的擬合觀測量ˊ()，求解σ，若|σ|滿足式(10)條件，則將該歷元對應的觀測量()替換為BP神經網絡數據集y()的擬合出的歷元觀測量，得到修復周跳后的數據；若不滿足條件，則視為無周跳。

步驟4：得到無周跳數據，若數據是周跳修復后的數據，則自動轉入步驟2，以該數據更新數據集()，作為下一歷元周跳檢測的依據，依次循環。

2 實驗與結果分析

為驗證算法的正確性和有效性，于2020年10月21日，在河南理工大學某建筑物樓頂的測試臺設1、2號測站（兩測站間距為150 cm），利用2臺SR1千尋星矩測地型GNSS接收機進行同步靜態數據采集，采樣間隔為1 s，連續觀測85 min。篩選出無周跳的原始觀測數據并計算站間星間雙差值。

經測試，本次實驗取最佳情形下參數設置：多項式擬合法中階數取為4階；LM-BP神經網絡中，隱含層數為50層，對輸入數據集使用隨機劃分數據方法，設置訓練子集、驗證子集和測試子集的比例為0.7:0.15:0.15。將雙差序列分別使用多項式法、神經網絡法程序進行處理，得到檢測殘差序列如圖3所示。

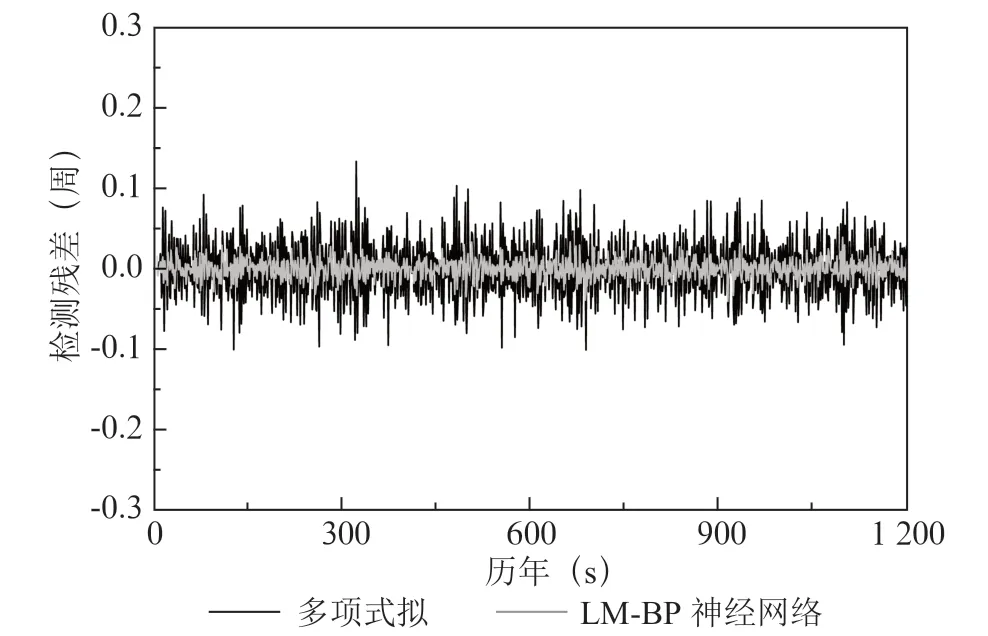
圖3 兩種方法無周跳情況下檢測殘差序列對比

由殘差序列可知，當無周跳發生時，兩模型的一步預報殘差均小于1。同時，對上述殘差序列進行統計分析，在數據歷元數從1 s增加到1 200 s過程中，得到多項式檢測殘差的平均中誤差為=0.052，LM-BP神經網絡檢測殘差的平均中誤差為=0.015。因此，LM-BP模型周跳探測的靈敏性優于多項式擬合法。

為驗證LM-BP神經網絡模型探測周跳的可行性，人工在雙差序列某些歷元中加入-2～15不等大小的周跳。將新方法與其他兩種傳統方法對比。最終處理結果如圖4所示。圖4給出兩種方法探測和修復后的殘差結果，可以看出，人工隨機添加的周跳均被探測出。其中，最小周跳為1周，多項式擬合探測結果為0.964周，與真實值相差-0.036周，神經網絡探測結果為1.009周，與真實值差值為0.009周；最大周跳為15周，多項式擬合探測結果為14.937周，與真實值相差-0.027周，神經網絡探測結果為14.982周，與真實值差值為-0.018周。說明LM-BP神經網絡法對于小周跳和大周跳都有良好的探測與修復效果。多項式擬合法探測周跳與真實值誤差范圍在±0.082間，神經網絡法的誤差范圍是±0.036，LM-BP神經網絡方法的精度優于多項式擬合法。

3 結 論

本文提出一種基于雙差檢測量的LM-BP神經網絡的探測修復GNSS周跳方法，利用LM-BP神經網絡的誤差逆向傳播學習以及自動調整擬合過程中權值的特性，和雙差檢測量對于不易受其他測量誤差影響的特點，提高了周跳探測與修復的精度。實驗結果表明：基于雙差的LM-BP神經網絡的周跳探測與修復模型能夠探測出GNSS雙差相位觀測值序列中小至1周的周跳，并能準確對其進行修復。且對于小周跳，神經網絡相比多項式擬合法精度更高。

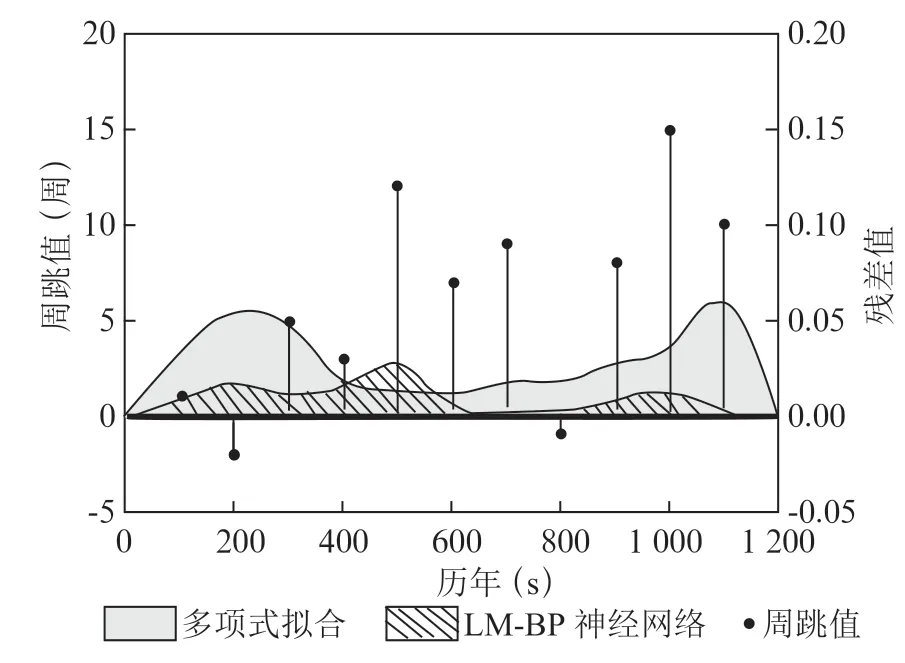
圖4 實測數據周跳探測結果

利用GNSS載波相位雙差作為檢測量進行周跳探測時，很難直接確定哪個原始相位觀測值發生周跳，如何結合其他方法快速地判斷確定之是我們下一步的主要研究工作。