基于CNN-GRU的瓦斯濃度預測模型及應用*

劉 超，雷 晨，李樹剛，薛俊華，張 超

(1.西安科技大學 安全科學與工程學院，陜西 西安 710054；2.西部礦井開采及災害防治教育部重點實驗室，陜西 西安 710054)

0 引言

煤炭是我國一次性能源消費的重要支柱，影響國內經濟發展和能源安全[1-2]。頻發的礦井瓦斯災害，給煤炭行業造成重大損失并嚴重威脅人們生命安全。目前，大部分煤炭企業已經配備成熟的安全監測系統，但其功能僅限于短期識別和應對災害，未能充分利用現有監測數據，導致礦井瓦斯災害預測能力不足。因此，迫切需要引入新的方法和技術，通過對監測數據深度挖掘分析，實現對瓦斯濃度精準預測，提高煤礦瓦斯災害預警能力，降低礦井瓦斯災害造成的經濟損失，保護人們生命安全。

為實現瓦斯濃度預測，國內外學者開展研究：文獻[3-6] 提出基于相空間重構理論、自適應混沌粒子群優化理論與支持向量機(SVM)相結合的瓦斯濃度預測方法；郭思雯等[7]提出基于自回歸集成移動平均模型的瓦斯濃度預測方法；武艷蒙等[8]利用SVM和差分進化(DE)算法建立預測模型，并基于馬爾可夫鏈的殘差修正預測瓦斯濃度變化趨勢；吳海波等[9]提出基于Spark Streaming框架的流回歸瓦斯濃度預測方法；Marek等[10-11]將ARIMA模型、K-臨近和模型樹法相結合，對瓦斯濃度進行預測，并且提出局部線性與差分整合移動平均自回歸模型組合的瓦斯濃度預測方法。上述研究方法均集中于單特征學習且數據集相對較小，因瓦斯濃度數據具有動態和非線性，使得上述方法在精確度和適用性方面表現不佳。

伴隨云計算和人工智能發展，門控循環單元(Gated Recurrent Unit，GRU)在智能裝備制造[12]、圖像識別[13-14]、能源預測[15-16]和智能交通[17]等方面得到廣泛應用。GRU是傳統循環神經網絡的優秀變體，其最大特點是善于處理復雜的多維時間序列。鑒于此，本文引入卷積神經網絡(CNN)，提取瓦斯數據時空特征，構建集時間與空間為一體的多維特征矩陣，將提取的數據信息輸入GRU，深度挖掘每個變量間的相互內在關系，并構建基于CNN-GRU的瓦斯濃度預測模型，研究結果在提高瓦斯濃度預測精度同時保證預測時效性。

1 門控循環單元(GRU)

傳統神經網絡層與層之間無節點連接，在解決時間序列問題上效果較差[18]。循環神經網絡與GRU結構原理如圖1所示，循環神經網絡(RNN)是1種具有反饋結構的網絡，在計算當下輸出時，隱藏層神經元會將儲存單元信息作為部分輸入，使輸出受先前輸出影響。因RNN善于處理時間序列信息，被廣泛用于具有時間信息數據挖掘工作。

圖1 循環神經網絡與GRU結構原理Fig.1 Recurrent neural network and GRU structure principle

長短期記憶(LSTM)是循環神經網絡的優秀變體，主要由輸入門、遺忘門和輸出門組成，輸入門控制細胞狀態，將信息選擇性保留下來，遺忘門將細胞狀態中的信息選擇性遺忘，輸出門針對隱藏層儲存單元決定輸出信息。同時，在整個過程中通過消除或增強輸入神經細胞單元信息控制細胞狀態[19]。

門控循環單元(GRU)將LSTM進一步改進[20]，結構如圖1(d)所示，通過將遺忘門和輸入門合并成更新門，改進LSTM的3門設計，目的是減少參數以優化細胞結構，提高運行效率，使得在訓練過程中更容易收斂。GRU主要按更新數據信息、數據信息匯總、重置數據信息和數據信息輸出4個步驟運行[21]。

1)更新數據信息。更新門控制隱藏層中的記憶信息，將信息進行線性變換，如式(1)所示：

zt=σ(Wz·[ht-1,xt])=σ(Whz·ht-1+Wxz·xt)

(1)

式中：zt為更新門信息；σ為sigmoid函數；t，t-1表示時刻；Wz為當前更新門權重；Whz表示在當前隱藏層狀態下更新門權重；Wxz為當前更新門輸入信息權重；ht-1為t-1時刻隱藏層狀態；xt為t時刻輸入信息。

2)數據信息匯總。確定前一時刻和當前時刻信息在隱藏層中遺忘的信息，如式(2)所示：

rt=σ(Wr·[ht-1,xt])=σ(Whr·ht-1+Wxr·xt)

(2)

式中：rt為重置門信息；Wr表示當前重置門權重；Whr表示在當前隱藏層狀態下重置門權重；Wxr表示當前重置門輸入信息權重。

3)重置數據信息。控制當前信息利用度和產生新記憶信息的數據量，作為輸入繼續向前傳遞，如式(3)所示：

(3)

式中：W表示權重；ut表示重置信息；tanh為雙正切函數變換；Wh表示當前隱藏層權重；Wx表示輸入信息權重；符號*表示線性變換。

4)數據信息輸出。利用更新門計算當前輸入信息，如式(4)所示：

ht=zt*ht-1+(1-zt)*ut

(4)

式中：ht表示t時刻隱藏層狀態。

2 瓦斯濃度預測模型構建

2.1 CNN-GRU預測模型

CNN-GRU預測模型結構如圖2所示，主要由輸入層、CNN層、全連接層、GRU層和輸出層5部分構成。輸入層是將某一時刻影響瓦斯濃度因素與瓦斯濃度數據本身串聯成1個向量，利用滑動窗口形成新的時間序列數據；CNN層是對輸入序列數據進行特征提取，CNN單元能夠通過卷積核運算自動提取數據局部變化趨勢，線性合并多組數據的抽象時空特性，提取多維時間序列特征；全連接層是將經多次核卷積后形成的抽象特征進行匯總，將卷積層輸出的多維特征矩陣轉化成一維向量，最后把轉換后的一維向量完整的傳遞給GRU網絡；GRU層主要是對CNN層提取的特征向量進行充分學習，記憶長期依賴的歷史數據，最終得到其內部特征變化規律，以此對未來瓦斯濃度數據進行預測；輸出層是將預測值反歸一化后輸出。

圖2 CNN-GRU組合模型結構Fig.2 Structure of CNN-GRU combined model

2.2 CNN參數設置

考慮瓦斯濃度數據的復雜性和CNN提取能力，將2D-CNN(二維卷積)作為網絡結構，以保證預測效果的穩定性。CNN特征識別功能有利于在不同層次的高維時間序列數據中自動提取共同特征，將數據轉換為沿時間軸的網格，利用CNN進行時間序列數據處理，如圖2所示。將最近L個日期的瓦斯濃度和具有N維屬性影響因素數據轉換成網格，在輸入層后僅連接2層卷積層，并采用Dropout技術防止過擬合，如圖2所示，目的是避免數據在通過池化層時丟失重要特征，以較少的層數快速提取高維特征。在連續卷積和池化后，通過Flatten層將數據降維，最后設置神經元數量分別為128，64，32的3層全連接層。CNN主要參數見表1。

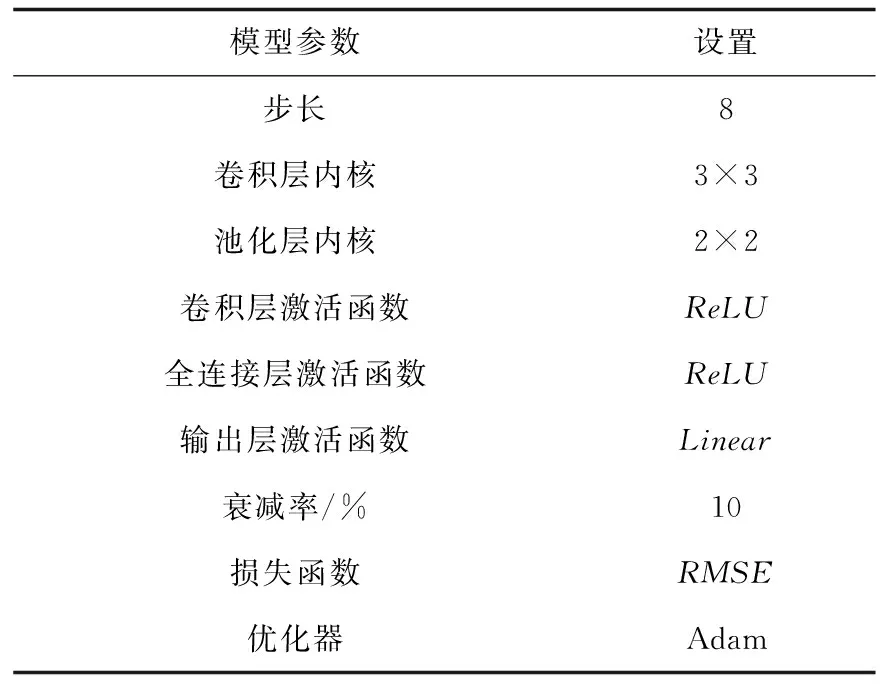
表1 CNN參數設置Table 1 Parameters setting of CNN

2.3 GRU參數設置

采用多對一和一對一2種回歸形式的2層GRU結構，使模型在最后1個時間步長前,對輸入的時間序列均能產生新的記憶狀態。由圖2可知，基于GRU的模型結構，其實現方法包括以下3個步驟:1)將數據以一對一的模式輸入到第1層GRU，并且每個時間步長的記憶狀態已經更新；2)第1層GRU的輸出以多對一的模式進入第2層GRU；3) 在第2層GRU輸出后進入全連接層。疊加2個層是為了預測每個時間步長，初步預測序列中趨勢，以幫助模型學習更高水平的時域特征表達。同理，建立3層全連接層，神經元數量分別設置為128、64、32，具體參數設置見表2。

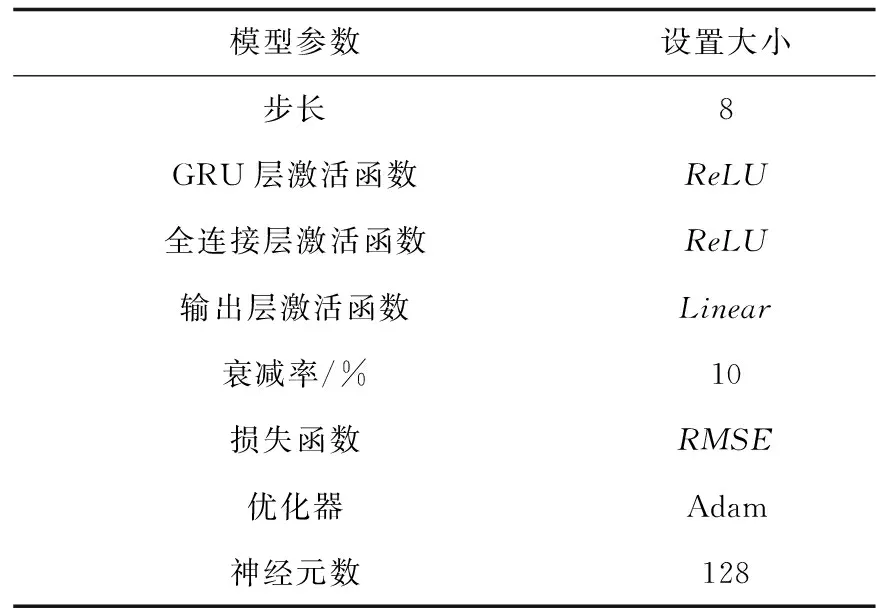
表2 GRU參數設置Table 2 Parameters setting of GRU

3 實例應用

3.1 數據來源與預處理

本文數據來自玉華煤礦2021年3月11日至2021年3月21日2407工作面每5 min的日常生產監測數據，包括瓦斯濃度、溫度、流量、負壓4個變量，共3 041組，數據特征如圖3所示。將數據按7∶3比例劃分為訓練集和測試集，用近似平均值補充缺失數據，刪除異常數據。為便于計算并提高預測精度，采用MinMaxScaler方法規范化，將數據縮放到[0,1]，如式(5)～(6)所示：

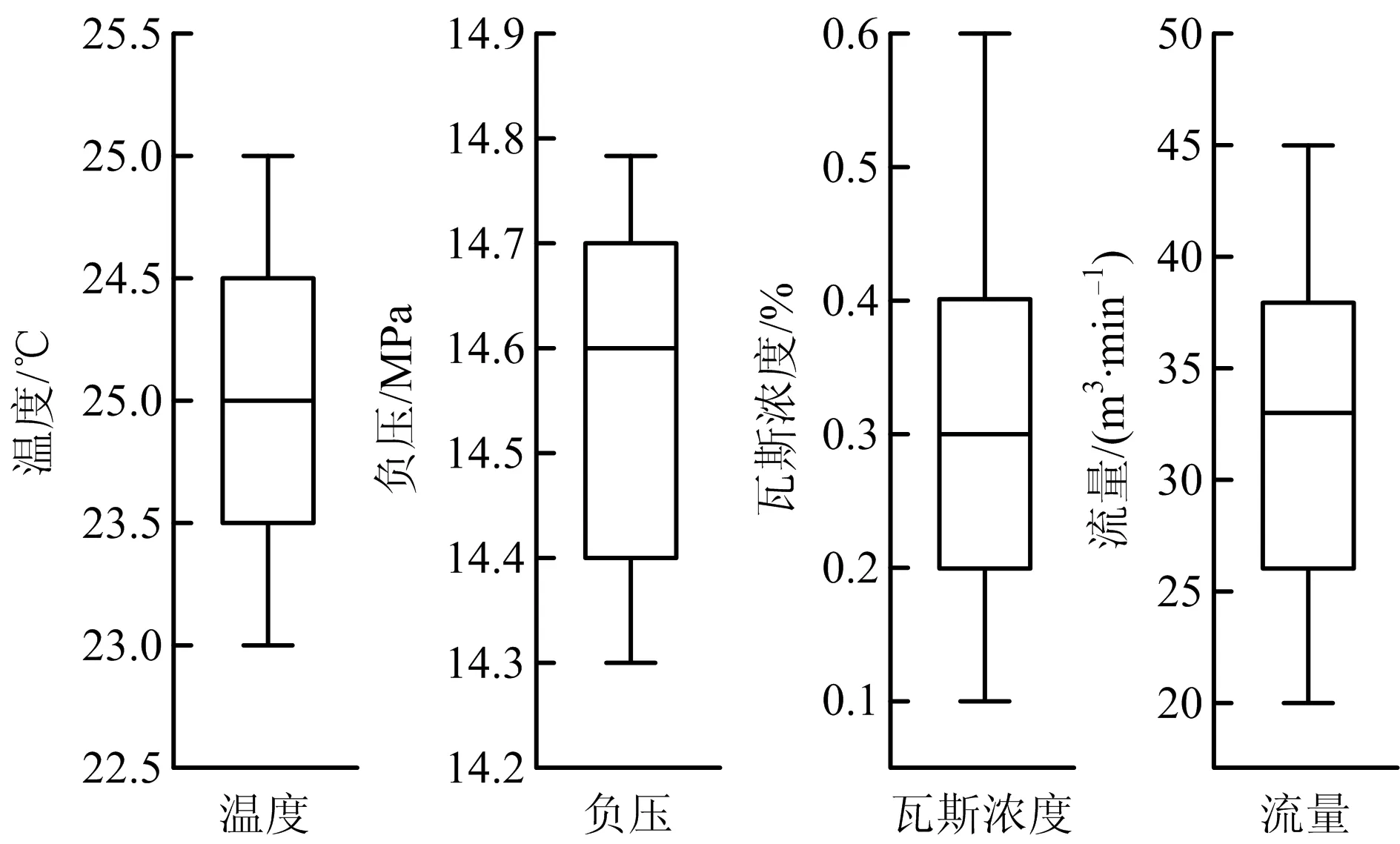
圖3 原始數據箱體圖Fig.3 Diagram of original data box

(5)

Xscaled=Xstd×(Max-Min)+Min

(6)

式中：Xstd表示放縮標準；X為數據；XMax，XMin表示數據最大值和最小值；Max，Min為數據縮放后的最大值和最小值；Xscaled表示最終放縮結果。處理后數據如圖4所示。

圖4 處理后數據Fig.4 Processed data

皮爾遜分析是衡量不同變量之間相關程度，其運行原理如式(7)所示[22]：

(7)

本文運用SPSS軟件對采集的4個變量進行皮爾遜相關性分析，結果見表3。由表3可知，溫度與瓦斯濃度呈高度相關，流量和負壓與瓦斯濃度呈中度相關。因此，本文選擇瓦斯濃度、流量、溫度和負壓4個變量作為預測模型的輸入是合理的。

表3 各影響因素相關性分析結果Table 3 Correlation analysis results of each influencing factor

本文實驗采用Python3.7開發語言、Pycharm社區版集成環境，GRU模型和CNN模型均來自Keras2.1.5，計算機配置為CPU(i7-8550),顯卡RX550，內存8GB。通過2個評價指標衡量模型預測精度。

平均絕對誤差(MAE)如式(8)所示：

(8)

均方根誤差(RMSE)如式(9)所示：

(9)

式中：fi，yi分別為預測值和真實值；m為樣本個數。

3.2 模型運行效率對比

為比較不同模型達到最優結果時的運行效率，將CNN-GRU組合模型與傳統機器學習模型LSTM和GRU進行比較，采用訓練集導入模型，在訓練過程中，當損失函數值連續增加或無明顯減少時，提前終止訓練，經過3次訓練后結果如圖5～6所示，LSTM、GRU和CNN-GRU的平均訓練輪次(Epoch)分別為325，200，159次；LSTM、GRU和CNN-GRU的平均訓練時間分別為590，371，241 s；CNN-GRU的運行效率比LSTM和GRU分別提高59.15%，35.04%，并且CNN-GRU模型需要的訓練輪次最少，較大幅度降低內存消耗。

圖5 3種模型訓練時間和訓練輪次比較Fig.5 Comparison on training time and training round of three models

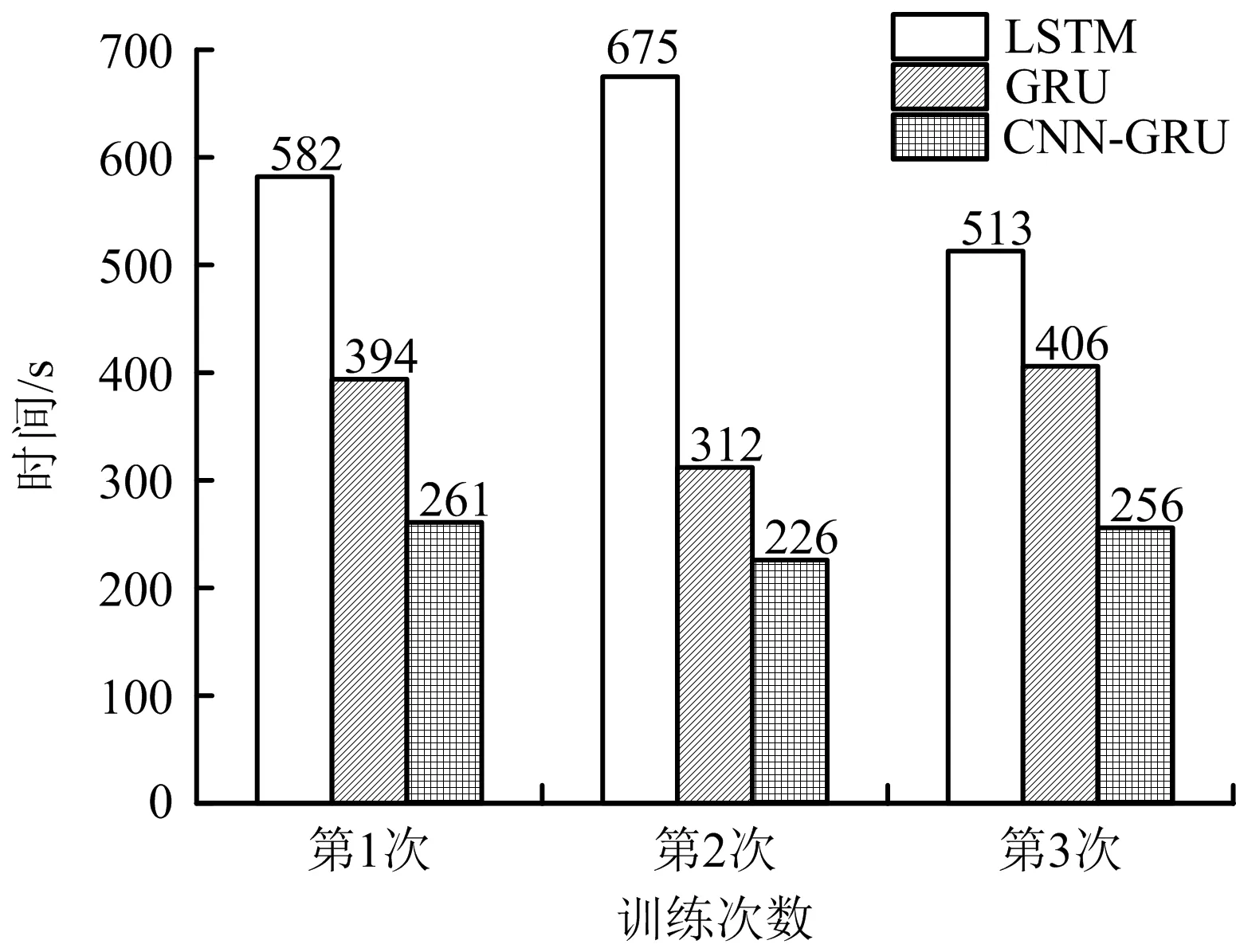
圖6 3種模型訓練時間比較Fig.6 Comparison on training time of three models

3.3 模型精度對比

LSTM、GRU和CNN-GRU 3種模型測試誤差結果如圖7所示，CNN-GRU測試過程中平均絕對誤差和均方根誤差均優于LSTM和GRU，同時CNN-GRU的平均絕對誤差誤差主要集中在0.045～0.052，均方根誤差主要集中在0.007～0.01，誤差波動范圍更小，具有較高的穩定性。

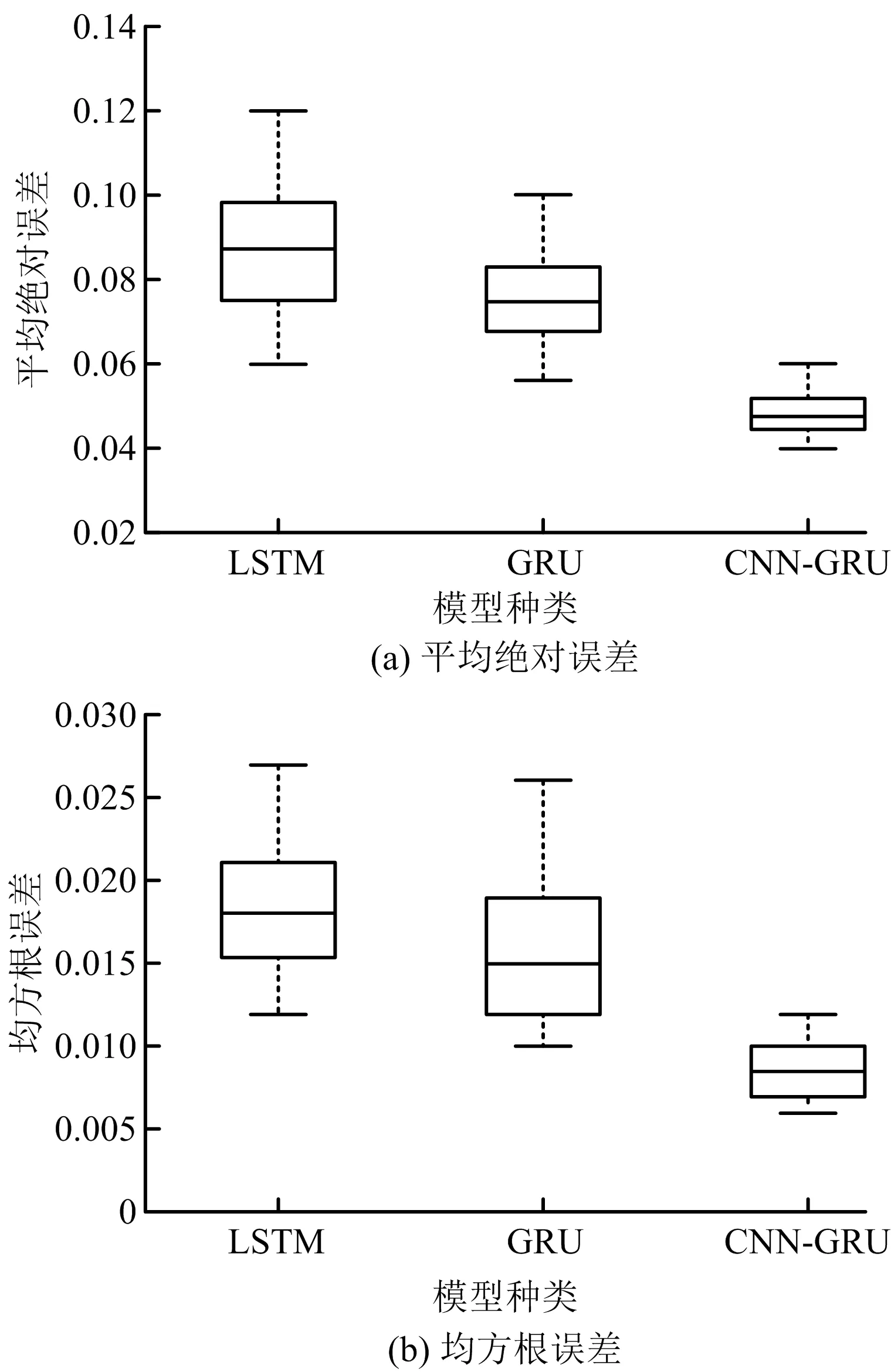
圖7 3種模型預測結果誤差對比箱線Fig.7 Box line for comparison on error of prediction results by three models

LSTM、GRU和CNN-GRU的整體預測結果如圖8～10所示，CNN-GRU可有效預測瓦斯時間序列的峰谷值，在整體預測趨勢上優于LSTM和GRU。3種模型詳細誤差對比見表4，CNN-GRU的平均絕對誤差和均方根誤差相對最低，分別可降至0.042和0.006，平均誤差分別為0.047和0.008，相比于LSTM降低46.6%，55.6%，相比于GRU降低37.3%，50.2%。

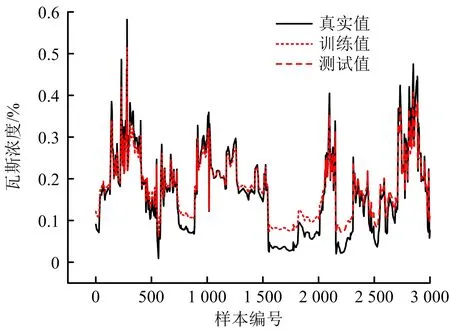
圖8 LSTM模型預測效果Fig.8 Prediction effect of LSTM model

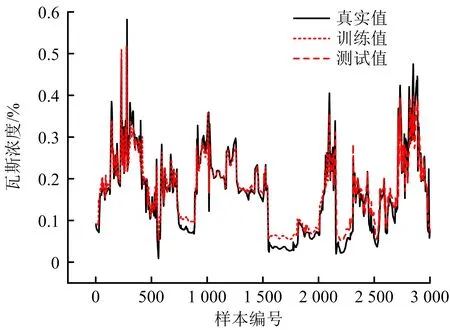
圖9 GRU模型預測效果Fig.9 Prediction effect of GRU model

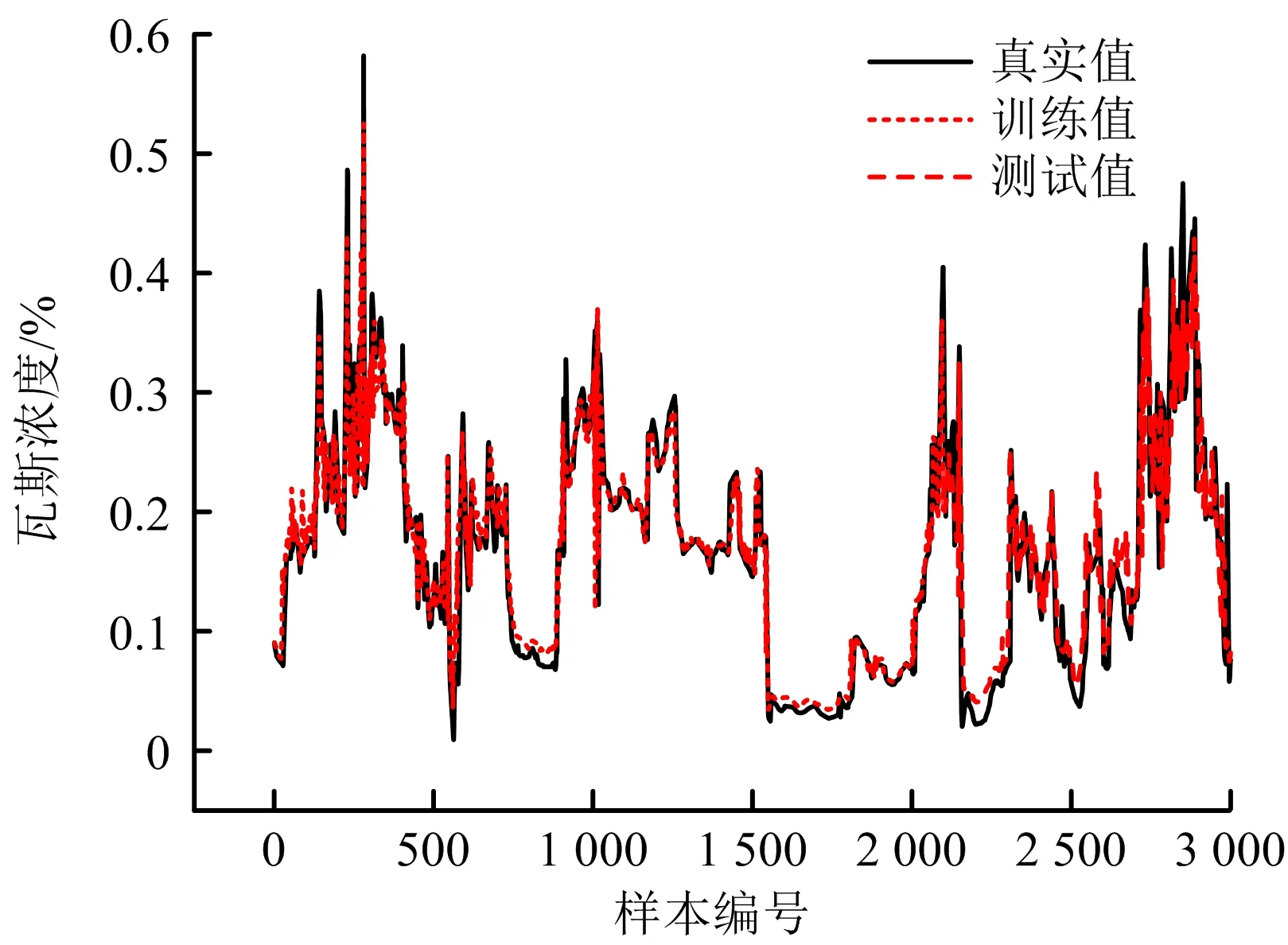
圖10 CNN-GRU組合模型預測效果Fig.10 Prediction effect of CNN-GRU model

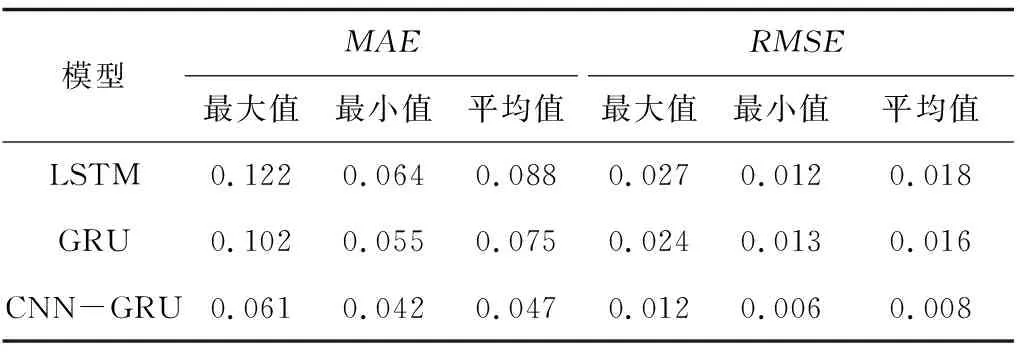
表4 3種模型預測結果誤差Table 4 Prediction results error of three models

4 結論

1)基于CNN-GRU的瓦斯濃度組合預測模型，能夠克服傳統預測方法的數據特征單一和解決非線性能力差的問題，利用多類型數據對瓦斯濃度進行時序性預測。

2)采用MinMaxScaler和皮爾遜相關性分析對實驗數據進行預處理和相關性分析，提高數據質量同時，證明多種影響因素作為模型輸入的合理性。

3)CNN-GRU組合模型相比于LSTM、GRU模型有更高的預測精度，平均絕對誤差和均方根誤差可降至0.042和0.006，更適用于瓦斯濃度時間序列預測，并且在訓練過程中所需訓練輪次和運行時間相對較少，降低內存消耗，提高預測效率，具有更高的應用價值。