基于運動性能分析的仿人機械臂尺度優化

孫 鵬 李研彪 張 聰 單曉杭 岳 義 韋寶琛

1.浙江工業大學機械工程學院，杭州，3100232.上海工程技術大學機械與汽車工程學院，上海，201620

0 引言

目前，多關節串聯機械臂的研究熱點聚焦于軌跡規劃[1-2]和柔順控制[3-4]等方面，這拓展了多關節串聯機械臂在人機共融領域的應用，但仍受到串聯機構固有特性的限制。并聯機構雖然有效地彌補了這種缺陷，但也存在工作空間小和運動耦合等缺點[5]。而將串聯、并聯機構組合而成的混聯機構作為結構本體，則巧妙地結合二者的優點[6-7]，通過合理布局可獲得良好的運動性能。因此，混聯機構的構型合成[8-9]和性能優化[10-11]引起了研究人員的極大興趣。

綜合來講，串并混聯機構主要有三種類型：并聯-串聯[12-13]、串聯-并聯[14-15]、并聯-串聯-并聯[16-17]。并聯-串聯構型的混聯機構主要應用于機床領域，其中以五自由度混聯機床的應用最為成熟。并聯機構可為末端執行器提供較大負載，并且一定程度上滿足工作空間的需求。串聯-并聯構型的混聯機構主要應用于外科手術和大曲面拋光領域，串聯機構能夠提供足夠大的工作空間并且運動靈活性高，末端的并聯機構則具有精細的姿態調整功能，更適用于要求精細化操作的外科手術領域和連續曲率變化的曲面拋光領域。并聯-串聯-并聯構型兼顧了上述兩種構型的優點，既滿足了末端執行位置和姿態空間的要求，也能提高機構整體的負載慣性比。這類構型的機構功能劃分與人體手臂相類似，可被應用于仿人機械臂領域[6]，但它存在工作空間復雜以及性能指標定義不清晰等不足。

尺度優化是機構學理論的一個重要課題，它主要涉及兩個關鍵問題：優化目標函數的確定和優化方法的選擇。對于優化目標，串聯機構主要根據雅可比矩陣條件數等[18]進行優化；并聯機構主要考慮輸入與輸出的運動/力的傳遞效率[19]；混聯機構的性能優化要綜合考慮末端執行器的運動特點，分別建立相應傳遞性能指標。優化設計方法主要分為兩類，一種是應用智能算法[20-22]，另一種是構造參數的尺寸空間[23]。智能算法主要解決具有實時性要求的優化問題，只能給出解集，不能反映參數與指標之間的復雜關系，并且初值選取與參數設置對智能算法的收斂性和運行效果產生較大影響。尺寸空間是最早被采用的設計方法，該方法兼顧各項指標又能保證各項指標之間的相互獨立，但它不適合處理多目標和多參數的設計。因此，設計一種三維可視化的尺寸空間，直接展示性能指標與結構參數間的映射關系是一項具有意義的研究。

本文基于上述分析，根據仿人機械臂的運動特性，分離設定了各關節的性能指標，提出了一種多參數平面模型技術，實現了三維可視化優化設計。在此基礎上，完成了仿人機械臂的結構參數優化工作，并確定了相應的關節姿態空間與指標分布情況。

1 仿人機械臂描述

1.1 構型布局

仿人機械臂的三維模型和機構原理圖見圖1，肩關節以2個轉動自由度的球面5R并聯機構為原型，其兩條運動鏈分別由轉動副A1、B1、C1與A2、C2構成。肘關節為三自由度的RRR串聯機構，由轉動副D、E、F組成。腕關節采用3個轉動自由度的對稱型球面3-RRP并聯機構，其3條運動鏈分別由轉動副Hj、Kj和移動副Pj構成(j=1，2，3)。靜坐標系OXYZ以點O為中心，點O為肩關節的轉動中心，軸Y與軸OA2重合；坐標系OX1Y1Z1是肩關節的動參考系，軸X1與軸OC2重合，軸Z1與軸OC1重合；坐標系O2X2Y2Z2是肘關節的動參考系，點O2為轉動副的軸線交點，軸Z2與軸O2D重合；坐標系O3X3Y3Z3是腕關節的定參考系，O3為轉動副軸線與移動副法線的公共交點，軸Z3與軸O2F重合。坐標系O4X4Y4Z4為末端動參考系(點O4與O3重合)。初始位姿時，各動坐標系的軸線與靜坐標系的軸線平行。

(a)三維模型

針對各關節的構型布局，定義相關結構參數，并根據結構緊湊性與協調性的設計經驗設定各個參數的取值范圍，如表1所示。

表1 仿人機械臂的結構參數

1.2 運動特性簡述

在以往的工作中，該仿人機械臂的運動學求解方法已經被提出[6]，為性能指標的設定提供了基礎。基于旋量理論與指數積公式，該仿人機械臂的相關運動學解析式為

(1)

(2)

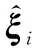
通過分析式(1)和式(2)可得，肩關節和肘關節(不包含轉動副F)確定了末端平臺參考點O4的位置空間，并為末端平臺提供了寄生姿態。驅動副F和腕關節決定了末端平臺的主動姿態空間。

2 性能指標設定

針對仿人機械臂各關節的主要功能，分別對肩關節、肘關節、腕關節的運動學性能進行分析。其中，基于能效系數建立從屬于并聯機構的肩關節與腕關節的傳遞/約束指標；基于雅可比矩陣的條件數建立肘關節的線速度性能指標。

2.1 能效系數

對于并聯機構，根據旋量理論，力旋量與運動旋量的互易積表示力旋量對按此運動旋量進行運動的剛體所做功的瞬時功率，并且其最大值作為視在功率。將實際功率與視在功率的比值作為能效系數，能效系數越大，表示能量傳遞效率越好。因此，可得輸入與輸出的傳遞能效系數[19]為

(3)

(4)

式中，ξT為傳遞力旋量；ξI為輸入運動旋量；ξO為輸出運動旋量；λI為輸入傳遞能效系數；λO為輸出傳遞能效系數。

輸入與輸出的約束能效系數[19]為

(5)

(6)

式中，ξC為約束力旋量；ξR為受限運動旋量；ΔξO為輸出受限運動旋量；кI為輸入約束能效系數；кO為輸出約束能效系數。

一般情況下，上述4組能效系數的最小值為該并聯機構的整體性能指標：

Υ=min(λI，λO，κI，κO)

(7)

2.2 肩關節的性能指標

(8)

式中，c、s分別為cos、sin的縮寫。

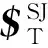
(9)

(a，b，c)=(RSJSB1)×(RSJSC1)

式中，SB1為初始位姿下轉動副B1的軸線矢量坐標；SC1為初始位姿下轉動副C1的軸線矢量坐標；RSJ為肩關節的姿態轉換矩陣(Z-Y-X型歐拉角描述)。

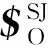
(10)

(cβ1，0，-sβ1)=RSC2

(d，e，f)=(sβ1，0，cβ1)×(a，b，c)

式中，SC2為初始位姿下轉動副C2的軸線矢量坐標。

(11)

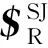
(12)

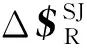
(13)

(c，0，-a)=(0，1，0)×(a，b，c)

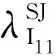
(14)

2.3 腕關節的性能指標

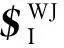
(15)

其中，每個輸入運動旋量的前三維坐標為該輸入轉動副的軸線矢量坐標SH1、SH2、SH3。

(16)

(a1，b1，c1)=(RWJSK1)×(RWJSP1)

(a2，b2，c2)=(RWJSK2)×(RWJSP2)

(a3，b3，c3)=(RWJSK3)×(RWJSP3)

式中，SK1為初始位姿下轉動副K1的軸線矢量坐標；SP1為初始位姿下移動副P1圓弧軌跡的軸線矢量坐標；SK2為初始位姿下轉動副K2的軸線矢量坐標；SP2為初始位姿下移動副P2圓弧軌跡的軸線矢量坐標；SK3為初始位姿下轉動副K3的軸線矢量坐標；SP3為初始位姿下移動副P3圓弧軌跡的軸線矢量坐標；RWJ為腕關節的姿態轉換矩陣(tilt-and-torsion angles描述)。

(17)

(d1，e1，f1)=(a2，b2，c2)×(a3，b3，c3)

(d2，e2，f2)=(a3，b3，c3)×(a1，b1，c1)

(d3，e3，f3)=(a1，b1，c1)×(a2，b2，c2)

(18)

(19)

(20)

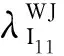
(21)

2.4 肘關節的性能指標

在物體坐標系(O4X4Y4Z4)中建立末端參考點的線速度雅可比矩陣：

(22)

采用雅可比矩陣條件數的倒數為性能指標，它為最小奇異值與最大奇異值之比，反映末端平臺的速度大小對關節速度的敏感度：

(23)

式中，Kv為線速度性能指標；σmin為最小奇異值；σmax為最大奇異值。

由式(22)可知，肩關節的等效轉角β1不影響矩陣4Jv取值；當cθγ1= cθD= 0 或sθE=0 時，矩陣4Jv的秩由3變為2，末端參考點失去沿物體坐標系Z4軸的線速度。

3 參數優化

結構參數優化對機構各運動關節的布局起到關鍵作用，對機器人的性能尤為重要。本文將指定工作空間下的性能指標均值作為全域性能指標，并根據各關節的性能分析，基于多參數平面模型，實現了各關節的結構參數優化。

3.1 多參數平面模型

針對多參數可視化優化設計，提出了一種多參數平面模型。多參數平面模型原理為參數的組合排序，具體做法如下：假設有l個參數，每個參數取k個采樣點，取任意兩個參數構成方形散點圖；方形的每個交點代表一個組合，這些交點被映射在一條對角線上；這些對角線也按照上述方法形成一個新的正方形(或長方形)散點圖，以獲得新的對角線。重復此步驟，直到得到最后一個正方形(或長方形)散點圖，其交點包含所有參數的組合。注意，長方形散點圖是由l為奇數引起的。以a、b、c、e4個參數為例展示模型，每個參數取相同數量的采樣點al、bl、cl、dl(l=1，2)，如圖2所示。

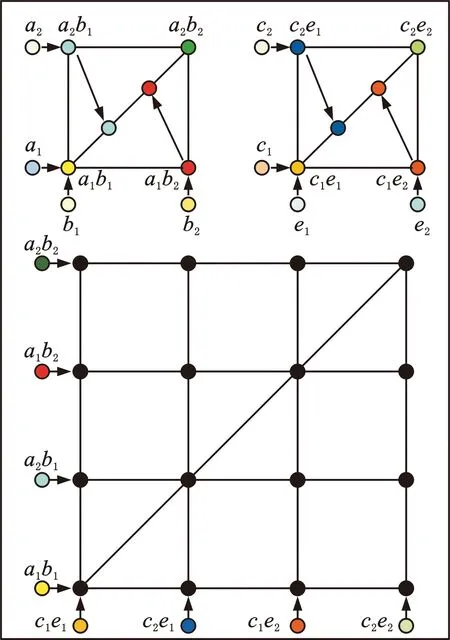
圖2 多參數平面模型Fig.2 Multi-parameter plane model

3.2 肩關節優化設計

設定肩關節的姿態搜索空間：β1∈[-160°， 40°]，γ1∈[-160°，40°]。肩關節的結構參數取值范圍如表1所示。基于多參數平面模型建立肩關節全域性能指標，如圖3所示。

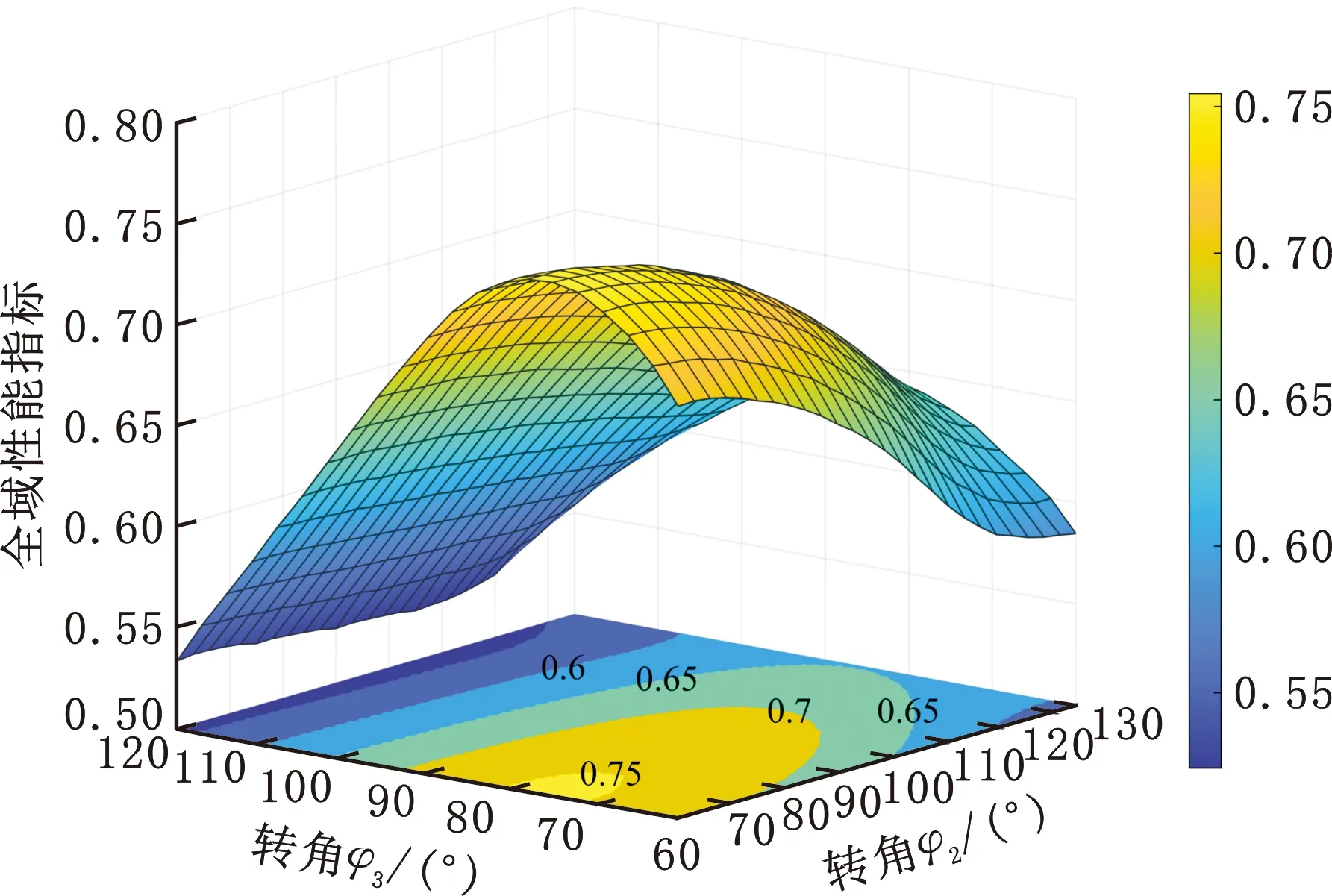
圖3 肩關節全域性能Fig.3 Global performance of shoulder joint

整體上看，全域性能指標隨φ2增大而減低；隨φ3增大呈現出先增大后減小的趨勢，并在φ3∈[70°， 80°]時取較大值；φ2與φ3差值較小時，指標值相對較高。為進一步分析參數對性能的影響，取9組[φ2,φ3]的參數組合：[60°，75°]、[90°，75°]、[120°，75°]、[60°，90°]、[90°，90°]、[120°，90°]、[60°，105°]、[90°，105°]、[120°，105°]，各組參數下的肩關節性能表現如圖4所示。

圖4中的空白部分表示肩關節的運動性能指標值小于0.5，當肩關節位姿處于此區域時傳遞與約束性能較差，并且此區域的對稱線為肩關節的奇異位姿。由圖4可知，φ2的取值影響肩關節奇異位姿在工作空間中的位置。在β1∈[-160°，40°]、γ1∈[-160°,40°]搜索空間范圍內，當β1=-φ2或β1-φ2= 180°時，肩關節奇異，這造成全域性能隨φ2值增大而降低。φ3的取值影響肩關節運動性能于奇異位姿附近的取值，當φ3>75°時，運動性能指標值小于0.5的范圍隨φ3值增大而擴展，從而造成全域性能降低。上述分析符合圖3表現出的全域性能變化趨勢。

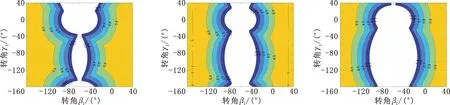
(a)φ2 = 60°，φ3= 75° (b)φ2 = 60°，φ3= 90° (c)φ2 = 60°，φ3= 105°

3.3 腕關節優化設計

采用tilt-and-torsion angles方法描述腕關節的全姿態空間，并設定搜索范圍：φ∈[-180°，180°]，θ∈[0°，90°]，ψ∈[-180°，180°]。腕關節的結構參數取值范圍如表1所示，參數φ6、φ7與φ8分別取25、7與13個采樣點，則共有2275種參數組合，建立平面模型如圖5所示。基于多參數平面模型建立腕關節全域性能指標，如圖6所示。在全姿態搜索空間下，腕關節的姿態空間大小也對其全域性能取值產生影響，因此圖7以搜索點數目展示了不同參數組合下的腕關節姿態空間。

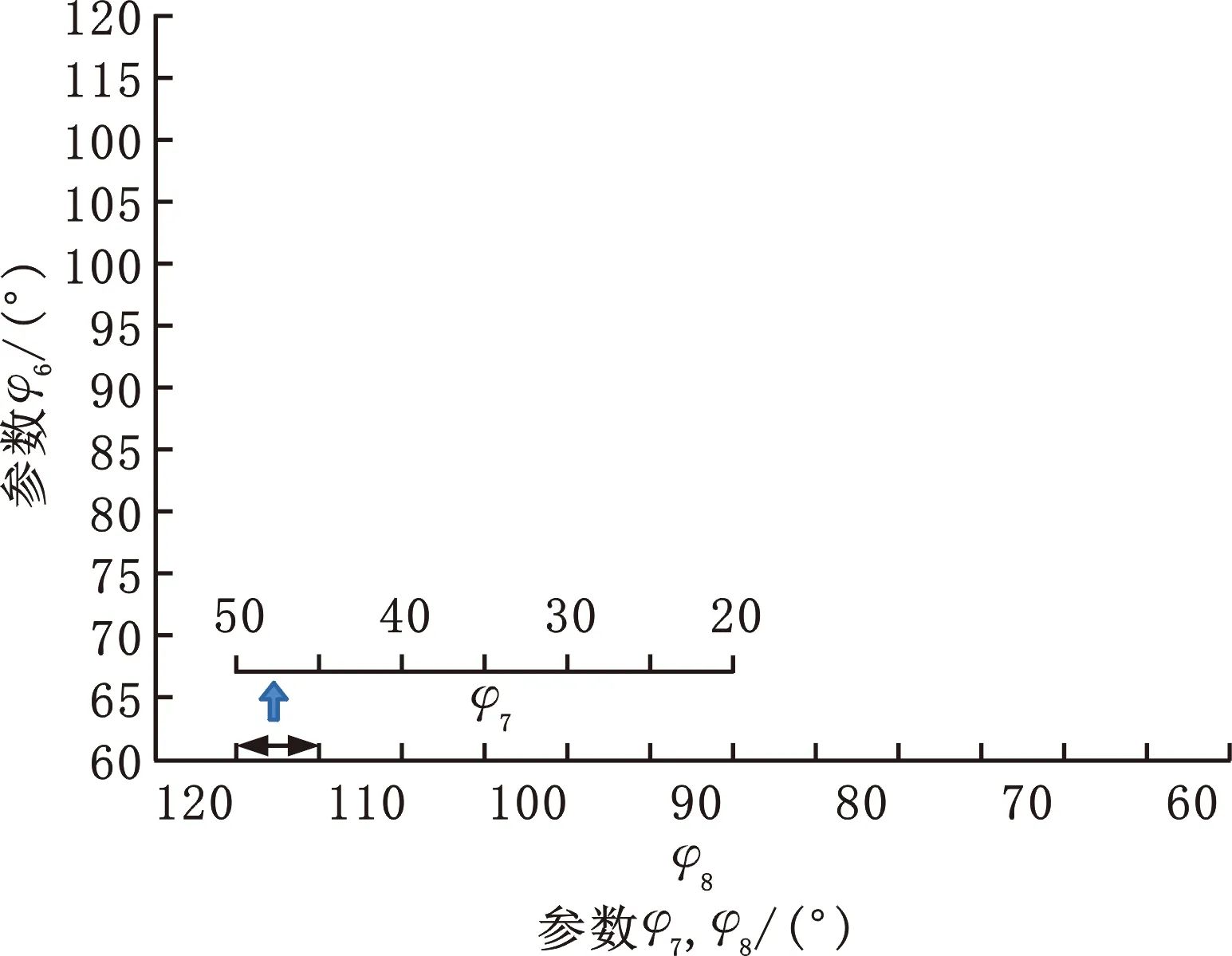
圖5 腕關節全域性能參數φ6、φ7與φ8組合的平面模型Fig.5 Plane model for parameter combinations of φ6，φ7 and φ8

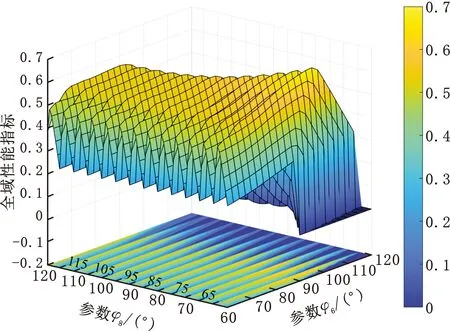
圖6 腕關節全域性能Fig.6 Global performance of wrist joint

圖7 腕關節姿態空間Fig.7 Orientation space of wrist joint

由圖6可知：全域性能指標隨φ6增大而緩慢增大，在φ6= 90°時取最大值，而之后迅速減小；隨φ7增大而急劇增大；隨φ8增大呈現出緩慢降低的趨勢。由圖7可知，姿態空間隨φ6增加先增大而后減小，隨φ8增大呈現出明顯增加的趨勢。為進一步明確參數對性能的影響，取3組參數組合分析。當[φ6，φ7，φ8]取值[100°，50°，60°]，腕關節全域性能最高時，姿態空間很小，如圖8a所示(其中T&T轉角表示tile-and-torsion angles)。這表示當φ8取值較小時，降低了腕關節姿態空間的可達范圍，使得全域性能相對較高。當[φ6，φ7，φ8]取值[110°，50°，120°]，腕關節姿態空間較大，全域性能較差，如圖8b所示。這表示當φ6> 90°時，盡管腕關節姿態空間會有明顯的增大，但每個位姿點的性能變差，造成全域性能降低。當[φ6，φ7，φ8]取值[90°，50°，120°]，腕關節姿態空間滿足|φ+ψ| ≤ 30°與θ∈[0°，30°]時，其性能大于0.7，如圖8c所示。

(a)φ6 = 100°，φ7 = 50°，φ8 = 60°

3.4 肘關節優化設計

根據3.2節分析的仿人肩關節優質姿態空間，并考慮仿人肘關節的工作空間區域相對于人體肘關節活動區域的實現程度，設定搜索空間：γ1∈[-150°，30°]，θD∈[-90°，30°]，θE∈[-120， 0°]。肘關節的結構參數取值范圍如表1所示。基于多參數平面模型，建立肘關節全域性能指標，如圖9所示。

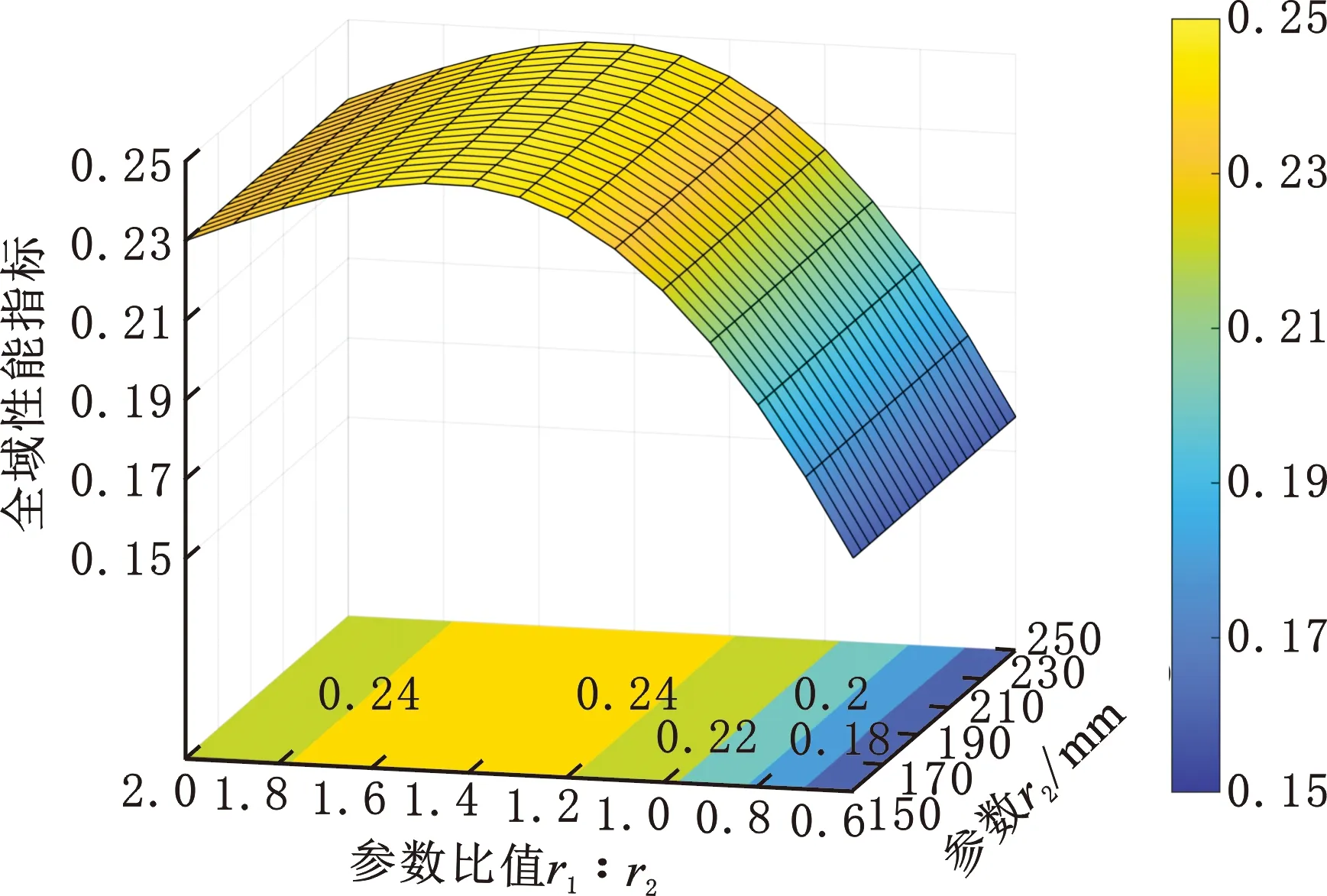
圖9 肘關節全域性能Fig.9 Global performance of elbow joint

由式(22)和圖9可知，盡管r2會影響矩陣4Jv的取值，但不會改變矩陣4Jv的條件數。并且，全域性能指標只與r1和r2的比值有關，隨r1和r2的比值增加而先增大后減小，在r1∶r2= 1.5時取最大值。搜索空間的轉角參數γ1、θD與θE分別取19、9與9個采樣點，則共有1539種參數組合，建立平面模型如圖10所示。取r1∶r2= 1.5，得到條件數在搜索空間的分布情況，如圖11所示。

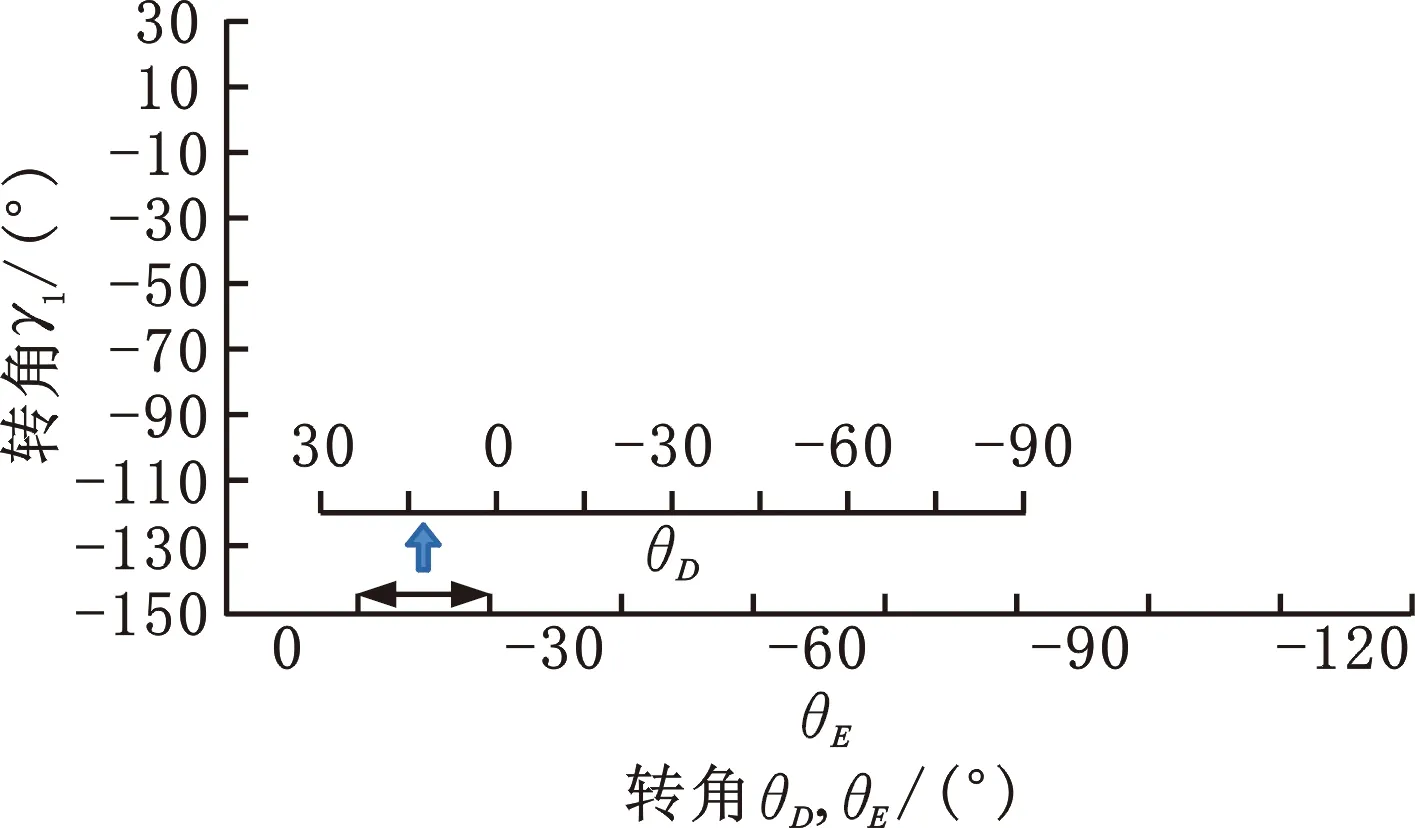
圖10 肘關節性能分布轉角γ1、θD與θE組合的平面模型Fig.10 Plane model for angle combinations of γ1，θD and θE

由式(22)和圖11可知，當θE=0°時，仿人機械臂的大臂OO2與小臂O2O3共線，末端參考點處于此方向的極限位置，失去了沿該方向的線速度，從而不存在奇異值，導致線速度雅可比矩陣的條件數為0。在θE∈[-120°，0°]搜索空間內，條件數隨|θE|的增大而變大。當γ1=θD= -90°時，仿人肩關節的等價關節Y1與轉動副D共線，末端參考點失去了沿小臂O2O3方向的線速度，從而不存在奇異值，導致線速度雅可比矩陣的條件數為0。在γ1∈[-150°，30°]與θD∈[-90°，30°]搜索空間內，在γ1=θD= -90°附近的條件數取值較小；在剩余搜索范圍內，條件數主要由姿態角γ1決定；γ1= 0°時的條件數取值最大。

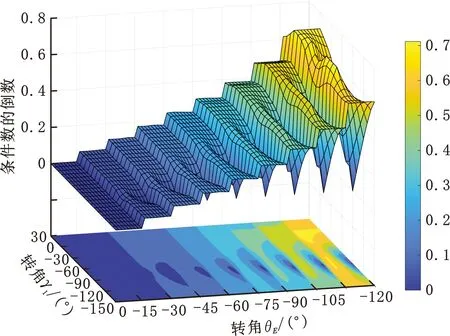
圖11 肘關節性能分布Fig.11 Performance distribution ofelbow joint

綜上分析，選取φ2=120°、φ3=90°、φ6= 90°、φ7= 50°、φ8=120°。參照人體手臂的總長度，選取r1= 290 mm、r2= 193 mm。考慮仿人關節的姿態空間區域相對于人體關節活動區域的實現程度，確定優質姿態空間為β1∈[-110°，40°]、γ1∈[-150，-120°]∩[-60°，30°]、θD∈[-45°，30°]、θE∈[-120°-60°]，|φ+，ψ|≤30°、θ∈[0°，30°]。在此基礎上，肩關節全域性能指標為0.78；腕關節全域性能指標為0.67；肘關節全域性能指標為0.42，全域條件數為2.38。

4 結論

(1)球面并聯機構具有良好的約束性能，各條運動支鏈的旋量系均為線矢量或純力偶，基于公共約束力旋量的輸入與輸出約束能效系數均恒為1。

(2)基于仿人機械臂的運動特性，分別設定了各關節的性能指標。通過分離整體運動性能，規避了分析多關節機構所面臨的性能耦合問題，進一步明晰了串并混聯機構的構型優勢。肩關節作為仿人機械臂的基部，全域性能指標為0.78，提供了良好的傳遞約束性能；肘關節作為仿人機械臂的主體，全域條件數為2.38，具有較低的誤差敏感度，有效地實現了運動傳遞功能；腕關節作為仿人機械臂的末端，具有恒為1的約束性能，滿足末端姿態調整要求。

(3)提出了多參數平面模型，有效地解決了多參數優化的可視化問題。對于肩關節，當β1=-φ2或β1-φ2= 180°時處于奇異位姿；對于肘關節，r1和r2的比值是影響線速度雅可比矩陣條件數的主要因素，并且當θE= 0°或γ1=θD= -90°時末端參考點處于極限位置；對于腕關節，需考慮姿態空間大小對全域性的影響。