基于最大重加權峭度盲解卷積的風電故障診斷

吳 磊 王家序 張 新 劉治汶

1.西南交通大學機械工程學院，成都，6100312.電子科技大學自動化工程學院，成都，611731

0 引言

風電機組長期在陣風等復雜交變載荷作用下工作，惡劣工況以及復雜機械結構嚴重影響機組運行安全與維護保障[1-2]。風電機組關鍵部件——齒輪和軸承容易出現各種形式的故障，一旦出現故障可能造成巨大損失，因此研究風電機組的運行狀態監測與故障診斷具有重要意義[3-6]。

得益于振動信號中含有豐富的機械運行狀態信息，振動監測成為旋轉機械狀態監測與故障診斷的有效技術[7-9]。然而，測量信號中由齒輪或軸承局部缺陷所引起的故障沖擊序列經常被環境噪聲以及其他干擾成分所掩蓋，加上傳遞路徑的傳播效應，導致齒輪和軸承的故障診斷存在較大困難[10-12]。盲解卷積方法通過設計一個有限長脈沖響應(finite impulse response，FIR)濾波器，能實現在未知振動源、傳輸通道特性以及噪聲強度的情況下從測量信號中恢復故障沖擊特征，在旋轉機械故障診斷領域引起了廣泛的關注[13]。在設計FIR濾波器時，通常是基于信號的某種數字特征，且待恢復的信號成分與干擾成分在此特征上表現出可區分性[14-15]。如經典的MED(minimum entropy deconvolution)方法利用地震波與環境噪聲在峭度方面的不同，成功獲取地震相關信息[16]。MED具有調參少、收斂快等優勢，但用于旋轉機械振動信號分析時卻傾向于恢復單個主導沖擊而非故障沖擊序列，原因在于相同信號長度下單個沖擊的峭度遠大于沖擊序列的峭度。在機械故障診斷領域，MED仍得到了部分應用。ENDO等[17]結合MED與自回歸(auto-regressive，AR)，提出AR-MED濾波方法并用于齒輪剝落和齒角裂紋檢測；YANG等[18]利用MED對原始信號進行預處理，提取被強噪聲干擾的軸承特征信息；LIU等[19]利用MED凸顯故障沖擊特征，使得包絡分析更準確有效。然而，值得注意的是，在上述應用中，MED傾向于恢復單個沖擊的缺陷并未得到有效解決。

為克服MED這一缺陷，多種盲解卷積方法被提出并應用到機械故障診斷中，其中最常見的方法包括MCKD(maximum correlated kurtosis deconvolution)[20]、MOMEDA(multipoint optimal minimum entropy deconvolution adjusted)[21]以及CYCBD(maximum second-order cyclostationarity blind deconvolution)[22]。在恢復故障沖擊序列方面，這三種方法表現出優異的性能，但它們卻依賴于待恢復沖擊序列頻率這一先驗知識，即方法并非全“盲”。實際應用中，受速度波動等因素的影響，難以預先獲知準確的故障特征頻率，嚴重影響了三種方法的有效性，從而也限制了方法的適用性[23-25]。近年來，涌現出不少解卷積方法并被用于機械故障診斷中。DUAN等[26]提出利用形態濾波來提高MED的濾波效果；MA等[27]基于稀疏子空間重編碼提出了一種有效的齒輪箱故障診斷方法；ZHANG等[28]利用連續振動分離這一方法克服調制效應并結合MED提出了一種齒輪故障診斷方法；MIAO等[29]采用基尼系數作為盲解卷積指標，在旋轉機械故障診斷中表現出較好性能；LIANG等[30]提出的最大平均峭度解卷積方法對典型干擾具有較好的魯棒性，但不足之處在于所提方法的有效性仍依賴先驗故障特征頻率。

為有效恢復故障沖擊序列、準確診斷齒輪故障，本文提出了一種新的盲解卷積方法——最大重加權峭度盲解卷積方法。該方法利用重加權峭度對故障信號中單個或少量強沖擊干擾具有較好魯棒性，以及不依賴待恢復故障沖擊序列先驗知識的特性，能有效地解決基于峭度最大化方法傾向于恢復單個主導沖擊的問題。同時，相較于常見依賴故障特征頻率先驗知識的非全“盲”方法，所提方法在齒輪故障診斷方面具有更強的適用性。通過仿真信號分析以及風電機組故障診斷應用研究來驗證所提方法的有效性。

1 常見解卷積指標及其主要缺陷

1.1 問題描述

在旋轉機械故障診斷中，受多振動源以及復雜傳遞路徑和噪聲干擾等多因素的影響，振動信號中由齒輪局部缺陷所引起的故障沖擊成分往往被其他干擾所掩蓋。由傳感器測量得到的振動信號x一般可表示為

x=s0*gs+n*gn

(1)

式中，s0為局部缺陷產生的故障沖擊成分；n為干擾成分(如高斯噪聲、電流產生的強沖擊干擾等)；*表示卷積運算；gs、gn分別為故障沖擊成分與干擾成分的脈沖響應函數。

盲解卷積旨在設計一FIR濾波器h，從振動信號中恢復得到故障沖擊成分s0，其過程如圖1所示，可表述為

s=x*h=(s0*gs+n*gn)*h≈s0

(2)

其中，濾波信號s為s0的估計值。在此過程中，利用衡量指標(如峭度、相關峭度、D-范數等)來評估濾波信號以及作為目標函數求解濾波器是必要的，而不同的指標表現出不同的性能，甚至直接決定方法的有效性。

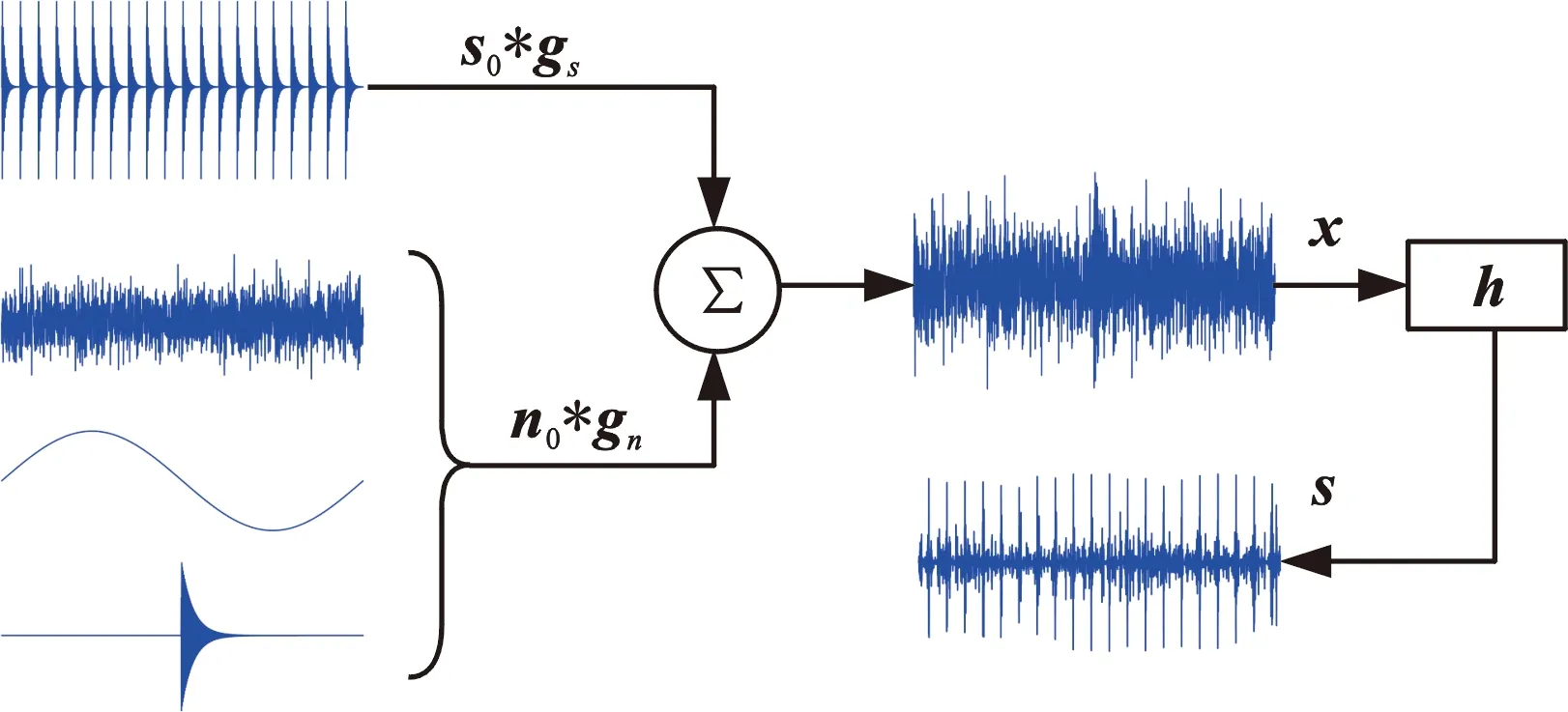
圖1 盲解卷積技術基本原理Fig.1 The basic principle of blind deconvolution techniques

1.2 峭度

在MED方法中，峭度被用作盲解卷積指標。盡管此方法名為“最小熵解卷積”，但它并非使濾波信號的熵最小，而是通過最大化濾波信號的峭度來求解濾波器h，即

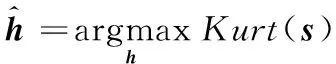
(3)

(4)

式中，Kurt(s)為零均值濾波信號s的峭度；N為信號長度；s[i]為s的第i個分量。

BUZZONI等[22]證明了在一定條件下，峭度與微分熵成相反關系。齒輪、軸承在正常運行狀態下，其振動信號近似于高斯白噪聲，信號峭度接近3，而當振動信號中包含由局部缺陷產生的非高斯成分時，信號的峭度會超過3，可見峭度能在一定程度上反映設備的健康狀態。但正如引言中所述，使用峭度作為解卷積指標的缺陷在于，方法傾向于恢復得到單個主導沖擊而非由局部故障引起的沖擊序列，尤其是當測量信號中含有因電流等導致的強沖擊干擾時，這一缺陷會更加明顯。

1.3 其他常見解卷積指標

為解決上述問題，多種解卷積指標被提出并形成新的方法，最常見的包括相關峭度[20]、多點D-范數[21]以及二階循環平穩指標[22]等。

基于故障沖擊的周期性，相關峭度定義為

(5)

其中，Ms為位移數，Ts為故障信號周期，當Ms=1且Ts=0時，相關峭度退化為峭度。MCKD通過最大化濾波信號的CK來求解濾波器，即

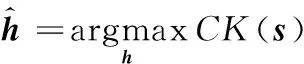
(6)

相比峭度，CK能夠更好地表征沖擊序列，因此MCKD在故障診斷中被廣泛提及。

通過引入目標向量t，設定目標沖擊的位置以及權重，MOMEDA定義了多點D-范數：

(7)

該指標充分考慮了故障沖擊特征的周期性，此外，作為非迭代的求解方法，MOMEDA效率更高。

考慮到旋轉機械局部故障產生的沖擊序列會表現出循環平穩特性，CYCBD采用二階循環平穩指標，定義如下：

(8)

(9)

(10)

其中，k為樣本指數，L為濾波器長度。CYCBD在恢復故障沖擊序列方面表現出非常優異的性能。

由上述指標計算公式可見，這三種常見方法都極大程度上依賴于先驗故障特征頻率，而實際應用中難以預先獲知準確的故障特征頻率，致使方法的適用性受到極大限制。因此，探究不依賴先驗知識的全“盲”方法意義重大。

2 最大重加權峭度盲解卷積方法

為有效恢復故障沖擊序列、準確診斷齒輪故障，本節介紹一種全“盲”方法——最大重加權峭度盲解卷積。信號的重加權峭度計算過程如下：

(1)對濾波信號s進行M等分，得到各子段信號sm(m=1，2，…，M)。

(2)計算各子段信號的峭度Kurtm。

(3)對Kurtm進行升序排列，并將其表示為一行向量的形式，即Kurtasc。

(4)計算Kurtm對其和的權重，即

(11)

(5)對Wm進行降序排列，同樣將其表示為一行向量的形式，即Wdesc。

(6)利用重排后的權重向量Wdesc對重排后的峭度向量Kurtasc進行加權，得到信號的重加權峭度RK：

(12)

根據上述計算過程可見，當M=1時，RK退化為峭度。為直觀呈現RK在表征故障沖擊序列方面的優勢，計算了圖2所示的單個沖擊與周期性沖擊序列(信號長度相同)的RK值。如表1所示，單個沖擊的峭度遠大于沖擊序列的峭度，而單個沖擊的RK遠小于沖擊序列的RK(M>1)，同時沖擊序列的峭度幾乎等于其RK。因此，以重加權峭度作為盲解卷積指標，可有效地解決基于峭度最大化方法傾向于恢復單個主導沖擊的問題。

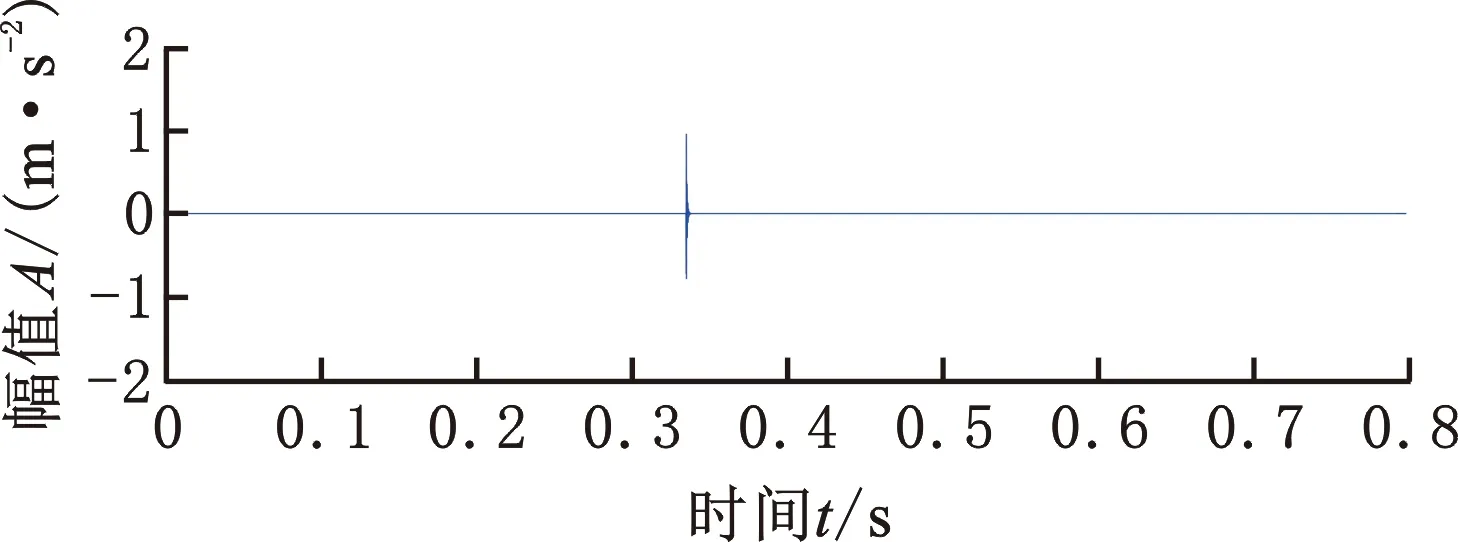
(a)單個沖擊

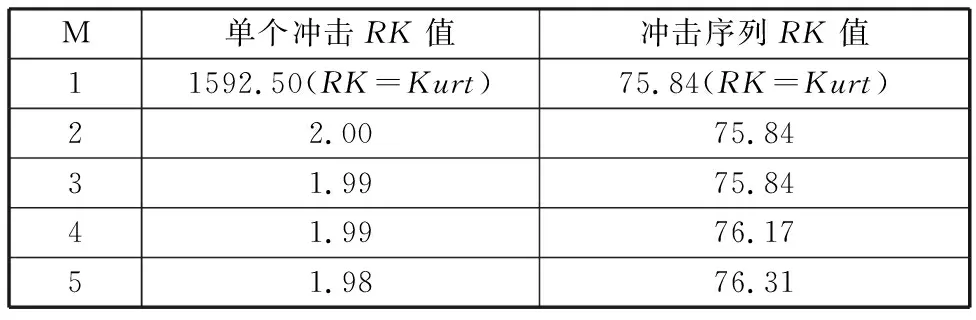
表1 不同M值下單個沖擊與周期性沖擊序列的RK值

M的取值不依賴具體的公式，理論上不超過信號長度的任意正整數都能使算法正常運行，但每一個子段信號長度不能太小，否則子段信號的峭度Kurtm將失去物理意義。對多組仿真信號和實際齒輪振動信號分析后發現，當M=4時，大部分數據分析均能取得理想結果，因此在使用所提方法時推薦M取值為4。

基于上述分析，最大重加權峭度盲解卷積求解FIR濾波器可表示為如下所示的最大化問題：

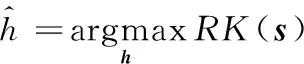
(13)

為求得RK最大值，令RK對濾波器系數的偏導數等于0，即

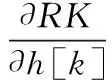
(14)

首先，

(15)

其中，Kurtθ為第θ段濾波信號的峭度，可見，式(14)是高度非線性的，難以直接求解。因此，采用迭代求解法，通過不斷更新濾波器系數的方式求得方程的有效近似解。為簡化運算，令?Kurtθ/?h[k]=0得到M個濾波器，然后對這M個濾波器加權求和即可得到更新后的濾波器，過程如下：

(16)

根據式(2)，有

(17)

(18)

則可得到下式：

(19)

進而，得到其中一個濾波器，則

(20)

(21)

其中，xθ、sθ分別對應第θ段子段信號及其濾波信號，Xθ為xθ對應的Toeplitz矩陣。從而，得到濾波器更新公式：

(22)

綜上，所提方法整體流程如下：

(1)輸入測量信號x，指定參數M=4，隨機初始化濾波器h系數，如h=[0 0 … 1 … 0 0]T。

(2)根據式(2)計算濾波信號s，根據式(12)計算RK(s)。

(3)根據式(22)更新濾波器h系數。

(4)重復步驟(2)和步驟(3)使RK(s)達到最大。

(5)步驟(4)中最大RK(s)對應的濾波信號即為目標濾波信號。

3 仿真信號分析

本節進行仿真信號分析以驗證所提方法對恢復故障沖擊序列的有效性，同時將本領域常見方法(MED、MCKD、MOMEDA以及CYCBD)作為對比研究來探討所提方法的優勢。

考慮到實際測量信號中包含的環境噪聲，以及可能含有強沖擊干擾(如電流干擾)和諧波分量成分，仿真信號x(t)的組成如下：

(23)

式中，s0(t)為故障沖擊序列(頻率為取100 Hz)；b(t)為強沖擊干擾；c(t)為諧波分量；w(t)為信噪比-10 dB的高斯白噪聲；ρ為阻尼系數。

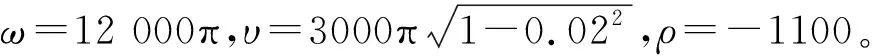
(a)故障沖擊s0(t)

各方法的濾波信號如圖4所示，可見，本文方法與MCKD、MOMEDA以及CYCBD均準確恢復了故障沖擊序列，而MED只得到單個主導沖擊。然而，正如1.2節所述，MCKD、MOMEDA和CYCBD作為非全“盲”方法，需要提前指定待恢復沖擊序列的頻率，而圖4中的分析結果正是建立在指定頻率完全等于待恢復沖擊序列頻率基礎之上的。為進一步探究這三種方法對故障頻率這一先驗的依賴特性，圖5給出了它們在指定頻率為103 Hz時的濾波信號。可見，即便是指定頻率與故障沖擊序列實際頻率存在較小偏差時，這三種方法均無法有效恢復故障沖擊序列。

(a)本文方法

由上述分析可見，與同為全“盲”的經典MED相比，所提方法解決了MED傾向于恢復單個主導沖擊的問題，在恢復故障沖擊序列中表現出更好的潛力。而相較于常見非全“盲”的MCKD、MOMEDA以及CYCBD，本文方法在保證分析結果準確的基礎上，不需要有關故障沖擊的先驗條件，在實際應用中具有更強的適用性。

(a)MCKD

由于實際場景中測量信號還可能同時包含多個沖擊干擾，因此在上述仿真信號x(t)的基礎上再添加多個沖擊干擾b′(t)(具體參數如表2所示)，得到新的仿真信號x′(t)。b′(t)的表達式為

(24)

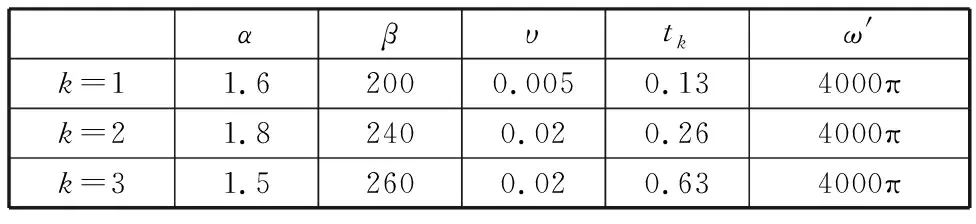
表2 b′(t)的具體參數

b′(t)和x′(t)波形分別如圖6a、圖6b所示，可見，仿真信號中的沖擊干擾較為明顯。如圖6c所示，所提方法仍準確恢復了故障沖擊序列，驗證了本文方法對分析存在多個沖擊干擾的信號的有效性。

(a)多個沖擊干擾b′(t)

4 風電機組故障診斷應用研究

工程應用中，由于環境噪聲以及其他干擾的影響，測量信號組成十分復雜，使得故障診斷具有一定難度。本節采用風電機組故障診斷實際案例分析，來驗證本文方法在實際復雜工程應用中的有效性，同時與MED進行對比研究。因上述其他方法均依賴故障頻率這一先驗條件，而實際信號的故障頻率難以準確獲知，因此本案例中不再將它們作為對比方法。

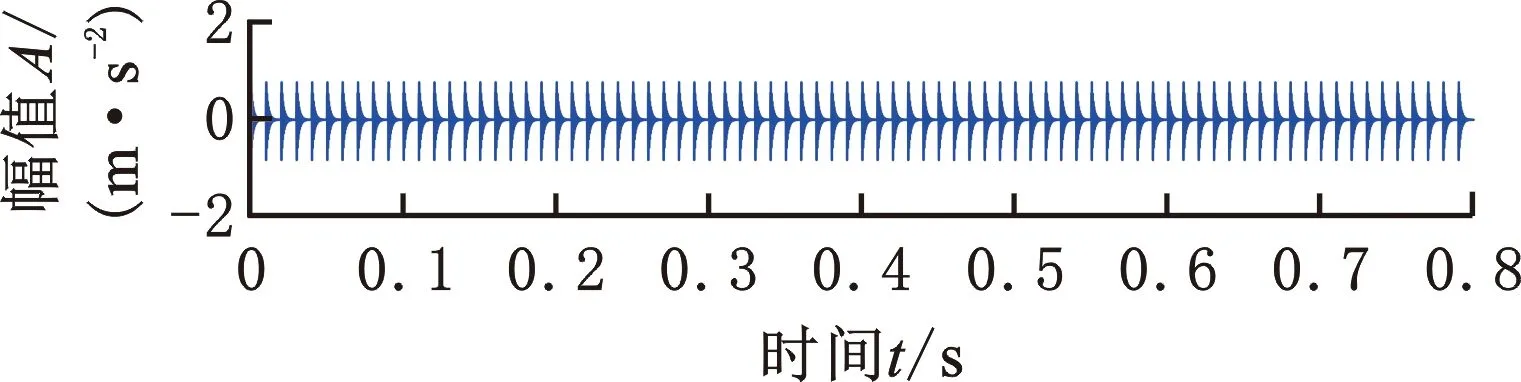
本工程數據來自于某風電機組振動監測，振動監測中，安裝在齒輪箱輸出小齒輪軸上方殼體表面的加速度傳感器(圖7)監測到了異常振動。信號采樣頻率為97 656 Hz，轉速計測得齒輪箱輸出小齒輪軸轉速為1800 r/min。截取信號51 200點以分析異常振動出現的原因，如圖8a所示，由于測量信號波形中觀察不到任何故障特征信息，故無法對異常振動做出有效診斷。

圖7 風電機組傳動系統及齒輪箱輸出軸小齒輪的加速度計測點位置示意圖Fig.7 Schematic diagram of wind turbine transmission system and accelerator location of the output pinion gear

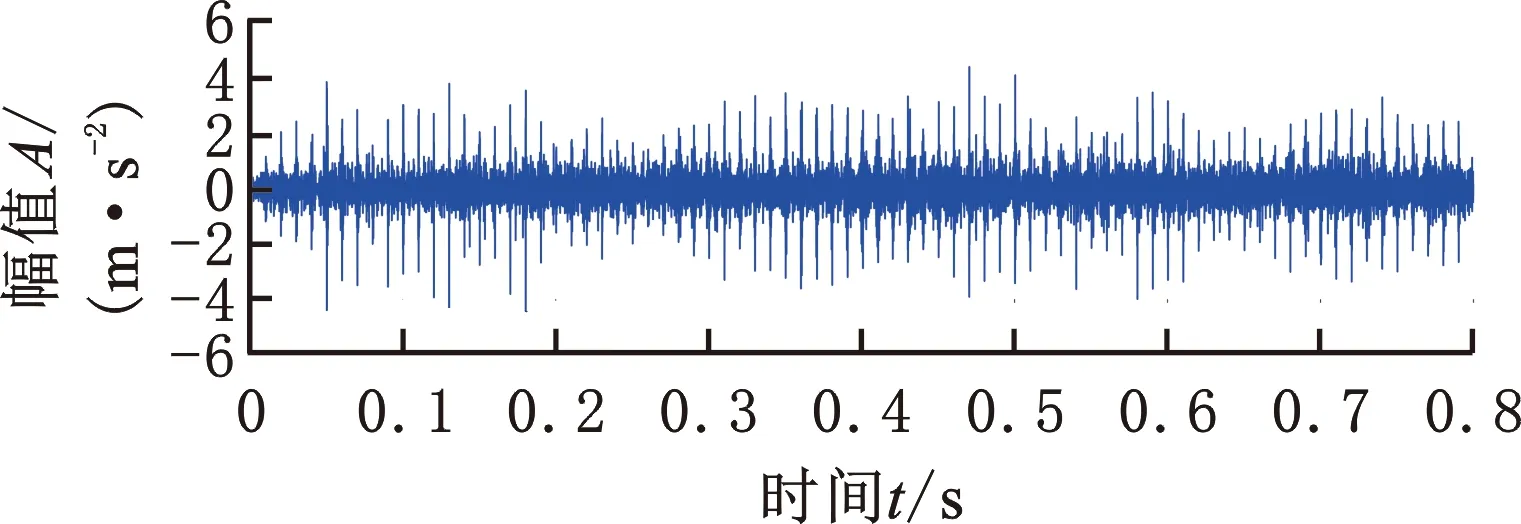
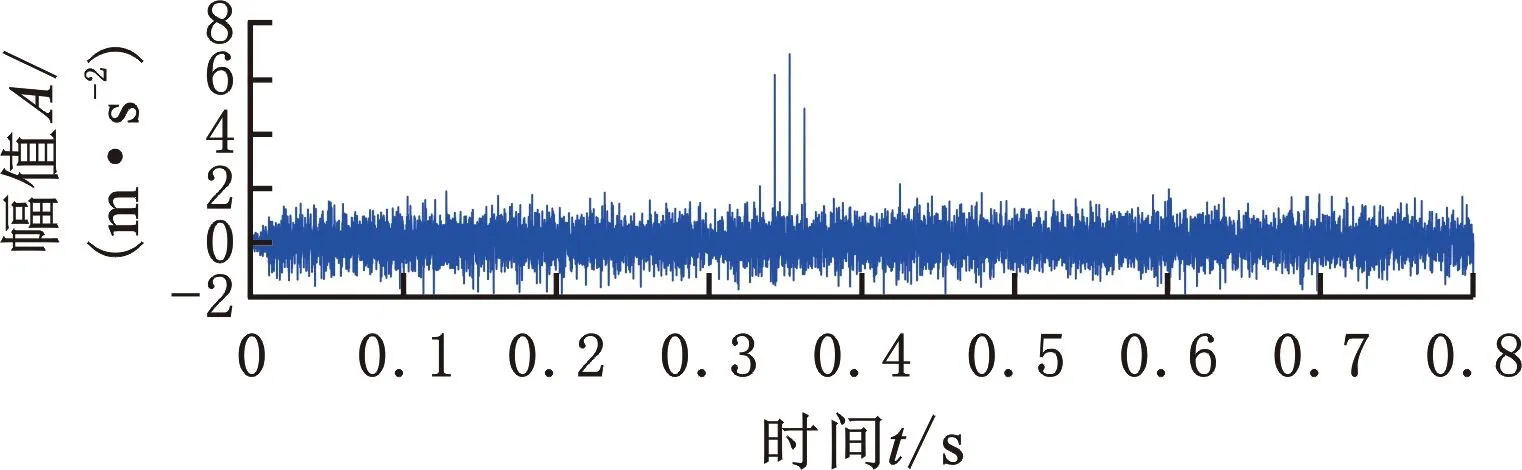
本文方法與MED的濾波信號分別如圖8b、圖8c所示，同時濾波信號對應的包絡譜分別如圖9a、圖9b所示。根據濾波信號，本文方法恢復得到的周期性沖擊序列的頻率為29.6 Hz(1/0.0338 Hz)，十分接近輸出小齒輪理論故障特征頻率(30 Hz)。此外，在其濾波信號的包絡譜中，可以清楚地觀察到小齒輪故障特征頻率及其多組倍頻。因此，可初步認為小齒輪存在故障。在之后的停機開箱檢測中發現輸出小齒輪某一輪齒確已出現損傷(圖10)，驗證了本文方法的有效性。相比之下，MED的濾波信號卻得到的是單個主導沖擊，如圖8c所示。并且，在其濾波信號的包絡譜中只有故障頻率處的譜線比較明顯，無法觀察到其他倍頻成分，如圖9b所示，因此仍難以對異常振動做出準確可靠的診斷。

(a)測量信號

(a)本文方法濾波信號的包絡譜

圖10 齒輪箱輸出小齒輪輪齒損傷Fig.10 The localized damage on the output pinion gear

5 結論

(1)提出了最大重加權峭度盲解卷積方法，解決了基于峭度最大化解卷積方法傾向于恢復單個主導沖擊的問題，并且作為一種全“盲”方法，不需要有關故障沖擊序列的先驗知識，較非全“盲”方法具有更強的適用性。

(2)仿真信號分析以及風電機組故障診斷應用研究驗證了所提方法的有效性，同時與傳統盲解卷積方法(MED、MCKD、MOMEDA和CYCBD)的對比結果進一步凸顯了所提方法的優勢。