基于位移影響線的城市立交橋拓寬改造研究
宋文鋒,唐春龍
(重慶中煤科工工程技術咨詢有限公司,重慶 400042)
隨著城市建設的快速發展,原立交橋難以滿足日益增長的交通發展要求。為緩解交通壓力,對原橋結構進行拓寬改造。城市立交橋拓寬改造常采用上下部結構相互不連接、上下部結構相互連接、上部結構連接下部不連接等拓寬方法。第一種拓寬方法中,上下部結構相互不連接,新舊橋結構之間設置工作縫,各自受力明確、互不影響,施工難度小,因而在城市立交橋拓寬改造中得到廣泛應用。由于原立交橋以簡支橋梁結構為主,為滿足橋下凈空要求,新舊橋梁不能采用同跨度布置,通常采用連續梁橋,以降低梁高,同時新舊橋梁上下部結構相互不連接,故新舊橋梁結構不同,導致新舊橋剛度不匹配、變形不協調,在活荷載作用下將產生豎向變形差異。為此,該文基于位移影響線精確分析新舊橋梁的變形差,為城市立交橋拓寬改造設計提供依據。
1 位移影響線
橋梁位移影響線是單位移動荷載作用下某截面位移變化曲線,采用靜力法繪制。該文結合橋梁結構形式,采用撓度公式[見式(1)]進行跨中位移影響線繪制。
(1)

1.1 簡支梁跨中位移影響線
采用圖乘法計算,得到簡支梁跨中位移影響線方程[見式(2)],據此繪制的簡支梁跨中位移影響線見圖1。

圖1 簡支梁跨中位移影響線
(2)
1.2 連續梁中跨跨中位移影響線

(3)
由式(3)得X1=X2=-3L/40。分別計算單位移動荷載p=1作用下左邊跨、中跨和右邊跨彎矩。1)當p=1作用于左邊跨時,根據圖2(b)和圖2(c),采用圖乘法計算中跨跨中位移影響線,結果見式(4)。2)當p=1作用于中跨左側時,根據圖2(b)和圖2(d),采用圖乘法計算中跨跨中位移影響線,結果見式(5)。3)當p=1作用于中跨右側時,根據圖2(b)和圖2(e),采用圖乘法計算中跨跨中位移影響線,結果見式(6)。4)當p=1作用于右邊跨時,根據圖2(b)和圖2(f),采用圖乘法計算中跨跨中位移影響線,結果見式(7)。
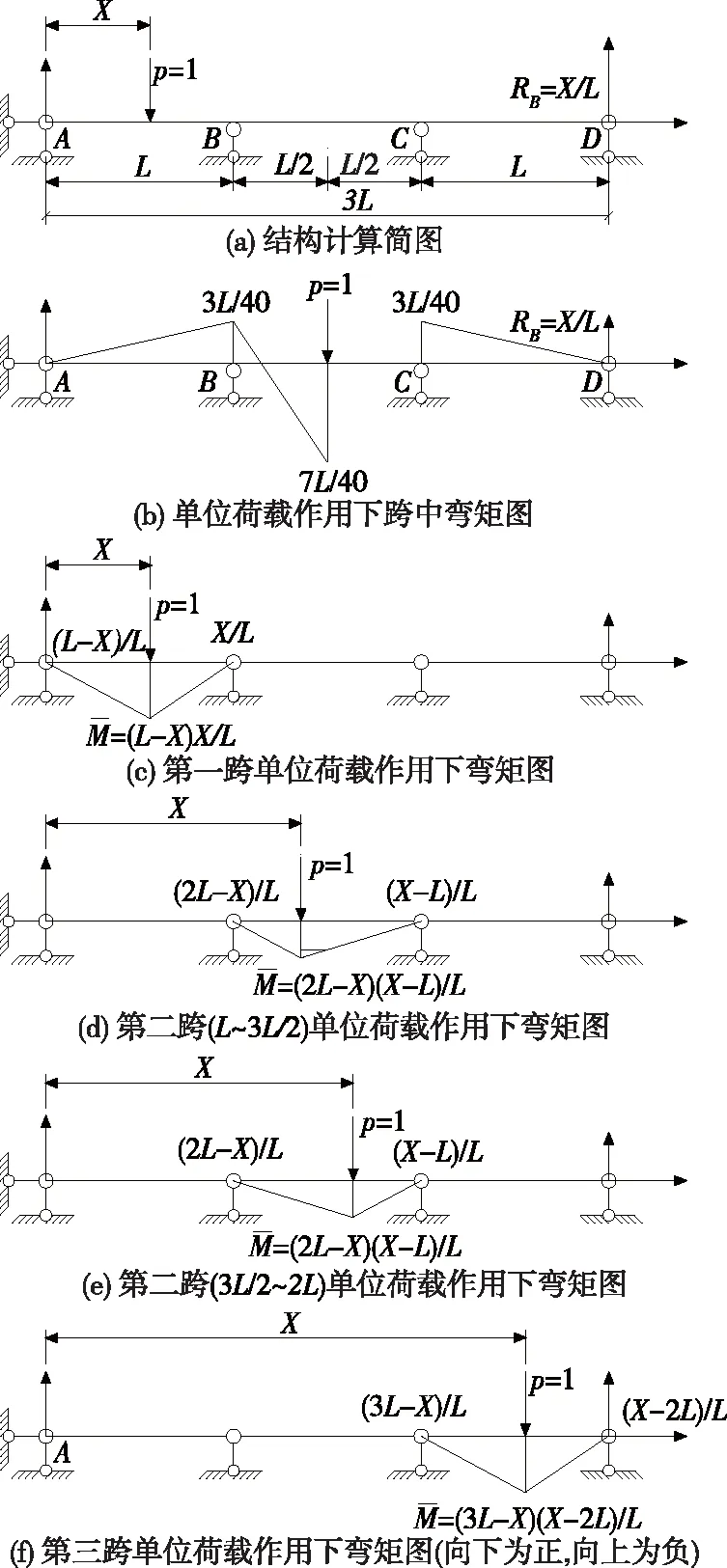
圖2 連續梁結構受力示意圖
(4)


72L2X-23L3),L≤X≤3L/2
(5)


198L2X-112L3),3L/2≤X≤2L
(6)

2L≤X≤3L
(7)
根據位移影響線方程(3)~(7)繪制的連續梁跨中位移影響線見圖3。

圖3 連續梁中跨跨中位移影響線
2 汽車荷載產生的位移
2.1 汽車荷載
汽車荷載分為城-A級、城-B級兩個等級。城-A級車道荷載的均布荷載標準值qk為10.5 kN/m;集中荷載標準值Pk如下:橋梁計算跨徑L≤5 m時Pk=270 kN,L≥50 m時Pk=360 kN,L為5~50 m時Pk=2(L+130)kN。城-B級荷載按城-A級荷載的75%選取。
2.2 位移計算
根據車道荷載及位移影響線方程(2)、(4)~(7)計算車道荷載、自重作用下橋梁結構的位移。對于簡支梁,車道荷載、自重作用下橋梁結構位移為:
(8)
對于連續梁,車道荷載、自重作用下橋梁結構位移為:
(9)
3 工程實例
3.1 工程概況
某立交現狀為六路立體交叉的單喇叭形式,為緩解立交區域交通壓力,對該立交進行改造,采用主線橋梁兩側拓寬改造的方式。主線橋跨布置為(2×30)m+39.5 m(上跨橋)+(6×30)m預應力混凝土簡支梁,橋梁全長288 m,30 m T梁高2.0 m,39.5 m T梁高2.5 m,均采用預制吊裝,橋面寬31 m。受下穿道路的影響,拓寬橋梁橋跨布置為[45 m+45 m(上跨橋)+45 m]連續鋼箱梁橋+(5×30)m預應力混凝土連續梁橋,梁高2.1 m,橋面寬10.5 m(見圖4)。

圖4 拓寬橋梁斷面示意圖(單位:cm)
3.2 新舊橋梁變形計算分析
舊橋計算跨徑為38.5 m,新橋邊跨計算跨徑為44.5 m、中跨計算跨徑為45.0 m。由于舊橋的材料及剛度已定,通過調整新橋的材料特性及剛度使新舊橋梁在汽車荷載作用下產生的位移基本相等,位移計算見表1。
根據表1,在新橋結構材料特性及梁高一定的情況下,可通過調整新橋結構剛度使新舊橋梁結構的位移基本相等,從而確保行車舒適,減少后期維護維修工程量,同時提高設計效率。

表1 新舊橋梁位移計算
4 結語
基于城市立交橋拓寬改造的特點,利用圖乘法推導橋梁結構位移影響線,并計算汽車荷載作用下最大位移。以某城市立交橋拓寬改造工程為依托,在舊橋位移、新橋材料特性及梁高為定值的情況下,通過調整新橋結構剛度使新舊橋梁結構位移基本相等,確保行車舒適,減少后期維護維修工程量,增強橋梁結構的耐久性,同時提高設計效率。

