鋼板筒倉靜態貯料側壓力有限元分析

李 進，莊 磊，徐 佩

(1.中南電力設計院有限公司，武漢 430071；2.武漢理工大學道路橋梁與結構工程湖北省重點實驗室，武漢 430070)

鋼板筒倉是儲存水泥、糧食等散料的薄壁結構，在諸多領域中發揮著重要的作用。它可以長期儲存各種能源或原料，在生產原料的加工運輸方面提供至關重要的緩沖和調節作用。鋼板筒倉的結構形式決定了它具有節約用地、自重輕、倉儲量大、自動化程度高等優點，相比于鋼筋混凝土筒倉，鋼板筒倉施工時間短且鋼材可回收使用，具有明顯的經濟優勢。隨著世界經濟的發展和人民生活水平的提高，對筒倉安全問題的研究也越發迫切[1]。

貯料側壓力的存在是筒倉結構區別于其他結構形式的關鍵，由于散體材料本身物理特性比較特殊，使得筒倉側壓力的分布很難用一個統一的數學模型來描述。為了筒倉結構設計更加規范，提高筒倉在工程應用中的安全性和穩定性，世界各國的學者在貯料側壓力分布方面做了大量的研究。

1895年，Janssen[2]通過筒倉散料同一水平面的豎向壓力相等，且貯料各點的豎向壓力與水平壓力之比為一常數這一假定，建立貯料的靜力平衡方程，得出靜態筒倉側壓力的計算公式。盡管該公式因為假設的存在而有著局限性，且只適用于靜態條件下的側壓力計算，但是它仍然有著不可忽視的指導意義。

通過試驗可以更直觀地研究筒倉側壓力的分布，然而試驗法往往比其他方法耗費更多的人力物力，并且很難獲得通用的數學模型，這使得試驗法的應用受到了限制。

隨著科學技術的發展和時代的進步，數值模擬憑借著方便快捷、經濟實惠、求解可靠、易于參數化分析等優點受到了廣泛的關注。論文采用大型有限元分析軟件ANSYS建立三維簡易平底倉模型，探究貯料側壓力在鋼筒倉倉壁的分布。

1 數值模型

1.1 散料的本構

散體材料的力學特性非常復雜，它既具有一定的流動性，又能在一定范圍內保持它的堆積形狀[3]。散體的這種基本屬性類似于液體與固體的結合，很難用準確完善的理論來描述，采用有限元法對貯料進行分析時，各國學者嘗試過多種不同本構模型。目前被最廣泛應用于土力學和散粒物料研究的是Drucker-Prager屈服準則和Mohr-Coulomb屈服準則。D-P模型是一種彈性完美的塑性行為，可以考慮膨脹效應，克服了Mohr-Coulomb屈服準則在計算塑性應力時的奇異現象，其屈服面表達式為

F=αI1+J2-σ

(1)

式中,I1為第一應力不變量；J2為第二偏應力不變量；α、σ為材料參數。

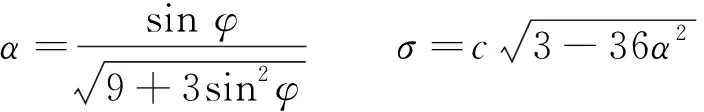
式中：φ為散料有效內摩擦角；c為材料黏性系數。

在D-P模型的參數設置中，因為大多數貯料一般無粘聚力，而直接將黏性系數設為0可能會產生數值奇異，所以通常將材料黏性系數c設為一個很小的數值。另外，膨脹角ψ是反映貯料塑性變形的一個重要參數，ψ=0°時，為不可壓縮材料，文章不考慮貯料的膨脹效應，所以膨脹角設為0。

1.2 散料與筒倉壁的接觸模擬

貯料對鋼筒倉的作用包含水平側壓力和豎向摩擦力兩部分，規范對其標準值計算均有明確規定。而在分析貯料與筒倉的相互作用時，將貯料等效為荷載，不能體現出兩者的相互作用，需借助有限元方法進行分析。貯料與筒倉的相互作用通過設置接觸來模擬，接觸分析屬于高度非線性分析[4]。目前，常見的接觸類型有兩種：1)剛-柔接觸：一種軟材料和一種硬材料接觸時，可假定為剛-柔接觸。2)柔-柔接觸：兩個接觸體都是變形體，剛度相近。

論文只探究在靜態條件下鋼筒倉倉壁的側壓力分布情況，不考慮倉壁的變形，所以采用剛-柔接觸來模擬。

在筒倉摩擦模擬中使用面面接觸。為此，一旦生成存儲材料所代表的體積并進行網格劃分，選擇圓柱輪廓區域(顆粒壁摩擦區域)和在十分之一毫米(0.1 mm)距離處生成的平行區域來模擬筒倉壁面(圖1)。有限元分析中，貯料采用實體單元(SOLID65)模擬，筒壁采用殼單元(SHELL63)模擬。選擇筒倉壁面的區域，用ANSYS程序的TARGET170單元進行摩擦網格劃分，TARGET170單元為目標單元，設置在鋼筒壁內側，其網格單元與殼單元的網格劃分保持一致；選擇顆粒摩擦區域并與CONTACT 173單元進行網格劃分，CONTACT173單元為接觸單元，設置在貯料單元外側，其網格單元與實體單元的網格劃分保持一致。另外，殼單元和實體單元的網格劃分相一致，便于形成接觸對。接觸單元如圖2所示。

1.3 有限元模型

假設筒倉壁的材料為Q235鋼，密度ρ=7 850 kg/m3，彈性模量E=2.01×1011Pa，不考慮鋼材的塑性。假設貯料為水泥，具體的材料參數見表1。

建立不同高徑比的簡易平底倉有限元模型，其中淺倉倉壁高度10 m，深倉高度20 m，兩者的直徑皆為10 m，倉壁厚度0.01 m。以淺倉為例，筒倉倉壁和貯料的網格劃分如圖3所示，倉壁的網格劃分與貯料側面相對應，在筒倉底部添加固定約束，對貯料施加重力荷載[5]。

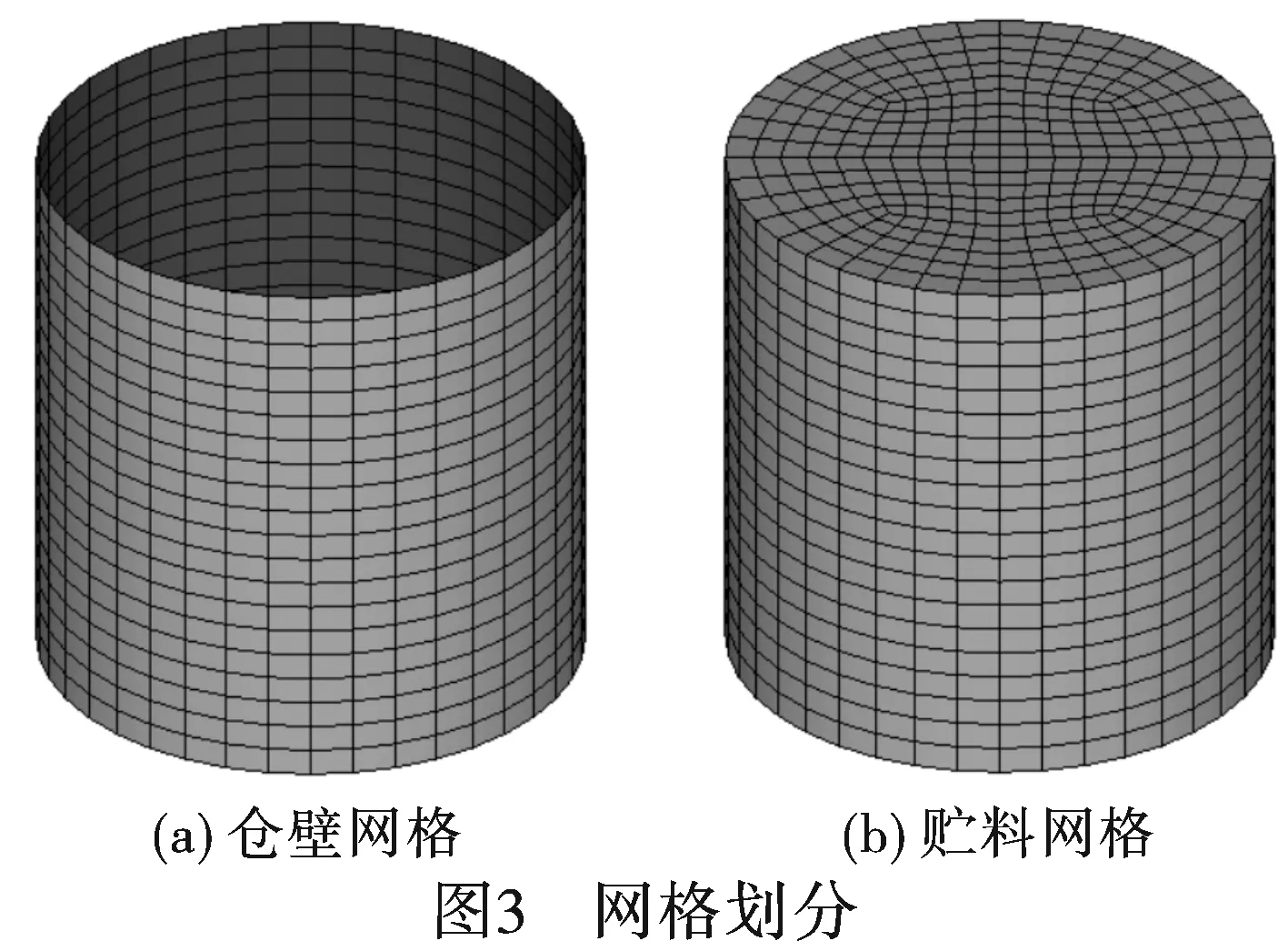
2 有限元分析結果

2.1 淺倉靜態貯料側壓力

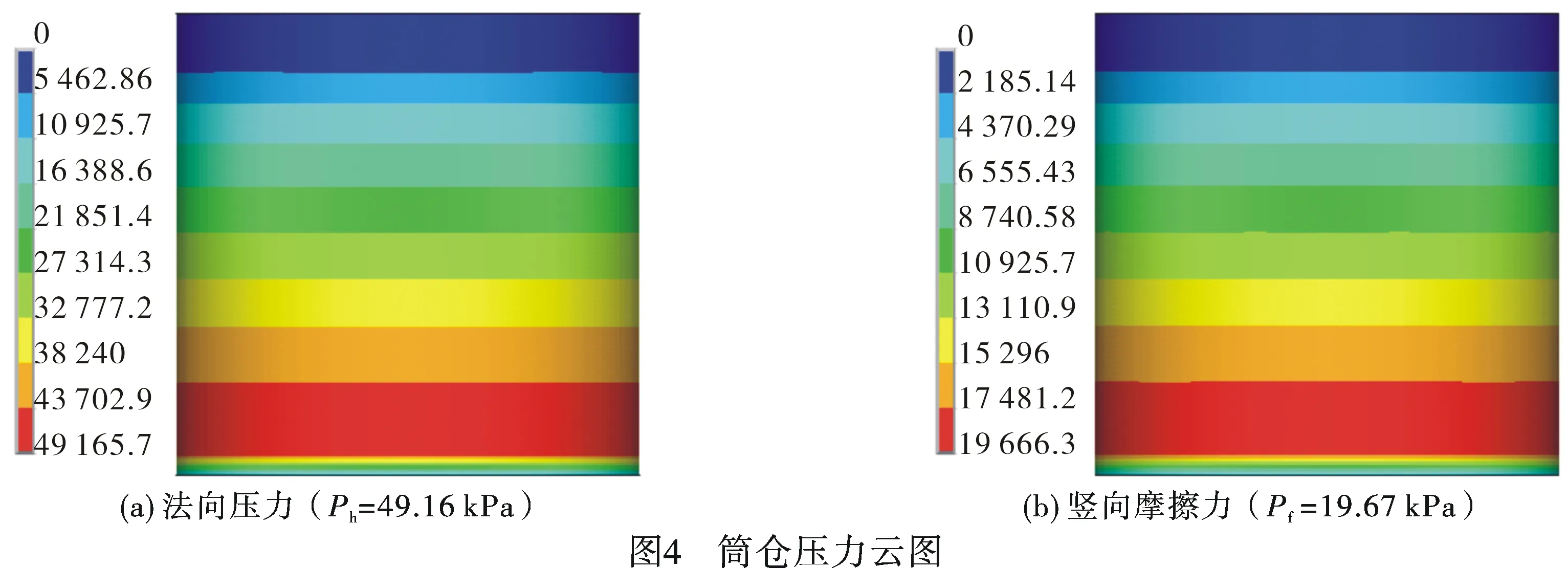
由有限元云圖(圖4)可知，筒倉側壓力從倉頂隨著深度的增加而加大，在靠近倉底處達到最大值，此處筒倉的側壓力為49.16 kPa。查閱規范[6]，根據規范提供的公式可以得知，規范算得的最大側壓力在筒倉最底部，大小為45.14 kPa。貯料豎向摩擦力同樣在靠近倉底處達到最大值，最大豎向摩擦力為19.67 kPa，根據規范計算得到的值為18.05 kPa。所以有限元的計算結果與規范計算結果相近。

2.2 深倉靜態貯料側壓力

深倉的壓力分布與淺倉的相似，法向壓力在靠近倉底處達到最大值52.48 kPa，豎向摩擦力在倉底處的最大值為21.65 kPa，規范算得的最大法向壓力為58.42 kPa，最大豎向摩擦力為23.37 kPa，吻合良好。

3 結 語

從有限元的分析結果可以看出，深倉和淺倉的側壓力從倉頂隨著深度的增加而加大，在靠近倉底處達到最大值，有限元的計算結果與根據規范計算的值基本吻合，說明有限元模擬較為準確。另外，有限元模擬的筒倉側壓力在筒倉底部有下降段，而規范計算的側壓力是隨筒倉深度遞增的，兩者之間的差異可能是有限元分析中貯料底部邊界條件的設置與實際不符，需要更加深入的研究。