基于數據挖掘的航道開挖過程中鄰近橋墩變形預測

汪 彥 張 薇 余 杰 顧禎雪 宋德威 孫 陽,3,4

(1.杭州京杭運河二通道建設投資有限公司,杭州 330104;2.河海大學 港口海岸與近海工程學院,南京 210098;3.河海大學 淮安研究院,江蘇 淮安 223001;4.河海大學 海洋與近海工程研究院,江蘇 南通 226000)

結構物的變形量能夠真實反映周圍土體受到擾動后的響應結果,地下工程由于隱蔽性強,土體和結構物的變形不易觀察,各結構物之間的變形、受力特性的關聯性難以摸清.隨著可編程計算機技術的進一步發展,人工智能數據挖掘方法逐漸被運用到現場測試數據分析領域,用層次化的概念體系來整合理解規律.

Agrawal等[1]最早提出關聯法則,Agrawal等[2]提出了實現關聯規則的Apriori算法,此后許多學者對關聯規則的挖掘和算法的改進進行了研究[3-5],并從避免局部陷入鞍點、加快收斂速度、提高網絡容錯率、引入新的智能算法[6-8]等方面進行了優化.近年來國內外學者傾向于將數據挖掘應用于邊坡變形預警、深基坑開挖穩定性分析、基坑對鄰近構筑物的安全評估與風險控制等實際工程[9-18],對結構物的響應做出合理預測,并對發生的原因進行解釋.

目前將數據挖掘應用于航道下穿高鐵工程中的案例較少,常用的數據分析方法所依賴的假設缺乏嚴格的理論指導,僅是一種經驗規則,缺乏客觀性.本文結合京杭運河二通道(杭州段)下穿滬昆高鐵工程,建立了橋墩變形量的一維響應預測模型和多維響應預測模型,驗證數據挖掘技術在該實際工程中的可行性.達到降低施工風險、有效指導施工的目的,進而為類似工程中結構物的變形預測提供有效方法.

1 響應模型的建立原理

1.1 GM(1,1)模型

GM(1,1)在實際工程應用中比較廣泛,具體的模型建立方法如下:

首先對原始數據X(0)進行累加,弱化其波動性和隨機性,接著根據灰色理論,對累加后的數據X(1)建立關于時間t的白化形式一階一元微分方程:

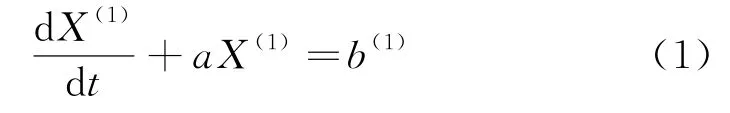
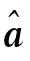
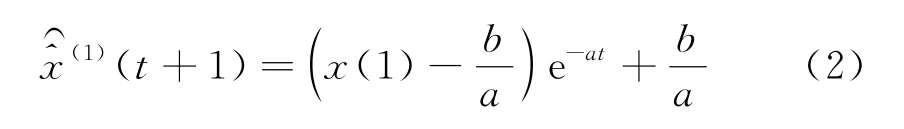
將其離散化得到白化響應式:

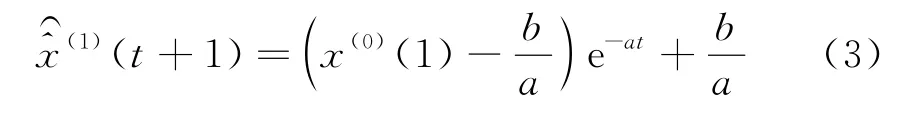
最后進行累減還原得到預測值:

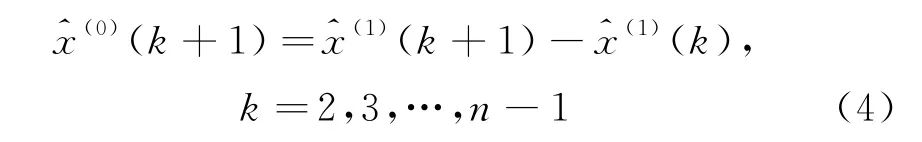
1.2 GM(1,n)模型

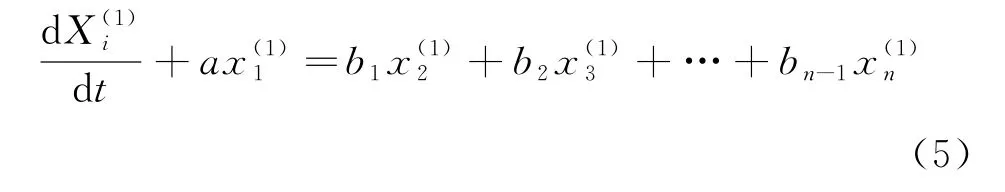
將上述公式離散化,并構造矩陣形式的微分方程:

最后對式(7)經過累減還原即可對原始序列進行擬合和預測.

1.3 殘差修正

假設灰色模型預估值與原始序列之間的殘差序列如下:

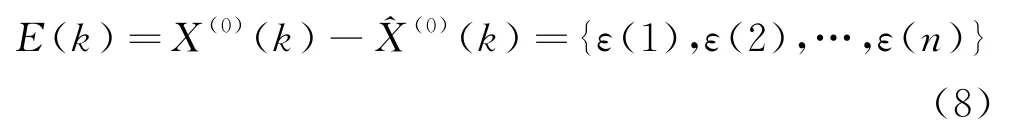
對原始殘差序列進行正化處理,并利用波形數據生成法將處理后的結果轉化為單調遞增序列,記為E2(k).

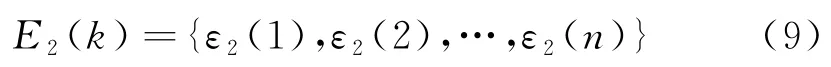
式中:ε1(k)=ε(k)+2|minε(k)|,ε2(k)=ε1(k)+d(k),k=1,2,…,n.

若一次殘差修正后的模型精度仍不滿足要求,可重復進行多次修正,直至預測模型的誤差滿足限定的要求.

2 橋墩變形預測

2.1 工程概況

京杭運河二通道(杭州段)新開挖航段,是京杭運河三級航道整治工程中投資最大的部分,也是建設的難點和重點,項目全長26.4 km,于航道里程K26+682處下穿滬昆高鐵,如圖1所示.

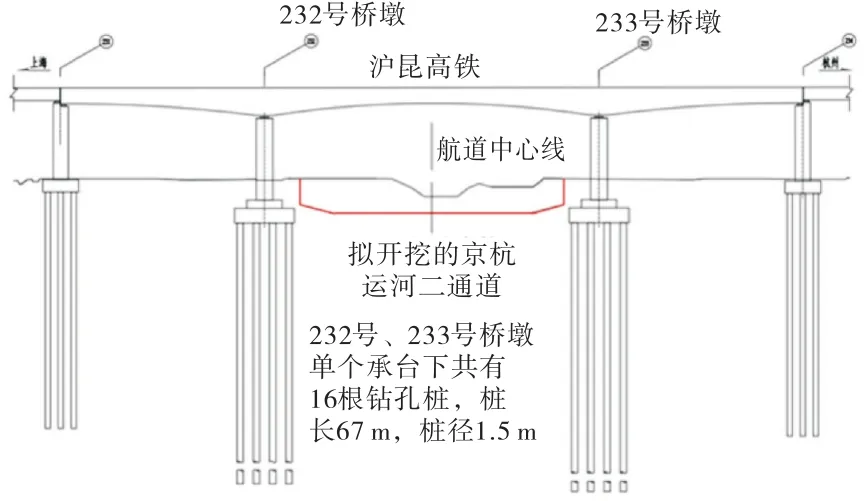
圖1 下穿段受影響橋墩

受新建航道影響,為防止航道兩側鄰近橋墩因土體開挖釋放單側約束而造成的基礎與橋墩側向偏移,保證客運專線的結構及運營安全,需對滬昆高鐵海杭特大橋京杭運河橋段48+80+48 m 連續梁中墩232號橋墩和233號橋墩的位移量進行密切關注.

2.2 基于GM(1,1)模型的一維響應模型

2.2.1 模型可行性驗證

選擇232號橋墩墩頂豎向位移測量值作為原始數據,共提取22個值,選擇前5個數據作為原始序列模擬橋墩的豎向位移發展情況,接著與測量結果對比,進行灰色模型預測可行性的驗證.

設X(0)為橋墩墩頂豎向沉降的原始序列,則:X(0)={-0.723,-0.712,-0.679,-0.648,-0.645}.

對原始序列進行平滑性檢驗,令σ(0)(k)為X(0)在k點的級比:

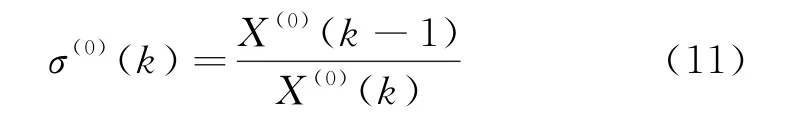
橋墩墩頂豎向沉降的級比序列為:σ(0)(k)={1.015,1.049,1.048,1.005}.σ(0)(k)屬于區 間[1.005,1.049].令μ為測度,則有:μ[1.005,1.049]=|1.049-1.005|=0.044,此時μ＜0.2,可以認為橋墩墩頂豎向沉降的原始序列X(0)是光滑序列.

2.2.2 模型計算與分析

橋墩墩頂豎向沉降的原始序列為X(0)={-0.723,-0.712,-0.679,-0.648,-0.645},計算出a=0.0349,b=-0.7440.代入式(3)和式(4)可得離散化的白化響應式為:

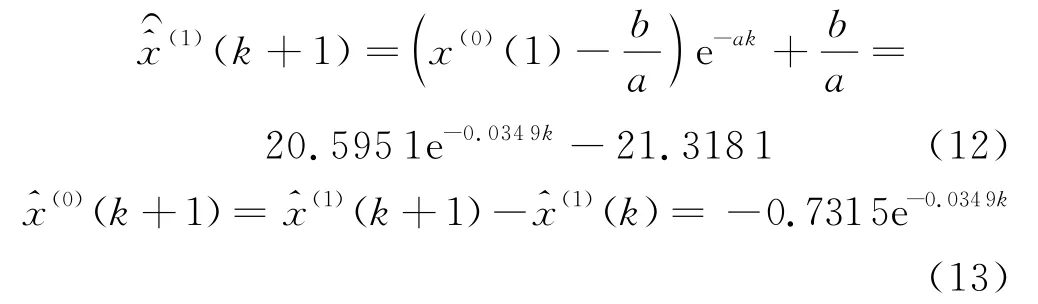
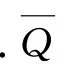
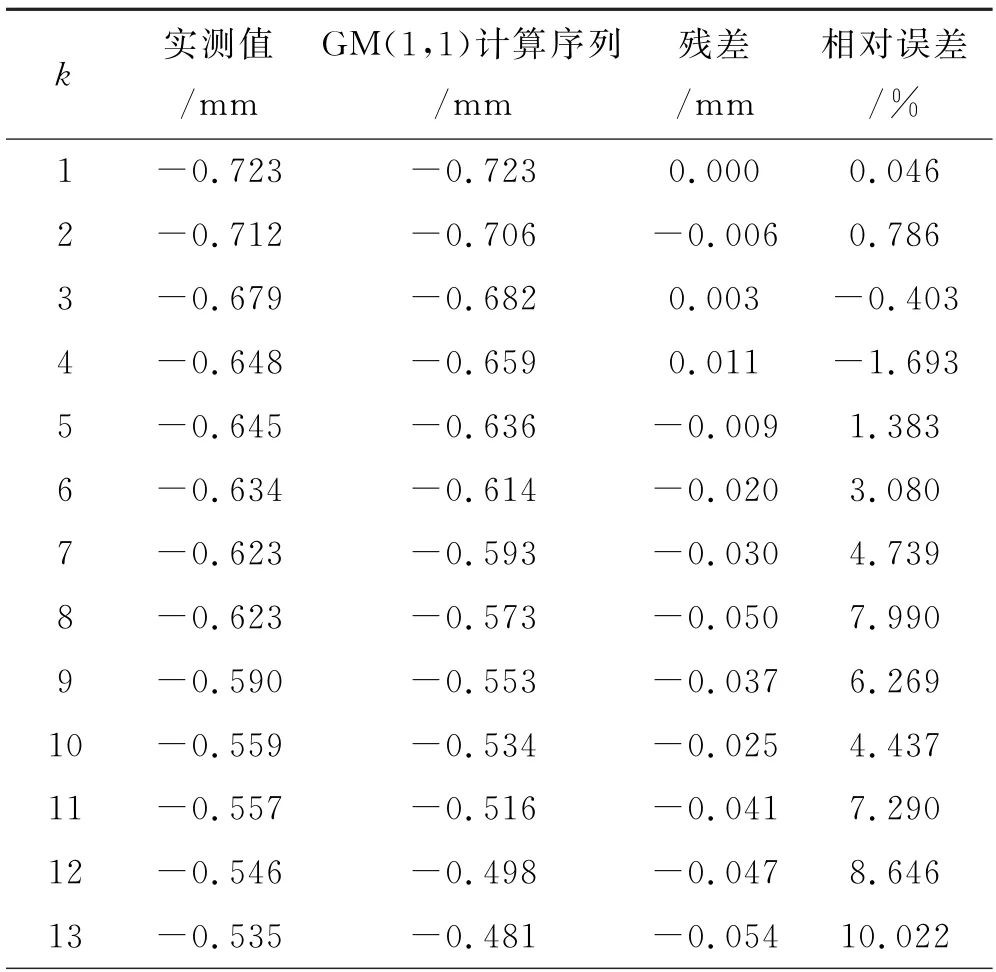
表1 基于5數值的計算結果與誤差檢驗

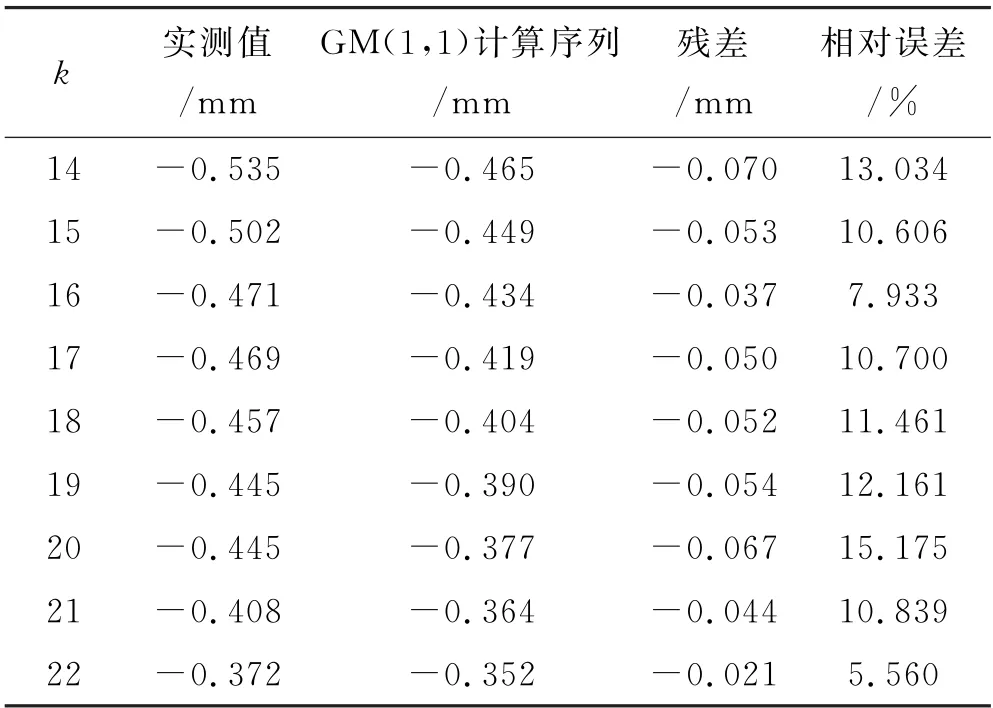
續表1 基于5數值的計算結果與誤差檢驗

經過初步分析,發現緊鄰原始序列的預測值相對誤差較小,精度較高.因此考慮減小預測值的個數,將精度較高的、臨近原始序列的預測值加入原先的原始序列,剔除位于原始序列前端等數量的數值,組成新的二次序列作為原始序列,采用等維灰數遞補模型進行橋墩墩頂豎向位移的預測,計算結果見表2.

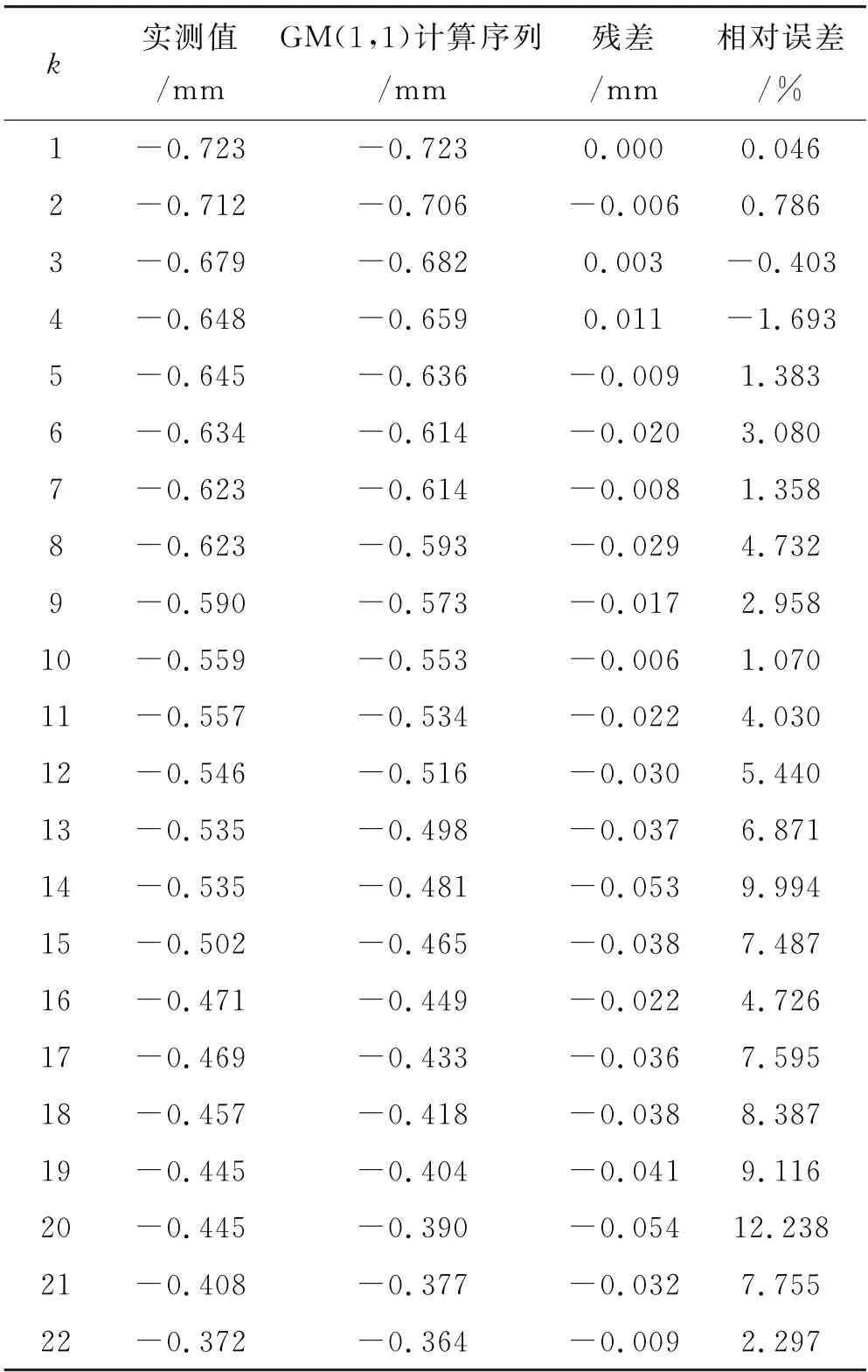
表2 基于等維灰數遞補模型的5數值計算結果與誤差檢驗

為了研究不同原始序列個數對灰色模型的預測精度的影響,再分別取前8個原始數據和前10個原始數據作為原始序列進行計算,不同模型的計算結果誤差比較如圖2～3所示,可以看出預測的相對誤差在0.046%至2.5%之間.

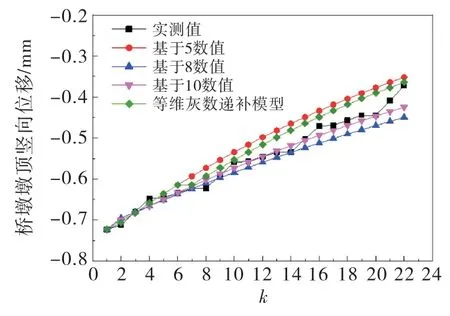
圖2 橋墩墩頂豎向位移預測結果比較

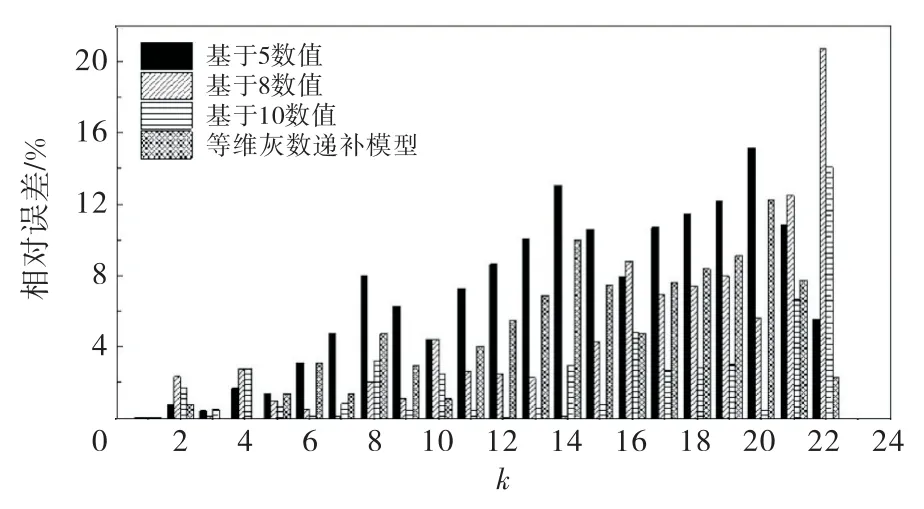
圖3 橋墩墩頂豎向位移預測誤差比較

對比可以發現灰色模型的預測精度隨著原始數據的增加而增加,且高精度預測值集中在原始序列之后的幾個值中,越往后誤差越大.等維灰數遞補模型在原始序列數目不變的情況下,能顯著提高小樣本灰色模型模擬的精度.

2.3 基于關聯法則聯合GM(1,n)模型的多維響應模型

2.3.1 關聯法則挖掘相關因素

灰色系統目標變量為橋墩墩頂豎向位移,相關變量航道中心坑底豎向位移,內、中間和外圍護樁樁頂的豎向位移和水平位移,內橫撐軸力,外橫撐軸力,近外圍護樁的地表沉降以及橋墩墩頂豎向位移,分別用A、B、C、D、E、F、G、H、J、K和X表示.每組均有8個數據.假設該數據為8周內的數據,計算每周的變化率.為了消除不同類別對象變化速率的差異,便于分析和比較,使用最大值最小值區間劃分的方法,通過式(14)將各監測項目的變化速率均局限在[0,1]區間內:

對各監測項目的速率大小進行分類,分類方式見表3.

表3 監測項目速率變化分類

當監測項目的變化速率為中等即以上時,假定該監測項目變化較為顯著.列出關于時間的顯著變化數據庫事務列表,見表4.

表4 數據庫的事務列表

假定強關聯規則的最小支持度閾值min_Support=30%,最小置信度閾值min_Confidence=70%.邏輯蘊涵式A?B的含義為在數據庫中,A的發生與B有關.經計算,與橋墩墩頂豎向位移X有關的頻繁項集為{AX}、{BX}、{CX}以及{BCX},其中B?X、C?X以及BC?X的置信度均為75%,大于min_Confidence=70%,根據Apriori算法,上述關聯法則為強關聯法則,表示當橋墩墩頂豎向位移變化速率較大時,內圍護樁和中間圍護樁的樁頂豎向位移變化速率也較大,他們的關聯度較為緊密.因此可以將內圍護樁和中間圍護樁的樁頂豎向位移作為GM(1,n)模型的相關序列代入計算.

2.3.2 GM(1,n)模型計算與分析

模型相關因子個數為2,取前5周的數據作為原始序列進行計算預測,即每個序列的長度為5.因此取橋墩墩頂豎向位移、內圍護樁和中間圍護樁的樁頂豎向位移作為變量建立GM(1,3)模型.

計算出a=-0.2680,b1=-14.6112,b2=25.4977,進而得出GM(1,n)模型下的橋墩墩頂豎向位移,計算結果見表5.

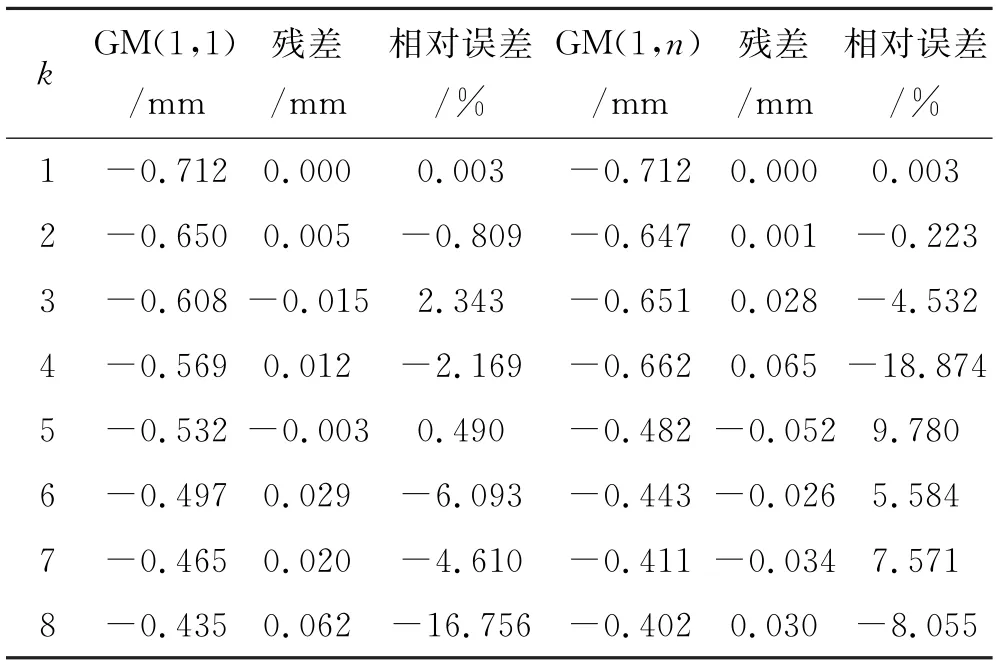
表5 基于GM(1,1)模型和GM(1,n)模型的橋墩墩頂豎向位移計算結果與誤差檢驗

從表5可知,GM(1,1)模型的最大相對誤差為16.756%,發生在預測值的終值.后驗差比值c=0.211 4,小誤差概率p=1,模型精度為Ⅰ級.GM(1,n)模型的最大相對誤差為18.874%,發生在數值擬合階段.后驗差比值c=0.435 0,小誤差概率p=0.875,模型精度為Ⅱ級.

總的來看,GM(1,1)模型的預估值和預測值與有限元計算結果的關聯度更高,GM(1,n)模型的預測效果前期不如GM(1,1)模型精度高,但預測后期精度比GM(1,1)模型更高.

3 結語

本文結合京杭運河二通道(杭州段)新開挖航段下穿滬昆高鐵工程,提供了一種基于數據挖掘的新建航道開挖及老舊航道擴建升級過程中鄰近建筑物變形演化規律的預測方法.并通過基于GM(1,1)模型的一維響應預測模型,以及基于關聯法則聯合GM(1,n)模型的多維響應模型,對不同灰色模型的預測精度進行了研究,主要結論如下:

1)基于GM(1,1)灰色模型的一維響應預測模型能較好地模擬和預測航道開挖過程中土體和結構的變形,但預測精度隨著預測個數的增加而減小,高精度預測值集中在原始序列之后的幾個值中,越往后誤差越大.

2)針對施工過程中初始階段數據較少的情況,優化的等維灰數遞補模型在小樣本數據的情況下,能顯著提高小樣本灰色模型模擬的精度,應優先使用.

3)GM(1,n)模型在擬合橋墩墩頂沉降的過程中,前期精度相比GM(1,1)模型稍低,但在后期模擬精度相比GM(1,1)模型顯著提高,實際變形預測過程中可綜合考慮GM(1,1)模型和GM(1,n)模型以提高精度,降低工程風險.