基于Dragon/Donjon 的鈉冷快堆反應性反饋參數計算與分析

張 亮，孫 勝，孫壽華，楊文華

（中國核動力研究設計院，四川 成都 610213）

為準確分析評估鈉冷快堆（Sodium-cooled Fast Reactor，SFR）堆芯性能與系統行為，分析程序的驗證與確認工作十分重要。針對SFR堆芯中子學基準題的研究與對比分析，是衡量反應堆物理計算程序與方法有效性的關鍵環節。在SFR 堆芯中子學分析方面，主要有3 大類方法：基于蒙特卡洛程序直接求解方法、基于確定論程序的兩步法以及蒙特卡洛程序制作組件群常數/堆芯程序求解方法[1,2]。第二種方法的計算效率最高，也是堆芯燃料管理的傳統方法；基于該方法開展SFR 中子學基準題的計算與分析，對于相應程序與方法的驗證具有很強的現實意義。

堆芯的反應性反饋參數，與堆芯局部的材料、溫度或幾何尺寸的變化息息相關，是反應性堆系統行為分析與事故安全分析的基礎輸入參數[3]，是用于檢驗分析程序與方法有效性的關鍵參數之一。開源的確定論中子學分析程序包Dragon[4]，包含組件計算程序Dragon 和堆芯計算程序Donjon[4]；相關文獻報道了其在SFR堆芯分析上應用情況[5,6]，但缺少堆芯反應性反饋參數相關的內容。

本文針對法國超鳳凰堆（Superphenix，SPX）的堆芯中子學基準題[7]，基于傳統的兩步法和Dragon/Donjon 程序進行堆芯計算，計算得到一系列的堆芯分區反應性反饋參數，與采用蒙特卡洛程序Serpent[8]的基準題結果[9]進行對比分析，以判斷該程序與方法在反應性反饋參數計算上的適用性與計算偏差，并分析不同的多群數據庫與堆芯計算方法對結果的影響。

1 SPX 堆芯中子學基準題

SPX 反應堆為熱功率2 990 MW 的大型鈉冷快堆，主要由190 個內區燃料組件（FAI）、168 個外區燃料組件（FAO）、225 個增殖燃料組件（RB）、294 個屏蔽組件（RS）、21 個控制棒組件（CSD）、3 個備用停堆組件（DSD）、18個稀釋組件（Diluent assembly，DL）、燃料組件上部和下部的增殖燃料區（UAB、LAB）以及氣腔段（GC）、組件進口段、組件出口段等組成[7]。SPX 的堆芯布置如圖1 所示[7]。

燃料組件采用混合氧化物燃料，增殖燃料組件采用貧化UO2，控制棒（CSD 和DSD）采用10B 富集度為90%的B4C 芯塊。堆芯組件均為六邊形組件，由三角形布置的棒束以及組件盒組成。各類組件的幾何參數、堆芯布置及其尺寸參數，材料的成分、密度、線膨脹系數等詳見基準題文獻[7,9]。

SPX 中子學基準題采用Serpent 程序建立了隨溫度變化的堆芯精細模型，并利用JEFF 3.1.1連續能量中子截面數據庫[10]開展全堆計算，堆keff計算結果的統計偏差約1 pcm[7]，文獻［9］中列出了反應性反饋參數的參考解。本文也列入其它程序對此基準題的部分計算結果：

（1）基于WIMS 程序的傳統兩步法[11]，采用輸運理論（SP3）求解堆芯，組件群常數制作基于JEFF 3.1.2 庫[10]；

（2）采用PARCS/Serpent 的蒙卡 - 確定論耦合方法[12]，組件群常數制作由Serpent 基于JEFF 3.1.1 庫制作，堆芯求解采用PARCS 程序[13]。

2 計算模型與方法

2.1 組件群常數制作

基于JEFF 3.1.1 庫和ENDF/B 8.0 庫[14]的172 群中子截面數據庫，該庫為Dragon 程序自帶，能群結構與IAEA 發布的WLUP 庫一致[15]；采用Dragon 程序建立組件的結構模型，并進行組件的均勻化群常數庫制作。核素的自屏蔽計算采用概率表表征共振截面，中子通量密度求解采用碰撞概率方法，引入超級均勻化方法（SPH）進行群參數修正。組件群常數采用24群，其中 1～20 MeV、0.1～1 MeV、0.01～0.1 MeV、1～10 keV、1 keV 以下分別有約5群、5 群、4 群、5 群和5 群；該能群結構以及最大能群上限值與文獻[5]基本相似；具體能群劃分如表1 所示。

燃料組件計算采用全反射邊界的二維單組件模型，如圖2（a）所示；芯體、氣隙、包殼以及棒柵距均詳細建模，組件盒與盒間冷卻劑則均勻打混處理。其他組件的計算采用“超柵元”模型，如圖2（b）所示，待求解組件居中，其四周圍繞著均勻打混的燃料組件。

對于不同溫度下的結構熱膨脹，包殼和組件盒的尺寸、燃料棒柵距等均考慮熱膨脹而隨溫度而改變；相應的，材料的密度隨溫度而改變，從而保證材料的總質量不變。為與基準題保持一致，MOX 芯體、增殖區的UO2芯體、B4C 芯體均只考慮一維軸向膨脹。包殼、組件盒、其他打混組件均按照相應材料的線膨脹系數進行均勻的三維膨脹，由冷卻劑填充改變尺寸后的組件盒間間隙與棒間空間；上述材料及冷卻劑的密度均隨溫度相應改變。

2.2 三維堆芯計算模型與求解方法

利用Dragon 程序包中的Donjon 堆芯計算程序建立SPX 的三維堆芯計算模型；模型中的組件布置與基準題完全一致（見圖1）；堆芯軸向上則共分為36 段，其中燃料芯體區均分為10 段，模型的縱向結構示意圖如圖3 所示。堆芯的徑向膨脹為組件柵距的均勻改變，改變后的組件柵距由堆芯入口冷卻劑溫度計算的下柵格板均勻徑向膨脹得到。對于堆芯結構的軸向膨脹，除燃料段（FA）、軸向增殖區（AB）和徑向增殖組件（RB）外，其余結構均由組件盒材料的熱膨脹決定。由于Donjon 程序只支持均勻劃分的網格，因此內區與外區的燃料段高度須保持一致，無法獨立設置不同溫度下的高度；FA 和AB 的軸向膨脹后長度可單獨制定，而RB以及RS/DL 的高度則等于FA 與AB 的高度之和。對于非均勻溫度分布的堆芯算例，此種設置由于保證了FA 與AB 質量與實際情況相同；RB、RS/DL 軸向高度與實際的細微差別對中子有效增殖系數keff的影響很小。

在堆芯中子通量密度的空間求解方法上，Donjon 可以調用擴散理論方法和不同階數的簡化球諧函數方法，并可對六邊形的組件節塊進一步進行網格剖分[16]。本文采用了兩種方法：基于擴散理論的網格中心有限差分法（MCFD）以及基于輸運理論的3 階簡化球諧函數方法（SP3）[17]；前者將六邊形節塊均勻細分為6 個三角形，后者則均分為3 個菱形網格。

2.3 反應性反饋參數的定義與計算方法

選取的基準算例為：堆芯幾何參數為673 K時的值、材料截面溫度為600 K、停堆組件DSD全提、控制棒組件CSD 自上而下插入易裂變燃料區全高度的40%（標識為CR40）。反應性參數的定義與計算方法如表2 所示。

表2 反應性反饋參數的定義與計算方法Table 2 The definition and calculation method of reactivity feedback parameters

3 計算結果與討論

3.1 堆芯徑向膨脹反應性系數

堆芯入口冷卻劑溫度從 673 K 升溫至923 K，導致堆芯下柵格板徑向膨脹，使得堆芯組件柵距增大1%；僅改變組件柵距，堆芯活性區的材料溫度與密度保持不變，相應的堆芯徑向膨脹反應性系數的計算結果如表3 所示。

表3 SPX 堆的堆芯徑向膨脹反應性系數Table 3 Reactivity coefficients of reactor radial expansion /(pcm/K)

為便于比較，所有結果均基于與基準題相同的中子核反應數據庫。由表3 可知，采用SP3算法的 Dragon/Donjon 結果與基準題的偏差為 - 0.9%，優于PARCS/Serpent 的 - 7.5%；而基于擴散理論 MCFD 算法的結果偏差較大（ - 18%）。由于SP3 方法考慮了中子注量率和散射項的角分布，可更準確的反映空間非均勻效應受幾何擾動的影響。

3.2 燃料多普勒系數

燃料或增殖燃料芯體從 600 K 升溫至1 500 K，但保持其密度與尺寸不變，得到的分區燃料多普勒系數與計算偏差如表4 所示。

表4 SPX 堆芯燃料多普勒效應的分區計算結果Table 4 The fuel Doppler constant for different core zones in SPX pcm

由表4 可知，對于內/外區燃料、全部的燃 料/增殖區，兩種庫、兩種算法的4 組Dragon/Donjon 結果均與基準題結果吻合較好；內/外燃料區域的最大偏差小于3.5%，全部的燃料/增殖燃料區最大偏差僅 1.1%，略優于 PARCS/Serpent，也與BN-600 基準題中應用兩步法[19]的偏差（1.5%）相當。對于AB 和RB，增殖燃料的多普勒系數遠小于FA 的值，且計算偏差顯著增加；MCFD 的計算偏差顯著大于SP3，而同種算法下不同庫的結果差異很小。兩種算法在增殖區的計算偏差差異，是因為擴散方法中各向同性假設在此處的局限性，而SP3 的高階角度處理則能更好的結果。

3.3 鈉密度反應性系數與鈉空泡效應

對于鈉密度反應性系數，考慮鈉從673 K升溫至1 073 K 的密度變化，而鈉空泡效應則考慮鈉由673 K 至完全氣化的密度變化時的影響；兩者的分區計算結果與偏差分別如圖3 和圖4所示。為與基準題保持一致，上述結果均只考慮組件盒內區域鈉密度的變化。

由圖4 和圖5 可知，Dragon/Donjon 基于兩種庫的計算結果基本無差異，但是SP3 的計算偏差全面小于MCFD；特別是鈉密度反應性系數/空泡效應較小的FAO 算例（2 和4）。具體的計算偏差如下：對于FAI 區域，兩種庫SP3 的計算偏差為6%～8%（鈉密度），13%～16%（鈉空泡）。FAO 區域的反應性系數的僅約為FAI的6%～11%，這是因為FAO 的中子通量密度與伴隨中子通量密度均小于FAI[20]。關于鈉空泡效應，SP3 算法的計算偏差較大，但仍小于WIMS/SP3 和PARCS/Serpent 的結果[9]。

3.4 燃料軸向膨脹反應性系數

MOX 和 UO2芯體溫度從 673 K 升至1 557 K，即軸向膨脹伸長1%；燃料芯體/增殖燃料芯體區域的長度相應增加、密度相應變化以保證質量守恒，但保持材料截面溫度不變。此算例與對應基準算例的控制棒均全提；得到的燃料軸向膨脹系數與計算偏差如圖6 所示。由圖可知，兩種庫的計算結果基本無差異；SP3的計算偏差為 - 15%；MCFD 的計算偏差較大，為 - 27%。兩者的偏差均小于 WIMS/SP3 和PARCS/Serpent[9]。

3.5 包殼與組件盒膨脹反應性系數

對于裂變燃料段包殼與組件盒熱膨脹的影響，考慮材料從673 K 升溫至1 163 K 導致的尺寸與密度變化，相應的冷卻劑體積份額隨之調整。此處只列出MCFD 算法的結果。算例1 和2 分別為FAI、FAO，且不考慮材料截面溫度效應（即材料的截面溫度仍為600 K），算例3 和4為相應區域考慮該效應的算例。包殼或組件盒膨脹反應性系數的計算結果與偏差分別如圖7和圖8 所示。

由圖7 和圖8 可知，基準解（Serpent/J311）和Dragon/Donjon/E80 的結果考慮了材料截面溫度效應，比不考慮該效應（即只有材料密度變化）的結果（正值）大為縮小。這是因為SFR中包殼或組件盒材料密度減小引入正反應性，而材料的截面溫度效應與燃料的多普勒效應類似，為負反應性效應。對于組件盒或FAO 區域包殼，這兩種效應幾乎相當，體現為圖6 中算例4 和圖7 中算例3 和4 的反應性系數幾乎為0。如圖7 中算例1 和3 所示，考慮材料截面溫度效應后FAI 區域包殼的膨脹反應性系數，比不考慮時的結果減小了約一半。因此，計算SFR中包殼和組件盒的膨脹反應性系數時，必須有效考慮材料截面溫度效應的影響。

比較算例1 和3 或者算例2 和4 的結果可知，基于ENDF/B 8.0 庫的多群中子數據庫可以準確反映材料截面溫度效應，而基于JEFF 3.1.1 庫的多群庫的結果則無法反映該效應。經分析發現，應用 Dragon 程序包自帶的基于JEFF 3.1.1 庫的多群數據庫時，組件程序對不銹鋼材料主要核素（56Fe、52Cr）調用自屏蔽計算時出錯，而使用ENDF/B 8.0 的多群庫則無上述現象。

3.6 各項反應性反饋參數的計算結果

基于Dragon/Donjon 程序得到SPX 堆的各項反應性反饋系數總結于表5。結合圖7、圖8和表5 可知，組件盒膨脹反應性系數極小，可以忽略；FAO 區域的包殼膨脹反應性系數極小，可以忽略。對于不涉及結構材料截面溫度效應的反應性系數（堆芯徑向膨脹、燃料多普勒效應、鈉密度或鈉空泡、燃料軸向膨脹產生的反應性反饋），同種算法下應用基于JEFF 3.1.1 庫和ENDF/B 8.0 庫的多群中子數據庫的結果差異很小。

表5 基于Dragon 程序的SPX 堆反應性反饋參數計算結果Table 5 Results of reactivity feedback coefficients in SPX with Dragon code

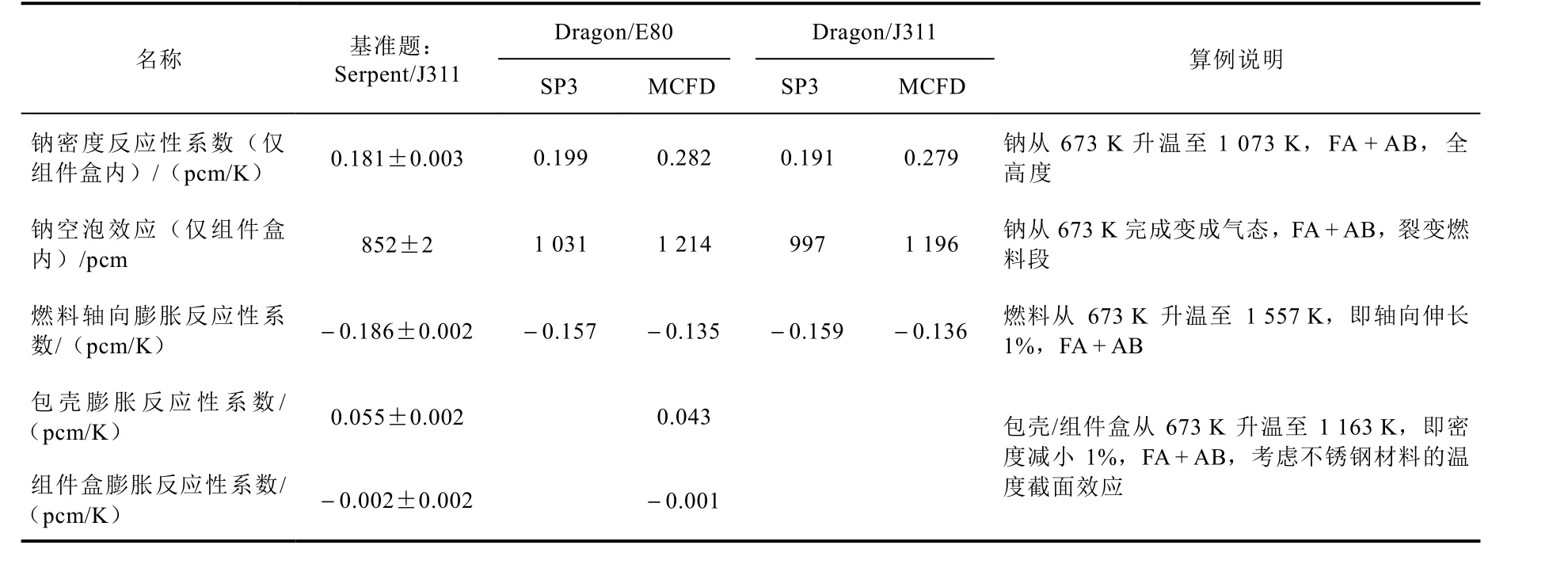
續表

4 結論

針對SPX 中子學基準題，基于傳統的兩步法和Dragon/Donjon 程序進行全堆計算，得到了一系列反應性反饋參數。相關結論如下：

（1） 與基準題結果相比，Dragon/Donjon程序得到的堆芯徑向膨脹反應性系數、燃料多普勒效應、鈉密度反應性系數、鈉空泡效應、燃料軸向膨脹反應性系數以及包殼膨脹反應性系數的計算偏差分別為0.1%～0.9%（SP3）、小于1%（SP3 和MCFD）、6%～10%（SP3）、17%～21%（SP3）、約 - 15%（SP3）和約 - 22%

（MCFD）。

（2） Dragon/Donjon 程序與基準題結果的計算偏差，與基準題中類似程序與方法的計算偏差相當；Dragon/Donjon 程序可用于SFR 堆芯的反應性反饋參數計算。

（3） 與擴算理論的MCFD 算法相比，基于輸運理論的SP3 算法可以更精確的捕捉到堆芯局部狀態變化產生的影響，對于堆芯徑向均勻膨脹、分區鈉密度變化或鈉空泡效應、燃料軸向膨脹產生的反應性反饋系數的計算偏差更小。

（4） 對于不涉及結構材料截面溫度效應的反應性系數，同種算法下應用基于JEFF 3.1.1庫和ENDF/B 8.0 庫的多群中子數據庫的結果差異很小。

致謝

本論文的工作得到國家留學基金委（CSC）的資助。